即时响应式定制公交调度优化

韩 霜，傅 惠

(1.广东工业大学土木与交通工程学院，广东 广州 510006；2.广东工业大学 机电工程学院，广东 广州 510006)

0 引言

当前公交出行需求正向个性化、品质化方向发展，国内各大城市正大力发展定制公交以满足这一需求。定制公交作为多元化公共交通的重要组成部分，是指通过集中整合个体的交通出行需求，为出行起终点、出行时间、服务需求相同或相似的人群提供专门定制的公共交通服务方式。定制公交为乘客提供“快捷、准时、舒适”的高品质公交体验，根据响应模式上的差异，可以分为静态预约式和即时响应式定制公交。目前国内已经开通的定制公交服务多属于静态预约模式，主要以通勤人员为服务对象，其面对的出行需求在时空上相对集中并且往往呈现出方向上的不均衡性。在静态预约模式中，运营企业多采用大容量公交车并根据提前征集得到的乘车需求生成线路，乘客按月、周或单次预订已开通的线路并乘车，其线路生成的提前期较长且在较长时间内保持固定，车辆运行途中一般不进行路线调整。即时响应式定制公交既可为通勤人员也可为临时出行者提供服务，它多采用中小容量公交车，通过实时信息交换系统整合接收到的乘车请求，综合考虑车辆行驶中的多种限制条件，迅速规划并开行定制公交线路，系统在车辆行驶过程中持续接收新的乘车请求并判断可响应的请求，然后调整行车路线并实时调度车辆完成被响应乘客的运送。即时响应式定制公交具有较大的灵活性和广泛的适应性，对私家车出行者具有较大的吸引力，有利于充分发挥定制公交在替代私家车出行、缓解拥堵和降噪减排等方面的积极作用。

定制公交属于需求响应式公交，对于需求响应式公交系统的理论研究可以追溯到20世纪60年代末[1]。Nourbakhsh等对无固定路线和站点的需求响应式公交系统进行了研究，在理想化的正方形城市中，以运营和乘客成本最小为目标，探讨了线网最优布局、车辆最优服务区域和发车间隔[2]。Bakas等研究了带时间窗并且具有固定车队规模情况下的需求响应式公交系统的调度方法[3]。Kim等分析了乘客需求对传统公交与需求响应式公交系统最优性的影响，对两种公交系统的车辆规格、发车间隔和车队规模，传统公交的线路间距以及柔性公交的服务区域进行了优化[4]。Boyer等基于司机休息时间、连续工作时间、加班时间等限制条件研究了灵活公交系统的车辆及司机调度方案[5]。近年来，专门针对定制公交的研究开始兴起，主要集中在定制公交的评价[6]、票价制度[7]及线网规划[8-12]等方面。为提高定制公交线路的适应性，王健等根据前1天乘客向公交企业提交的出行需求优化第2天定制公交车辆的调度[13]。针对动态出行需求，Bruni等考虑车辆运行过程中需求的变化，提出了需求响应式公交系统的鲁棒优化，在前期线路规划中同时考虑已知需求及后续未知需求可能引起的路线偏离的影响，减少车辆的绕行成本[14]。邱丰等研究了可变线路式公交的调度，将实时需求插入到根据预约需求规划的行车计划中[15]。郭晓俊针对多起点单终点的定制公交线路，分别建立了发车前根据预约需求进行线路规划、发车后对线路周边实时需求进行响应的优化模型[16]。

综上所述，目前对即时响应模式下的定制公交调度研究比较少，并且针对动态需求的相关研究大多直接采用实时需求进行车辆调度决策。由于单次提交的乘车需求随机性较大，以此为依据进行的调度难以实现系统整体最优，同时也可能出现线路数量和线路行车方向波动较大的情形，影响公交系统的稳定运营，也增加了运营企业在运营资源管理上的复杂度。鉴于此，针对即时响应模式下的定制调度，本研究采用两阶段优化模型对其调度进行优化：首先根据区域内分时段的高概率出行OD点对(可根据历史乘车需求提取出或通过交通大数据分析提取)的地理分布，从整体上对定制公交车辆的初始线路进行优化；其次，以初始线路为基础、根据实时乘车请求对车辆的行驶路线和停靠时间等进行灵活调度，以实现车辆对实时出行请求的及时响应。该两阶段调度方法的优势在于：(1)根据分时段的高概率出行点对定制公交车辆的初始线路进行整体优化，在减少营运车辆(线路)的同时维持高覆盖率；(2)以初始线路为基础并根据实时出行需求对车辆进行调度，综合考虑了实时出行需求以及出行规律对定制公交车辆调度决策的影响，有利于提高车辆与乘客的匹配率，增加服务的乘客数量并提高服务水平。

1 即时响应式定制公交调度决策过程

即时响应式定制公交调度决策是行驶线路预规划与车辆实时调度的综合体。由于即时响应式定制公交需要整合高度分散和随机的乘客出行需求，基于提高定制公交系统效益和服务水平的考虑，本研究提出在调度中首先根据区域内分时段的高概率出行OD点对(如商业中心、大型社区等)预先优化定制公交车辆的初始路线；当某条线路接收到的实时出行请求达到一定数量时，则启动该线路的运营，以初始线路为基础，根据可响应的实时出行请求调整车辆行驶路径并调度车辆按照决策的时间点运送乘客。即时响应式定制公交调度决策过程如图1所示。

图1 即时响应式定制公交调度决策过程Fig.1 Decision procedure of real-time responsive customized bus dispatch

在车辆初始线路规划阶段，根据区域内分时段的高概率出行点的地理位置、OD关系以及上/下车站点顺序预先规划车辆初始线路，对该时段内需要的定制公交车辆数量(线路数量)、车辆初始经停站点和停靠顺序等进行决策。车辆初始线路规划有利于运输企业以最少的车辆(线路)覆盖服务区域内的主要出行点，提高运营线路与出行需求的适应度。在车辆实时调度阶段，以初始线路作为参考路径，可选择初始线路中的全部或部分站点作为车辆行驶过程中的必经站点；在此基础上，结合实时乘车请求的时间和空间分布、上/下车站点关系、上/下车时间点、车辆容量等限制条件进行序贯决策，判断是否能够将某个乘车请求加入到行车计划中；最后，根据可响应的乘车请求调整车辆行驶路径并调度车辆按决策的到站时间运送乘客。在定制公交调度中，往往需要平衡运输企业的经济效益(利润或运营成本)和乘客出行品质(服务水平)。

上述两阶段调度方法，从整体(全区域车辆规划)和局部(单车调度)两个层面去平衡运输企业和乘客利益，既保持了即时响应式定制公交的灵活性，也使得其线路方案能够在时空维度上整体把握需求规律，有利于定制公交系统以较少的线路覆盖区域内的主要出行需求，并且其调度方案兼顾了实时需求与后续最可能需求，规避了仅依靠实时需求进行决策带来的弊端。

2 即时响应式定制公交调度优化建模

2.1 问题描述

本研究的即时响应式定制公交调度可以描述为：乘客通过实时信息交换平台提交上/下车站点、上/下车时间点(即服务的时间窗)及乘车人数等乘车请求；定制公交系统根据实际限制条件分析得出可以响应的乘车请求，允许车辆晚于乘客要求的上/下车时间点到达，但晚于下车时间到达将产生延误成本；定制公交系统信息平台向乘客反馈决策结果，然后按照决策获得的时间和地点调整车辆的行驶路线，调度车辆及时运送乘客。

为便于建模，做出如下假设：

(1)乘客均通过定制公交信息平台提交乘车请求，包括上/下车位置、上/下车时间点和乘车人数。

(2)各个站点都仅有一个上车或下车请求，若一个站点同时具有多个上车或下车请求，在模型中将其拆分为地理位置相同的多个站点。

(3)任意站点间的行驶距离已知，站点间的距离为路网中各站点间的最短行驶距离。

(4)除车辆启动和停车阶段外，定制公交车辆以匀速行驶。

(5)定制公交票价为按次收费的均价。

2.2 车辆初始线路优化模型

为方便模型的表达，定义集合及参数如下：N为规划区域内分时段的高概率出行点集合，N={1,…,n1}，N=N+∪N-，N+为上车点集合，N-为下车点集合；{0}为车辆的虚拟车场；L为定制公交车辆集合，L={1,…,l1}；dij为路网中站点i与站点j之间的最短行驶距离；dmax为定制公交车辆初始线路的最大长度限值；M为每辆车初始线路中的最大站点数；alij为0-1变量，车辆l从站点i开往站点j时取值为1，否则取值为0。

定制公交车辆初始线路优化模型如下：

minZ1=|L|，

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

alij∈{0, 1}， ∀l∈L,i∈N,j∈N，

(8)

公式(1)表示定制公交系统的运营车辆数量最小，|L|为集合L中元素的个数；公式(2)表示定制公交车辆的初始行驶距离不超过最大值；公式(3)表示每个高概率出行点都必须被定制公交车辆覆盖；公式(4)表示驶入与驶离中间站点的定制公交车辆数量相等；公式(5)和公式(6)表示车辆需要从虚拟车场出发并且最终回到虚拟车场，公式(7)表示除虚拟车场外，车辆经停的初始站点数量不超过M；公式(8)是决策变量的取值约束。

2.3 车辆实时调度决策模型

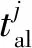
定制公交车辆实时调度决策模型如下：

(9)

(10)

(11)

s.t.

(12)

(13)

(14)

∀j∈Nm+∪Ns+,F(j)∈Nm-∪Ns-,

(15)

tj+2ts+tjF(j)≤tF(j), ∀j∈Nm+∪Ns+,

F(j)∈Nm-∪Ns-，

(16)

(17)

(18)

(19)

xij∈{0, 1}， ∀i,j∈Nm∪Ns。

(20)

公式(9)表示使定制公交车辆晚于乘客要求的时间送达造成的延误成本最小；公式(10)表示定制公交车辆的利润最大化；公式(11)表示因未响应乘客而导致的惩罚成本最小；公式(12)表示车辆必须访问必经站点；公式(13)表示车辆可以访问或者不访问可选站点；公式(14)表示车辆访问中间站点以后必须离开；公式(15)表示定制公交车辆若访问了上车站点j，则必须访问其对应的下车站点，F(j)为上车站点j对应的下车站点；公式(16)表示车辆必须先访问上车站点才能访问其对应的下车站点；公式(17)表示车辆在车乘客总数不超过车辆最大载客量；公式(18)和(19)表示车辆从虚拟车场驶出并最终回到虚拟车场；公式(20)为决策变量的取值约束。

3 模型求解算法

3.1 车辆初始线路优化模型的遗传算法设计

定制公交车辆初始线路优化模型是一个线性整数规划模型，本文采用遗传算法进行求解。遗传算法的主体框架与基本遗传算法类似，故在此仅对遗传算法的编码、初始种群以及遗传算子进行简要说明。

(1)编码

定制公交车辆的初始线路是由多个站点按照一定顺序排列形成的序列，本文采用自然数1，2，…，m表示服务区域内的高概率上车站点，其对应的下车站点则采用m+1，m+2，…，2m进行编号。在遗传算法中，染色体采用实数编码并用二维矩阵存储，矩阵的每一行代表一辆车的初始线路，如图2所示。

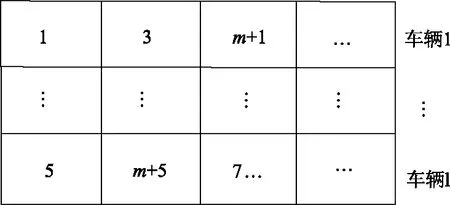
图2 车辆初始线路优化模型的编码Fig.2 Coding of vehicle initial route optimization model

(2)初始种群

初始种群的质量将影响遗传算法的搜索效率，为提高初始种群中的染色体质量并保证种群多样性，采用以下方法生成初始种群中的染色体：

① 随机扰乱高概率出行点对的排列顺序；

② 选择第一对高概率出行点，构成第1辆车的第一对经停站点；

③ 选择下一对高概率出行点，以插入后行驶距离增加值最小为原则将其插入第l(l=1,2,…,l1) 辆车的经停路径，判断是否满足所有约束，如果满足则调整该车辆的初始路径，否则将该高概率出行点对插入下一辆车的经停路径, 不断重复上述过程，直至找到满足约束的最佳插入位置；

④ 依次选择余下的高概率出行点对，重复步骤③，直至将所有高概率出行点对都插入车辆的初始路径中。

(3)交叉算子

为了加强遗传算法的全局搜索性能，扩大算法的搜索范围，交叉算子采用整条路径交换的形式：首先随机选取两个父代染色体，随机在两个父代染色体中各选一条车辆初始路径，然后进行交换；最后对子代染色体进行修整，使得子代染色体满足约束条件。

(4)变异算子

变异算子主要用于小范围调整站点顺序：首先随机挑选出进行变异的父代染色体，然后在该染色体中随机选择一对高概率出行点作为变异点，将该高概率出行点对重新插入其他车辆的路径，并对变异后的子代染色体进行修整，以保证染色体满足约束条件。

3.2 车辆实时调度决策模型的NSGA-II算法设计

定制公交车辆实时调度决策模型是一个多目标的非线性整数规划模型，采用带精英策略的快速非支配排序遗传算法(NSGA-II)进行求解。本研究NSGA-II算法的基本框架以及快速非支配排序、虚拟适应度计算以及精英保留策略与文献[17]～[18]相似，以下仅对编码和遗传算子进行简要说明。

(1)编码

车辆实时调度形成的最终行驶路径是由已确定的必经站点和新一轮决策中加入的可响应站点组成的序列。在每一轮优化中，都只需确定乘客新提交的乘车请求中哪些乘车请求可以被响应，即哪些OD对能够加入到原有的行车计划中。采用二进制编码对车辆实时调度决策模型的染色体进行编码，1代表相应的OD对被响应，0则反之。

(2)遗传算子

车辆实时调度模型的交叉算子为二进制编码规则下的两点交叉，变异算子为二进制编码规则下的单点变异。

4 案例分析

选取广州市内的50个高概率出行点(主要为学校、住宅小区、商业设施、公共服务设施等)及其OD关系进行实时响应式定制公交调度决策的模拟， OD点对及经纬度如表1所示。

各出行点间的路网最短距离采用百度API计算获得。车辆初始线路优化模型的参数设置如下：车辆初始线路径长度不超过35 km，初始站点数量不超过12个。通过试算，确定遗传算法参数如下：种群规模为50，交叉概率0.6，变异概率为0.4，进化代数为500。经过计算，需要6辆车(6条线路)覆盖所有的高概率出行点， 每条线路的经停站点如表2所示。

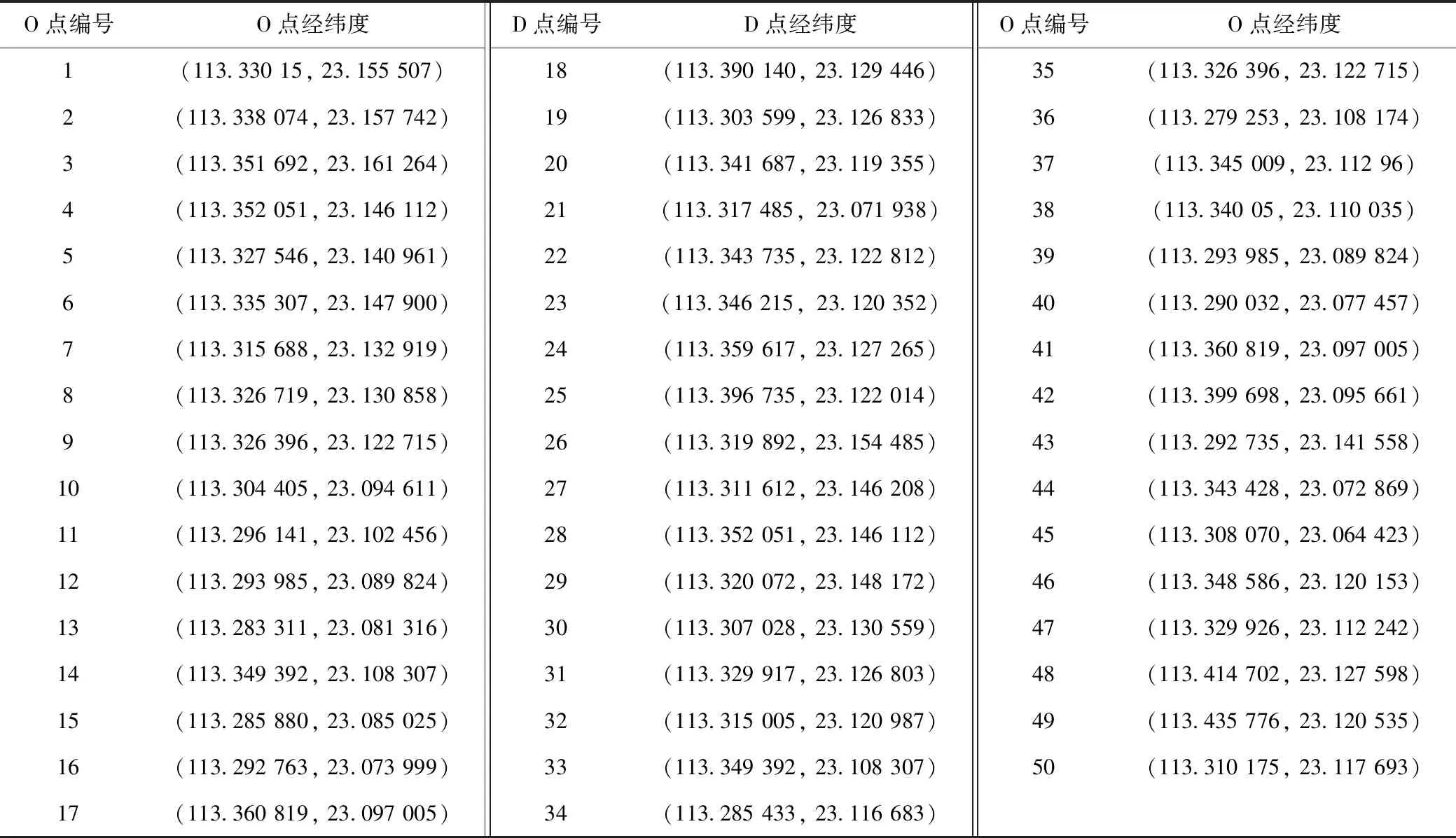
表1 高概率出行OD点对Tab.1 OD pairs in high-probability travel

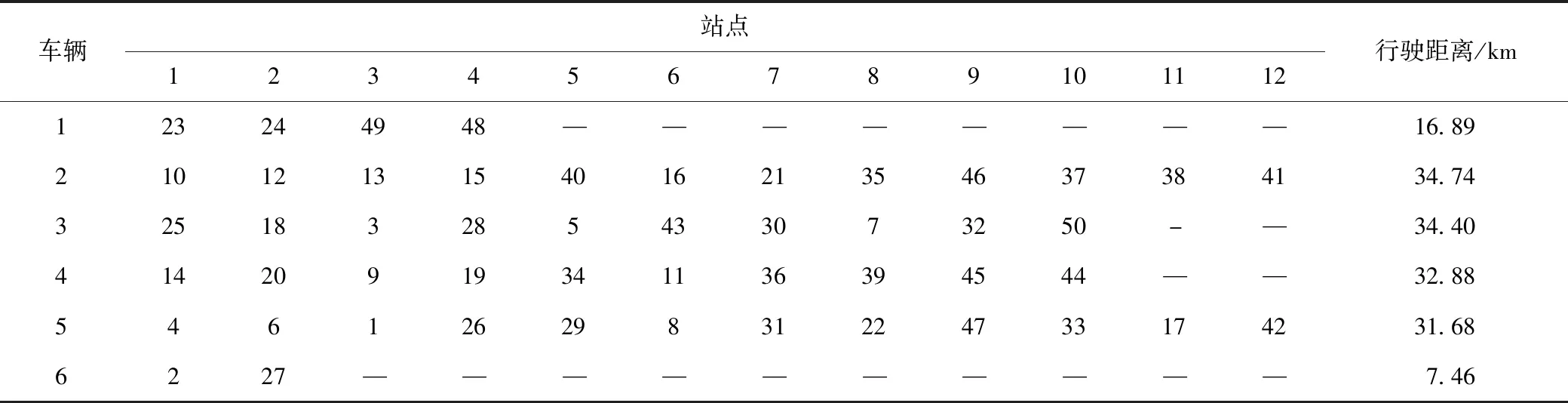
表2 车辆的初始路径方案Tab.2 Scheme of vehicles’ initial routes

当线路接收到一定数量的出行请求时，该线路即开始运营，其车辆的调度决策基于站点进行序贯更新。因篇幅有限，本研究仅列出车辆5(线路5)的实时调度结果。模型中相关参数设定如下：车辆行驶速度为35 km/h，车辆启/停时间为2 s/次，车辆有效座位数为26，车辆变动成本为80元/时，固定成本折合到单位车时为40元；每个乘客上/下车时间为1 s/人；σ1为5 000，σ2为200；票价为10元/次。NSGA-II算法参数如下：种群规模为20，迭代次数为100，交叉概率0.9，变异概率为0.1。随机产生3批乘车请求，如表3所示。为方便计算，将车辆5初始线路中的实际经停站点按照访问顺序重新用1-12编号，实时响应的乘车请求从13开始依次编号，奇数为上车点，偶数为下车点。经计算，车辆5的路线调整方案如表4所示，车辆到达各个站点的时间如图3所示(单位：分)。进一步对数据进行分析可知：车辆5共搭载乘客29人，未响应乘客数为17人；由于在响应时间上采用柔性匹配，车辆在部分站点出现送达延误，最大延误发生在站点24，延误时间为12.6 min，平均延误时间为5.2 min，在非紧急出行中，该延误在可接受范围之内。案例分析的结果说明采用所提出的两阶段调度方法能够取得较好的调度效果。

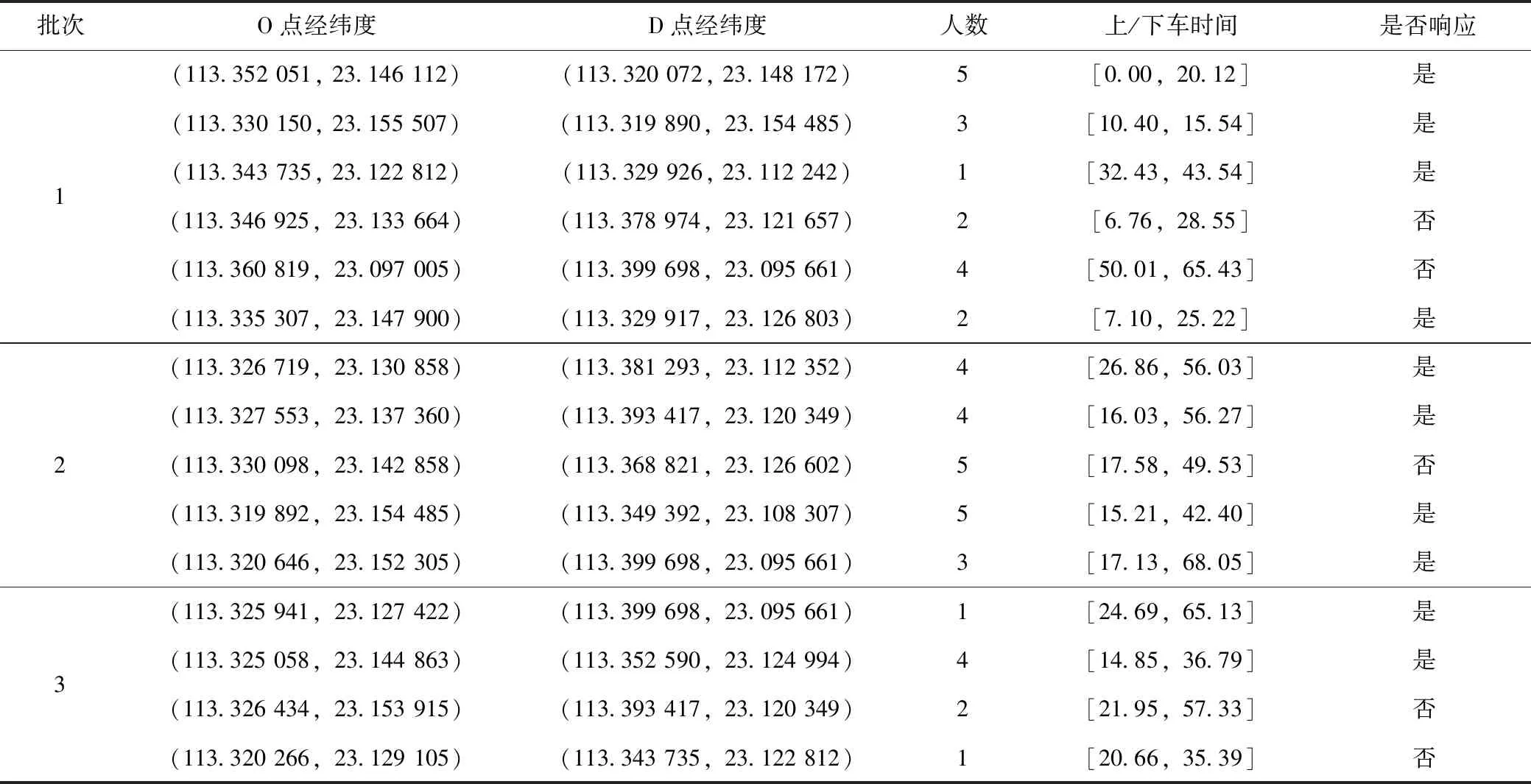
表3 车辆5的实时乘车请求Tab.3 Real-time riding requests of vehicle 5

表4 车辆5的线路调整方案Tab.4 Route adjustment scheme of vehicle 5

注：圆括号内的数字表示编号不同但地理位置相同的站点。

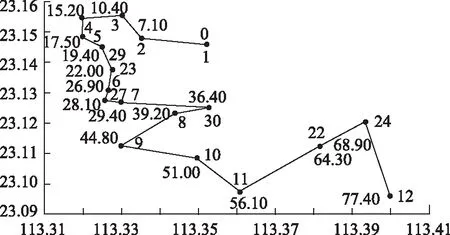
图3 车辆5到达站点的时间(单位:分钟)Fig.3 Arrival time of vehicle 5(unit:min)

5 结论

调度是影响即时响应式定制公交运营的关键技术，本研究兼顾运输企业和乘客利益，综合考虑定制公交出行需求规律及实时出行请求对调度决策的影响，建立了即时响应式定制公交两阶段调度模型，即初始线路优化模型和车辆实时调度决策模型：首先以运营车辆数最小为目标对定制公交系统的初始线路进行整体优化。在此基础上根据实时出行请求，以乘客延误成本最小、运输企业利润最大以及未服务乘客造成的损失最小为目标进行车辆实时调度。该方法具有以下特点：以较少的车辆(线路)覆盖区域内的主要出行点；同时考虑实时出行请求以及需求规律对车辆进行实时调度，调度方案既满足了当前的实时需求也兼顾了后续最可能出现的出行需求，提高车辆与出行需求的匹配率。根据模型的特点，分别设计了求解模型的遗传算法和NSGA-II算法。最后，选取广州市内的部分高概率出行点进行了案例分析，计算结果表明本文提出的两阶段调度模型以及设计的算法能够提供合理的实时调度方案。即时响应式定制公交调度是一个复杂的技术问题，本文的车辆实时调度决策模型仅针对各线路进行单独的调度决策，没有考虑线路交叉情况下的乘客需求响应问题，并且在调度中也未能考虑车辆行驶速度的动态性，这将是下一步研究的方向。