主应力轴旋转条件下饱和粉质黏土应变特性及非共轴性的试验研究
2020-06-19张树光刘文博赵海智孙博一
张树光,陈 雷,刘文博,赵海智,孙博一
(1.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000;2.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;3.广西岩土力学与工程重点实验室,广西 桂林 541004)
0 引言
土属于压硬性材料,在自然界或者工程中往往表现出各向异性的特征。在经历波浪、交通、地震荷载等复杂的应力条件作用时,土体单元受到主应力的大小不仅会发生改变,主应力方向角也会发生改变。在公路上车轮的移动便会对路基土单元所受主应力的方向角产生影响[1-2]。随着荷载的不断循环,主应力轴会发生循环往复的变化。针对主应力轴发生偏转的土体试样,利用常规试验器材在研究其强度变化、应力应变曲线及其孔压特性时,往往不能模拟主应力轴旋转而与实际工程中土体的受力情况相差甚远,导致了传统土体本构模型和理论不能满足工程需求[3-4]。其中,主应力轴旋转是指在复杂应力条件下主应力方向与竖直方向夹角发生改变。在岩土工程中,土体在交通荷载、地震荷载及波浪荷载的连续作用下,会导致地基基础、基坑边坡及堤坝等工程因受到外部荷载而使内部土体发生主应力轴连续循环旋转问题[5]。
国内外学者针对不同中主应力系数和偏应力影响下和主应力轴旋转条件下,饱和粉质黏土非共轴性及对非共轴角随主应力轴旋转角之间关系的研究较少,但在主应力轴旋转条件下对土体的强度特性、孔压特性、变形特性及非共轴特性等方面的工作取得了丰硕的成果。其中,Ishihara等[6]利用GDS空心圆柱扭剪仪以砂土为研究对象进行了主应力轴循环旋转试验,以剪应力为确定条件,进行了砂土动力特性测试。Symes 等[7]、Miura等[8]、Nakata等[9]在主应力轴纯旋转试验过程中保持平均主应力、广义偏应力和中主应力系数3个控制参数恒定,证明了主应力轴方向角的变化能使土体发生应变软化,进而发生破坏。Lade等[10]进行了一系列大尺寸的空心圆柱试样的循环扭剪试验,研究了主应力轴旋转和中主应力比对淤泥土应力应变曲线发展规律、孔压特性和强度特性的影响。沈杨[11]利用空心圆柱扭剪仪以软黏土为研究对象,进行了一系列不同主应力轴方向变化应力路径下的试验。沈杨等[12]应用空心圆柱循环扭剪试验,得到了主应力轴定向剪切和主应力轴旋转两种条件下软土非共轴应变特征的变化规律。蔡燕燕等[13-14]进行了偏应力不变主应力轴旋转及改变偏应力同时旋转主应力轴两种应力路径条件下的砂土排水试验。赵彦虎[15]针对主应力轴旋转对土体变形的影响,以重塑黄土为研究对象进行了不同应力路径下的扭剪试验,验证了土体剪切强度与中主应力系数和主应力旋转角有密切联系,证明了主应力轴旋转使得土体的塑性应变不断积累。上述研究对于土样的非共轴性研究对象大多是砂土,而在南方建筑工程中所遇到的工程土体大多数为黏土,黏土的性质较砂土在复杂地质环境中多变,且黏土的非共轴变形对工程的开展具有较大影响,故需要对复杂应力路径下黏土的非共轴变形及影响土体非共轴性的因素进行深入研究。
本研究利用美国GCTS公司HTC-100电液伺服动态空心圆柱扭剪仪对空心圆柱饱和粉质黏土试样进行纯主应力轴旋转的扭剪试验,获得饱和粉质黏土试样在该应力路径下轴向应变、径向应变、环向应变及剪切应变随主应力轴旋转角的变化趋势,研究应力方向与应变增量方向的非共轴变化特征,验证剪正应力比与剪应力呈双曲线变化规律。
1 试验方案及试样受力分析
1.1 试验设备
本试验采用美国某公司HTC-100电液伺服动态空心圆柱扭剪仪。该仪器实物图见图1(a),其主要组成部分包括:(1)内外围压及其反压控制加载系统;(2)轴力、扭矩驱动力系统和压力室;(3)数据采集及其控制系统;(4)计算机控制系统。空心圆柱试样见图1(b)。

图1 试验设备及试样Fig.1 Test equipment and sample
空心圆柱加载时受力如图2所示。
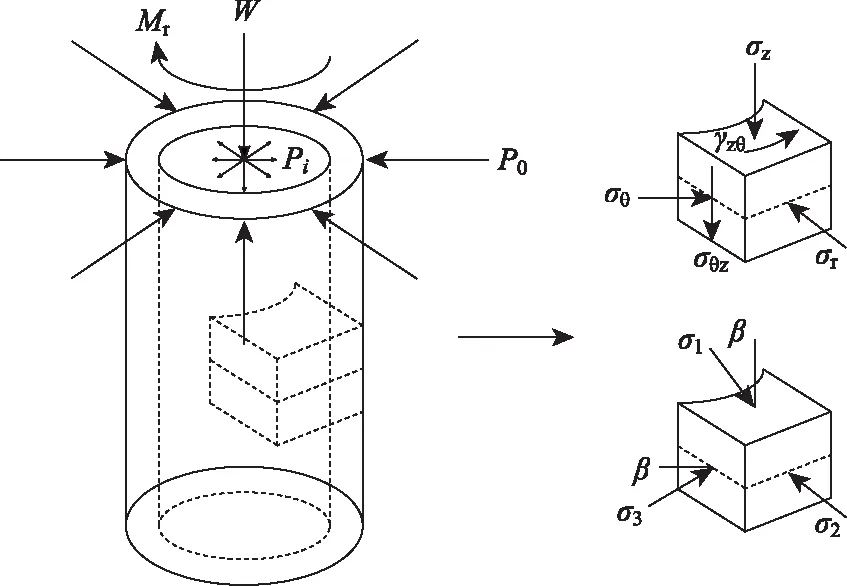
W—轴力;Mr—扭矩;Pi—土样的内压;P0—外压;σz—单元体上轴向应力;σr—径向应力;σθ—环向应力;γzθ—扭剪应力;σθz—剪切应力;σ1—第1主应力;σ2—第2主应力;σ3—第3主应力;β—第1主应力方向与垂直方向的夹角及第3主应力方向与水平方向的共轴角。图2 空心圆柱试样受力图Fig.2 Force diagram of hollow cylinder specimen
1.2 饱和粉质黏土试样物理试验及试样制作
试验饱和粉质黏土土样取自武汉11号地铁开挖基坑内。取土深度距地面2 m,先搭设工作平台,然后进行人工取土。取土前,将原取土面上的浮土进行清理,采用取土器进行取土,取得的土样用塑料薄膜包裹放到特定容器内带回实验室。对土样物理性质的测定数据见表1。
在制作重塑试样时,可将取回的土试样进行切分放入烘干箱,在150 ℃温度下烘干24 h,随后将烘干后的土样进行粉碎并将粉碎土试样经过0.15 mm 的细孔筛分,加入无气水按最优含水率作成土样,放入密闭桶里放置24 h,然后将泥块取出利用击实桶击实。将制备好的试样用保鲜膜包裹放入密封箱中保存,将制作好的实心试件放在ZK-270型真空饱和缸里进行抽气,直到缸内负压达到30 kPa时保压40 min,随后打开进水阀门在大气压的作用下注入清水进行真空饱和固结。最后将固结完成的重塑土试样放置于特制的空心圆柱试样的切土器上,用专用的空心圆柱试样内心切割器钻取直径=60 mm的空心,制成的空心圆柱试样如图1(b)所示,尺寸为外径直径100 mm,空心直径60 mm,高度200 mm。

表1 试验土样物理性质指标Tab.1 Physical properties of soil sample for test
1.3 试样饱和与固结
对空心圆柱饱和粉质黏土试样采用3级反压饱和的方法进行饱和处理,具体操作步骤及其控制数据如下:对试样同时施加20 kPa的初始内外围压,随后以内外围压差30 kPa的递增速率对试样施加内外围压,反压值设定为50 kPa,轴向力设定为0.05 kN;将目标围压设定在50 kPa,反压增至100 kPa;将目标围压设定在80 kPa,反压增至150 kPa。
在设定以上参数的同时,要勾选最大试验时间及自动进入下一步试验选项,这样可以定时进行下一步的操作过程。当该空心圆柱饱和粉质黏土试样的孔压系数B≥0.98时认为试样达到饱和。通常情况下,该饱和过程持续时间约为24 h。某组反压饱和曲线如图3所示。当饱和完成后,采用排水固结法对试样进行各向同性的固结。固结过程中,施加一定的应力达到所需的初始有效应力状态。设置相等的内外围压,使得有效围压为150 kPa,在此条件下对试样进行固结。当试样的排水量小于100 mm3时,认为试样固结完成(图4),随后进行加载试验阶段。
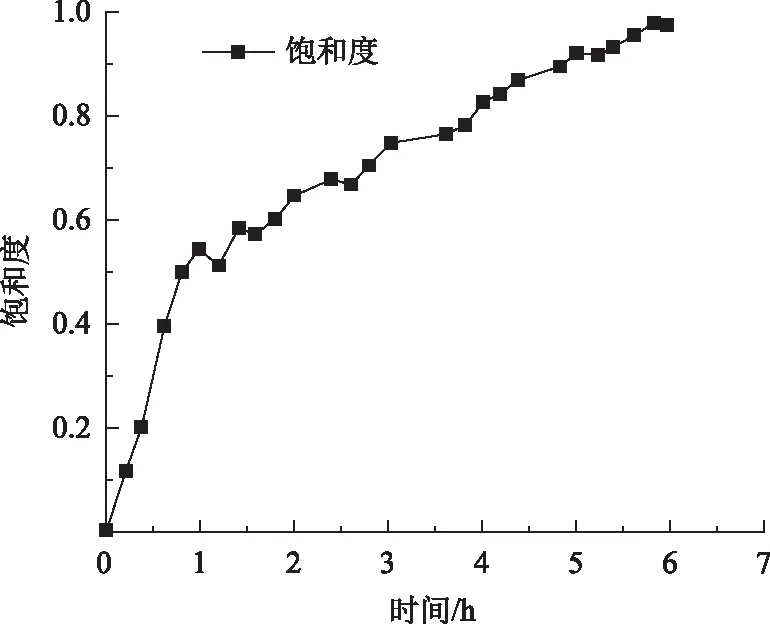
图3 试件反压饱和曲线Fig.3 Back-pressure saturation curve of sample
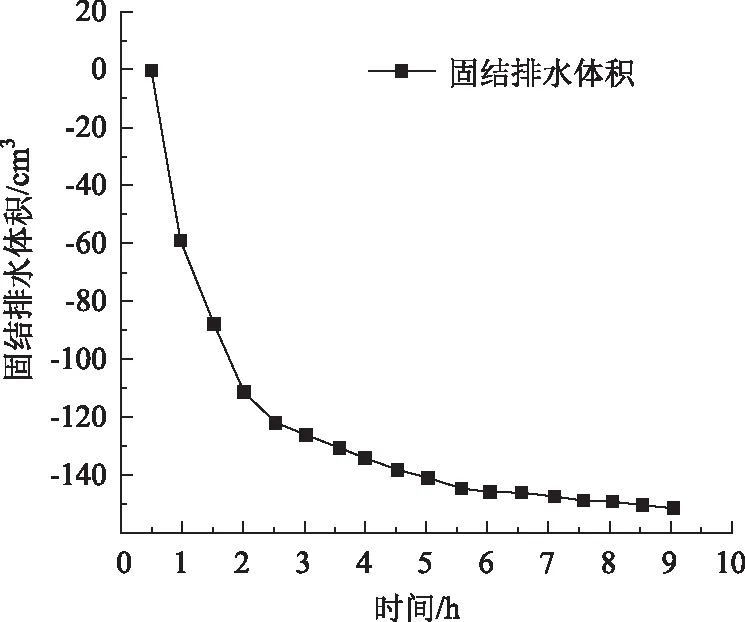
图4 试件固结排水体积曲线Fig.4 Consolidation drainage volume curve of sample
1.4 饱和粉质黏土主应力轴纯旋转试验方案
为了研究在主应力轴纯旋转条件下饱和粉质黏土的应力-应变变化规律及应力应变非共轴特性,将平均应力大小设置为150 kPa,且设置在中主应力系数b=0.5条件下的偏应力q值为25,35,45,55 kPa,以研究不同q值的大小对试件的影响效果。同时加设两组q值为35 kPa,b=0,b=0.75和b=1的对比试验,以研究中主应力系数对空心圆柱饱和粉质黏土试样的影响效果。在加载过程中,主应力轴旋转速率设定为30 °/h,主应力轴旋转角α变化范围为0°~180°,具体试验方案如表2所示。根据该试验方案,在(σz-σθ)/2~γzθ坐标系中绘制试验应力路径与主应力轴旋转角的关系,如图5所示。
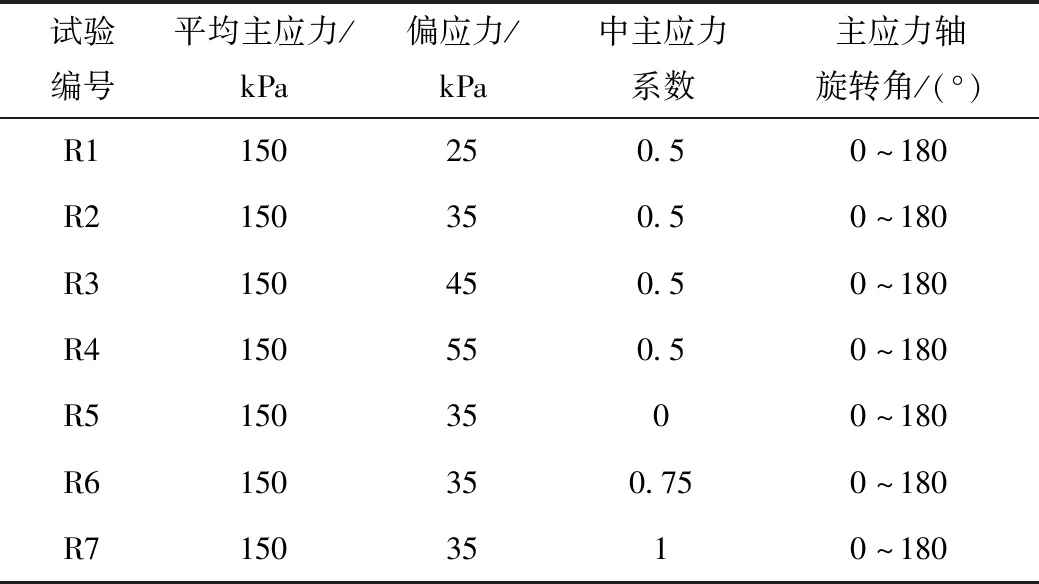
表2 主应力轴纯旋转试验方案Tab.2 Test scheme of principal stress axis purely rotation

α—主应力旋转角;τzθ—空心圆柱试样剪切应力;σz—轴向应力;σθ—轴向应力图5 主应力轴旋转角与试验应力路径关系Fig.5 Relationship between rotation angle of principal stress axis and test stress path
2 主应力轴纯旋转作用下饱和粉质黏土的应变特征
2.1 不同偏应力对土样应变特性的影响
在主应力轴旋转条件下,不同的偏应力q值在加载过程中会对饱和粉质黏土试样内部的各个主应力分量产生不同的影响,这样便会使得饱和粉质黏土试样的变形特征有不同的变化趋势。通过试验数据的分析对比,得到了不同q值下饱和粉质黏土试样的轴向应变εz、径向应变εr、环向应变εθ和剪切应变γzθ随主应力轴旋转角的变化曲线。现对主应力轴旋转两周时土样的应变趋势做如下分析。
由图6可知,试验开始阶段,不同q值下的轴向应变都为0。随着主应力轴旋转角α的增加,轴向应变值不断积累,且q值越大,轴向应变的速率发展越迅速;q为25,35,45 kPa的应变曲线大部分位于0值以下,但是有少许部分为正值,在循环加载过程中轴向应变表现出拉伸-压缩交替的现象,且q越大,试件的拉伸状态越明显;但当q增加到55 kPa,应变曲线整体位于负值方向,说明试样的轴向应变始终表现为拉伸状态;当q为25,35,45 kPa 时,3者在波峰波谷处的值接近等差变化趋势;当q继续增大变为55 kPa时,变形量相差变大,说明在此偏应力下,土体的应变软化性能加强,接近饱和粉质黏土试样的极限值。同时,试样轴向应变波峰、波谷处的α会滞后于轴向应变峰值点处的α约20°,这种滞后性是由应力方向与应变增量方向非共轴引起的。

图6 不同偏应力下轴向应变曲线Fig. 6 Axial strain curves under different deviatoric stresses
由图7可知,环向应变随着主应力轴旋转角的增大而呈现波浪式曲线变化。从数值上看,除了试验开始阶段应变值为0外,q为45,55 kPa的环向应变自始至终均为正值,说明饱和粉质黏土试样在环向方向上正处于压缩状态;而q为25,35 kPa时,试件表现为拉伸-压缩周期性的更替特征;随着q值的逐渐增大,环向应变的波动幅度也随着增大,应变速率发展也越迅速;主应力轴旋转到第2圈,各个q值下的环向应变出现了明显的塑性应变增量;在主应力轴旋转角到180°时,q为25,35 kPa的应变曲线相交于0值以下,表现出微量的拉伸状态,而q为45,55 kPa的应变曲线相交于0值以上,且有部分曲线重合。
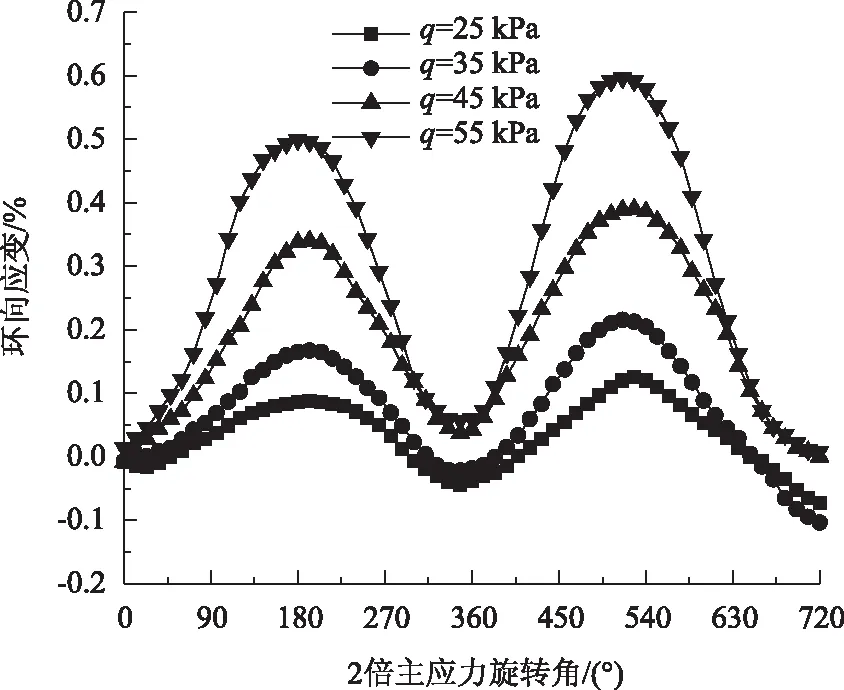
图7 不同偏应力下环向应变曲线Fig.7 Hoop strain curves under different deviatoric stresses

图8 不同偏应力下径向应变发展曲线Fig.8 Radial strain curves under different deviatoric stresses
由图8可知,饱和粉质黏土试样的径向应变呈现出接近直线的变化趋势。q为25 kPa时,径向应变为负值,表现出拉伸特性;q值为55 kPa时,径向应变为压缩变形,处于两者间的偏应力总体变形不是很明显,位于从拉伸变形转化为压缩变形的过渡区域。
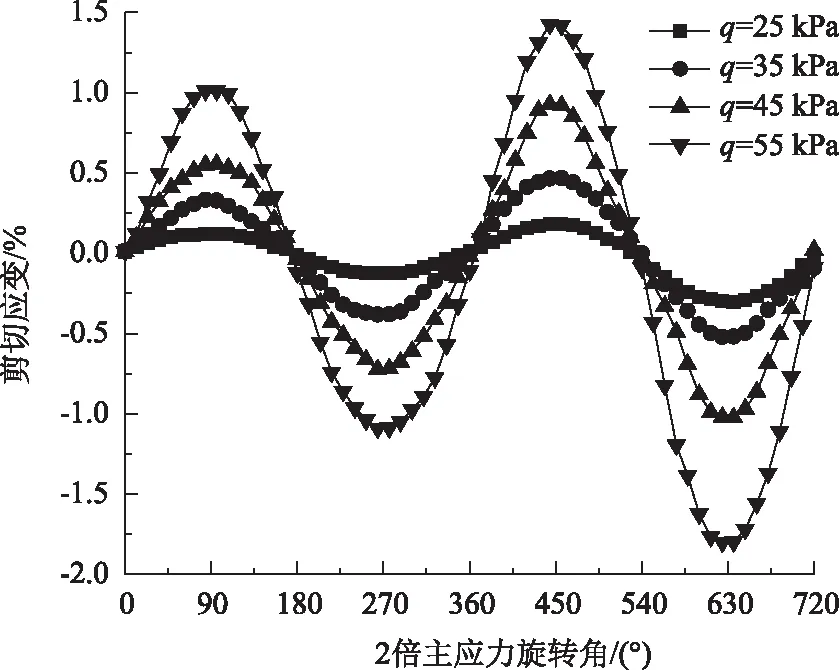
图9 不同偏应力下剪切应变发展曲线Fig.9 Shear strain curves under different deviatoric stresses
由图9可知,q值越大,剪切应变速率发展越迅速。当q为25 kPa时,曲线波动变化不大,在前期接近于水平线;当q增加时,曲线周期性的波浪形走势有明显波动,当q增至55 kPa时,同一旋转角下的峰值成倍增长。以γzθ=0为对称轴,q值越大,剪切变形曲线的对称特性表现就越明显。不同于其他几个应变值的变化趋势,各个偏应力的剪切应变随着α的变化而发生压缩、拉伸循环出现的现象。综上所述,随着剪应力的增大,空心圆柱饱和粉质黏土试样的变形越明显,应变速率就越迅速,随着α的变化,各个应变曲线走势呈现类似正弦函数曲线的波浪式变化。
2.2 不同中主应力系数b值对土试样应变特性的影响
以中主应力系数b为控制条件,分析在此条件下空心圆柱饱和粉质黏土试样随着α变化的变形特性。
空心圆柱饱和粉质黏土试样在主应力轴纯旋转的应力路径作用下,试样中的第1主应力和第3主应力在其组成的平面内做旋转运动,第2主应力的大小和方向不发生改变,但改变包含第2主应力的参量——中主应力系数b时,也会对试样的变形特性产生不容忽视的影响。下面分别对不同中主应力系数下试样的轴向应变、径向应变、环向应变和剪切应变进行分析。
由图10可知,不同中主应力系数b对试样的轴向应变形响较为显著。b=0,b=0.5和b=0.75条件下,试样的变形主要表现为沿着轴向应变εz=0的轴线做循环拉伸-压缩的波浪式运动,当b=1时,轴向应变整体为负值,表现出明显的拉伸变形。b越大,随着α的增大,变形发展越迅速,试件的拉伸特性越明显;在主应力角旋转到180°后,应变发展速率大幅度提升,各个中主应力系数下的变形有明显的塑性应变增量。
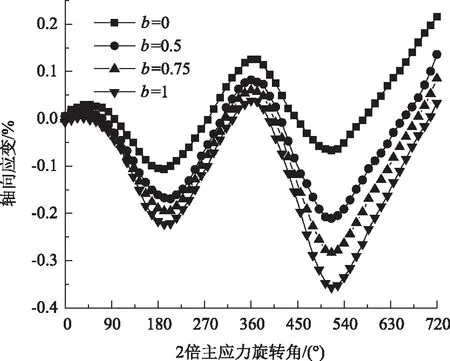
图10 不同中主应力系数下轴向应变曲线Fig.10 Axial strain curves under different intermediate principal stress coefficients
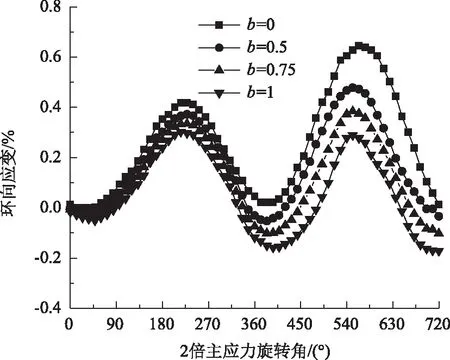
图11 不同中主应力系数下环向应变曲线Fig.11 Hoop strain curves under different intermediate principal stress coefficients
由图11可知,不同中主应力系数下,环向应变随α的变化趋势基本一致。当b=0时,试样主要处于压缩状态;随着b值的增大,压缩变形逐渐过渡到拉伸变形状态,且环向变形逐渐表现出循环压缩- 拉伸的波浪式变化趋势;α旋转到180后°,各个中主应力系数下的环向应变速率明显加快,但是塑性应变增量却随着b的增大而减小。总体上,试样环向变形的变化趋势与试样轴向变形的变化趋势相反。
中主应力系数b的大小体现了第2主应力对试样径向的约束能力,b的改变会引起平行于径向的第2主应力发生很大变化,这就引起径向应变的变化。由图12可知,当b=0时,试样的变形值为负值,表现出明显的拉伸特性,且形变接近于直线变化。当b=1时,试样的变形值全部为正,表现出明显的压缩特性;当b=0.5和b=0.75时,变形处于有拉伸变形转化为压缩变形的过渡区域,b越大,试件径向应变的波动性也逐渐显现,但是应力应变的非共轴特征不能很好地从径向应变曲线上表现出来。总体上,在不同b的作用下,随着α的增大,试件的径向应变基本呈线性变化。
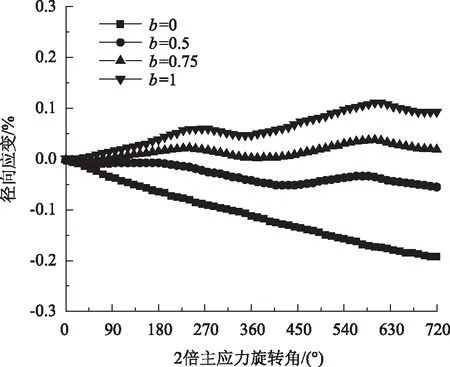
图12 不同中主应力系数下径向应变曲线Fig.12 Radial strain curves under different intermediate principal stress coefficients

图13 不同中主应力系数下剪切应变曲线Fig.13 Shear strain curves under different intermediate principal stress coefficients
由图13可知,在不同b下,试样的剪切应变与不同q下的变形特性基本一致。随着α的增加,剪切应变呈现出压缩-拉伸的变化趋势,且以剪切应变γzθ=0为对称轴呈现出较好的对称性。随着b的增大,峰值剪切应变也在增大,但土样总变形量远小于q改变引起的总变形量。
3 应力应变非共轴特性
3.1 非共轴角的定义
传统经典的塑性理论是基于金属材料各向同性建立起来的,此理论的应变增量与应力共轴,故可采用正交流动法则来建立应力-应变本构方程,同时在特定假设基础上的岩土材料也满足应变增量与应力共轴的特性。对于工程实际中的岩土材料而言,由于岩土材料的组成、胶结方式和所受应力不同,岩土材料呈现出各向异性的特征,且在复杂应力路径下岩土材料的力学特性及变形规律并不能满足正交流动法则的规律,使得塑性应变增量与应力方向出现了不同向的现象,即应变增量与应力的非共轴特性。为了表征主应力轴旋转条件下的非共轴特性,现引入非共轴角的概念,定义非共轴角βtol为主应变增量方向和主应力方向的夹角[16-17],即:
βtol=βdε-α,
(1)
(2)
(3)
式中,α为主应力旋转角;βdε为主应力方向与竖向线的夹角;α,βdε的计算准线方向为竖直方向;dγzθ为扭剪应变增量;dεz为轴向应变增量;dεθ为环向应变增量;σz为轴向应力;σθ为环向应力;τzθ为扭剪应力。
从空心圆柱饱和粉质黏土试样在主应力轴纯旋转应力路径作用下的试验,得出各个应变随着主应力轴方向角的变化趋势。利用主应变增量计算式(2)和主应力方向角计算式(3)计算得出不同q和不同b下的非共轴角βtol。
3.2 不同偏应力q条件下饱和粉质黏土的非共轴特性
当b=0.5时,不同偏应力q条件下βtol随α的变化曲线如图14所示。
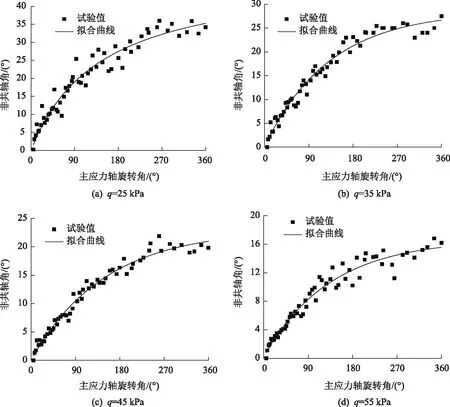
图14 不同偏应力下非共轴角的特征曲线Fig.14 Characteristic curve of non-coaxial angle under different deviatoric stresses
由图14可知,非共轴角βtol随α的增长呈现出随机波动点变化的趋势。在α变化的初期阶段,βtol由0°逐渐增大、增大速率较快;在α位于0°到90°的范围内,βtol相邻点的变化波动较小,增加趋势接近线性变化;当α增大到90°后,各个相邻βtol的散点波动性增强,但增大速率逐渐变小;随着q的增大,相同α对应的βtol逐渐缩小;当q为25 kPa时,βtol的最大值大约为35°;当q为35 kPa时;βtol的最大值大约为27°;当q为45 kPa时,βtol的最大值大约为22°;当q为55 kPa时,βtol的最大值大约为17°。
不同q值下,βtol与α之间满足:
(4)
式中ax和bx为拟合参数。
通过不同q值下βtol与α的拟合曲线,得到ax和bx的值。通过这两个值与相对应的偏应力建立函数关系(见表3),从而可得到q值与βtol的关系。
对表3中的数据进行拟合,得到试验数据和拟合曲线的对比图(图15)。
q与参数ax,bx的拟合方程为:

表3 拟合参数ax,bx与偏应力的关系Tab.3 Relationship of fitting parameters ax,bx with partial stress
ax=-0.89q+68.89,
(5)
bx=1.90q+95.75。
(6)
将式(5)~(6)代入式(4),得到q与βtol之间的函数关系为[18-19]:
(7)
3.3 不同中主应力系数条件下饱和粉质黏土的非共轴特性
当q为35 kPa时,不同b条件下βtol与α的变化曲线如图16所示。
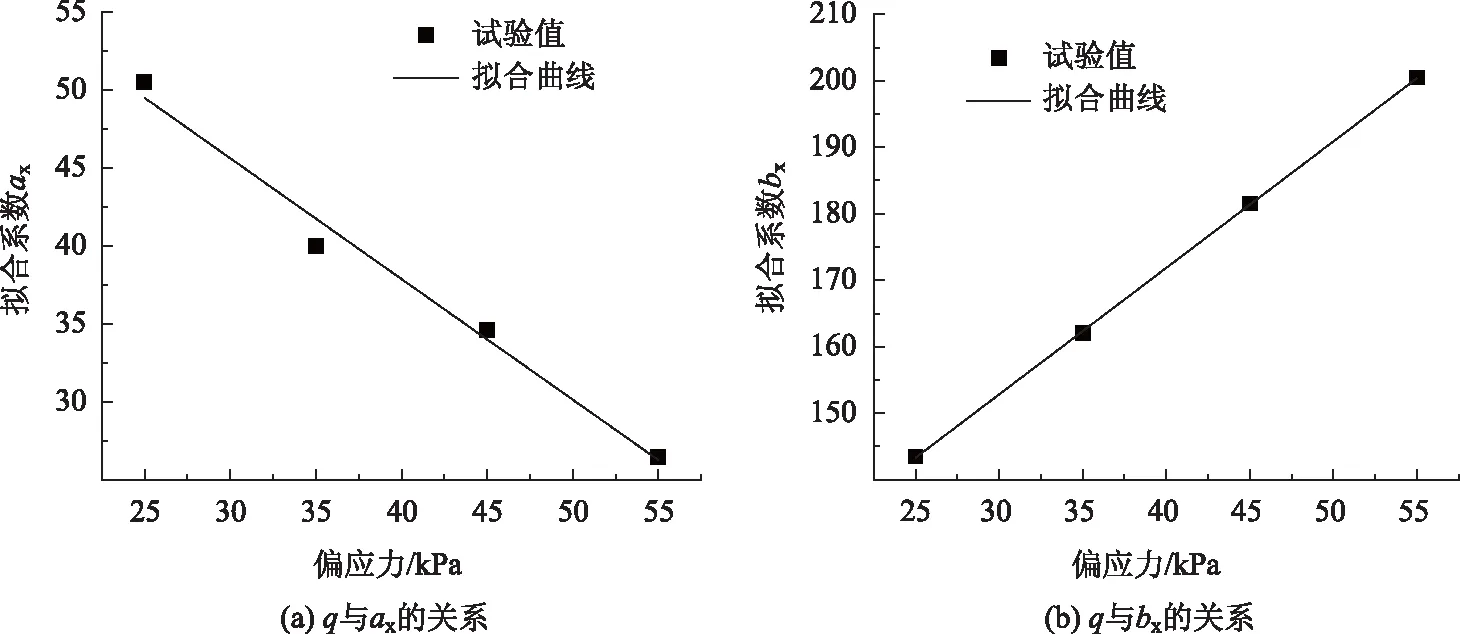
图15 不同偏应力值与拟合参数的关系Fig.15 Relationship of different deviant stress values with fitting parameters

图16 不同中主应力系数下非共轴角的特征曲线Fig.16 Characteristic curve of non-coaxial angle under different intermediate principal stress coefficients
由图16可知,随着α的增加,试样呈现明显的非共轴特性,与相同b值、不同q值的变化规律相似。在加载过程开始阶段,βtol从0°迅速增加,即主应力方向与应变增量方向偏差角度增大;随着α的继续增加,非共轴特性逐渐趋于平稳状态;在α达到90°前,随着α的增加,βtol变化速率较快,当达到α90°之后,βtol变化的波动性变大;b越大,α旋转相同度数时对应的βtol越小。
不同q下,βtol与α之间满足:
(8)
式中cx和dx为拟合参数。
通过不同的b下βtol与α的拟合曲线,得到cx,dx的值。通过两个值与相对应的b建立函数关系(见表4),从而得到b与βtol的关系。
对表4中的数据进行拟合,得到试验数据和拟合曲线的对比图(图17)和拟合方程。
cx=-3.42b+41.61,
(9)
dx=-12.55b+167.45。
(10)
将式(9)~(10)代入式(8),得到b与βtol的关系为:
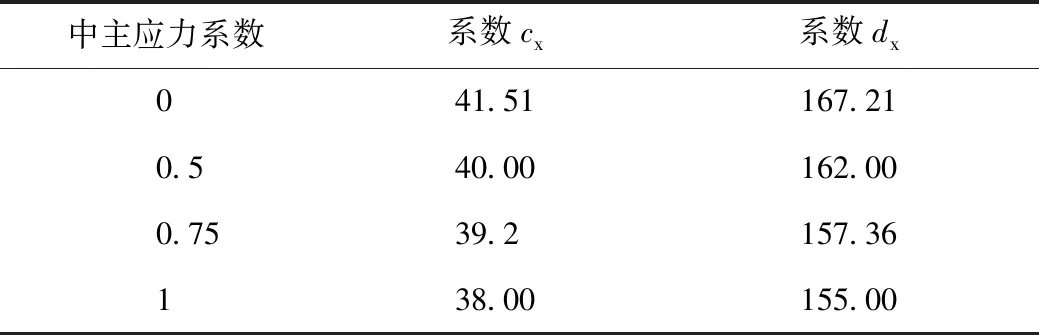
表4 拟合参数cx, dx与偏应力的关系Tab.4 Relationship of fitting parameters cx, dx with partial stress
(11)
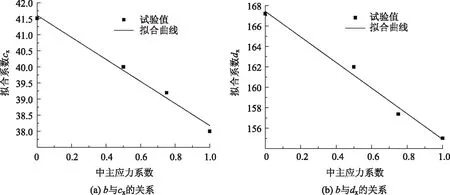
图17 中主应力系数与拟合参数的关系Fig.17 Relationship of intermediate principal stress coefficient with fitting parameters
4 结论
本研究对主应力轴纯旋转应力路径下的饱和粉质黏土进行了不同q值和不同b值的对比试验,研究了这两个参数对空心圆柱饱和粉质黏土试样应力应变、非共轴特性的影响,主要结论如下:
(1)在整个主应力轴旋转角增加过程中,q较小时轴向应变量呈现为正负值周期性变化的特征,土试样呈现为拉伸-压缩循环交替变形的特性。当q增大后,试件的拉伸状态越明显;在α为180°时,所有偏应力下的应变会趋向于一个平衡值的状态,各条曲线基本重合。
(2)不同中主应力系数下,环向应变随α的变化趋势基本一致。当b=1时,饱和粉质黏土试样主要处于压缩状态。随着b的减小,压缩变形逐渐过渡到拉伸变形状态,且环向变形逐渐呈现出循环压缩-拉伸的波浪式变化趋势。
(3)随着α的增加,试样呈现明显的非共轴特性。与相同b值、不同q值的变化规律相似。在加载过程开始阶段,βtol从0°迅速增加,即主应力方向与应变增量方向偏差角度增大。随着α的继续增加,非共轴特性逐渐趋于平稳状态;在主应力旋转角达到90°之前,随着α的增加,βtol变化速率较快;当达到90°之后,βtol变化的波动性变大;b越大,α旋转相同度数时对应的βtol越小。
(4)βtol随α的增长呈现出随机波动点变化的趋势。在α变化的初期阶段,βtol由0°逐渐增大,且增大速率较快;在α位于0°~90°的范围内,βtol相邻点的变化波动较小,增加趋势接近线性变化;当α增大到90°后,各个相邻βtol的散点波动性增强,但增大速率逐渐变小;随着q的增大,相同α对应的βtol逐渐缩小。
