基于特征根的结构强度试验控制系统参数优化
2020-06-18牧彬
牧 彬
(中国飞机强度研究所,陕西 西安 710065)
在全尺寸飞机结构强度试验过程中,协调加载控制系统中控制参数对系统各加载点的跟随性、稳定性、动态性能及稳态误差都有较大影响。其中,系统稳定性对试验人员及试验件至关重要。协调加载控制系统稳定性主要是指各加载点抑制振动的能力,不合适的控制参数会降低各加载点闭环控制系统的稳定性,容易引起自激振动,或被外界干扰信号激起振动,威胁试验件安全及试验人员安全,成为结构强度试验过程中,控制人员面临的主要危险点。
目前,国内在协调加载控制系统参数优化研究方面起步较晚,主要采用系统建模结合新型控制率进行仿真的方式,包括自适应PID、模糊PID及滑膜变结构控制等方式方法,将闭环控制系统动态性能及稳态误差作为研究指标,系统稳定性只作为一般满足项。同时,新型控制率与实际试验过程中使用的协调加载控制器结合较差,导致研究多数停留在仿真阶段,对试验参数配置指导作用较弱。
工程试验过程中多采用性能成熟稳定、安全保护措施可靠的协调加载控制器,主要有MTS及MOOG两类型设备。为保证设备可靠性,控制器开放程度较低,采用基本比例积分微分或比例积分阻尼的控制方法,实时在线整定参数难度较高。参数优化时,为提前化解隐患及风险,需将系统稳定性分析放在首位,通过稳定性分析,给出参数取值范围,在该范围内,再对系统动态性能及稳定精度进行考核,最终实现参数优化的目的。
控制系统闭环特征方程的根称为闭环特征根,闭环控制系统稳定的充分必要条件是特征根全部具有负实部,也就是特征根全部位于s平面的左侧。因此,通过计算指定控制参数下,系统特征根的分布情况,能够对系统稳定性进行判断,进而得到系统稳定前提下参数分布情况。
本文通过建立协调加载控制系统数学模型、简化执行机构及试验件数学模型,计算控制系统闭环特征方程,以阻尼参数为例,计算不同阻尼参数条件下的闭环系统特征根,以特征根分布作为判断系统稳定与否的条件,为阻尼参数优化提供取值范围。该方法适应性好,计算量少,可直接用于指导实际系统参数选择,具有广阔应用前景。
1 控制系统建模
在控制系统建模过程中,忽略数模转换及模数转换等非考核环节,先将系统按模块进行划分,如图1所示,图中Command代表输入信号,Feedback代表结构响应信号,Control代表控制模块,Model代表被控对象模块,Sensor代表传感器模块[1]。
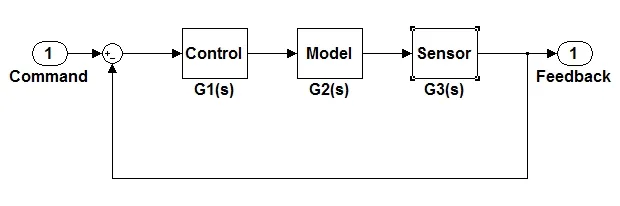
图 1 控制系统模型
从结合工程应用角度出发,考虑对实际控制器的指导作用,采用与MOOG协调加载控制器相同的控制规律[2],如图2所示,其中Kp代表比例参数、Ki代表积分参数、Kd代表阻尼参数。
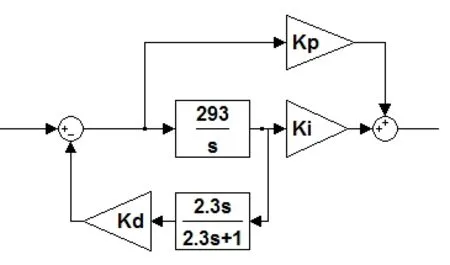
图 2 控制模块建模
被控对象模块建模时,需考虑电液伺服阀、液压作动器、连接件及飞机结构,如图3所示,图中Valve、Actuator、Connection、Structure分别代表上述功能模块。

图 3 被控对象建模
传感器模块建模较为简单,测力传感器量程选取原则是要求设计载荷最大值等于满量程的60%~80%,因此其工作范围在传感器线性区间内,测力传感器传递函数可简化为增益环节。
2 系统传递函数
在建立控制模块传递函数时,需对阻尼参数的负反馈环节进行简化。将其引入点前移,构成前项传递函数为1的负反馈环节,再与比例积分环节相乘,得到控制模块传递函数,如式(1)所示。

对式(1)进行简化,得到式(2)。
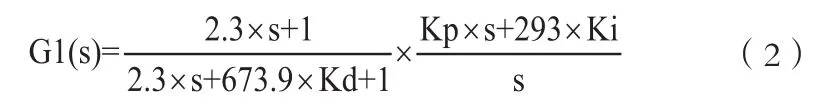
将式(2)中多项式合并展开,得到式(3)。
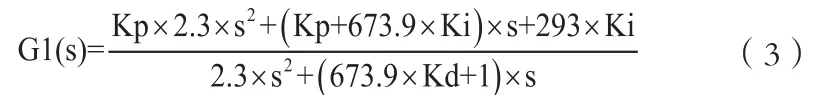
电液伺服加载的作动器与连接件及飞机结构的等效负载可以看作刚性连接,测力传感器也就有较大刚度,可以忽略测力传感器的弹性变形,将整个被控对象当作一体进行研究[3]。
其中,伺服阀流量方程如式(4)所示。

式(4)中:Kq是伺服阀流量系数(m2/s);QL是伺服阀负载流量(m3/s);Xv是伺服阀阀芯位移(m);PT是液压油箱的压力(Pa);Ps是液压源压力(Pa);PL是伺服阀负载压力(Pa);w是伺服阀口控制的面积梯度(m);ρ是液压油的密度(kg/m3);Cd是伺服阀口的流量系数。
液压作动筒压力如式(5)所示。

式中,YL是负载等效位移(m);AF是液压缸的活塞有效面积(m2);Vt是液压缸两腔的总体积容积(m3);Ctc是液压缸的总泄漏系数;Be是液压油的等效体积弹性模量(Pa)。
实际施加载荷如式(6)所示。
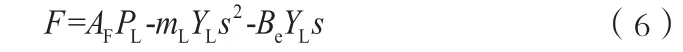
由于伺服阀及液压作动器传递函数不是本文研究重点工作,故对其进行符合工程应用的降阶处理,将被控对象模块与传感器模块合并简化,得到二阶线性系统[4],作为研究内容,如式(7)所示。
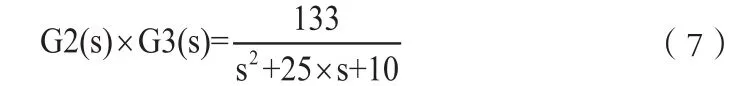
整个系统的开环传递函数可由式(3)及式(7)相乘后得到。
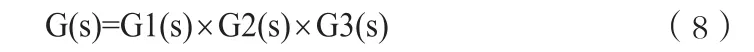
系统此时简化为开环传递函数为G(s)的单位负反馈系统。
3 计算方法
在计算系统闭环特征根之前,由于本文以阻尼参数为例进行研究,故可以将比例及积分参数代数化,整个计算过程中,比例及积分参数保持不变,简化整个计算量。假设比例参数为3、积分参数为1,阻尼参数为自变量。
在MATLAB中输入以下程序,得到符号计算表达式。>> syms s kd
>> fx1=(2.3×s+1)×133×(3×s+293)
>> fx2=(s^3+25×s^2+10×s)×(2.3×s+1+673.9×kd)
>> fx3=fx1+fx2
fx3=
(s^3+25×s^2+10×s)×((6739×kd)/10+(23×s)/10+1)+(3×s+293)×((3059×s)/10+133)
由以上可知,系统为四阶方程,想要计算四个特征根与自变量阻尼参数Kd之间的函数表达式,较为困难。因此,分别给阻尼参数赋值,再计算四个特征根的方法简单易行,同时计算量少,利于快速筛选使得系统稳定的阻尼参数取值范围,为工程试验提供直接指导。
在MATLAB输入以下程序,可得到系统特征根,其中阻尼参数为0.01。
>> k=(s^3+25×s^2+10×s)×((6739×0.01)/10+(23×s)/10+1)+(3×s+293)×((3059×s)/10+133)
>> t=solve(k)
4 结果及分析
分别以阻尼参数为1、0.1、0.01为例,计算三组闭环特征根,结果如表1、表2、表3所示。
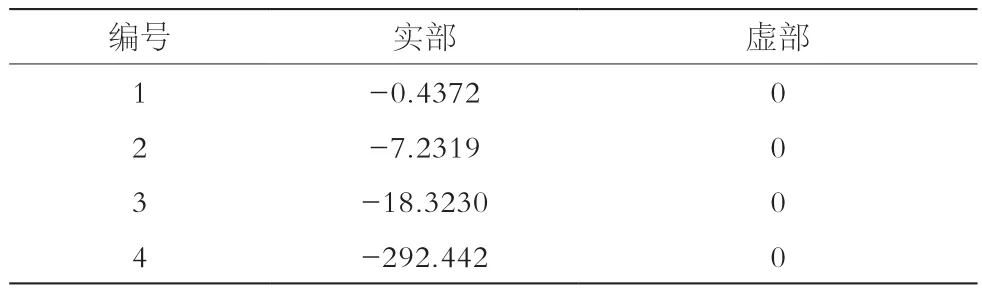
表1 阻尼参数为1时闭环特征根
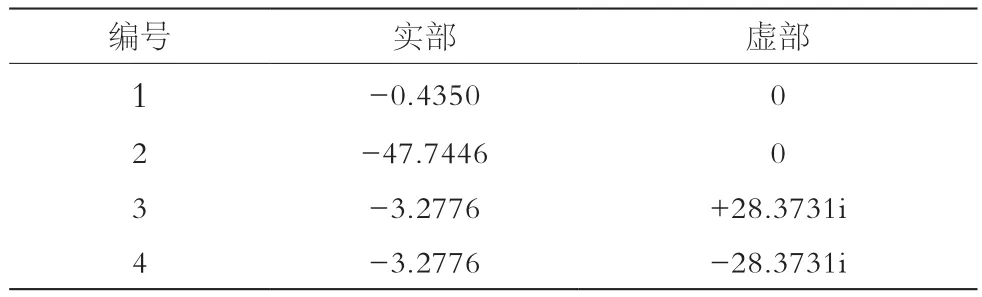
表2 阻尼参数为0.1时闭环特征根
由以上可知,随着阻尼参数变化,系统闭环特征根出现明显变化。其中,复数根的实部明显出现向坐标轴右半平面的移动趋势,也就是系统逐渐变得不稳定,开始出现发散现象。
对于工程试验,过小的阻尼系数容易引起振动,因此系统调试过程中,阻尼参数首先应设置较大,当液压系统执行完加压动作后,施加最大载荷的10%调试跟随性,再根据系统跟随性逐渐减小阻尼参数,始终保证系统要有足够的稳定性,避免振动现象出现,危及试验件安全。
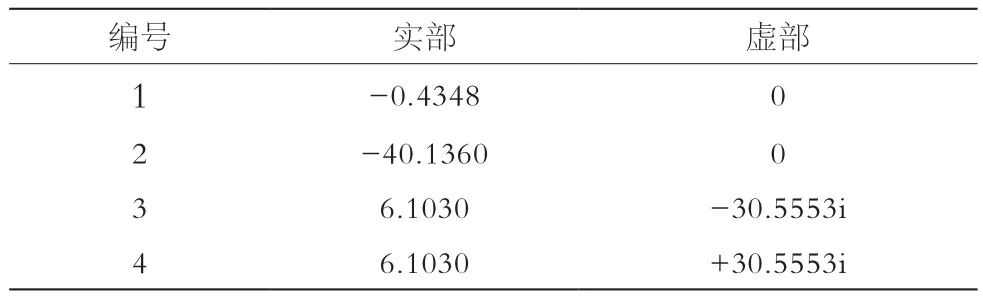
表3 阻尼参数为0.01时闭环特征根
5 总 结
本文通过建立结构强度试验控制系统模型,建立各环节传递函数,计算系统闭环特征方程,利用求解器计算给定参数条件下系统特征根的分布,依据系统稳定的充分必要条件判断系统稳定性,为工程试验参数配置提供直接依据,为提高控制系统稳定性提供直接计算方法。
