浅议导数在竞赛中的解题应用策略

郭铭纪

(福建省泉州第一中学 362000)

一、夯实基础，正确求导

解答该类试题的策略一般应牢记以下内容：其一，保证求导结果的正确性.同时，注意函数的定义域，为后面的解题奠定基础.其二，在涉及参数的函数中，进行分类讨论.

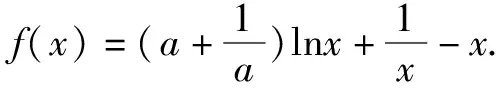
(1)设a>1，讨论f(x)在区间(0，1)上的单调性.

(2)设a>0，求f(x)的极值.

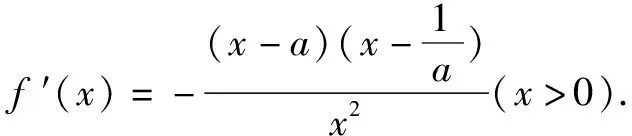
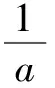
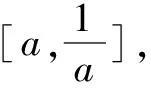
二、灵活应变，巧妙转化

解答部分高中数学竞赛试题时，需要在认真审题基础上，融汇贯通所学，突破惯性思维，才能找到解题思路.一方面，深入分析题干问题，能够透过现象看本质，结合问题形式，大胆设想，通过构造函数，运用导数进行分析.另一方面，解题时应认真推理，确保上下推理的严谨性，尤其有“=”存在时，应明确“=”成立的条件.

例2(2019年全国数学联赛福建赛区预赛)已知f(x)=ex.

(1)略；(2)求证：当x>0时，f(x)>4lnx+8-8ln2.

解析令g(x)=ex-4x，则g′(x)=ex-4.当x∈(-∞，ln4)，g′(x)<0;当x∈(ln4，+∞)，g′(x)>0.则g(x)的最小值为g(ln4)，即g(x)≥g(ln4)=4-4ln4，即g(x)=ex-4x≥4-4ln4，则ex≥4x+4-8ln2，当且仅当x=ln4时取“=”.

∴f(x)-4lnx-8+8ln2≥(4x+4-8ln2)-4lnx-8+8ln2=4x-4lnx-4，当且仅当x=ln4时取“=”.

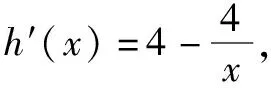
综上f(x)-4lnx-8+8ln2≥4x-4lnx-4≥0，且“=”成立的条件不同，∴当x>0时，f(x)>4lnx+8-8ln2.

三、注重拓展，提升能力

为使学生能够运用导数顺利解答高中竞赛中一些难度较大的题目，一方面，深入讲解导数表示的几何含义，理解导数的本质，保证在解题中正确运用.另一方面，适当为学生讲解一些拓展内容，如为学生讲解导数的导数，并结合相关竞赛试题的讲解，使学生牢固掌握，在竞赛中能够迅速找到解题思路.

例3(2018年河北高中数学竞赛)已知曲线f(x)=ex-1和曲线g(x)=lnx，分析两个曲线的公切线的条数.

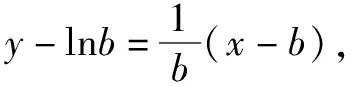
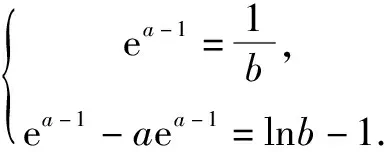
消元得到ea-1-aea-1+a=0，方程根的个数即为两曲线公切线条数.

令m(x)=ex-1-xex-1+x，则m′(x)=1-xex-1，m″(x)=(-1-x)ex-1.

当x<-1时，m″(x)>0，m′(x)为增函数，当x>-1时，m″(x)<0，m′(x)为减函数，且当x<0时，m′(x)>1，m′(1)=0，即，x=1是m′(1)=0的根.

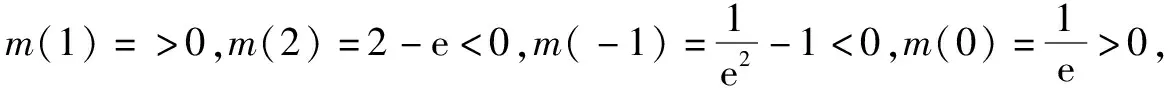
综上可知方程ex-1-xex-1+a=0有两个不同的根，因此，两条曲线的公切线共有两条.