数学抽象下的高中教学设计研究

胡昌亮

(江苏省镇江心湖高级中学 212132)

“核心素养”是近几年众多教育专家学者热议的主题，也是数学课程目标的集中体现.由于数学学科本身与现实世界的联系是抽象的，所以作为六大核心素养首位的数学抽象素养的提出是必然的；其次，当前教育的主要形式是学校教育，课堂又是学校教育的主阵地，所以有效的教学设计尤其是以培育高中生的抽象素养为目的的课堂教学设计是有意义的.

纵观现状，我国专家学者如史宁中教授等对“核心素养”的研究已经非常深刻，但如何针对高中生的数学抽象素养进行教学设计的研究却不多见.

数学研究的对象是现实世界抽象的产物，理性思维的形成需要数学抽象的奠基.作为一种思维过程和能力，数学抽象可让高中生养成思考问题的一般性习惯，把握数学本质，更可以渗透到其他相关学科中去，解决相关问题.抽象思维能力作为数学思维能力的一种，在建构数学知识的过程中起到主要的支撑作用.高中生一般生理年龄在十六岁至十九岁之间，他们已经形成了较为成熟的逻辑思维和认知水平，但并不代表他们就不需要继续培养数学抽象素养，与其他素养不同的是数学抽象需借助数学知识作为载体，通过系统的训练才可以获得.因此在课堂教学设计中引入数学抽象素养，对学生的能力结构的塑造也非常有意义.

史宁中教授将数学抽象划分为数量与数量关系的抽象，图形与图形关系的抽象，虚拟和现实的抽象.要拿下数学抽象问题，感性认识和直观体验的结合是中学教学的第一要务.

数与形是刻画事物本质的两个重要方面，数无形不直观，形无数不入微.“数”抽象难懂，“形”形象直观.数形结合思想是数学中解决问题的重要思想方法，可使复杂问题简单化，抽象问题具体化，最终达到优化解题方法的目标.

教学片断1：已知函数f(x)定义域为R,请你说出对f(x)=f(x+a)的理解，其中a为非零常数.

设计目的：这是函数中众多抽象代数式的一种，蕴含着某些性质的抽象代数式往往会让学生摸不着头脑，无从下手.笔者认为，可借助图形化手段思考代数式，培养数形结合思想，将抽象问题结合具体图形去理解，提高抽象素养.

上述解决过程不仅是数形思想的渗透，还是高中化归思想的一种普及.学生在此次学习之后，在遇到类似抽象代数式时，便可利用函数图象辅助教学，结合现实中一些具体的感知，进而加深对抽象代数式的理解.教师也可以相应给出变式训练，如f(a+x)=f(b-x)揭示了什么数学本质，培养学生的发散思维，加强对所有此类问题的理解，提高学生抽象素养水平.

反之，几何图形虽然直观形象，但要反映数学的本质，还需要借助数的运算；以数论形，可以让学生理解几何图形背后的数学本质.纵观高中数学，空间向量便是此类问题的典型代表，利用空间直角坐标系，将空间中线面位置关系与代数运算建立联系，进而将几何问题代数化.

教学片断2：在四棱锥P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°.

(1)证明：平面PAB⊥平面PAD；

(2)若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值.

设计意图：形数不分家，图形的直观性优点有时候也难以揭示背后的规律，这时候就需要将图形数量化，利用向量，函数，方程等代数手段“以数解形”.

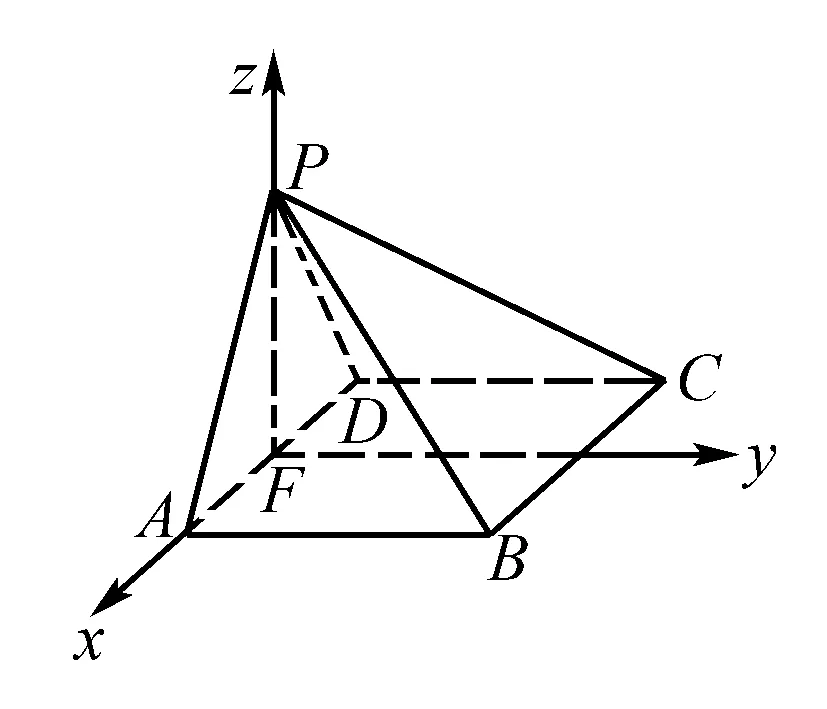
分析与解答第2问中的二面角求解，如果借助于几何手段去寻找并且求解出来，会有一定的难度，对学生的空间思维能力要求过高，于是利用面面垂直性质定理借助于第一问，可建立空间直角坐标系，如图所示，用定量的方法解决几何问题.

简解建立如图所示的空间直角坐标系F-xyz.

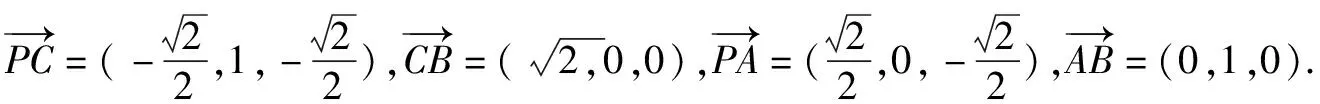
设n=(x,y,z)是平面PCB的法向量，则

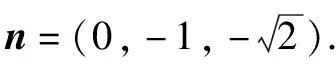
设m=(x,y,z)是平面PAB的法向量，则同理可得m=(1,0,1).后面转化为求两个法向量的余弦，这里省略.

数学中这样的例子还有很多，借助于直观和感官的思维，可以感受数量与数量关系，图形与图形关系的抽象.在高中课堂教学中，我们要善于在教学设计中合理并且善于利用数学抽象，提高课堂教学这个主阵地的效率和价值.