基于双曲空间嵌入的极小值社区划分算法

谢 菁,羿舒文,张 毅

(武汉大学 电子信息学院,武汉 430072)

0 概述

以移动互联网为代表的信息通信网络已经成为现代社会社交的重要媒介,逐渐渗透到人们日常生活的各个方面。互联网的应用日益广泛,也使其产生的数据量呈爆炸性增长趋势[1]。2019年2月,思科全球移动可视化网络指数(VNI)预测全球移动用户将达到57亿,移动数据流量的年数据量将达到930 EB[2]。在此背景下,有效分析移动互联网中用户产生的数据具有重要的社会意义。随着复杂网络规模不断增长,如何定量、有效地分析大规模网络备受关注。现实生活中的复杂网络具有自组织、自相似和小世界特性[3],其中小世界特性表明网络具有节点间平均距离小、聚合系数大、节点度分布服从幂律分布等特点。这些特性是复杂网络为实现某些功能而逐渐演变成拥有特定功能集团的结果。

复杂网络具有社区化特性,每个节点在不同的社区拥有不同的“角色”,其结构的多样性表明复杂网络内部的组织方式也具有多样性。针对复杂网络中特定社区的研究,对于理解网络结构、网络中对象的特征和对象与对象之间的相互关系具有重要价值。社区划分是找到数据相似性并定义分组的过程,其本质是一种使用聚类思想的方法。复杂网络作为众多领域信息网的模型,具体为表示信息资源的节点和表示信息之间关系的连边。因此,在复杂网络上进行社区划分能发现信息聚集、传播和流动关系,比单纯地利用节点本身属性聚类发现社区更有意义。挖掘复杂网络中潜在的社区结构,对于进一步研究网络的拓扑结构、辨识和预测社区功能起到至关重要的作用[4-5]。目前存在多种社区划分方法,它们有各自应用场景和不同侧重,但随着数据量的持续增长,数据处理均面临计算能力的限制。因此,需要设计更能适应大数据环境、保留数据精度的改进算法。

本文针对大型真实复杂网络分析难以保留网络特性和处理大数据量时社区划分复杂度高的问题,提出基于双曲空间嵌入的极小值社区划分算法MHE。将网络嵌入二维双曲空间模型——庞加莱圆盘,以保留复杂网络结构信息。在此基础上,根据节点分布与圆盘中角度的关系得到θ曲线,以双曲角坐标差值表示两个节点间的相似性。通过划分θ曲线保证局部节点相似性最大,即选择曲线极小值处划分社区,并根据最大模块度选择最优社区划分结果。在此过程中无需设定聚类中心,从而避免人为设置聚类中心导致的误差。

1 相关研究

复杂网络分析最初是基于数学的方法展开的。大量交互节点的集合可以建模为图结构,为复杂网络分析提供了理论依据。基于数学的复杂网络分析方法包括矩阵法、图论法和统计法等。矩阵法如非负矩阵分解为深入分析网络中节点和簇之间的关系提供了理论基础。随着网络规模的增加,相比传统图论对网络进行结构化分析,随机图理论能更好地描述大型网络的性质[6]。统计法则侧重于利用随机图模型和小世界网络,可以挖掘具有显著统计特性的复杂网络节点子集,得到准确的计算结果。虽然基于数学的复杂网络分析方法拥有良好的理论基础,但因为其固有的高计算成本,所以不适合大规模网络。随机游走的网络分析方法从网络中的任意节点开始游走,如DeepWalk[7]用SkipGram的方法学习节点特征,当网络中具有清晰的社团结构时,节点在社团内部游走的概率将远高于在社团间游走。随机游走的方法主要针对复杂网络中的结构特性,且步长选择的不同对算法性能影响较大,步长大意味着更多的迭代,而步长取得过小又很难得到最优解决方案。文献[8]通过建立复杂网络的双曲几何框架,表明复杂网络在结构上与双曲空间有高度一致性。在大数据量的背景下,将真实复杂网络嵌入到双曲空间,可以将必须映射到高维欧式空间才能保留的较多性质,在不降低精度的情况下映射到低维的双曲空间,这种发现将真实复杂网络分析问题转化为双曲几何问题,为复杂网络分析提供了新的思路。

社区划分在复杂网络分析中具有重要的社会意义和应用价值。现有的社区划分算法主要有基于图论的算法、基于层次聚类的算法和基于函数优化的算法。基于图论的经典算法有K-L算法[9]和基于图拉普拉斯矩阵特征向量的谱平分算法[10],但由于K-L算法和谱平分算法均为二分算法,因此不适用于包含较多团簇的复杂网络。为检测多社区结构网络,研究者提出基于图半监督学习的标签传播算法LPA[11]和基于LPA的SLPA算法[12]。基于图论的方法涉及矩阵计算,其计算对硬件要求很高,因此,难以适用于大型网络。基于层次聚类的经典算法有GN算法[13],但因为GN算法不适用于大型复杂网络,研究者进而提出基于贪婪的FGN[14]算法,同时定义了重要社区划分评价指标的模块度。基于函数优化的社区划分算法,例如极值优化算法[15],通过求解模块度最优解进行社区划分,也有基于最优模块度提出通过多次迭代最大化模块度进行社区划分的Louvain社区发现算法[16]。文献[17]在谱聚类的基础上进行修正,提出了正则化谱聚类算法。

2 复杂网络与双曲空间

2.1 复杂网络和社区

现实生活中许多领域的网络,如信息网络、生物网络、社会网络等,均可建模为复杂网络的形式。复杂网络具有自组织、自相似和小世界效应[18]。小世界效应指网络拥有无标度性,节点拥有高聚合系数,网络直径不大于O(logan))[6],其中,无标度特性指网络中节点的度分布服从幂律分布,节点的聚合系数是指节点相邻的所有节点之间连边数与这些相邻节点之间最大可能连边数的比值,物理含义为相同节点的两个相邻节点仍然是相邻节点的概率。聚合系数描述了网络的局部聚集特性,可证明复杂网络有明显的社区化特征。

社区一词由德国社会学家TÖNNIES于1887年在《共同体与社会》中提出。TÖNNIES认为,社区是由具有共同习俗和价值观的同质人口所形成的社会集合状态[19]。社区可以看作网络中具有相同偏好节点的集合,是社会关系和社会活动的特定具体方式。由于复杂网络拥有明显的集团化特征,因此区分复杂网络中的社区具有重要的应用价值。

2.2 双曲空间

双曲空间是指曲率为恒定复常数K=-ζ2,ζ>0的非欧空间。二维双曲空间节点坐标用极坐标的方法表示为径坐标和角坐标的形式:(ρ,θ)。假设双曲空间上存在两个点(ρt,θt)和(ρs,θs),两点间的双曲距离为两点间的测地线长度,计算公式为[8]:

sinh(ζρs)sinh(ζρt)cosθst)

(1)

其中,θst表示两个点间角坐标的差值。

负曲率导致双曲空间很难在平面上可视化,但双曲空间上的定理可以通过几何关联性质转换到欧式空间上证明,由此出现了双曲空间的等价分析模型,例如二维双曲空间模型——庞加莱圆盘[20]。该模型将二维双曲空间在平面上可视化为半径为R的平面圆盘,圆盘边界处表示无穷远,双曲直线为两端均垂直于圆盘边界的弧线。

双曲几何与欧式几何的主要不同点为双曲几何不遵循欧几里得第五公设。在双曲空间中,过直线外一点存在至少两条不重合的直线与已知直线平行,如图1(a)所示,并且双曲空间中三角形ABC内角之和小于180°,如图1(b)所示。

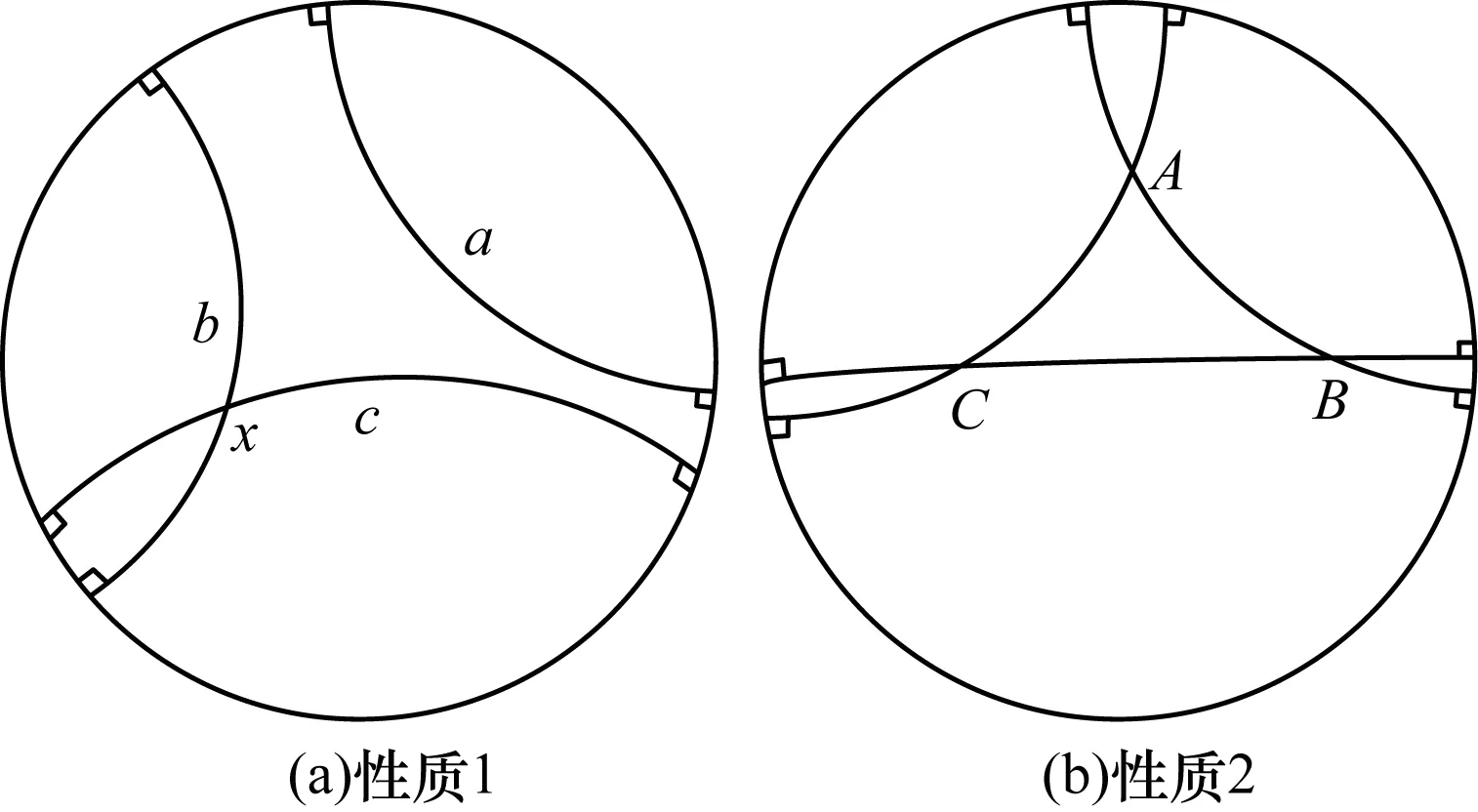
图1 二维双曲圆盘几何性质

2.3 问题描述

信息时代网络数据量迅速增长,如何完整保留复杂网络的信息非常重要。复杂网络节点间的相似性不是单纯依靠节点间的直接连接评判,而更与其树形结构相关,同一子树上的节点相互之间具有一定程度上的相似性,具有相同父节点的子节点具有高度相似性。因此,文献[5]提出了复杂网络的双曲几何框架,用几何的方法研究复杂网络的结构和功能,证实了双曲几何不会破环网络结构的性质并论证了复杂网络嵌入双曲空间的合理性。复杂网络的幂律分布是双曲几何作为潜在几何结构的自然反映,在二维双曲空间中,圆的周长C(r)和面积A(r)计算公式[8]分别如下:

(2)

(3)

可以看出,圆的周长和面积对于双曲圆中的半径r均呈指数增长关系,该特性表明双曲空间能够完整地表现复杂网络的幂律分布特性。双曲随机图模型[21]定义了大小为n所有图的概率分布,当双曲平面中节点距离较小时节点相连,得到的模型具有幂律分布和高聚集性,为真实网络嵌入双曲空间提供了理论依据。

复杂网络与双曲空间的相关研究包括网络生成方法和网络嵌入方法。文献[22]构建了基于二维双曲空间的经典网络生成模型PSO模型,提出了节点流行度和相似度的概念,其中节点径坐标与节点的流行度成反比,节点间的角坐标差值与节点属性相似度成反比。文献[23]提出基于拉普拉斯矩阵的双曲嵌入方法,该算法以庞加莱圆盘模型为保角模型,利用节点度拉普拉斯矩阵的最小两个非零特征值得到双曲角坐标,由于该方法涉及矩阵运算,因此在大型数据下难以适用。文献[24]在双曲随机图模型的基础上提出快速嵌入算法,该算法适用于计算大规模网络基于极大似然估计的双曲嵌入,不依赖昂贵的数值计算及嵌入迅速的优点,使其在真实的大规模网络嵌入中具有较高的应用价值。

本文在快速嵌入算法的基础上提出基于双曲空间嵌入的极小值聚类算法用于社区划分。庞加莱圆盘定义为一组范数小于圆盘半径的复数集合[25],本文将复杂网络嵌入到二维庞加莱圆盘上,保留了网络树形结构,又因为双曲角坐标差值表示节点间的相似度,所以对节点对应角坐标的分布曲线进行极小值划分,得到相邻极小值之间的节点角坐标差值,其物理含义为一个社区,并通过最大模块度值选择最优社区划分。

3 基于双曲嵌入的极小值社区划分

本文将已知连接关系无权无向的真实复杂网络嵌入到二维双曲空间模型——庞加莱圆盘[20]中。二维庞加莱圆盘拥有3个基本参数:径坐标r,角坐标θ和温度T。温度参数用来调整圆盘潜在几何分布,当T→0时,双曲空间越稳定,相应的T越高,双曲空间的随机性越高,一般根据经验将T设置为0.1。根据庞加莱圆盘的双曲几何性质扫描嵌入复杂网络的圆盘,得到节点对应角坐标的分布曲线,并对曲线按极小值划分,得到社区划分结果。

3.1 复杂网络建模

已知网络的节点属性信息,根据节点间的相似度构建节点间的连边,因为本文方法针对的是真实复杂网络,所以要求建模后节点度分布符合幂律分布。将复杂网络的节点和连边作为算法的输入,建模无权无向图得到节点的邻接矩阵,并且根据节点间的连接信息计算节点度。

3.2 双曲嵌入

复杂网络一般表示为邻接矩阵。由于矩阵计算的复杂性,因此本文考虑对复杂网络进行二维双曲空间嵌入,在此过程中会保留网络局部的结构信息,即每个节点的度连接信息,并计算复杂网络每个节点对应在双曲空间二维庞加莱圆盘模型上的双曲坐标,如图2所示。

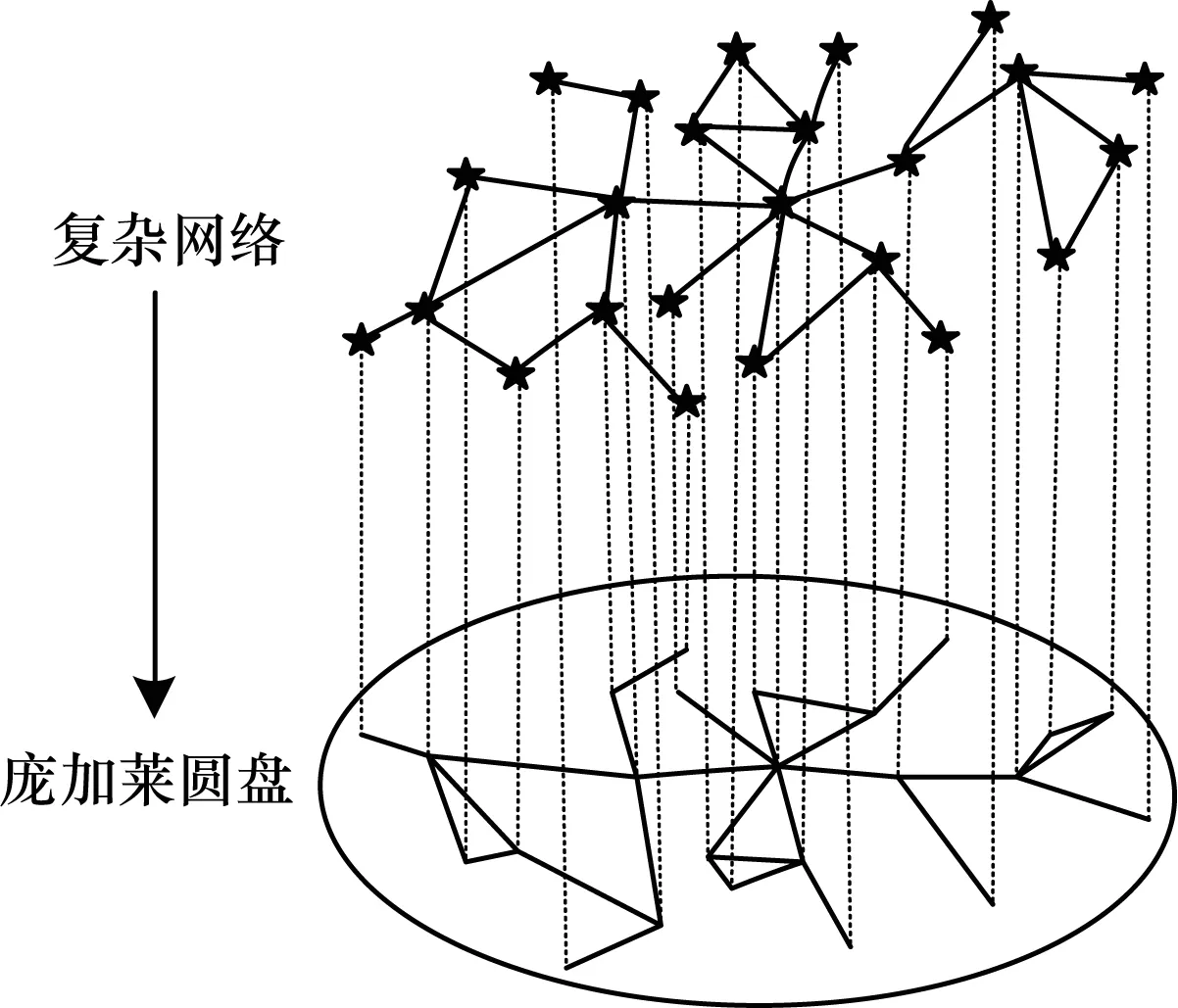
图2 复杂网络嵌入庞加莱圆盘示意图

本文使用快速嵌入算法[24]进行双曲嵌入。在快速嵌入算法中,节点拥有嵌入顺序。根据已知的网络节点与连边信息,确定唯一的庞加莱圆盘。按照节点在网络中的度降序排列得到节点顺序,按照节点顺序从第一个节点开始依次计算双曲坐标。计算庞加莱圆盘半径和双曲嵌入坐标公式的过程如下,详细推导和证明过程请参考文献[24]。

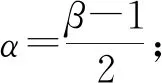
(4)

将节点按度降序排列的顺序依次嵌入,节点i的径坐标计算公式如下:

(5)

其中,deg(i)表示节点i在复杂网络中的度,R表示庞加莱圆盘半径。

同理,按上述节点顺序得到节点i的角坐标,计算公式如下:

(6)

其中,k表示复杂网络中节点i的所有邻居中有k个节点已经嵌入,rj为节点i已经嵌入到双曲空间中的邻居的径坐标,θj为节点i已经嵌入到双曲空间的邻居的角坐标,第一个节点的角坐标在[0,2π]区间中随机生成。

3.3 极小值划分

利用快速嵌入算法[24]将真实复杂网络嵌入到双曲空间二维庞加莱圆盘后,每个节点拥有径坐标和角坐标。由于双曲嵌入考虑了网络性质,因此节点在圆盘上不是均匀分布的。根据PSO模型可知节点径坐标与节点度成反比,节点间角坐标差值与节点的相似程度成反比,而双曲距离可以综合考量节点度和相似度。所以,首先考虑圆盘上角坐标和径坐标分别对双曲距离的影响,固定角度差为45°,固定半径长度为3,分别作径坐标和角坐标对距离的影响曲线,如图3和图4所示。

图3 径坐标对双曲距离的影响

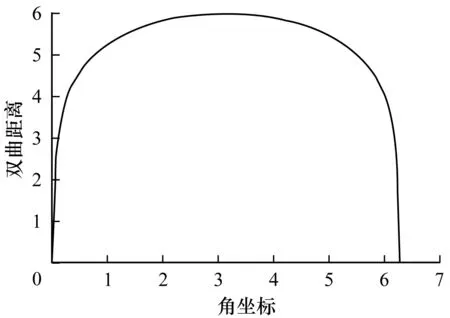
图4 角坐标对双曲距离的影响

可以看出:在径坐标不变的情况下,除了角度趋近于零的情况,角度差对双曲距离变化的影响很小;在角度差不变的情况下,径坐标与双曲距离成正比。复杂网络的集团特性导致节点嵌入后在圆盘上分布不均匀,所以,在双曲圆盘上按照角度划分区域,使角度区域内节点密度大,而在角度区域间节点密度小。因此,本文考虑在节点的双曲角度分布曲线上使用曲线极小值划分实现聚类。

综上,按角度扫描已嵌入的庞加莱圆盘,得到嵌入的节点对应角坐标的分布曲线,称为θ曲线,记为γ(θ)。在θ曲线上寻找局部极小值划分角度区域,使两个局部最小值之间包含一个最大值。

3.4 最优划分条件

本文使用模块度作为选择极小值最优社区划分的条件。模块度是2004年NEWMAN提出的一种衡量社区结构的概念[14],用来描述网络中社区结构内部连边的比例和随机网络中社区内部连边所占比例差值,反映了社区内真实连边数与期望连边数的差异,其值越大,表明节点聚集趋势越大。模块度是社区中的边缘数量减去随机生成图中的期望边缘数量[20],计算公式如下:

(7)

因为θ曲线上的极大值表示圆盘上节点分布稠密处,极小值表示节点分布稀疏处,所以θ曲线相邻极大极小值的纵坐标之差越小,表示节点分布变化越小。因此,定义极值删除规则如下:

定义1(极值删除规则) 寻找曲线上相邻两个极大极小值,使它们的纵坐标值之差最小,将该极大值和极小值删去。

假设当前已经存在θ曲线上k个极小值,根据极值删除规则依次删去极大值极小值,得到极小值点序列集合K={mk,mk-1,…,m2},其中,mk表示该极小值序列包含k个极小值。每个极小值序列对应一种社区划分。对集合K中每个极小值序列计算每个社区划分的模块度,得到模块度集合:

QK={Qk,Qk-1,…,Q2}

(8)

当社区模块度最大时,极小值序列中的极小值为社区划分界限,相邻极小值间的节点属于一个社区,从而得到最优划分社区。最优社区划分目标为:

L=max(QK)

(9)

3.5 基于双曲嵌入的极小值社区划分

综上所述,利用快速嵌入算法,基于双曲嵌入的极小值社区划分算法伪代码如下:

输入节点id,节点id对应节点属性,节点个数n

输出社区划分结果

//步骤1:根据节点属性建模复杂网络

for i in range(n):

for j in range(i+1,n):

if节点i和节点j相似

连接节点i和节点j

根据节点的连接信息得到网络中每个节点的度

for i in range(n):

for j in range(i+1,n):

if节点i和节点j相似

连接节点i和节点j

根据节点的连接信息得到网络中每个节点的度

//步骤2:双曲嵌入

降序排列节点度,生成新的节点顺序

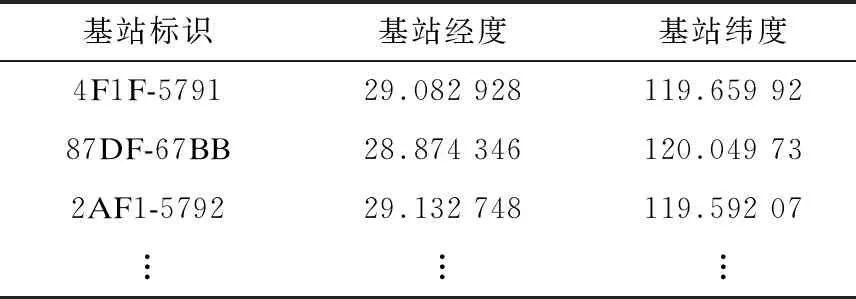
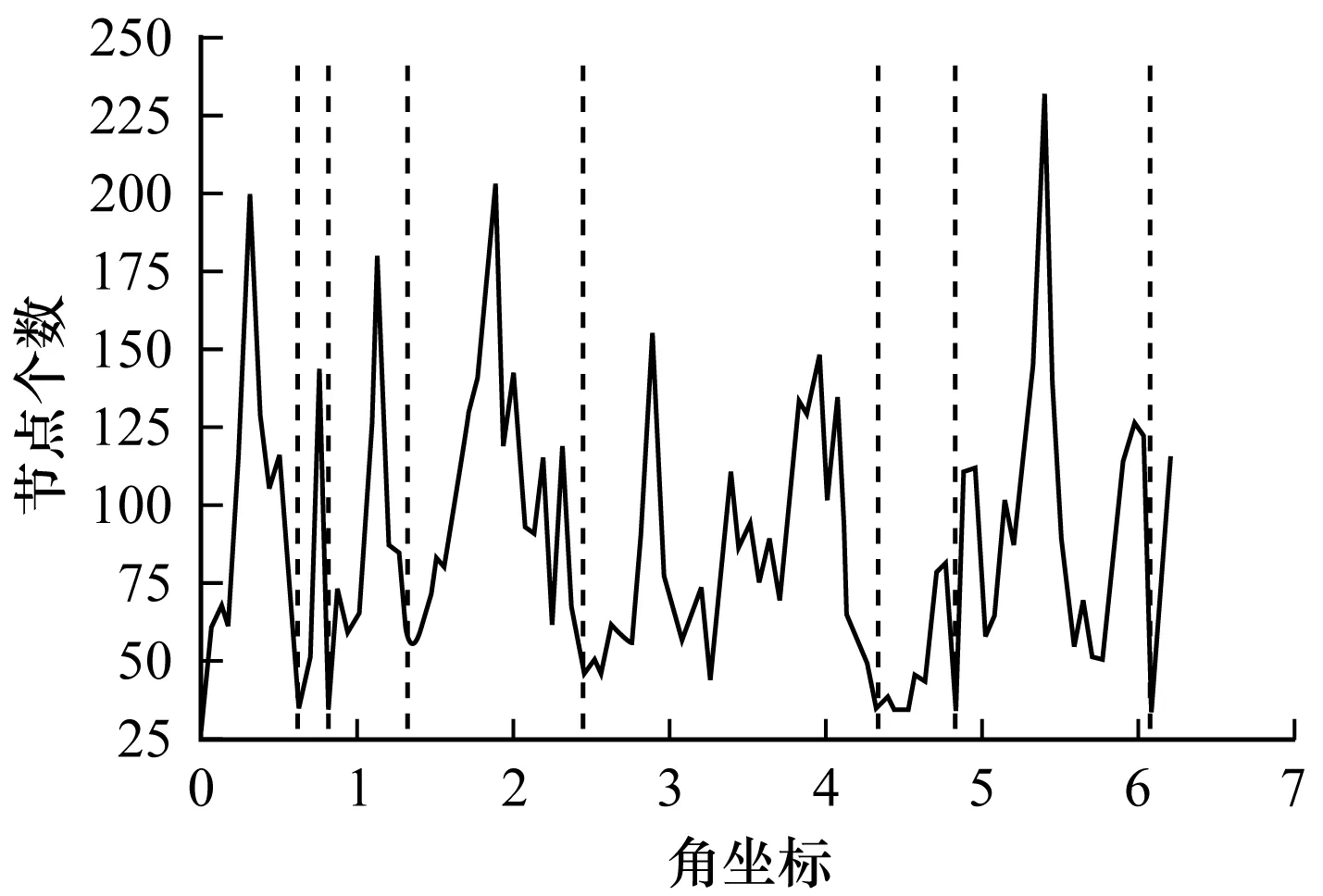
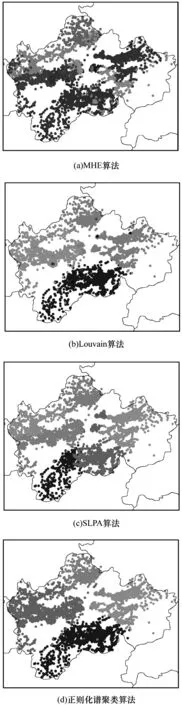
while i

按节点新顺序根据双曲坐标计算公式计算每个节点的ri和θi

计算所有节点的双曲坐标并可视化到二维圆盘上

//步骤3:社区发现

按角度扫描双曲圆盘,得到θ曲线γ(θ),对γ(θ)求导记为γ′(θ)

if γ′(θi-1)<0 and γ′(θi+1)>0

保存θi为极小值

根据极值删除规则,计算模块度集合QK={Qk,Qk-1,…,Q2}

优化目标L=max(QK)得到相应极小值序列

return划分社区和社区个数

步骤1中所述相似性度量可以根据实际情况选择。

4 实验与结果分析

4.1 数据集描述

本文对浙江省某市中国移动的基站真实记录进行复杂网络建模,该市包括8个主要行政区,数据集时间范围是2014年11月21日——2014年12月13日,共计23 d,记录条数超过450万。

每条用户访问记录数据信息包括用户ID、访问基站LAC ID、访问基站CEL ID、访问URL、访问开始时间、访问终止时间等。因为访问记录数据量巨大且本文建模基站合作网络有大量数据信息是不需要的,所以首先对原始数据进行“清洗”。本文建模基站合作网络,假设基站为复杂网络节点,因此,算法中节点间相似性度量方法为两个基站只要服务于共同用户则节点间拥有连边。数据预处理时仅保留数据中基站的LAC ID、基站的CEL ID、基站服务的用户ID,去除基站下的错误用户ID,最后得到每个基站下的用户数据格式如表1所示。

表1 基站用户数据

每个基站节点以LAC ID和CEL ID共同表示,利用LAC ID和CEL ID能够得到基站在地理空间上的真实经纬度,所以,将基站的LAC ID与CEL ID组合作为基站ID,与基站经纬度相对应,去除经纬度缺失基站,得到的数据格式如表2所示。

表2 基站经纬度数据

本文建模基站合作网络,基站间拥有共同用户时表现为两个基站相似,节点间拥有连边,其物理意义为两个基站服务于共同用户,同时可以刻画用户的活动轨迹,所以,对合作网络进行社区划分可以表现基站在真实地理空间上的分布。

4.2 幂律拟合

建模后的基站合作网络为无标度网络。许多学者通过对人类大量行为的动力学研究,发现人类日常行为常有潜在的幂律分布特性[26-27],会表现出幂律分布间隔特性[28-29]。本文建模的基站合作网,其物理含义表现为人的活动方式,由于数据采样时间不包括法定节假日,因此假设在数据采样时间范围内人类行为不会出现较大的地理跨越异常,可使用清洗后的用户访问基站记录数据进行合作复杂网络建模。因此,网络节点度分布应符合幂律分布。

幂律分布表现了真实复杂网络的一种自然形成的节点“排序”性质,由于本文主要研究的网络类型为真实复杂网络,因此首先需要保证实验过程中的数据节点度服从幂律分布。本文使用Python环境下的Powerlaw幂律拟合包[30]拟合建模后的复杂网络节点度分布,拟合结果如图5所示。可以看出,基站合作网络建模得到的网络节点度符合幂律分布特性。

图5 复杂网络节点度幂律拟合结果

4.3 社区划分结果

将建模后的真实复杂网络嵌入庞加莱圆盘,如图6所示,可以看出,圆盘上出现明显的密度分布不均的现象。

图6 建模后复杂网络嵌入庞加莱圆盘的结果

复杂网络嵌入圆盘后,以角坐标为参考得到节点在圆盘上按角度分布的θ曲线。根据θ曲线求导,保证每两个局部极小值中间存在一个局部极大值,并根据极值删除规则选择最优模块度下的极小值。θ曲线的最优划分结果如图7所示,其中,横坐标表示双曲角度,纵坐标表示当前角度节点个数。

图7 极小值划分结果

4.4 实验结果对比

针对真实复杂网络,将本文算法MHE与3种类型的社区发现算法进行对比,分别为在LPA上改进的SLPA算法[12]、基于函数优化的Louvain算法[16]和基于谱聚类的正则化谱聚类社区发现算法[17]。

使用模块度评估社区划分的优劣,计算MHE、Louvain、SLPA和正则化谱聚类算法对合作网络社区划分后的模块度,如图8所示。

图8 4种算法的模块度

由于本文合作网络的物理含义体现了基站的相对地理位置,因此利用基站的真实经纬度将MHE、Louvain、SLPA和正则化谱聚类算法将真实数据集的社区划分结果投影在地图上,如图9所示。其中,Louvain为最优化模块度的方法,正则化谱聚类和Louvain的值类似,与本文算法模块度的值都仅相差仅为0.04。模块度评价仅考虑到网络拓扑结构,可以看出:在实际应用场景下,本文算法对社区进行了更细致的划分,在地理位置上呈现出明显的区域性,在区域划分与地理位置上与该市的行政划分基本吻合;Louvain和正则化谱聚类只是划分出了大的区域,缺少细节划分;MHE相较于Louvain和正则化谱聚类有更高的实际应用价值;SLPA结果的模块度相对较低,在合作网络中有一部分节点未找到其归属社区。

图9 4种算法的社区划分可视化结果

Louvain首先将网络中每个节点作为一个独立的社区,依次将每个节点分配到每个邻居节点所在的社区,计算分配前后的模块度,取模块度最优,该迭代过程与网络节点个数相关;SLPA是先对网络中每个节点给定一个标签,遍历每个节点的邻居确定当前邻居,其计算过程和效果与迭代次数和网络节点个数相关,而迭代次数又明显地影响了计算复杂度;正则化谱聚类基于矩阵运算,而矩阵运算与网络规模关系紧密,本身对计算复杂度和空间复杂度要求都很高;虽然MHE的优化目标也是最优模块度,但其优化过程仅与θ曲线极小值点个数相关,其复杂度主要体现在双曲嵌入,而嵌入过程无需迭代,仅与节点个数线性相关。

5 结束语

在复杂网络数据迅速增长的背景下,现有社区划分算法难以在保留数据精度的基础上准确选择社区中心。针对该问题,本文提出一种基于双曲空间嵌入的极小值社区划分算法。将大型复杂网络建模为图的形式嵌入到二维双曲空间模型——庞加莱圆盘中,利用圆盘上几何对应的物理意义对其中节点对应角坐标的分布曲线进行极小值划分,每两个相邻极小值之间为一个社区。本文算法应用复杂网络的双曲模型理论,保留复杂网络结构特性,无需设定聚类中心,可根据优化目标选择最优社区划分结果。基于中国移动用户访问记录的真实数据对算法进行有效性评估,结果表明,该算法在真实复杂网络中能够取得较好的社区划分效果。下一步将探究复杂网络与双曲几何的映射关系,利用几何方法简化复杂网络分析过程。