移动边缘计算中卸载策略与功率的联合优化
2020-06-18石雪琴刘一勋
余 翔,石雪琴,刘一勋
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 概述
随着互联网的发展,多种多样的新型数据业务极大地丰富了用户日常移动应用的体验[1],如人脸识别、交互式游戏和虚拟现实技术等[2]。但由于移动设备(Mobile Devices,MD)的资源有限,无法频繁处理占用资源较高的业务[3-4]。而移动边缘计算(Mobile-Edge Computing,MEC)的出现弥补了这些能力受限设备的不足,通过将密集型计算任务卸载到边缘服务器可以为设备扩展容量和降低能耗[5-6]。计算卸载是MEC的关键技术之一,也是MEC系统实现终端业务实时化处理的重要手段[7],实验结果表明,将任务卸载到MEC上,可以减少高达88%的时延和93%的能耗[8]。
文献[9]研究了移动设备中具有能量收集功能的MEC系统,并提出了基于Lyapunov优化的动态计算卸载算法。文献[10]使用马尔可夫决策过程执行随机计算任务调度,并通过一维搜索算法得到了最佳的卸载决策。文献[11]提出分段凸优化方法,该方法通过次梯度优化方法有效地解决执行延迟最小问题。文献[12]研究了云和边缘云之间的协作,将联合通信和计算资源分配问题转化为等效的凸优化问题,并制定了资源分配策略。上述文献专注于最小化时延的研究,然而能耗对于用户的体验质量也是至关重要的。文献[13]设计了一种前、后向链路联合优化的计算卸载策略,通过改进的人工鱼群算法对时延和能耗进行优化。文献[14]将计算任务表示为约束马尔可夫决策过程,该过程基于应用特性和无线电环境统计行为的先验知识预先计算的离线策略。文献[15]考虑了一种基于时分多址的多用户边缘计算卸载系统,使用次优分配算法来优化通信和计算资源。文献[16]提出节点与云之间协同卸载,应用拉格朗日乘数法在KKT约束条件下获得最优值。
在计算卸载过程中,传输数据产生的高能耗和高时延大幅降低了用户的体验质量。而传输功率则是影响卸载传输时延和能耗的主要因素,因此本文采用二分搜索法求得用户最佳传输功率以提高用户的体验质量。将多用户计算卸载决策问题制定为非合作博弈,证明集中式优化多用户计算卸载解决方案是NP-hard,并且将最小化计算开销问题制定为混合整数非线性规划(MINLP)问题,提出基于博弈论的功率优化卸载算法,从而降低系统成本和提高用户体验质量。
1 系统模型

图1 移动边缘计算环境模型
1.1 通信模型
本文将A={a1,a2,…,aN}表示所有MD的决策集合,其中,an=0为本地计算,an>0为计算卸载。与本地计算相比,计算卸载降低了时延和能耗,但在传输数据时花费了额外的时间和能耗,即通信时延和能耗。根据Shannon-Hartley,将通信模型定义为:
(1)
其中,ω表示信道带宽,pn表示用户n的传输功率,hn,m表示移动用户n和基站之间的信道增益,σ2表示高斯白噪声功率,pihi,m表示其他用户i与用户n选择同一信道进行计算卸载产生的干扰。
1.2 计算模型
本文用Θn≜(dn,cn)表示MD的计算任务,dn表示输入数据的大小,cn表示完成计算任务Θn所需的CPU周期总数。
1.2.1 本地计算
(2)
MD的本地计算能耗为:
(3)
其中,η表示每个CPU周期消耗能量的系数,设置η=10-26是根据文献[18]中的方法获得。
1.2.2 边缘计算

(4)
(5)
对于许多应用程序而言,计算结果的大小通常远小于输入数据的大小,因此忽略了服务器将计算结果发送给设备的开销[19]。根据上面分析,将计算模型定义为:
(6)
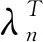
2 基于博弈论的功率优化卸载算法
2.1 问题描述
博弈论作为一种有效的方法被广泛应用于解决目标约束的多博弈参与者之间的决策问题[20]。在多个参与者的博弈中,每一步都有一个理性的参与者对前一步中其他参与者的行为做出反应,并进行局部最优决策。经过若干步骤后,这些参与者自组织形成一个相互满意的解决方案。
本文提出基于博弈论的功率优化卸载方案,采用博弈论解决多用户卸载决策问题,结合二分搜索法优化传输功率来降低传输时延和能耗,从而最小化系统的计算开销。根据第1节的系统模型,将最小化系统计算开销问题建模为:
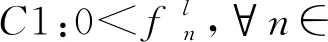


(7)
其中,C1保证分配给用户的本地计算能力为正,C2保证分配给卸载用户的计算资源不超过服务器所拥有的最大资源fs,C3保证分配给用户的传输功率为正且不大于最大传输功率,C4用户选择相同信道进行卸载时的干扰不超过预先设定的阈值。
在式(7)中,需要优化的变量是传输功率与用户卸载决策,由于功率pn为连续变量,卸载决策a为整数变量,因此该问题被制定为MINLP。为了能够求解式(7),进一步将其分解为两个相关的子问题,首先优化传输功率pn,用于特定的卸载决策;然后在上一步的基础上优化用户的卸载决策a,从而最小化系统计算开销。基于此,可重写MINLP问题式(7)为:
s.t.C1,C2,C3 andC4
(8)
式(8)中的功率优化和卸载决策的约束是相互解耦的。因此,该问题可以重写为:
s.t.C2,C3 andC4
(9)
其中,Z(a)是MD进行卸载决策时的最佳传输功率。
2.2 优化传输功率
结合式(4)和式(5),将式(9)重写为:
s.t.C2,C3 andC4
(10)
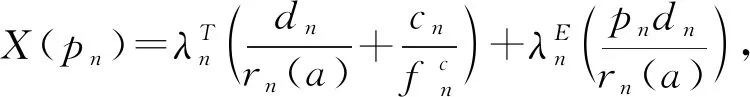
(11)
从式(11)可以看出,当χ(pn)达到最小值时C(pn)为最优。但是χ(pn)的二阶导数在定义域内并不总是正的,因此,χ(pn)在定义域内不是凸的。
引理1χ(pn)函数是单峰的。
证明首先χ(pn)在R是二次可微的,接下来检查拟凸二阶条件,存在一点x0既满足χ′(x0)=0也满足χ″(x0)≥0。
χ(pn)的一阶导数为:
(12)
χ(pn)的二阶导数为:
(13)
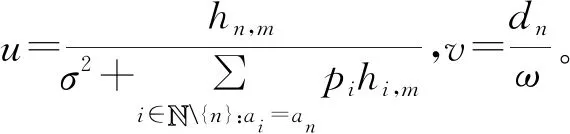
(14)
将式(14)计算出的pn替换到式(13)中,得:
(15)

1.Initialize p0、ζth、ξ;
2.if φ(p0)<0 then
4.else
5.Initialize pl=0 and ph=p0;
6.pz=(pl+ph)/2;
7.if φ(pz)<0 then
8.pl=pz;
9.else
10.ph=pz;
11.until ph-pl<ξ
13.end if
2.3 优化卸载策略

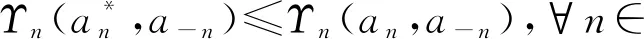
定理1博弈Λ至少有一个纯策略NEP。


(16)
其中,om表示用户选择的信道,Πl和Πc(r)分别为:
(17)
(18)

(19)

(20)
借用势函数Φ来证明博弈Λ至少有一个纯策略NEP,根据势函数的定义,即式(16)、式(17)和式(18)可得用户n在计算卸载决策变化前后的势函数为:
(21)
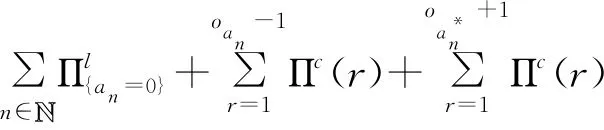
(22)
其中,oan表示卸载的用户,由式(19)~式(22)可得:
(23)
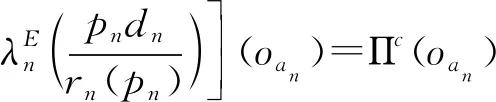
(24)
(25)
同理,根据势函数的定义,即式(16)~式(18)可得用户n在计算卸载决策变化前后的势函数为:
(26)
(27)
同样,根据式(24)~式(27)可以得出:
(28)
对于情况3):和情况2)类似,很容易证明得出:
通过上述3种情况的证明,势博弈可以通过一个精确的势函数表示,并且根据纳什均衡存在定理[20],其中至少存在一组纯策略纳什均衡。多用户卸载作为一个有限博弈,也会得到这样一组策略,并达到纳什均衡。根据上面分析,本文提出的基于博弈论的功率优化算法(Game-Theoretic with Power Optimization Offloading Algorithm,GT-POOA)详细描述如下(ε为GT-POOA收敛的迭代次数):

输出A*、Υn

4.store MD n into set of A*
5.end for
6.while A*=∅ do

9.else
10.an=an
12.end while
3 仿真结果与分析
本节通过仿真来验证GT-POOA的性能,模拟一个多用户MEC计算卸载系统,表1为性能评估中的主要参数设置,并将GT-POOA与以下卸载方案相比较:
1)博弈论卸载方案(GT-scheme):单纯的博弈卸载。
2)多用户计算卸载(MECO):一种自适应顺序卸载博弈方法。
3)本地处理(Computing locally at the ME):所有的用户总是本地执行任务。
4)计算卸载(Computing offloading at the edge):所有用户将任务进行卸载。
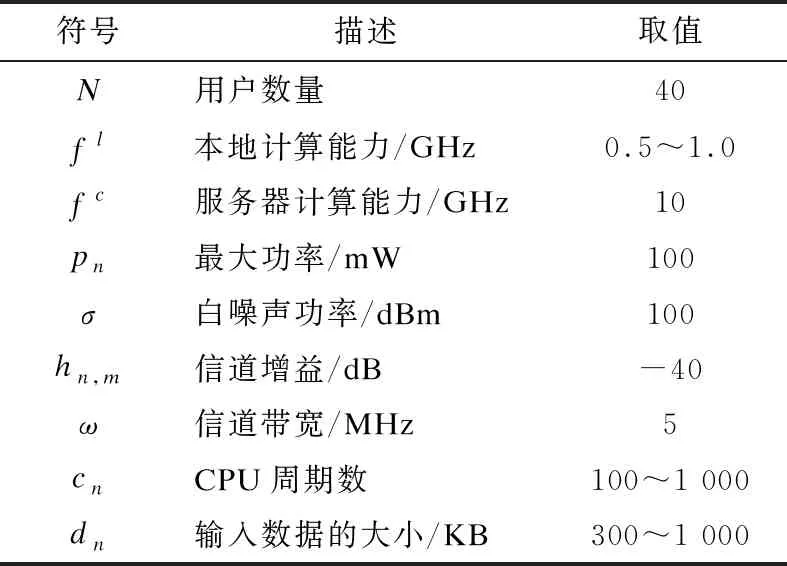
表1 仿真参数
首先验证GT-POOA的纳什均衡性和收敛性。分别进行多次重复实验(N取20、30、40),通过图2可以看出,GT-POOA在经过有限次迭代后可以达到纳什均衡。通过图3可以看出,GT-POOA在MDs逐步增多的情况下,收敛的平均迭代次数与MDs的数量是近似线性的。
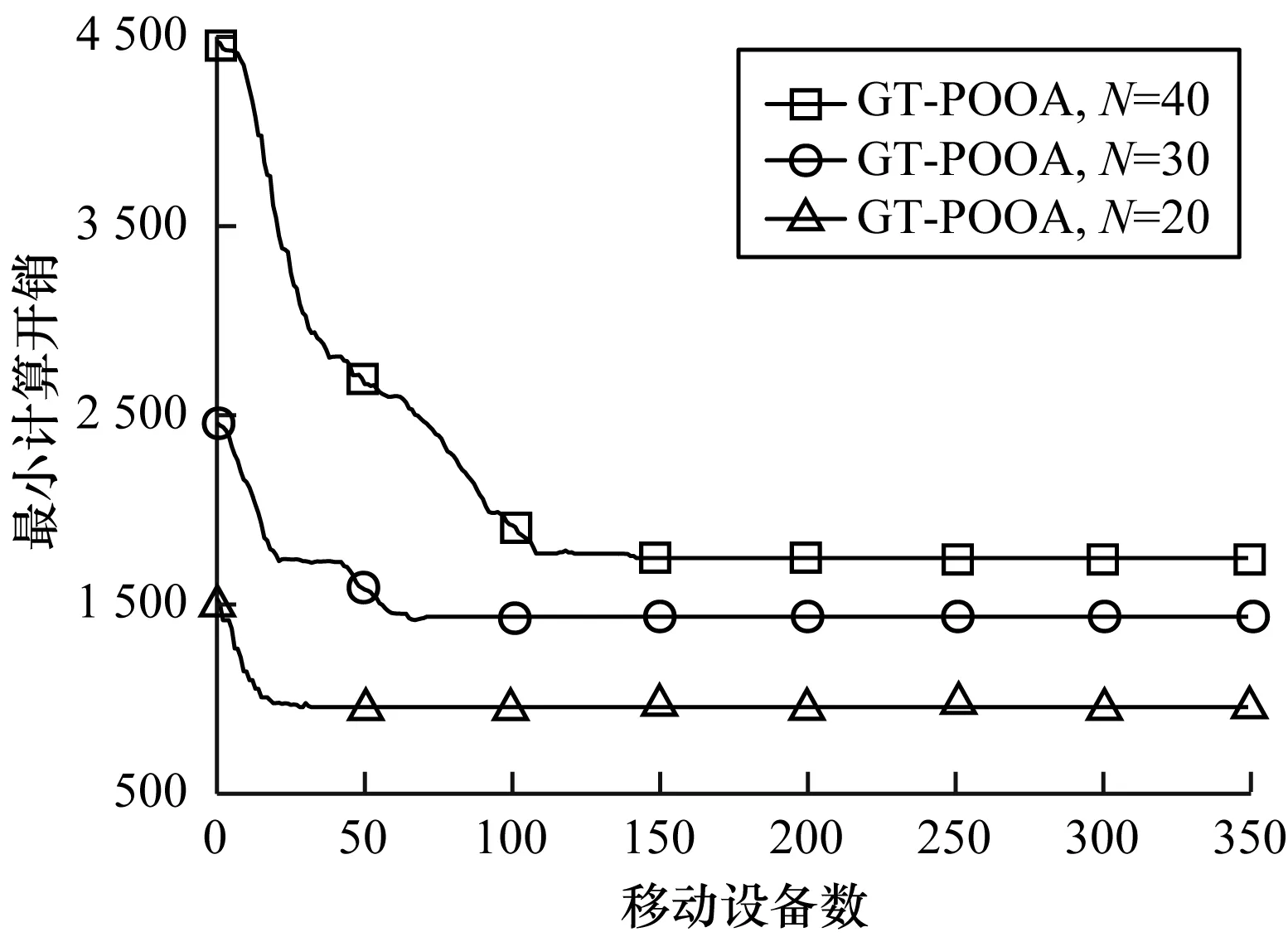
图2 GT-POOA在最小计算开销下的收敛性
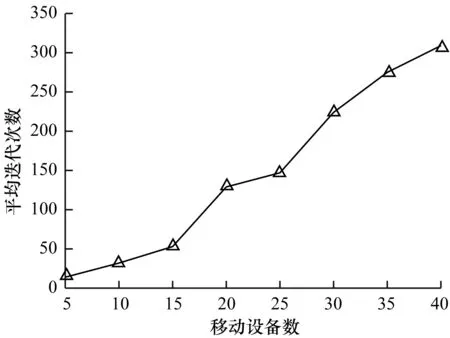
图3 不同用户数下GT-POOA收敛的平均迭代次数
本文通过实验来研究用户在不同卸载方案下的平均边缘计算用户的数量和平均系统计算开销(N分别取10、15、20、25、30、35、40)。从图4可以看出,对于有益于边缘计算用户数量的度量,本文提出的GT-POOA与上述卸载方案1)、方案2)、方案4)相比,性能分别可以提高15%、8%、31.5%。从图5可以看出,与上述卸载方案1)~方案4)相比,本文方案性能可以提高41%、12%、67%、71.8%。本文利用二分搜索算法为卸载用户找到最佳传输功率来减少传输时延和能耗,并采用博弈论为用户组找到最佳的卸载决策组合来降低系统成本。综上分析,本文提出的GT-POOA算法具有较好的计算卸载性能。
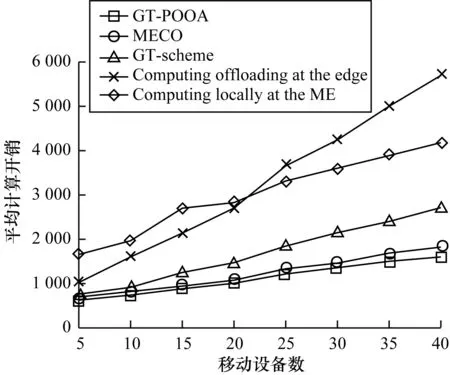
图5 用户在不同卸载方案下的平均计算开销
4 结束语
本文采用博弈论解决MEC中多用户之间的计算卸载决策问题,设计一种基于博弈论的功率分配算法GT-POOA,以实现多用户计算卸载博弈的纳什均衡。仿真结果表明,GT-POOA具有较好的计算卸载性能。下一步将研究用户在动态计算和离开状态下的MECO场景,从而实现更有效的计算卸载机制。
