具有势场启发因子的蚁群路径规划仿真

王 辉， 于立君， 胡羽坤， 王莹莹

（哈尔滨工程大学自动化学院，哈尔滨150001）

0 引 言

移动机器人路径规划指在存在障碍物的环境中寻找一条从起点到终点的无碰撞的路径［1-3］。大量的算法被应用于机器人的路径规划之中，如人工势场法［4，5］、遗传算法［6，7］、粒子群算法及蚁群算法［8-10］等，每一种算法各有优劣。

蚂蚁系统（Ant System，AS）是由M. Dorigo 于20世纪90 年代提出的一类仿生算法，算法开始被成功应用于旅行商问题（Traveling Salesman Problem，TSP）等组合优化问题，之后也被用来解决移动机器人路径规划问题［11-13］。文献［14］中提出了最大、最小蚂蚁系统（MAX-MIN Ant System，MMAS），将信息素限制在一个区间内，有效避免了搜索过程中的早熟现象。文献［15］中提出了基于蚁群遗传算法的移动机器人路径规划方案，该方案能够减小蚁群算法搜索初期的盲目性，提高搜索效率，在具有较强的全局搜索能力和鲁棒性等优点的同时，也存在搜索效率低且容易陷入局部最优的缺陷。

针对蚁群算法存在收敛速度慢及复杂环境下收敛差的问题，本文提出了一种改进的势场蚁群算法，引入势场启发因子，并控制整个搜索过程的不同阶段两种算法的重要程度，快速找到从起始点到目标点的无碰撞路径。

1 蚁群算法基本模型

蚂蚁会在走过的路上泼洒信息素，而这种信息素又会影响后续的蚂蚁对路径选择，蚂蚁趋向选择信息素浓度高的路径这种正反馈机制使得蚂蚁可以发现长度短的路径。

在t 时刻，蚂蚁k 从节点i 到节点j 转移的概率为：

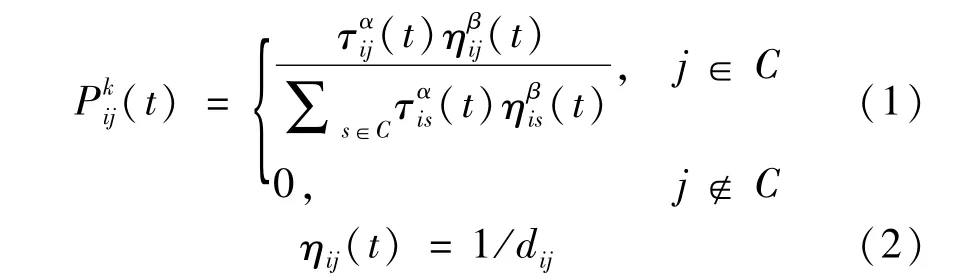
式中：Pkij为蚂蚁k从节点i到节点j的转移概率；dij为节点i和节点j之间的距离；ηij为启发因子，表示蚂蚁从节点i转移到节点j的期望程度；C为蚂蚁下一步可选择节点的集合；S 为节点变量；τij为节点i 与节点j之间的信息素浓度；α 为信息素浓度τij在求取转移概率时所占的比例；β为启发因子ηij在计算转移概率时所占的比例。

信息素的改变有两种方式，随着时间流逝会有一部分信息素挥发掉，蚂蚁走过的路径会释放一部分信息素。待全部蚂蚁都到达目标位置或完成轨迹搜索后信息素的更新策略为：

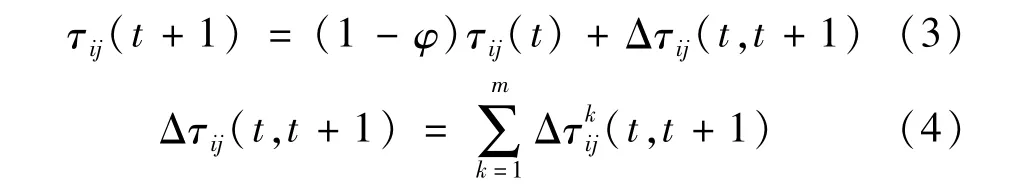
式中：Δτkij（t，t ＋1）为第k 只蚂蚁在时刻（t，t ＋1）留在路径（i，j）上的信息量；Δτij（t，t ＋1）为一次迭代完成后，轨迹（i，j）上的信息素增量；φ为信息素衰减系数，防止信息素无限累积。Δτkij（t，t ＋1）的更新存在3 种模型，分别为蚁密模型、蚁量模型和蚁周模型。文献［16，17］中通过实验对比3 种模型的效果，表明蚁周模型在机器人路径规划方面优于其余两种，该模型为：

式中：Lk为第k只蚂蚁完成搜索形成路径的总长度；Q为信息素强度系数。

选择最大、最小蚂蚁系统算法，最大、最小蚁群算法是将信息素浓度控制在一个范围内，即ηij∈［min，max］，将不在此范围内的信息素强制设置为min 或max，设置方法为：当ηij＜min 时，令ηij＝min，当ηij＞max时，令ηij＝max，最大、最小蚂蚁系统可以有效防止蚂蚁陷入局部最优路径。

2 人工势场法的改进

2.1 人工势场算法分析

人工势场法是一种虚拟力法。通过目标位置产生的引力势场和障碍物产生的斥力势场的叠加控制移动机器人的运动，搜索一条无碰撞的路径。

引力势函数：

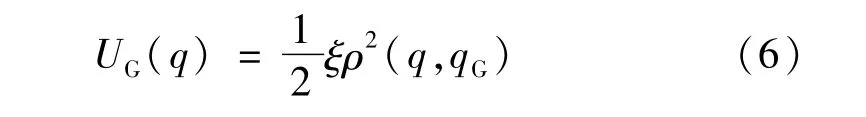
式中：ρ（q，qG）为移动机器人的当前与目标的距离；ξ为尺度因子。

目标点对机器人的引力为目标势函数的负梯度，即：

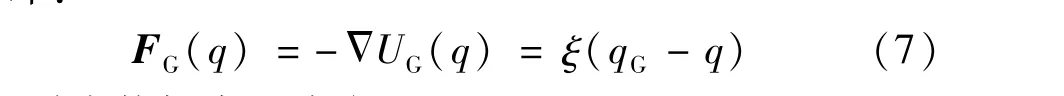
斥力势场表达式为

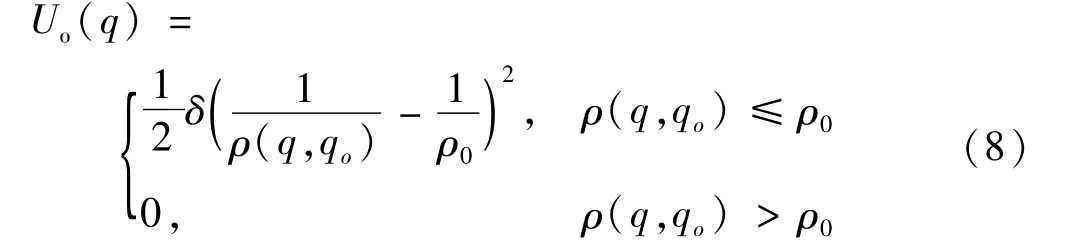
式中：δ为斥力尺度因子，ρ（q，qo）是机器人距离障碍物的最短距离，ρ0是障碍物的影响半径。则障碍物对机器人的斥力：Δ

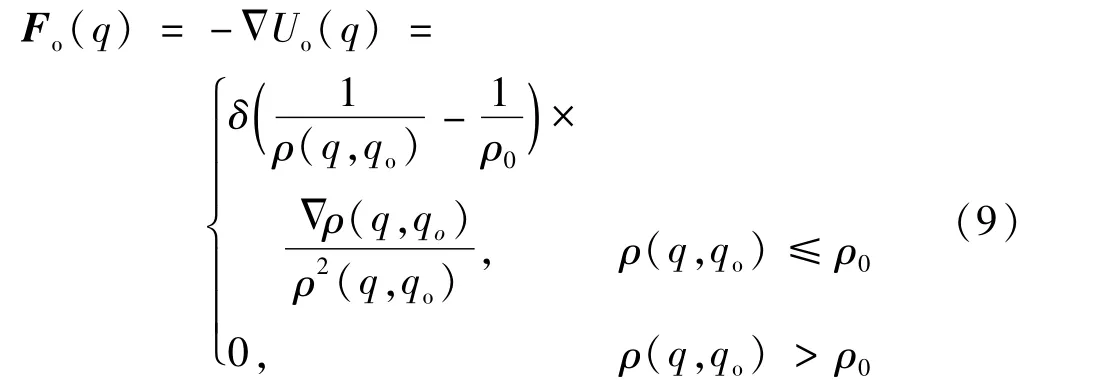
机器人受到的合力为引力和斥力之和，即：

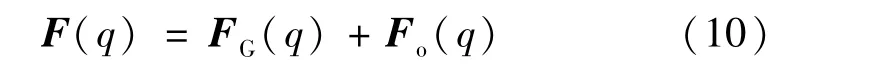
人工势场法以其数学计算上的简单明了被广泛应用，但是也存在很多缺陷，比如目标不可达和在障碍物附近振动的问题。

2.2 人工势场算法的改进

为防止机器人距离障碍物距离过远时引力大造成容易与障碍物碰撞的问题，对引力函数进行改进，设置一个阈值dmax，当机器人与障碍物之间的距离小于dmax时，引力势场为二次函数形式，当机器人与障碍物距离大于或等于阈值dmax时，引力势场为距离的一次函数。

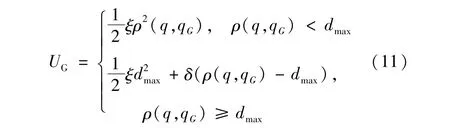
则目标点对机器人的引力函数：

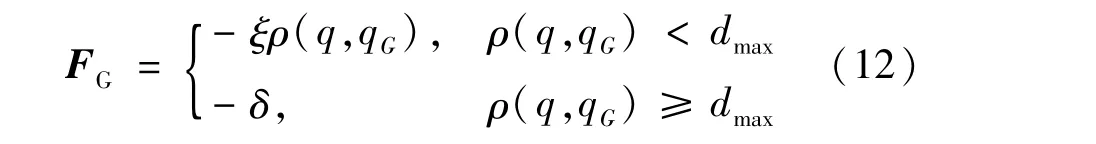
对于机器人在障碍物附近振动的问题，对斥力函数进行改进。障碍物对机器人产生的斥力场为：

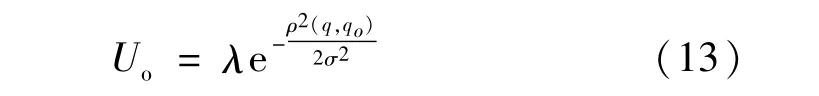
式中：λ是正比例系数。

由此得出障碍物对机器人的斥力

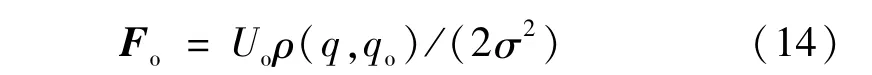
改进前后的人工势场法在障碍物附近的振荡情况分别如图1、2 所示，图中左上角为起始点，右下角为目标点。

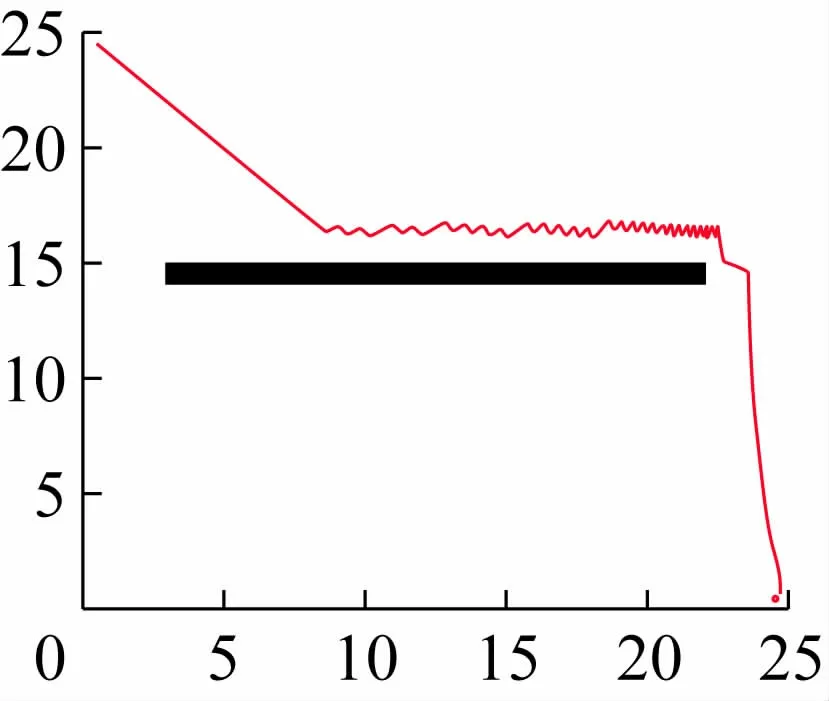
图1 未改进人工势场法路径图

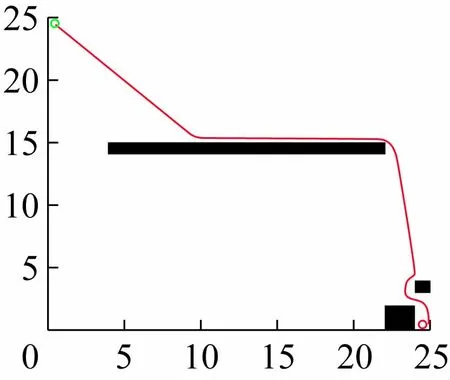
图2 改进人工势场法路径图

经过改进的人工势场算法解决了障碍物附近抖动的问题和目标附近有障碍物导致的目标不可达问题，但还存在易陷入局部最小点的问题（见图3），本文中的蚁群算法可以弥补人工势场法在这个问题上的缺陷。

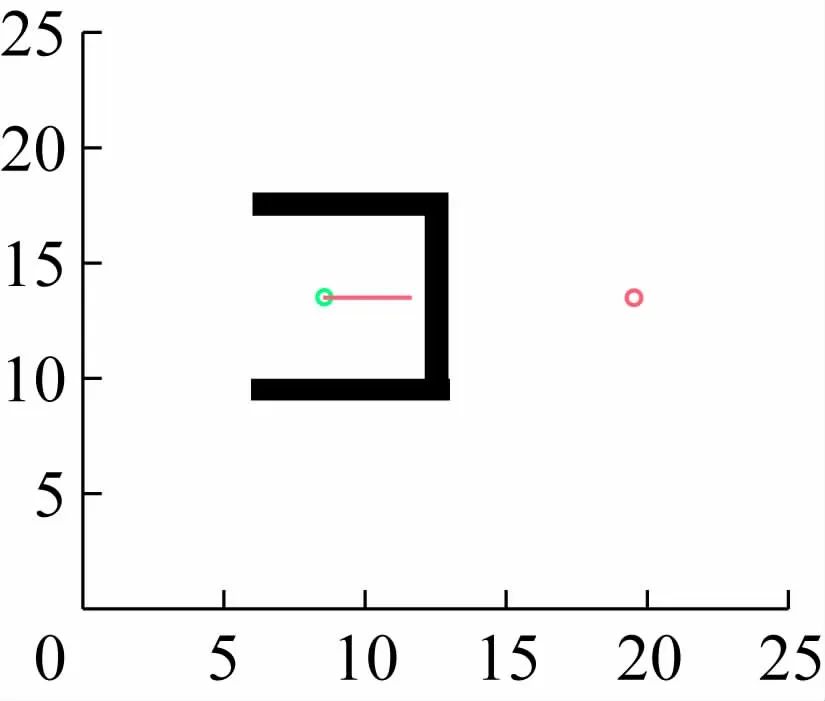
图3 人工势场法陷入极值点

3 势场蚁群算法

蚁群算法在搜索初期由于信息素均匀分布使得蚁群算法花费的搜索时间长。针对这一情形，使用人工势场法对蚁群算法进行改进。改进如下：将人工势场的势场力信息作为蚁群算法的启发信息，蚁群算法的概率转移表达式修改为

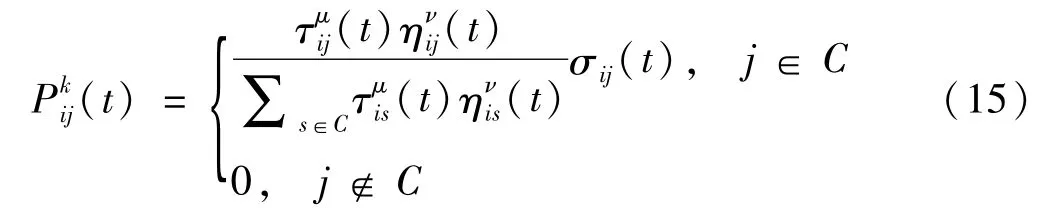
式中：μ ＝α；ν ＝β；γ 为人工势场法在方向选择上占的比重；σij为根据人工势场法计算出的8 个方向的选择概率，规定和势场合力F 夹角最小的方向的选择概率为

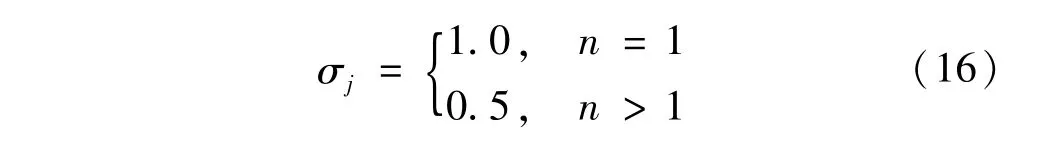
当n ＞1 时，选择其余方向的概率为

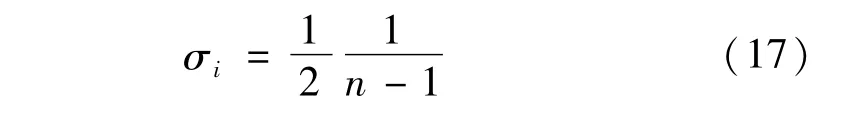
式中：n为蚂蚁下一步可以选择的方向的个数。图4给出了蚂蚁可能会遇到的一种环境情形，a、b、c、d、e、f为下一步可以选择的方向及各个方向选择概率值。

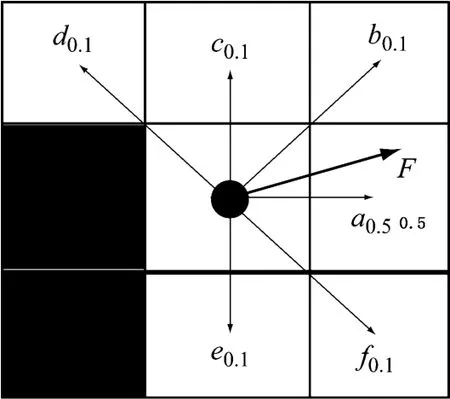
图4 蚂蚁下一步选择概率分布图

对于普通的实验环境，使用式（15）总能快速找到一条最优或次优的无碰撞道路，但是对于特殊的实验环境，如图3 则可能出现失败的情况，因为在这种环境中人工势场法失效，此时要去除人工势场算法的影响，即将式（15）中的参数γ 设置为0，此时改进的算法变成了单纯的蚁群算法。为了使算法能够适应各种环境，将算法进行以下修改。

设置算法的循环次数LoopMax，循环次数阈值LoopFlag，当前循环次数为Loop，当LoopFlag ＜Loop时，使用式（15）计算转移概率，当LoopFlag≥Loop 时，令γ等于0，即单纯的蚁群算法。在算法开始的时候使用单纯的蚁群算法找到起点到目标点的路径，这时信息素会出现差异，这些信息会被后续蚂蚁使用，解决了特殊环境下机器人找不到路径的问题。

程序的流程如图5 所示，其中：

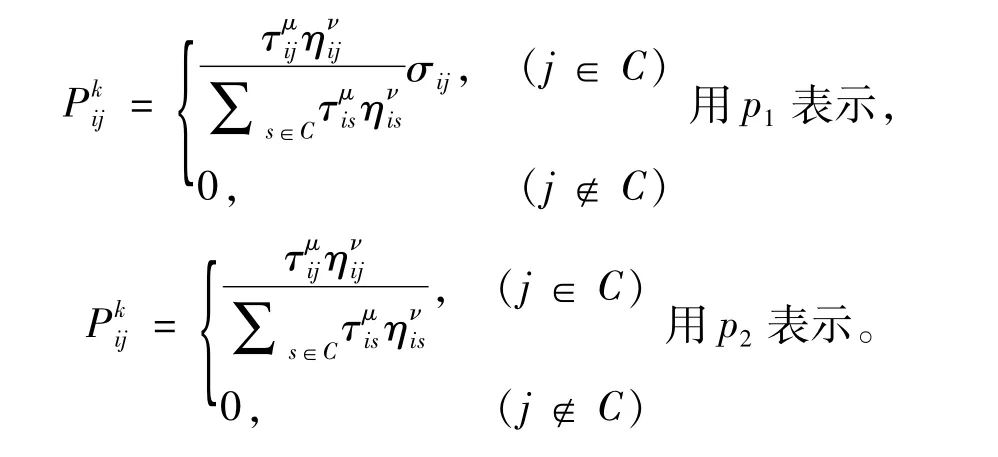
4 仿真分析

机器人活动的环境设置为25 ×25 的栅格区域，当障碍物不足一个栅格时用一个栅格表示，栅格的边长为1，机器人必须在这个栅格区域内寻找到从起点到目标点的无碰撞路径。

采用几个不同的环境进行仿真实验，进行10 次的独立仿真实验，数据取平均值，路径图为随机选取的一次生成路径。实验对比了未改进的蚁群算法和改进之后的算法的路径长度和程序运行时间两项，表1 为未改进的算法生成的路径数据，表2 为改进后的算法生成的路径数据。仿真实验使用环境地图如图6、8 ～10所示。

由表1 和表2 的数据可见，改进前、后的算法和改进前的算法相比较能够寻找到最优的路径，而且在平均路径长度上有稍微的改善，平均运行时间有明显的改善。

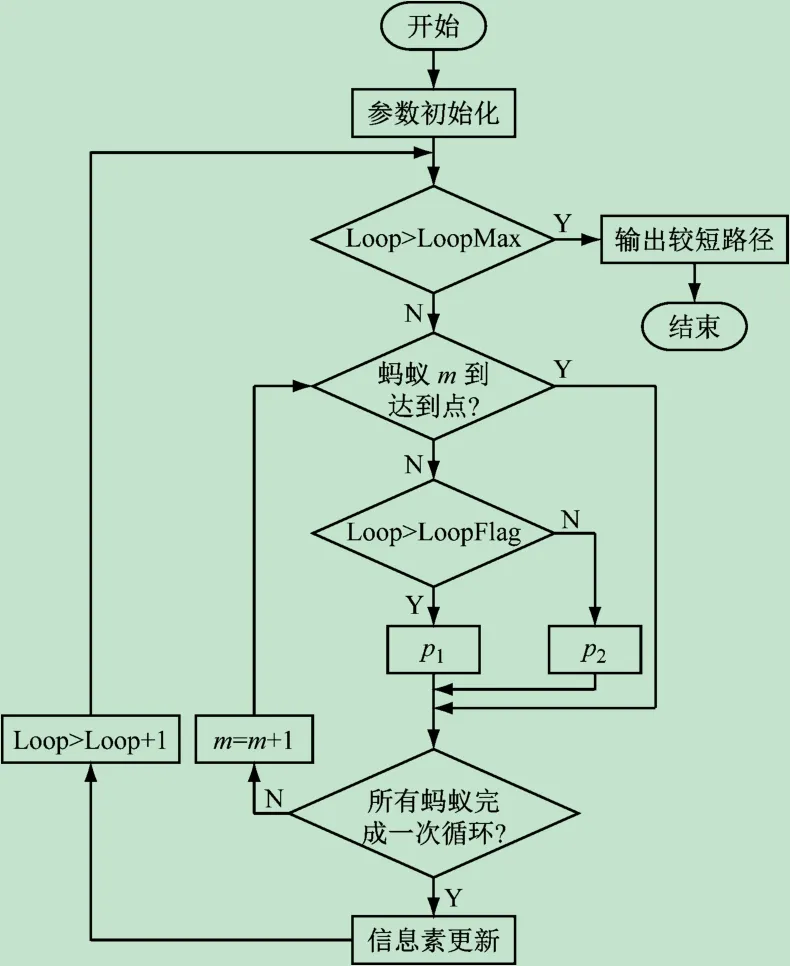
图5 程序流程图

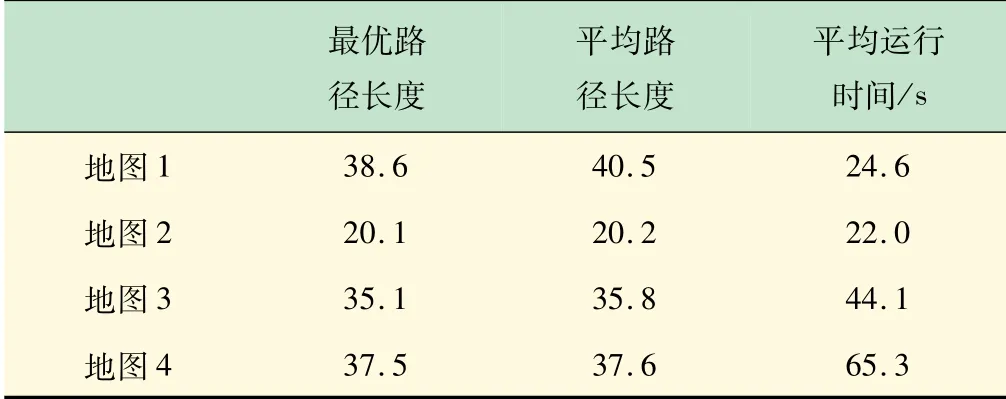
表1 未改进算法生成的路径数据

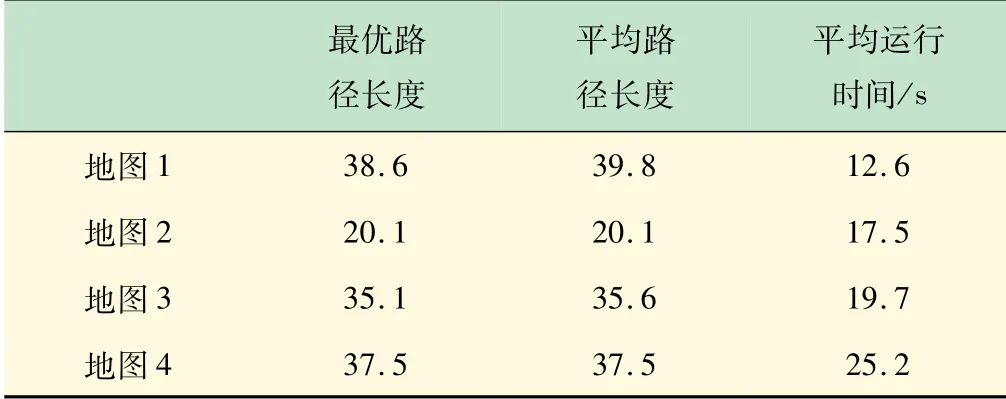
表2 改进后算法生成的路径数据

图6 仿真环境地图1

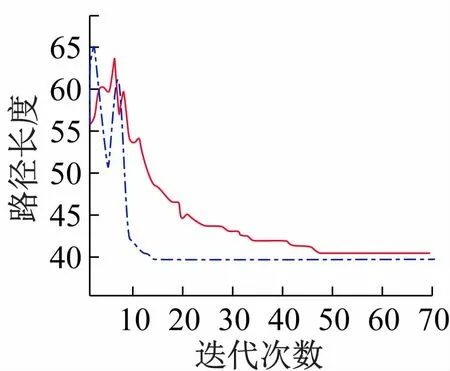
图7 地图1改进前后的路径收敛曲线对比图

图7 为地图1 改进前、后的路径收敛曲线对比图，其中蓝色点划线为地图1 改进之后的收敛曲线，红色线为未改进的蚁群算法的收敛曲线，图11 为地图4 改进后的路径收敛曲线图，可见，改进之后的算法收敛的速度明显加快。

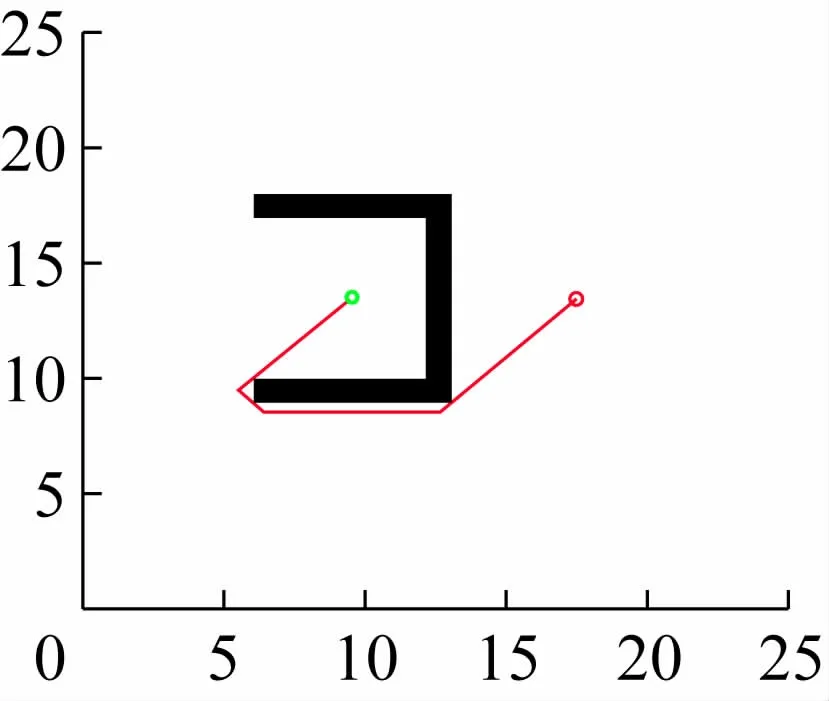
图8 仿真环境地图2

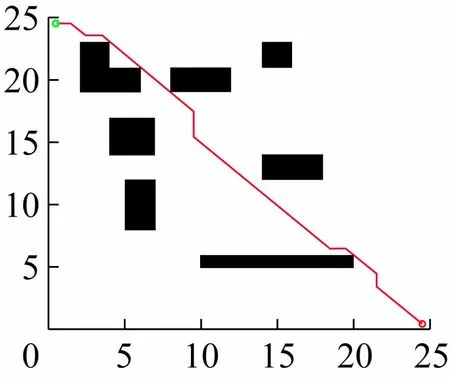
图9 仿真环境地图3

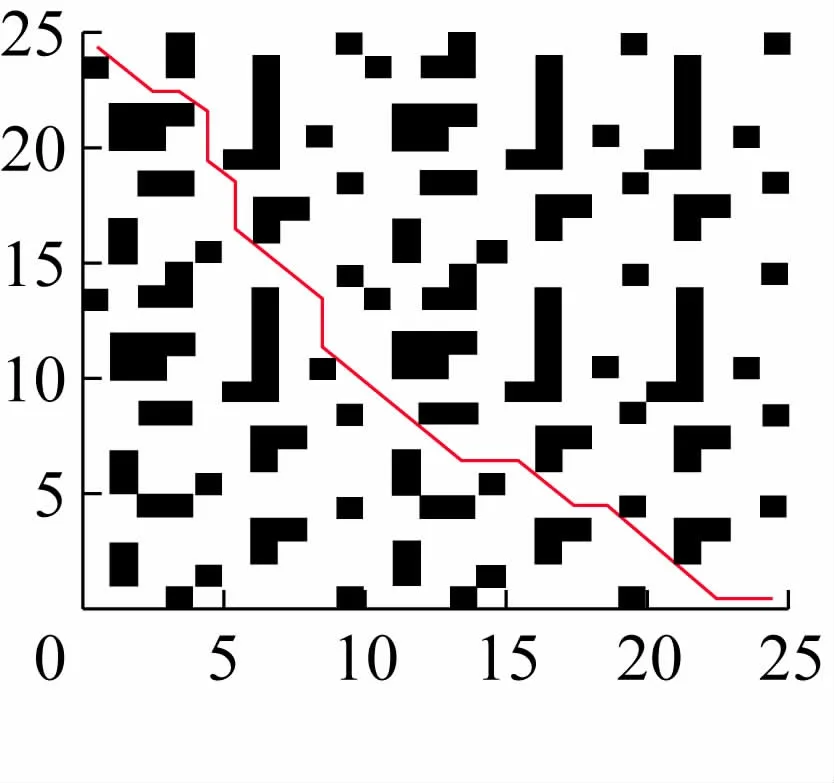
图10 仿真环境地图4

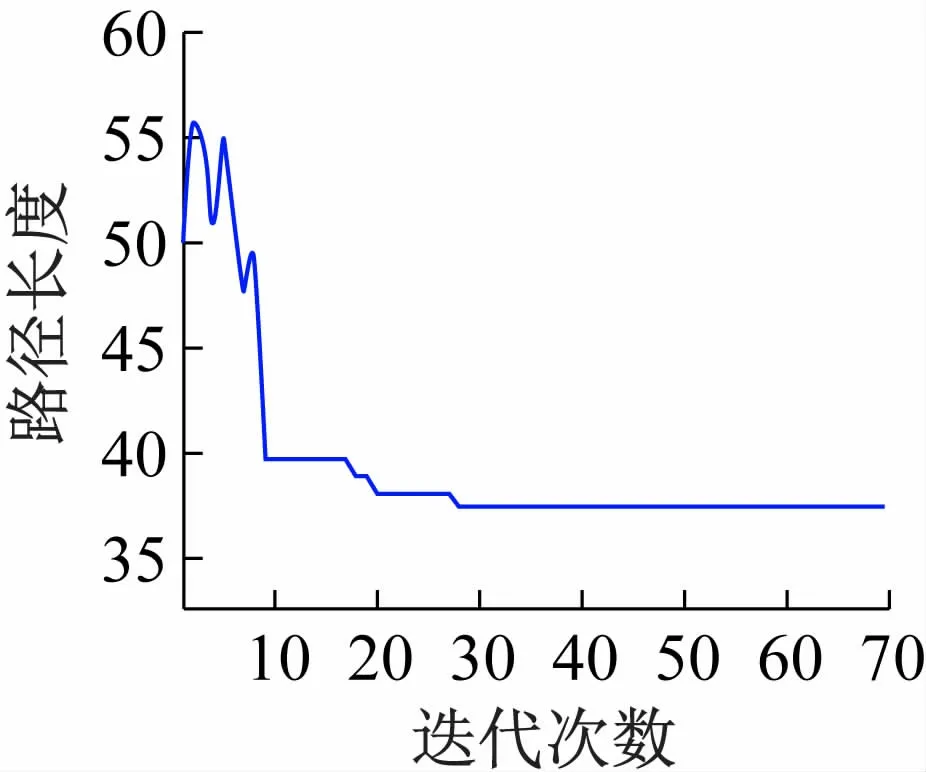
图11 地图4 改进后的路径收敛曲线图

5 结 语

本文首先对人工势场算法进行改进，提出引力势场采用分段函数的方法来解决人工势场法造成的一些问题，如机器人在障碍物附近抖动问题、机器人和目标点距离过大时容易和障碍物发生碰撞的问题，并定义了势场启发因子。将改进后的算法嵌入蚁群路径规划算法中，在找到最优或次优路径的基础上，提高了蚁群算法的收敛速度，实验室环境下的仿真实验证明了改进方法的合理性。学生通过仿真平台对移动机器人路径算法进行仿真对比分析，大大提高了学生实验兴趣。