柔性机器人动力学跟踪变阻抗控制

张 刚， 布 挺， 焦文潭， 王 波

（1.洛阳理工学院电气工程与自动化学院，河南洛阳471000；2.河南省嵌入式技术应用工程技术研究中心，河南洛阳471003；3.河南省嵌入式技术应用工程研究中心，河南洛阳471000）

0 引 言

随着机器人行业发展，机器人逐渐由简单的搬运、码垛等行业转换为更高精度，与人协作的应用场景渗透。为适应机器人与交互的环境，越来越多的厂商专注于将机器人轻量化、小型化。医疗、教育、娱乐等领域使用机器人需要机器人具有更轻的质量，更加健全的安全保护措施，随之而来的是手臂必须通过交叉部件进行物理连接，由于机构减速较小，本体刚度不够等问题，导致频繁的机械振动［1］。机构的柔性主要分为杆件柔性及关节柔性，相当于为整个机器人控制系统引入了新的自由度，机械臂的控制更加复杂，难以整定；同时，柔性机器人具有功重比高的特性，能耗远小于传统机器人［2］，响应速度快和操作空间大，更适应当前机器人研究界重视人机协作的大环境［3］。

在打磨等具有环境力感知的应用中，同时进入到与人接触或协作的场合中，机器人的力控制或柔顺控制是核心的技术问题［4］。阻抗控制是一种间接的力控制方法，其不直接对期望的位置和力进行控制，而是通过调节机器人末端的阻抗来实现机器人的柔顺控制［5-6］。常用的阻抗关系为刚度、阻尼和惯量系统。阻抗控制与力/位置混合控制相比具有离线任务规划量小，不需要控制模式切换、稳定性更高等优点，因而得到了广泛的应用。

本文依靠动力学的控制策略，通过调整目标阻抗参数使机器人适应环境，规划机器人末端的运行轨迹，使得机器人末端轨迹跟踪过程更加平顺，在不牺牲速度的同时可使得机构的冲击磨损更小，更加适用于柔性多关节机器人。

1 动力学建模

图1 所示为本文研究的柔性机器人本体，由于机器人作业任务的描述往往在笛卡尔空间，将机器人动力学方程转换到笛卡尔空间并设计阻抗控制器，其主要特点是机器人可以快速、准确地移动到指定位置，控制精度高［7］。

图1 柔性机器人本体

机器人本体的动力学分析主流的方法有拉格朗日法、牛顿-欧拉法、高斯法、凯恩法、旋量（偶数）法和罗伯逊维滕贝格法［8］。

1.1 牛顿欧拉法建模

牛顿欧拉方程是递推的形式，计算过程如下：

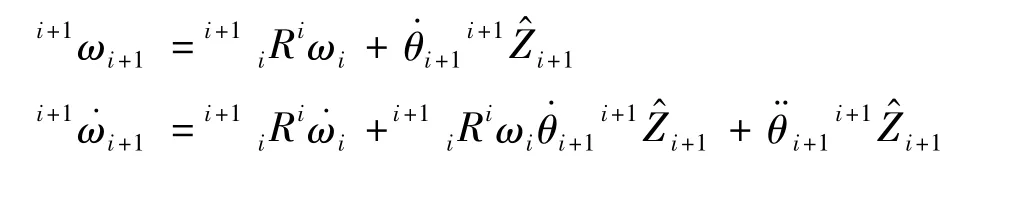
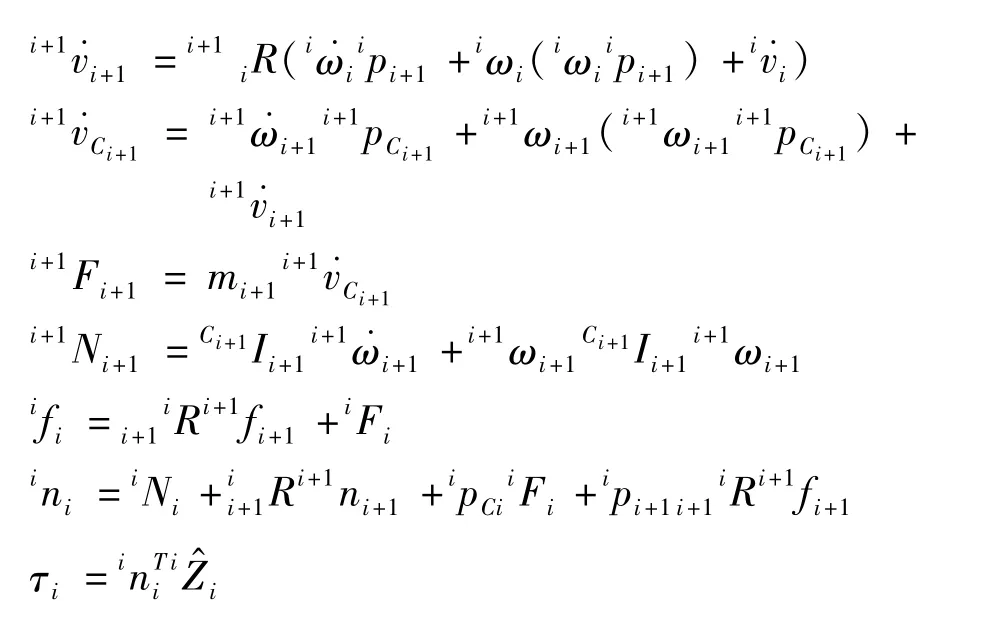
其中：iωi为第i个连杆的角速度在坐标系｛i｝中的表示·i表示第i个关节的旋转引起的角速度，对于串联机器人，iωi是θ·i和上一个关节速速iωi-1的合成；i＋1iR是3 ×3 维的姿态阵，是坐标系｛i｝相对坐标系｛i ＋1｝的姿态矩阵；i＋1˙vi＋1是坐标系｛i ＋1｝的原点加速度在坐标系｛i ＋1｝的表示；i＋1˙vCi＋1是第i ＋1 个连杆质心的加速度在坐标系｛i ＋1｝的表示；i＋1Fi＋1是第i ＋1 个连杆质心处由加速度引起的力在坐标系｛i ＋1｝的表示；mi＋1表示第i ＋1 个连杆的质量；Ci＋1Ii＋1是第i ＋1 个连杆相对于第i ＋1 质心坐标系的惯量矩阵；ifi是第i 个质心处受力，是加速度产生的力和后一个连杆传递力的合成；ini表示坐标系｛i｝原点处的扭矩，是3 ×1 维的扭矩；τi是ini在Z 轴方向的分量，也是关节i 处所需的扭矩值。

1.2 惯性力项

系统的速度传递雅可比矩阵可表示为：

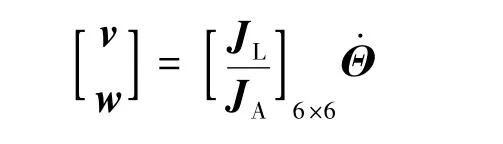
系统动能表达式为：

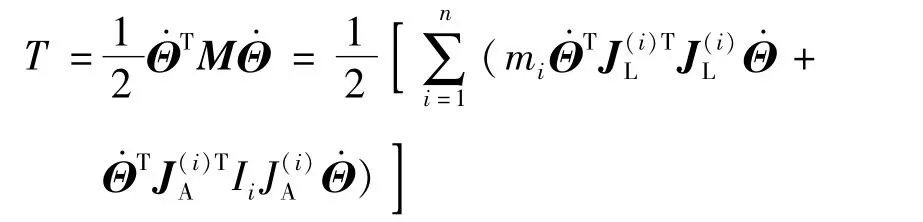
由此可得质量阵：

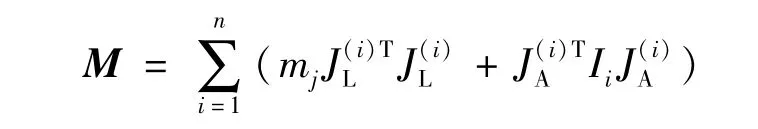
其中：J（Li）、J（Ai）分别为质心雅可比矩阵的线速度和角速度对应项。

1.3 重力项、离心力和哥氏力项

机械手总的重力势能为：

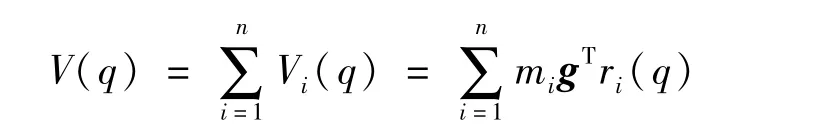
其中：g是机器人基坐标系的重力向量；V（q）与关节变量q相关，而与关节速度˙q无关。重力项：

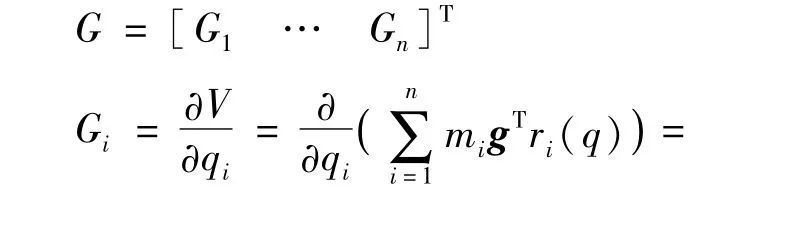
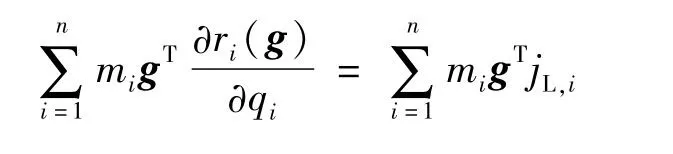
按Chiristoffell符号法，离心力和哥氏力项的C矩阵可由M矩阵求得：

故在求出M后代入Chiristoffell公式，可得C矩阵。

1.4 摩擦模型

由于摩擦对柔性关节机器人的低速和低刚度阻抗控制性能影响很大，构建了一种基本的摩擦力模型来提高机器人动力学特性［9］。动态摩擦补偿不仅提高了位置和力跟踪性能，还保证了系统的稳定性。加入摩擦力模型的动力学建模下的位置控制明显改善了柔性关节系统的位置精度和扭矩振动［10-12］。此外，通过摩擦补偿也提高了阻抗控制的力跟踪能力。完整的动力学模型表达式为：

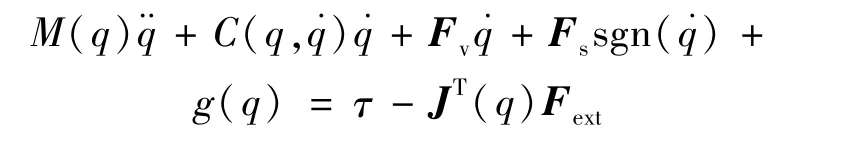
其中：Fv∈Rn×n和Fs∈Rn×n为黏性摩擦和静摩擦系数对角矩阵；向量sgn（˙q）∈Rn×1为关节速度的符号函数。机器人的联合传动摩擦模型由黏性摩擦力和恒定的干滑动摩擦力组成。然而，根据库仑定律，干摩擦力线性地取决于由变速器驱动的负载，对于在有效载荷的大变化或惯性力和重力下工作的机器人，必须考虑到这一点。此外，对于低速启动的机器人，必须考虑Stribeck效应。第1 步，为每个关节识别摩擦模型参数，一次移动一个关节（该步骤已经过验证）；第2 步，这些值在动态模型中固定，用于识别所有机器人惯性和重力参数。对于这两个步骤，识别连接在机器人跟踪具有不同有效载荷的轨迹时收集的所有联合数据，以获得惯性和新摩擦参数的全局最小二乘估计。

2 阻抗控制

基于模型的控制：①力矩传感器；②Series Elastic Actuator（SEA）；③电流估计。若有基于电流估计力矩或是有力矩传感器用第1 个；若是基于六维力传感器，用第2 个。

2.1 笛卡尔空间阻抗控制

2.1.1 操作空间动力学方程

阻抗控制的目的是在机器人运动和外部转矩之间实现一种特殊的期望动力学关系［13］。为了研究机器人末端点的阻抗控制，假设施加于机器人末端点的外力为Fext，关节空间机器人的动力学方程为：

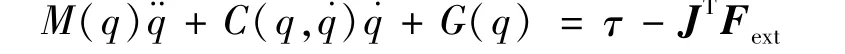
首先，两面都乘以雅可比矩阵转置的逆，得到：

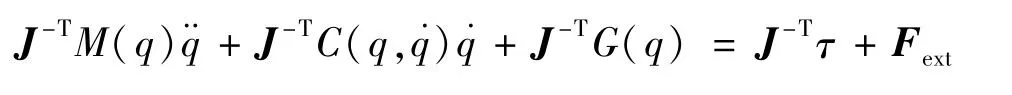
其次，求关节空间和笛卡尔空间加速度之间的关系。

由雅克比矩阵的定义可得：

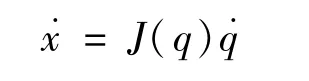
求导得到：

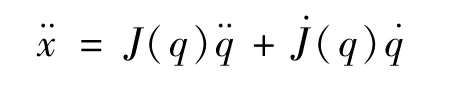
由解出关节空间的加速度得到：

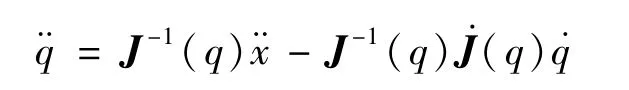
代入得：

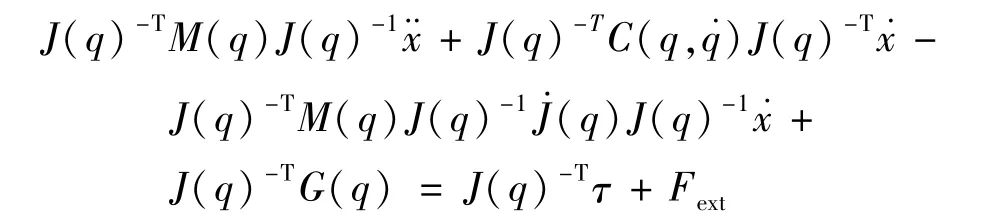
该方程可以被重写为：

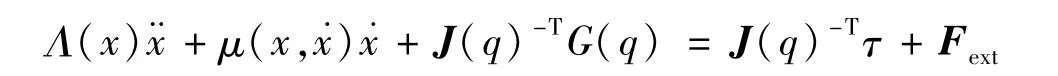
其中：各项分别为：

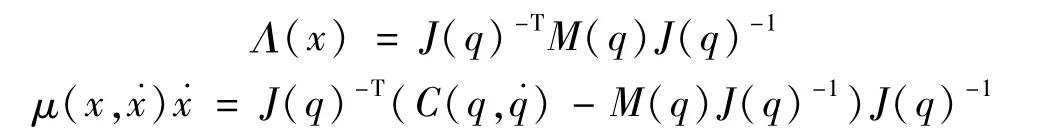
重力项和关节转矩项可以分别写为Fg（x）和FT，则系统方程可以写为：

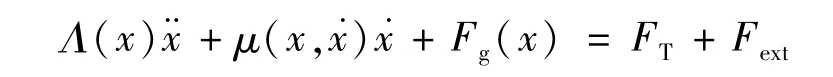
2.1.2 笛卡尔空间经典阻抗控制

为实现期待的阻抗特性，当前位置点与目标位置点的偏差被引入：

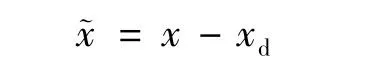
其中：xd为虚拟平衡位置点。

阻抗控制律被设计成质量-弹簧-阻尼系统形式：

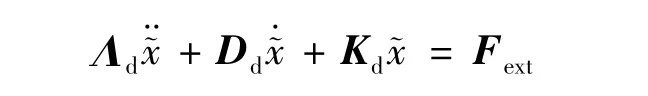
其中：Kd、Dd、Λd分别为刚性、阻尼、惯量的正定矩阵。在大部分机器人应用中，该控制律形式足以描述机器人的阻抗控制特性。当期待刚性、阻尼、惯量矩阵都是正定矩阵时，系统具有渐进稳定性。

经典的阻抗控制律可以由方程直接计算得到，可以得到构成期待闭环系统的控制输入为：

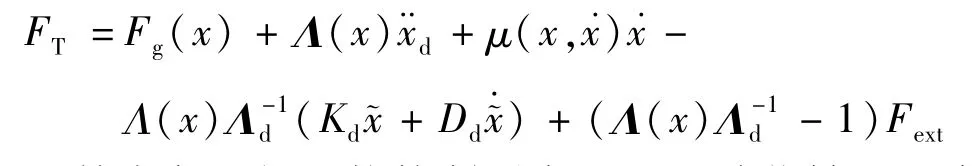
笛卡尔空间阻抗控制器实际通过关节转矩τ 实现，代入τ ＝J（q）TFT变换，得到关节转矩为：

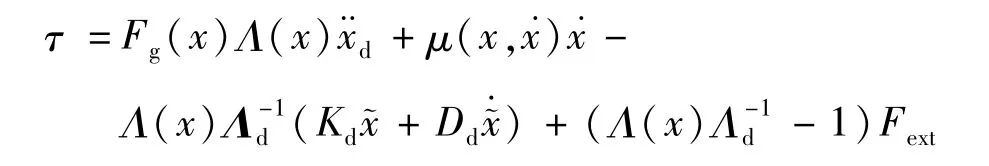
可以看出，阻抗控制的输入中包含外力Fext，Fext通常由安装在末端执行器的力／力矩传感器测量得到，当不安装末端力／力矩传感器时可以通过关节转矩传感等方式间接测量Fext，但计算比较复杂且准确的不高。当期待惯量矩阵Λd与机器人的惯量矩阵Λ（x）相等时，外力反馈可以被避免：

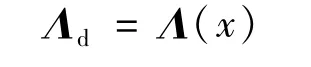
此时满足系统正则条件下的无源性条件，笛卡尔空间阻抗控制成为：

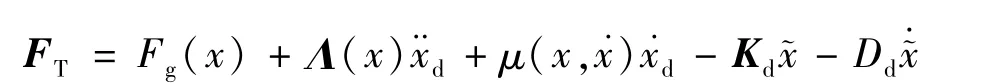
同样，当Λd＝Λ（x）时，反馈控制中的Fext项将被消掉，此时关节空间阻抗控制成为：

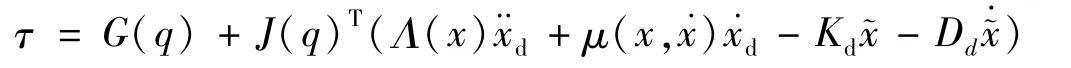
笛卡尔空间阻抗控制采用笛卡尔空间基于力的阻抗控制结构实现，采用关节转矩反馈的控制结构如图2 所示。其中外环的位置闭环与目标阻抗特性结合得到力控制量，内环为力闭环，该力闭环在关节空间实现时需要经过雅可比矩阵的变换。

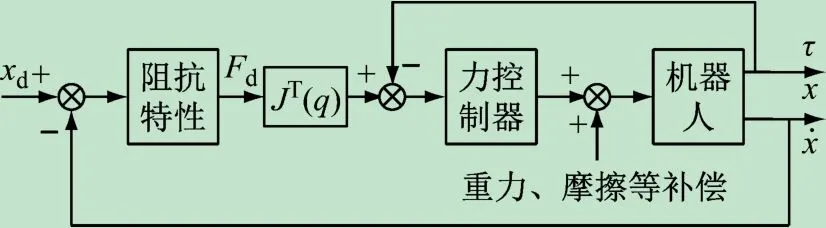
图2 笛卡尔空间基于力的阻抗控制结构图

2.2 基于无源性理论的机器人阻抗控制

如果柔性关节机器人以阻抗控制律作用于外部环境，那么机器人的动力学特性将受电动机转动惯量和机器人关节刚度的影响［14］。分析可知，电动机转子惯量越小，或者关节刚度越大，实际系统的动力学误差将越小。在机器人的控制中，通过关节转矩的反馈可以减小电动机转子的有效惯量，相应地实际系统的动力学误差将减小，系统的期望动力学行为也会更好［15］。

考虑电动机转子惯量时，机器人系统与电动机系统动力学模型为：

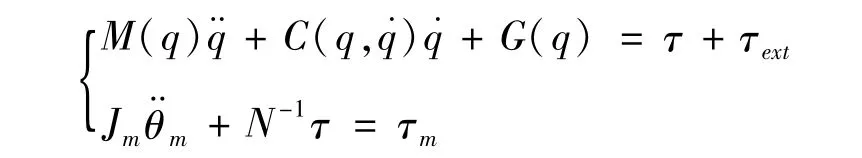
将电动机角度转换到关节，代入θm＝Nθ，变换为：

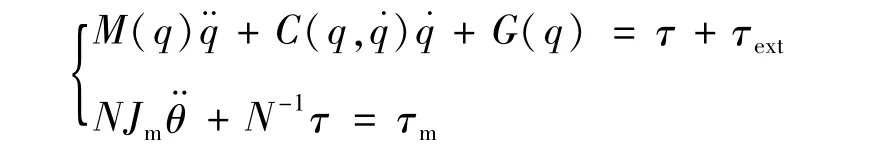
引入关节转矩反馈：

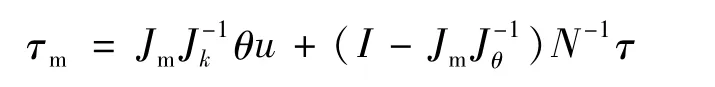
其中：u是新引入的电机控制量。通过上述反馈，得到新的系统动力学方程为：

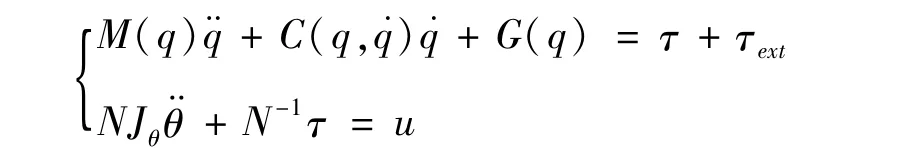
显然，和具有相同的形式，通过关节转矩反馈，电动机的有效惯量由Jm变为Jθ，关节转矩反馈的采用相当于引入了电机惯量的调整量，更小的Jθ可以得到更好的动力学跟踪性能。

根据阻抗控制的需求，新的控制输入变量u 可以被分解为两部分，一部分是应用于阻抗控制的刚度和阻尼项；另一部分作为重力补偿项，即：

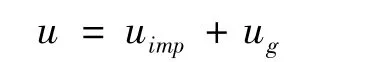
根据阻抗控制原理，阻抗控制项可以被设计成PD控制律：

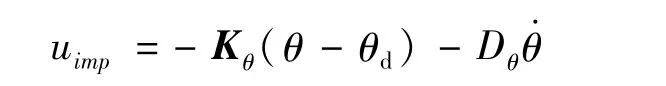
其中：Kθ为刚度矩阵；Dθ为阻尼矩阵；Qd为虚拟的期望平衡位置。而重力项可以通过动力学计算得到：

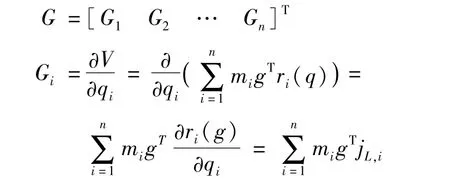
代入阻抗控制项和重力项，并考虑到关节的转矩传递关系，得到闭环系统方程为：

3 实际验证

如图3 所示，阻抗控制的效果可以从4 个测试中体现。包括：基于阻抗模型的牵引测试、基于阻抗模型的阻抗测试、基于阻抗模型的斜面力跟踪和基于自适应阻抗的力跟踪。

图3 直线轨迹拟合结果

3.1 基于阻抗模型的牵引测试

在人机系统中，阻抗控制和导纳控制方法得到了广泛的应用。阻抗控制是运动到力的动态映射，导纳控制是力到运动的动态映射。力控制流程：检测力，利用阻抗公式，然后计算出增量，发给机器人。本文实现了一种阻抗控制方案来体现阻抗模型的牵引示教，机器人与操作人员可以进行手把手的直接交互。

图4 所示为基于阻抗模型的牵引测试效果，通过实验验证了该算法的有效性。

图4 基于阻抗模型的牵引测试

3.2 基于阻抗模型的阻抗测试

利用李雅普诺夫稳定性定理，保证了柔性机器人的阻抗角结果与实际角之间的误差收敛于零。为了适应非结构化环境下的人机交互，建立了基于位置的阻抗控制系统。

图5 所示为基于阻抗模型的阻抗测试效果。针对机器人加工过程中位置的不确定性，提出了一种基于力估计模型的位置阻抗控制器。该控制策略采用模糊逻辑控制器调节阻抗参数，减少约束运动中的干扰，提高力控制效果。该模型根据末端执行器的反馈位置调整阻抗控制器的基准力，得到光滑的表面。

图5 基于阻抗模型的阻抗测试

3.3 力和位置跟踪

本文对机器人阻抗控制进行了力和位置跟踪测试，来验证算法的有效性。如图6 所示，对机器人的关节力矩进行采集，对机器人的关节位置进行采集，如图7 所示。实验证明，如果进行有效的参数调试，可以很好地利用阻抗控制进行力和位置的跟踪。本文提出的简单稳定的力跟踪阻抗控制方案，能够跟踪指定的期望力，并能补偿环境位置、刚度以及机器人动态模型中的不确定性。采用鲁棒位置控制算法对机器人动力学中的不确定性进行补偿。接触后，在力可控制的方向上，根据所要求的力、环境刚度和位置误差实现新的阻抗函数。新的阻抗函数简单稳定。分析了不同阻抗参数下的稳定性和收敛性，实现了稳定的力和位置的跟踪执行。

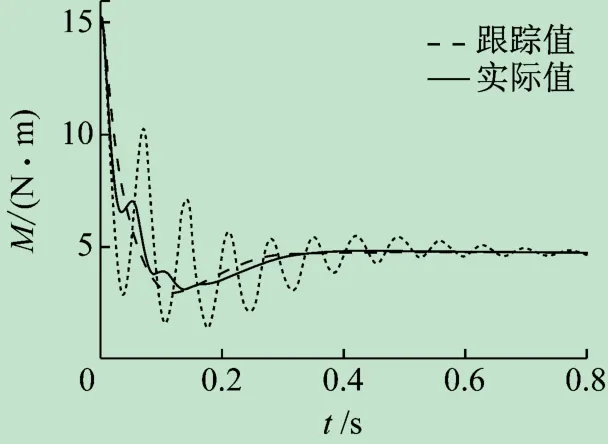
图6 阻抗控制下力跟踪实验数据

图7 阻抗控制下为位置跟踪实验数据

4 结 语

本文试图定义一种统一的操作方法，该种方法足够通用，可以在这种情况下控制操作。操纵控制的难点之一在于，虽然现有的控制理论大多适用于线性系统，但操纵本质上是一个非线性问题。阻抗和导纳的概念常被应用于线性系统中，并被人们所重视作为等价的和可互换的。机器人的控制需要在关节空间实现，基于关节转矩反馈的阻抗控制是近年来理论研究的热点。对关节空间转矩反馈的阻抗控制进行设计，要建立Lyapunov 函数进行稳定性分析。首先建立柔性机器人动力学模型，然后对惯性力、重力项、离心力、哥氏力和摩擦力进行详细的分析，再次对柔性机器人进行阻抗控制模型建立讨论了笛卡尔空间下的阻抗控制的实现。最后，进行了自由空间阻抗控制和位置阻抗控制等实验，验证所设计方法的有效性。