基于协方差矩阵重构的稳健波束形成算法
2020-06-18郭业才胡国乐
郭业才, 陈 晨, 胡国乐
(1.南京信息工程大学电子与信息工程学院,南京210044;2.江苏省大气环境与装备技术协同创新中心,南京210044;3.安徽大学电气工程与自动化学院,合肥230601)
0 引 言
波束形成作为阵列信号处理中的一个主要方面,广泛应用于雷达、声纳、通信系统以及医学影像等领域[1-2],其实质是根据阵列接收信号对各个阵元加权并进行空域滤波,增强期望信号,抑制干扰信号。标准Capon波束形成器是最为经典的波束形成算法,但在实际应用中,由于阵列接收协方差矩阵中包含期望信号,算法对导向矢量失配等非常敏感,抗干扰性能受到很大的影响[3]。
近年来,出现了很多稳健的波束形成算法。主要有:对角加载算法[4-7],实现起来较为简单,但对于不同环境下最优加载量的选择没有一个明确的标准;特征空间法[8-10],利用期望信号导向矢量在信号子空间上的投影来代替期望信号的导向矢量,能减少信号自消现象的出现,但在低信噪比时,由于子空间缠绕(信号子空间与噪声子空间不满足正交性),导致性能严重下降;最坏性能优化法[11-15],通过经验将期望信号的导向矢量约束在一个不确定集合中,继而使干扰加噪声的输出功率最小化,但在实际应用时,不确定集合的约束参数往往难以确定,影响算法的性能。之后,文献[16]中给出了干扰加噪声协方差矩阵重构法,该方法通过对期望信号方向以外的范围空间谱积分以重构干扰加噪声协方差矩阵,去除期望信号,从而提高了鲁棒性,但该方法计算量较大。文献[17-18]中通过迭代法获得空间谱以重构协方差矩阵,避免了积分计算和凸优化问题求解,提高了导向矢量失配时的输出性能,但仍然计算量较大。文献[19-21]中用干扰来波方向的大致范围代替期望信号方向以外的范围,并用求和代替积分,大大减少了计算量,但低信噪比时,性能会出现一定程度的下降。
本文提出了一种基于协方差矩阵重构的稳健波束形成算法。该算法首先利用空间谱估计以及阵列接收信号的稀疏性,对期望信号和干扰的大致方位区间积分估计出导向矢量,然后利用主模式抑制去除信号间由于低快拍数产生的多余相关性,以得到新的协方差矩阵,最后利用新的导向矢量以及重构的协方差矩阵代入标准Capon波束形成器得到最优权值。与其他方法相比,在没有引入复杂计算量的情况下,在低快拍数与低信噪比时,本文的方法能取得一定的性能提升。
1 阵列信号模型
考虑一个阵元间距为d 的N 阵元均匀线阵(ULA),假设一个角度为θ0的期望信号和P -1 个角度分别θi(i =1,2,…,P -1)的干扰信号入射到线阵上,各信号均为窄带信号,阵元噪声为理想的平稳高斯白噪声。为了确保不过载,信源数P需小于阵元数N。经采样,第k个快拍时的阵列接收信号表示为

式中:a(θ0)表示期望信号的导向矢量;a(θi)表示干扰信号的导向矢量;s0(k)和si(k)分别表示第k 个快拍时期望信号与干扰信号的复包络;L表示快拍数;n(k)表示加性噪声。
阵列接收信号的协方差矩阵为

式中:Rs表示期望信号加干扰的协方差矩阵;σ2n表示噪声功率;阵列流形a(θP-1)];阵列接收数据表示矩阵转置运算;(·)H表示矩阵共轭转置运算。
阵列接收信号的协方差矩阵可用有限次快拍数的采样数据协方差矩阵来近似,即

波束形成器的输出为

标准Capon波束形成器又称最小方差无畸变响应(Minimum Variance Distortionless Response,MVDR),该方法在已知阵列结构的前提下先估计期望信号的导向矢量(θ0),然后利用最大信干噪比准则得到最优权值,
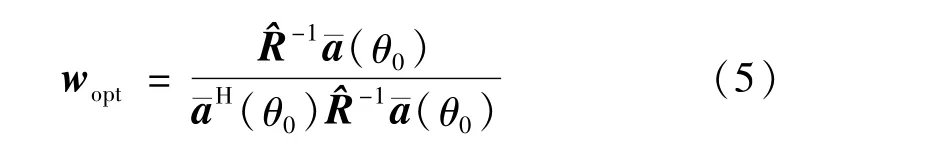
在实际应用中,由于快拍数不足,阵列协方差矩阵中包括期望信号以及期望信号导向矢量估计不准确等问题的影响,Capon 波束形成器的抗干扰性能会急剧下降,波束方向图会发生畸变。
2 基于协方差矩阵重构的波束形成算法
2.1 导向矢量估计
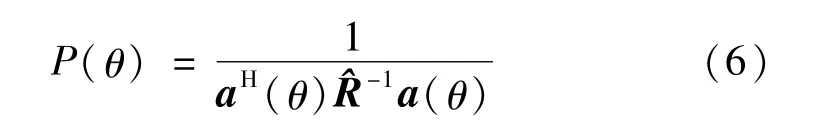
式中:a(θ)是角度为θ 的导向矢量。为了计算出期望信号以及干扰信号的导向矢量,预先使用一些低复杂度的方法。例如,由MUSIC算法等获得期望信号以及干扰信号来波的大致方向,必然会存在角度误差,但足以推断出来波方向的范围。
假设Θi表示估计的第i 个信源的来波方向范围(i =0,1,…P-1)。由于阵列接收信号在空间范围内具有稀疏性,第i 个信源的空间谱主要分布在其估计方向的邻域中,在其他方向几乎没有,所以第i个信源的协方差矩阵估计为
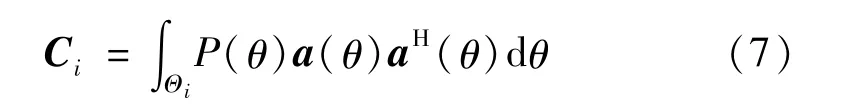
式中的积分结果难以直接获得。为了减少计算量,将积分转化为求和。将积分区域Θi等间隔划分为K点,则求和式为

对协方差矩阵进行特征分解,得:
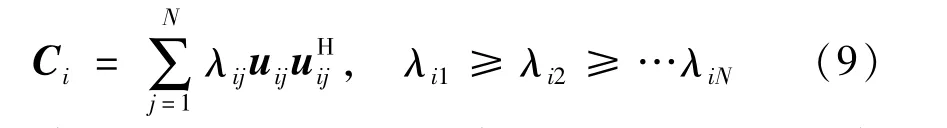
式中:λij代表Ci分解后的特征值,按从大到小的顺序排列;uij代表与之对应的特征矢量。根据子空间理论,协方差矩阵特征分解后,大特征值对应的特征矢量张成的信号子空间包含了信号的导向矢量。所以取Ci特征分解后最大特征值对应的特征矢量作为导向矢量,同时结合理想情况下导向矢量的范数限制则第i个信源的导向矢量估计为
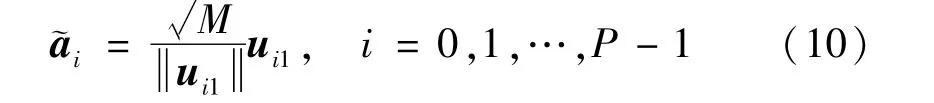
显然,在Θi范围内包含来波方向的前提下,当Θi的范围越小时,冗余信息越少,得到的协方差矩阵误差越小。
2.2 干扰加噪声协方差矩阵重构
在重构干扰加噪声协方差矩阵之前,利用主模式抑制去除信号间由于快拍数不足所产生的相关性[22],由式(2)得:

式(11)为超定方程组,Rs为未知量,利用伪逆求得其最小二乘解为

式中:A的伪逆为A+=(AHA)-1AH;Rs为期望信号加干扰的协方差矩阵,当信号间没有相关性时,Rs应当只有主对角线上有元素,这些元素代表着信号功率。但是,由于快拍数限制,信号间可能会产生多余的相关性,这些因素都会导致波束形成器的抗干扰性能下降。舍弃Rs主对角线以外的元素得到新的对角阵Rd即可去除信号间的相干性。


3 仿真与性能分析
为了验证本文算法的性能,进行仿真实验研究,并与对角加载算法、最差性能最优法、文献[16]以及文献[19]的算法进行比较。每次实验进行100 次蒙特卡罗仿真。考虑一个阵元数为10 的均匀线阵,阵元间距为半波长。远场窄带信号源包括一个期望信号和两个干扰信号,期望信号与干扰之间统计无关,阵元噪声为复高斯白噪声。期望信号的真实来波方向为3°,估计来波方向为0,角度区域Θ0=[0-5°,0+5°];两个干扰信号的真实来波方向分别为-20°和40°;估计来波方向为1和2,角度区域分别为:Θ1=[1-5°,角度区域的采样点数K根据区间内每0.1°划分一个采样点来设置。两个干扰信号的干噪比(Interference to Noise Ratio,INR)均为30 dB。其中,对角加载算法的加载量取噪声功率的10 倍,最差性能最优法的参数设置参见文献[10]。
3.1 无误时性能仿真
考虑无导向矢量失配以及阵列结构都准确已知,即信号真实来波方向与估计来波方向一致时,本文算法的输出性能。图1(a)为快拍数L =30 时,算法输出信干噪比(Signal to Interference plus Noise Ratio,SINR)随输入信噪比(Signal to Noise Ratio,SNR)的变化曲线。图1(b)为输入SNR =20 dB 时,算法输出SINR随快拍数L的变化曲线。

图1 无误差时性能
图1 表明,在不存在误差时,本文算法与文献[19]中理论最优值几乎完全一致,对角加载与最差性能最优法在高SNR时性能都会有所下降,但随着快拍数增加,会有一定程度的提升,而在动态调节各种SNR 情况下的对角加载量仍然可以获得较好的输出性能。但是在低快拍数时,对角加载与最差性能最优法的性能严重下降,这是由于小特征值扰动以及信号之间会产生多余的相关性引起的。
3.2 存在导向矢量失配时稳健性能仿真
考虑在导向矢量分别出现小角度(3°)和大角度(8°)失配误差时,本文算法的输出性能。导向矢量出现3°误差时,期望信号的估计来波方向0设定为6°,干扰的估计来波方向1和2设定为-23°和43°。图2(a)和图2(b)分别为出现3°失配时,算法输出SINR随输入SNR和快拍数L 的变化曲线。导向矢量出现8°误差时,期望信号的估计来波方向θ^0设定为11°,角度区域Θ0改为[0-10°,0+10°]。图3(a)和图3(b)分别为出现8°失配时,算法输出SINR随输入SNR和快拍数L的变化曲线。
图2 和图3 表明,随着导向矢量失配程度的增大,各算法的输出性能都会有不同程度的下降。由于文献[16、19]中的算法使用了协方差矩阵重构法去除了阵列接收协方差矩阵中的期望信号,所以在高信噪比时不会受到太大的影响。在低信噪比时,本文算法输出SINR与文献[16]接近,都优于其他算法。在高信噪比时,本文算法性能又比文献[16]好。总体而言,本文算法在出现导向矢量失配时优于其他算法。
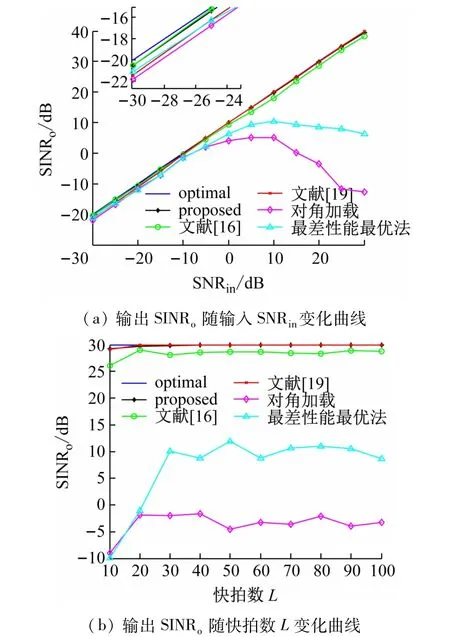
图2 导向矢量3°失配时稳健性能
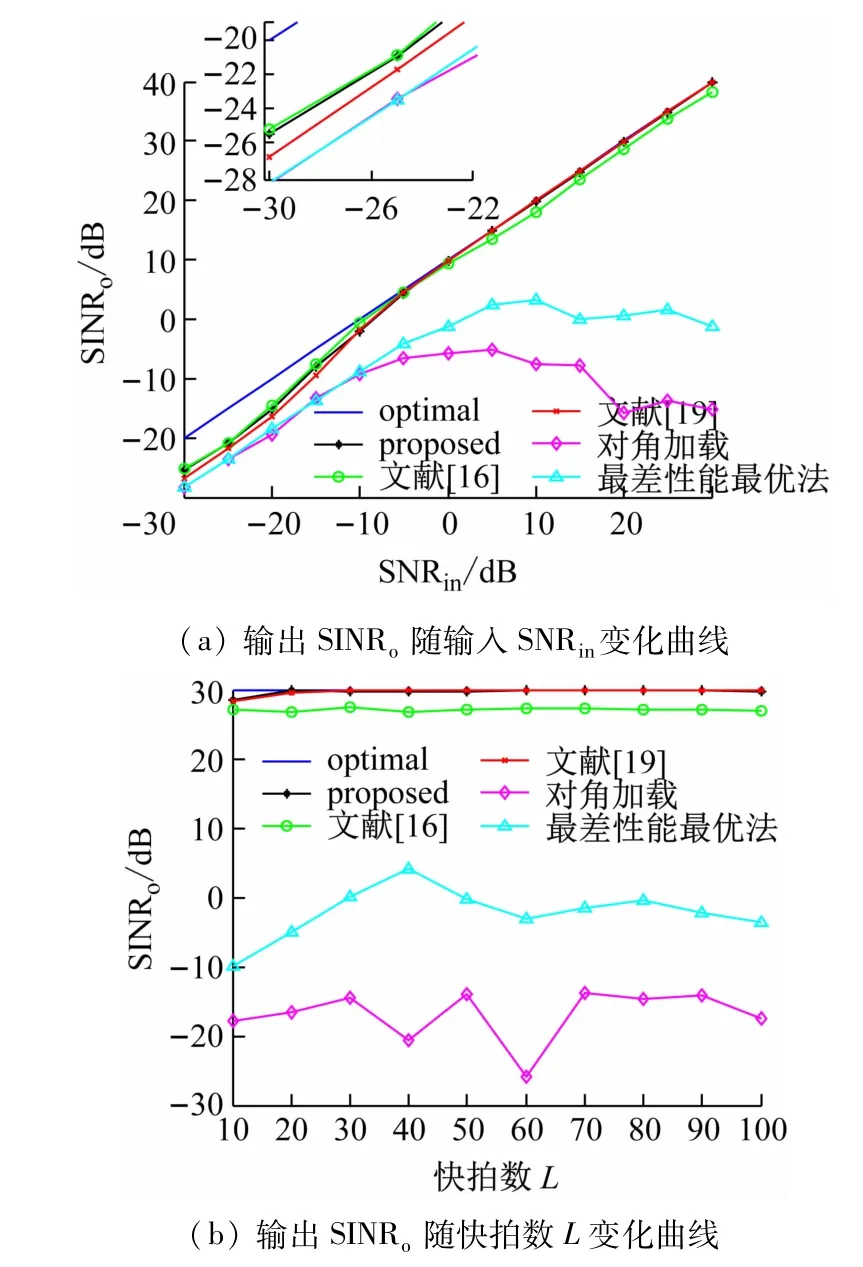
图3 导向矢量8°失配时稳健性能
3.3 同时存在导向矢量失配和相干局部散射时稳健性能仿真
考虑同时出现导向矢量3°失配误差和相干局部散射时,本文算法的输出性能,假设出现相干局部散射时的导向矢量表示为
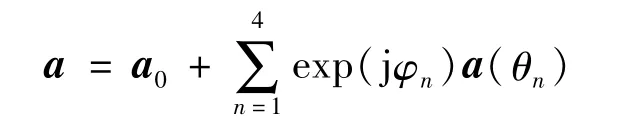
其中:a0为直达信号的导向矢量;a(θn)表示从θn方向入射的相干散射信号;φn是直达信号与相干散射信号之间相位差。相干散射信号的入射方向服从均值为0°,标准差为2°的高斯随机分布,相位差φn服从[0,2π]间的均匀分布。图4(a)和图4(b)分别为同时存在导向矢量失配和相干局部散射时时,算法输出SINR随输入SNR和快拍数L的变化曲线。
图4 表明,基于协方差矩阵重构算法的性能仍然优于其他算法,本文的算法性能总体仍是最优的,此时对角加载算法的性能也获得了提升,应该是对角加载量刚好符合要求。此外,在低快拍数时,本文算法由于去除了信号间多余的相干性,输出SINR 高于其他算法,进一步提高了算法的稳健性能。
4 结 语
本文提出了一种基于干扰加噪声协方差矩阵重构的稳健波束形成算法。该算法利用空间谱积分估计出期望信号以及干扰的导向矢量,通过主模式抑制去除了信号间多余的相干性,并对协方差矩阵进行重构,最终得到自适应波束形成的最优权值。仿真实验表明,在存在期望信号导向矢量失配误差和局部相干散射时,本算法都具有更好的稳健性,在不同输入SNR、不同快拍数时,输出SINR更接近理论最优值。
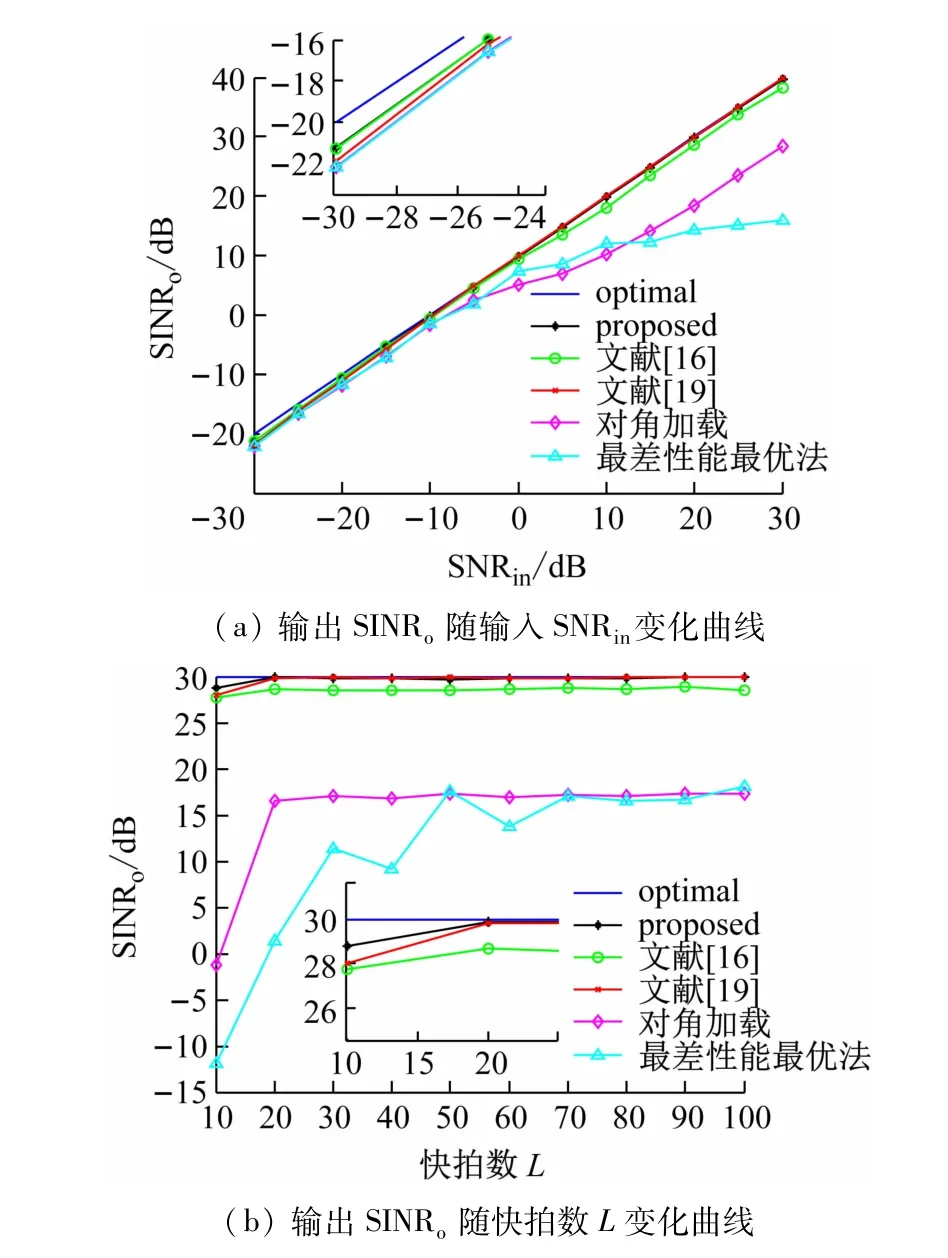
图4 同时存在失配和非相干局部散射时稳健性能
