一类三独立变量六重和差分不等式中未知函数的估计

陈立强，王五生

(河池学院数学与统计学院，广西 宜州，546300)

Gronwall-Bellman[1-2]在研究微分方程的解对参数的连续依赖性的论文中，提出了线面的积分不等式

其中c≥0是常数，并给出了未知函数的估计

(1)

因Gronwall-Bellman型积分不等式及其推广形式是研究微分方程、积分方程和微分-积分方程解的存在性、有界性、唯一性等定性性质的重要工具，数学工作者不断地研究它的各种推广形式[3-8]，使它的应用范围不断扩大.另一方面，随着差分方程理论的发展，许多学者更关注Gronwall-Bellman型不等式的离散形式及其推广形式[9-15]，Pachpatte和Singare[16]研究了三变量和差分不等式

u(x，y，z)≤a(x)+b(y)+c(z)+

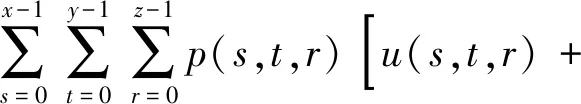
(2)

刘伟华和黄海松[17]研究了和号外具有非常数因子的三变量线性差分不等式

φ(u(x，y，z))≤a(x，y，z)+

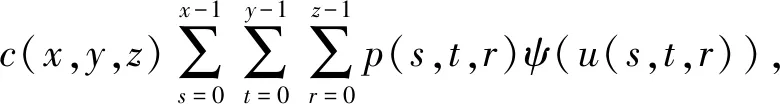
(3)

φ(u(x，y，z))≤a(x，y，z)+

(4)

本文受文献[16-17]的启发，研究了和号外具有非常数因子的三变量六重非线性和差分不等式

φ(u(x，y，z))≤a(x，y，z)+

(5)

不等式(5)把文献[16]中的线性和差分不等式(2)推广成非线性和差分不等式，把文献[17]中的三重和差分不等式(3)和(4)推广成三变量六重非线性和差分不等式.本文利用分析技巧给出了不等式(5)中未知函数的估计，最后举例说明了本文结果可以用来研究相应类型的差分方程解的性质．

1 主要结果与证明

(6)

在Ω上成立，则有函数v(x，y，z)的估计式

(7)

其中,

(8)

Φ-1是Φ的逆函数，(x1，y1，z1)∈Ω是满足

(9)

的最大自然数.

(10)

f(x，y，z).

(11)

不等式(11)中x，y保持不变，用r代替z，让r分别等于z0，z0+1，…,z-1，然后把所得到的不等式两边分别相加得到

(12)

(13)

不等式(13)中x，z保持不变，用t代替y，让t分别等于y0，y0+1，…，y-1，然后把所得到的不等式两边分别相加得到

(14)

利用引理条件Δv(x，y0，z)=0和Φ的定义,由不等式(14)可以推出

Φ(v(x+1，y，z))-Φ(v(x，y，z))=

(15)

不等式(15)中y，z保持不变，用s代替x,让s分别等于x0，x0+1，…，x-1，然后把所得到的不等式两边分别相加得到

Φ(v(x，y，z))-Φ(v(x0，y，z))≤

(16)

由不等式(16)进一步得到

v(x，y，z)≤Φ-1(Φ(v(x0，y，z))+

(17)

这就是引理要求的估计式．

定理1假设u，a，c和fi，gi(i=1，2，…，m)都是定义在Ω上的非负函数，a和c对每个变量都是单调不减的.假设φ，ψ，φ∈C(R0，R0)都是不减函数，且φ是满足φ(0)=0的严格增函数.假设L:Ω×R0→R0满足条件

0≤L(x，y，z，v)-L(x，y，z，w)≤

M(x，y，z)(v-w)，(x，y，z)∈Ω，

(18)

其中v>w≥0，M(x，y，z)≥0.如果不等式(5)成立，则有未知函数的估计式

(19)

其中,

(20)

(21)

(22)

(23)

(24)

Φ-1是Φ的逆函数，(x2，y2，z2)∈Ω是满足

Φ2(a(x2，y2，z2))+

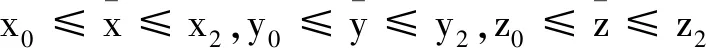
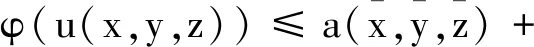
(25)

定义函数θ1如下：

(26)

u(x，y，z)≤φ-1(θ1(x，y，z))，

(27)

不等式(26)两边关x求差分得到

Δθ1x(x，y，z)=

(28)

由(28)可以看出Δθ1x(x，y0，z)=0求二阶差分Δθ1xy得到

(29)

(30)

定义函数θ2(x，y，z)如下,

θ2(x，y，z)∶=θ1(u(x，y，z))+

(31)

由上式可以看出,函数θ2(x，y，z)对于每个变量都是不减非负函数，并有

且有

(32)

对函数θ2(x，y，z)进行类似于对函数θ1(x，y，z)实施的(28)到(30)运算得到

(33)

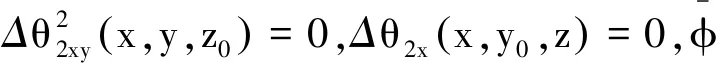
(34)

把(34)代入(30),

(35)

不等式(35)两边同除φ(φ-1(θ1(x，y，z)))得到

(36)

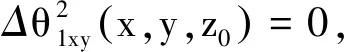
(37)

利用φ，φ，θ，由不等式(37)可以推出

Φ2(θ1(x+1，y，z))-Φ2(θ1(x，y，z))=

(38)

不等式(38)中y，z保持不变，用s代替x，让s分别等于x0，x0+1，…，x-1，然后把所得到的不等式两边分别相加得到

Φ2(θ1(x，y，z))-Φ2(θ1(x0，y，z))≤

(39)

由关系式(27)和(40),

(41)

(42)

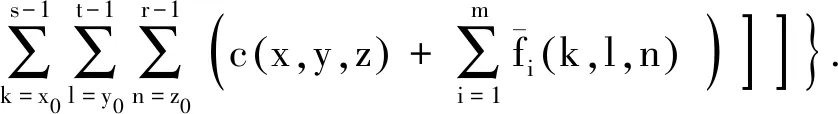
(43)

这就是定理要求的不等式(5)中未知函数u(x，y，z)的估计．

2 应用

本文结果可以用来研究相应类型的和差分方程解的性质，现在考虑具有初始条件的差分方程

(x，y，z)∈Ω，

(44)

u(x0，y，z)=e1(y，z);u(x，y0，z)=e2(x，z)，

u(x，y，z0)=e3(x，y)，

(45)

e2(x0，z)=e3(x0，y)=0，

e1(y0，z)=e3(x，y0)=0，

e1(y，z0)=e2(x，z0)=0.

(46)

推论1假设F:I×J×K×R×R→R和H:I×J×K×R→R满足下列条件:

F(x，y，z，υ(x，y，z)，h)|≤

φ(υ(x，y，z)|)(υθ(x，y，z)|+h|)，

(47)

H(x，y，z，υ(x，y，z))|≤

(48)

(49)

其中θ>0，υ|，a，φ，ψ，L，fi，gi满足定理1的要求.如果υ(x，y，z)是方程(44)满足初始条件(45)和(46)的解，那么对任意(x，y，z)∈Ωx3y3z3有方程解的模的估计式

(50)

Φ2(a(x3，y3，z3))+

证明满足初始条件(45)和(46)的差分方程(44)等价于下面的和差分方程

(x，y，z)∈Ω,

(51)

利用条件(47)～(49)，由(51)可以推出

vθ(x，y，z)|≤a(x，y，z)+

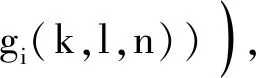
(52)

对任意(x，y，z)∈Ω成立.由于(52)具有不等式(5)的形式，利用定理1中的相应条件，就可以得到所求的方程解的模的估计式(50).