扩散风险模型中Erlang(2)间隔随机观察边界分红问题
2020-06-18王秀莲
王 伟,王秀莲
(天津师范大学数学科学学院,天津 300387)
在精算风险理论中,保险公司的盈余常用随机过程来描述.本文考虑如下扩散风险模型,盈余过程U(t)满足
U(t)=u+μt+σW(t),t≥0,
(1)
其中,u≥0是初始资金,μ>0为漂移项,通常代表保费率,σ为波动率,W(t)是标准布朗运动.假定文中随机过程都定义在一个完备的概率空间(Ω,F,{Ft},P)上.
一个常见的精算量是破产概率,即盈余值首次变为负值的概率.这一问题在该领域已经被广泛研究,如文献[1-3]等著作中均有较为详细的阐述和介绍.为了更实际的研究保险模型,De Finetti[4]提出了分红问题,即盈余过程满足某些条件时其值的一部分作为红利分掉.当前,分红问题已经变成风险理论的一个热点和中心话题,其中[5]和[6]是相关的综述性文献.分红策略有很多种类,如边界分红策略、门槛分红策略和带状分红策略等.本文将研究一类随机观察时间边界分红策略,即观察时间间隔为随机变量,在观察时刻若发现保险公司盈余超过某边界b>0,则超出部分作为红利分掉,若盈余不超过b,则不进行分红.目前已有许多论文对随机观察相关问题展开研究[7-14],其中文献 [7] 研究了复合泊松风险模型中在随机观察时间的边界分红问题,给出了计算期望折现分红函数的几种方法.最近,文献[15]里研究了模型(1)在随机观察时间间隔服从Erlang(2)分布时的最优分红问题,本文将研究该模型相应的破产问题.
设分红边界为b>0,随机观察时刻为Tk,k=1,2,…,其时间间隔Tk-Tk-1服从Erlang(2)分布,其密度函数为f(t)=γ2te-γt,t>0,其中参数γ>0.在随机观察时刻,若盈余超过b,则超过部分被作为红利分掉.红利的折现因子记为δ.令D(t)表示到t时刻的累积分红总量,且其为适应的、单调不减的左连右极过程.在该分红策略下,盈余过程Ub(t)满足方程
dUb(t)=μdt+σdW(t)-dD(t),t≥0.
(2)
设τb=inf {t≥0:Ub(t)=0}为破产时,即保险公司的盈余过程在分红策略下首次降到零的时刻.定义函数
φ(u;b)=E[e-δτbI(τb<∞)U(0)=u],
其中,I(·)为通常的示性函数.φ(u;b)是著名的Gerber-Shiu函数的一种特殊情况.为方便计算,令φ(u,i;b),i=1,2表示φ(u;b)在到下次分红时刻剩余时间分布服从Erlang(i)时的值.进一步,根据初值u与b的大小关系,记
由破产时的定义知
φL(0,1;b)=φL(0,2;b)=1.
(3)
类似文献 [15],给出如下几点假设:
1)φ′L(b,1,b)=φ′U(b,1;b),φ′L(b,2,b)=
φ′U(b,2;b);
2)φ″L(b,1,b)=φ″U(b,1;b),φ″L(b,2,b)=
φ″U(b,2;b).
1 微分方程组
定理1当0≤u (γ+δ)φL(u,2;b)+γφL(u,1;b)=0, (4) (γ+δ)φL(u,1;b)+γφL(u,2;b)=0. (5) 当u≥b时,φU(u,i;b),i=1,2满足如下的微分方程组: (γ+δ)φU(u,2;b)+γφU(u,1;b)=0, (6) (γ+δ)φU(u,1;b)+γφU(b,2;b)=0. (7) 证明当0≤u 1) 没有进行观察,概率为1-γh+o(h); 2) 进行了一次观察,概率为γh+o(h). 利用全期望公式得 φL(u,2;b)=(1-γh)e-δh· φL(u+μh+σW(h),2;b)+ γhe-δhφL(u+μh+σW(h),1;b)+o(h)= (1-γh-δh)φL(u,2;b)+μhφ′L(u,2;b)+ (8) 对(8)式进行整理,得 (γ+δ)hφL(u,2;b)+γhφL(u,1;b)+o(h). (9) (9)式两端同除以h,并令h→0可得(4)式.利用同样的方法可得(5)式. 当u≥b时,在小时间段[0,h]内考虑φU(u,2;b),有 φU(u,2;b)=(1-γh)e-δh· φU(u+μh+σW(h),2;b)+ γhe-δhφU(u+μh+σW(h),1;b)+o(h). (10) 整理(10)式可得方程(6)式. 对φU(u,1;b),由于在小时间段[0,h]内盈余超过了分红边界,注意到此时有观察即进行分红,故 φU(u,1;b)=(1-γh)e-δh· φU(u+μh+σW(h),1;b)+ γhe-δhφU(b,2;b)+o(h). (11) 利用与之前同样的方法对(11)式进行整理即得方程(7)式. 本节将利用第1节定理1所得方程组并结合假设条件1)和2)给出φL(u,i;b)与φU(u,i;b),i=1,2的显式表达. 当0≤u 即 (12) 方程(12)的根为r0>0,s0<0,r2γ>0,s2γ<0.因此φL(u,2;b)的通解表达式为 φL(u,2,b)=Aer0u+A1es0u+Ber2γu+B1es2γu. (13) 将(13)代入(4),得 Aer0u+A1es0u-Ber2γu-B1es2γu. (14) 由(3)知φL(0,1,b)=φL(0,2,b)=1,故 即A1=1-A,B1=-B.因此(13)与(14)式变为 φL(u,2;b)=Aer0u+(1-A)es0u+Ber2γu-Bes2γu, (15) φL(u,1;b)=Aer0u+(1-A)es0u-Ber2γu+Bes2γu, (16) 当u≥b时,方程(7)的通解为 其中,rγ>0,sγ<0是方程 (17) 对方程(6),由文献[15]知φU(u,2;b)的通解表达式为 Cesγ(u-b)+Duesγ(u-b). (18) 下面确定(17)式中未知系数E2与(18)式中系数C与D的关系.由(6)知 (19) 对(19)左端计算得 (20) (21) (22) 利用关系式 (22)式可变为 (23) 将(20)、(21)和(22)式代入(19)式,得 (24) 利用关系式(19),将(24)与(17)比较系数得 故 (25) 将(14)、(15)、(18)与(25)式代入假设条件1)、2)可得 (26) 为给出线性方程组(26)的解,令 h0(b)=er0b-es0b,h2γ(b)=er2γb-es2γb, (27) (28) 下面将上述所得结果归纳为如下定理. 定理2在假设1)、2)下,φU(u,i;b),i=1,2的表达式为 φL(u,1;b)=Aer0u+(1-A)es0u- Ber2γu+Bes2γu, φL(u,2;b)=Aer0u+(1-A)es0u+ Ber2γu-Bes2γu, Cesγ(u-b)+Duesγ(u-b), 其中A,B,C,D由(28)给出. 本文研究了一类扩散风险模型在随机观察下的边界分红问题.其中观察间隔时间服从Erlang(2)分布.文中计算出了相应的破产时的拉普拉斯变换.本文中的研究方法可以推广到带跳的风险模型,如复合泊松风险模型,这是将来可继续研究的工作.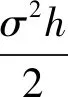
2 方程组的显式解
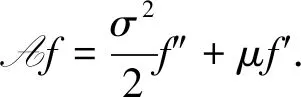
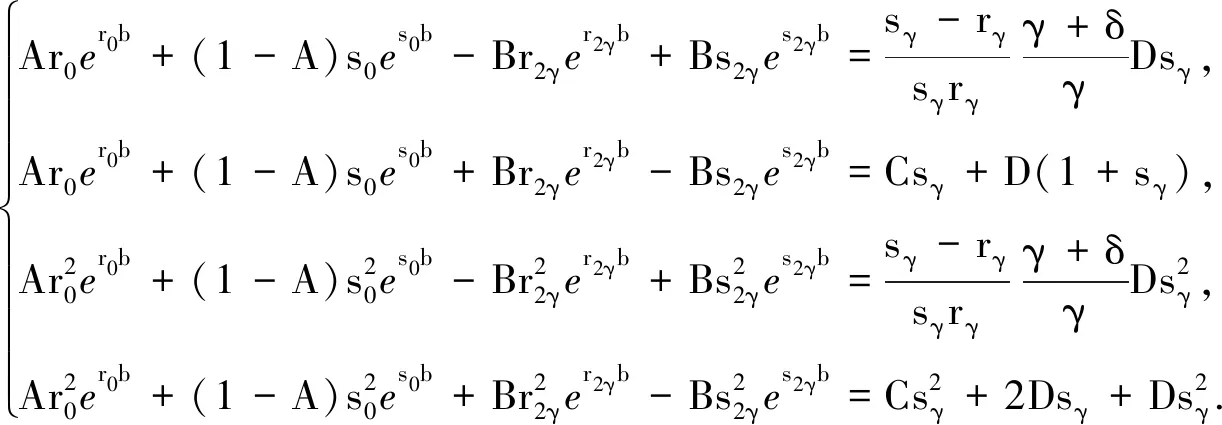

3 结论
