基于熵值分析法的铁路高陡土质边坡安全性评价

伏 坤,刘 勇,王 珣,徐 鑫,李 刚

(中铁二院工程集团有限责任公司,成都 610031)

西南复杂艰险山区铁路建设面临地形高差大、地质环境复杂、高陡地段范围广、边坡稳定性差等难题。如何采用有效的评价方法对边坡开展安全性评估，控制可能存在的风险，为设计、施工及运营提供可靠依据，已经成为路基工程设计中的一个重要课题。

国内外学者针对边坡安全性评价提出了多种边坡安全性评价方法。总体可分为定性评价法、定量评价法及非确定性评价法。定性分析法包括自然(历史)成因法、工程类比分析法、图解法[1-3]等；定量分析法包括极限平衡状态法[4-7]、数值分析法[8-10]等;非确定性方法包括可靠性分析法[11-15]、模糊综合评价法[16-17]、灰色系统评价法[18]等。上述方法已在边坡安全性评价中得到了不同程度的应用，为边坡安全性分析提供了多种新的途径。

以铁路高陡土质边坡为例，利用熵值分析法对土质边坡评价指标进行分析，客观地获得了各评价指标的权重值，避免了人为打分的主观性评价结果。在获得各指标权重结果的基础上，对10例高陡土质边坡开展安全性评价。

1 熵值分析法计算理论

熵值法[19]由信息论之父C.E.Shannon于1948年提出，其为一种客观赋权方法，用作定量描述某个指标的离散程度。熵值越大，表明该指标的离散程度小，该指标对综合评价的权重越小；若熵值越小，表明该指标的离散程度越大，该指标对综合评价的权重越大。采用熵值分析法对铁路高陡土质边坡开展分析的原理和步骤如下。

(1)将土质边坡中定性评价指标按照表1进行量化。

表1 高陡土质边坡定性指标量化

(2)输入高陡土质边坡分析指标，构建分析矩阵。设有n例高陡土质边坡样本，每个样本有m个指标，这n×m个数据构成一个高陡土质边坡特征分析矩阵

(1)

(3)对X分析矩阵进行无量纲标准化处理，评价指标分为效益型(指标越大越优型)和成本型(越小越优型)，计算公式如下。

效益型

(2)

成本型

(3)

(4)根据标准化高陡土质边坡特征分析矩阵X，得到标准化矩阵Y=(yij)n×m

(4)

(5)根据Y=(yij)n×m采用熵值分析法计算评价指标的熵值。表达式为

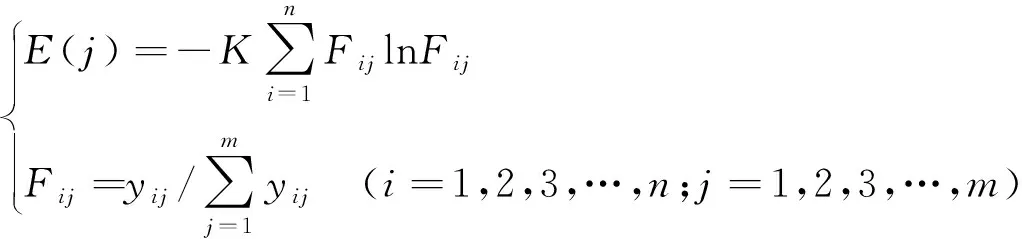
(5)

式中，E(j)表示高陡土质边坡第j个评价指标的熵值；K=1/lnn;Fij为第j个评价指标出现的频率。

(6)计算各评价指标的权重

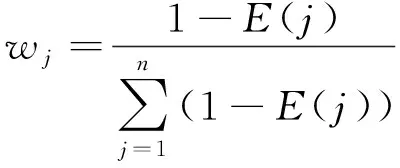
(6)

(7)计算高陡土质边坡的安全性评价结果

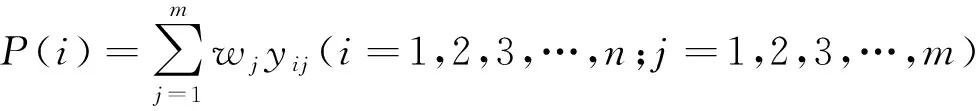
(7)

按照P(i)计算结果给出了高陡土质边坡的安全等级划分标准，见表2。

表2 高陡土质边坡安全等级划分标准

2 基于熵值分析法的应用实例

2.1 工程概况

本文分析数据为文献[20]提供的样本。数据源于贵广线、兰渝线、成渝线等多条西南山区铁路，较为全面反映了西南山区高陡土质边坡呈现的边坡特征、外部环境以及支护措施等。对样本开展深入分析，对于研究山区高陡土质边坡的安全性评价方法及指标具有重要意义。

2.2 铁路高陡土质边坡评价参数的选取

评价指标是边坡安全性评价准确性的基础，但目前尚无统一的评价指标。在参考相关规范要求的基础上，结合目前已有研究成果，选取土质边坡坡度(T1)、边坡坡高(T2)、重度(T3)、含水量(T4)、内聚力(T5)、内摩擦角(T6)、边坡开挖(T7)、边坡支护(T8)、降雨(T9)共计9个指标进行分析。各例高陡土质边坡工点的具体指标见表3。

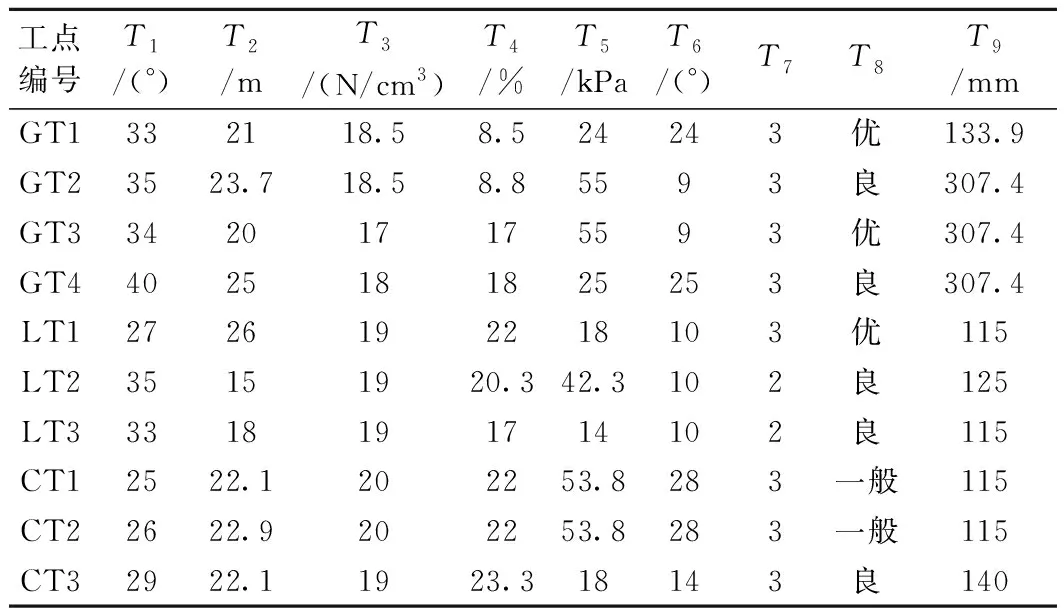
表3 各工点指标值

各指标选取依据如下。

(1)边坡坡度(T1，(°))，指边坡坡面的角度，坡度越大，对边坡安全性影响越大。

(2)边坡坡高(T2，m)，指边坡垂直高度，高度越高，剩余下滑力越大，对边坡安全性影响越大。

(3)重度(T3，N/cm3)，重度越大，对边坡安全性影响越大。

(4)含水量(T4，%)，含水量越大，对边坡安全性影响越大。

(5)内聚力(T5，kPa)，内聚力越大，由内聚力产生的抗滑力越大，边坡越稳定。

(6)内摩擦角(T6，(°))，内摩擦角越大，摩擦系数越大，由此产生的抗滑力越大，边坡越稳定。

(7)边坡开挖(T7，开挖级数)，人类工程活动改变了既有边坡原有应力平衡状态，产生卸荷回弹、应力集中现象，对边坡稳定性影响较大。

(8)边坡支护(T8)，采用支护措施对边坡进行加固，可增加边坡稳定性。

(9)降雨(T9，mm)，降雨易对边坡产生水压力及扬压力，降低边坡稳定性。

2.3 熵值分析法计算与结果分析

以边坡支护情况(T8)为例，阐述熵值分析法的计算过程。在此基础上，对所有指标进行计算，并对计算结果开展分析。

针对边坡支护情况(T8)定性评价结果，首先依据表1对其进行量化，量化结果见表4。

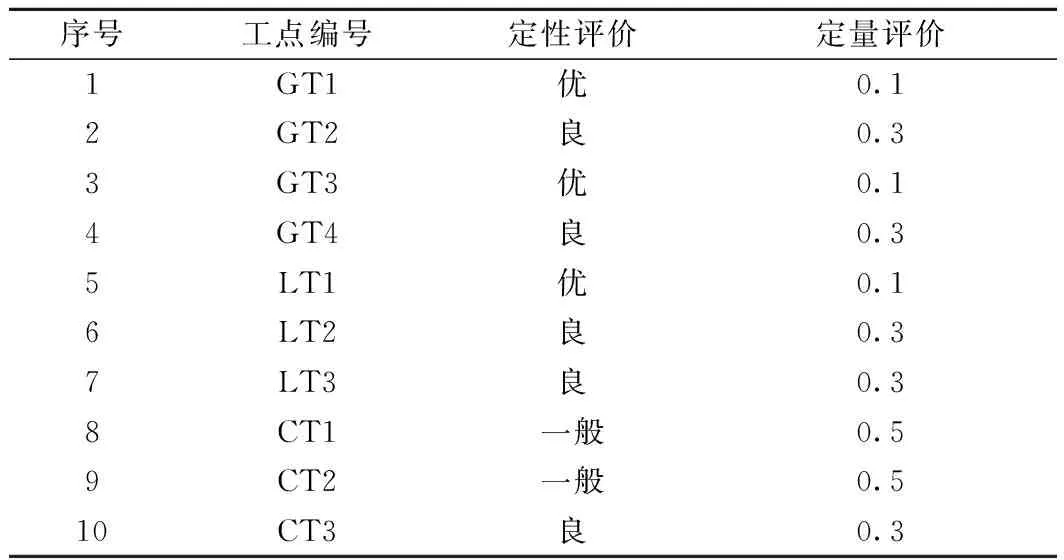
表4 边坡支护情况(T8)量化结果

即由10例高陡土质边坡支护情况(T8)组成的分析矩阵为

X=[0.1 0.3 0.1 0.3 0.1 0.3

0.3 0.5 0.5 0.3]T

边坡支护情况(T8)定性评价指标越好，其量化指标越小，亦即T8为成本型(越小越优型)指标，应采用式(3)对其进行标准化处理，以GT2为例，计算结果为

以此类推，可得到边坡支护情况(T8)标准化矩阵Y=(yij)n×m为

Y=[1 0.5 1 0.5 1 0.5 0.5 0 0 0.5]T

采用式(5)可得到边坡支护情况(T8)的熵值计算结果为0.879 7。

以边坡支护情况(T8)熵值计算过程为基础，可计算得到T1～T9的熵值，依次为0.919，0.882，0.869，0.812，0.848，0.734，0.326，0.800，0.847。熵值越小，表明该指标的离散程度越大，该指标对综合评价的权重越大。从熵值分析结果可知，内摩擦角(T6)和边坡开挖级数(T7)对铁路高陡土质边坡安全性影响较其他指标大。

将熵值计算结果代入式(6)，可得到各指标T1～T9的权重，依次为0.043，0.063，0.070，0.100，0.081，0.141，0.358，0.064，0.081。从熵值法计算得到的权重结果可知，内摩擦角(T6)和边坡开挖级数(T7)对铁路高陡土质边坡安全性影响较其他指标大，与熵值分析结果一致。

将权重结果代入式(7)，可得到10例高陡土质边坡的安全性评价结果，依次为0.101，0.063，0.068，0.063，0.042，0.237，0.230，0.078，0.076，0.044。

依据表2高陡土质边坡安全等级划分标准，可知该10例土质边坡有8处为稳定状态，有2处为基本稳定状态。

将熵值分析法安全性评价结果与专家评价结果进行对比，见表5。

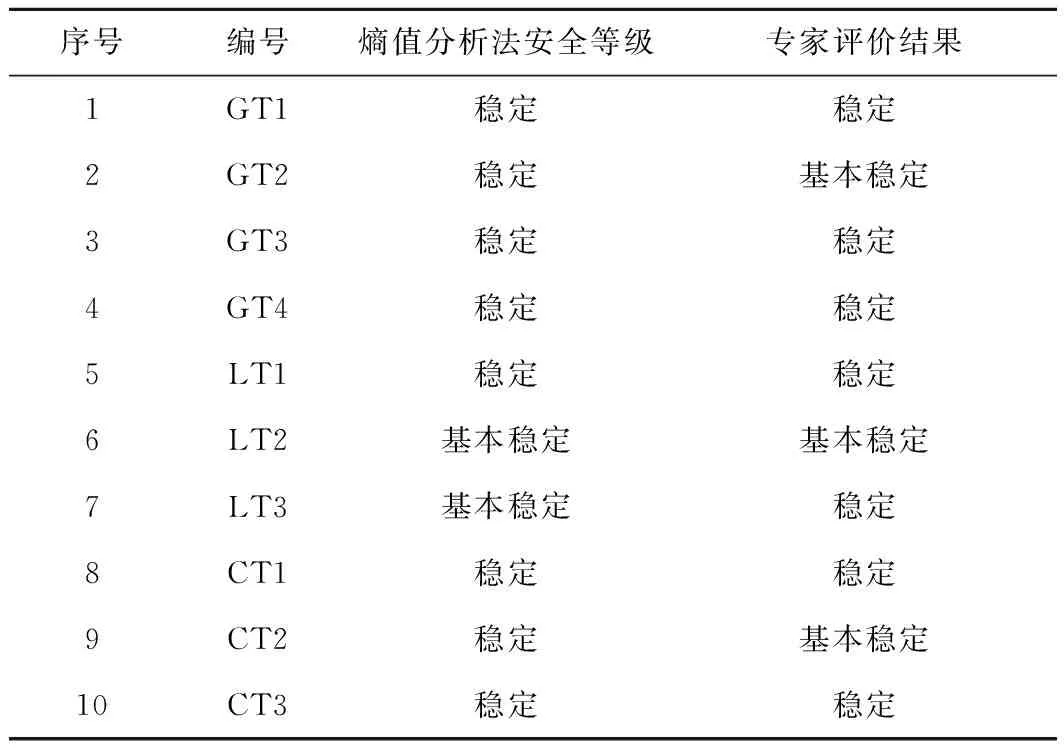
表5 各高陡土质边坡安全等级对比

从表5可以看出，依据熵值分析法，该10例土质边坡有8处为稳定状态，有2处为基本稳定状态。专家评价结果为7处稳定状态，3处基本稳定状态，熵值分析法计算结果与专家评价结果吻合度较高。证明了采用熵值分析法对高陡土质边坡进行安全性评价的合理性，该方法为铁路高陡土质边坡安全性评价提供了新思路。

3 结论

(1)根据10例铁路高陡土质边坡熵值和权重结果可知，内摩擦角(T6)和边坡开挖级数(T7)对铁路高陡土质边坡安全性影响较大。

(2)基于熵值分析法对10例铁路高陡土质边坡安全性开展评价，可知10例土质边坡有8处为稳定状态，有2处为基本稳定状态。

(3)熵值分析法评价结果与专家评价结果吻合度较高，分析结果验证了该方法的准确性及合理性，可为铁路高陡土质边坡安全性评价提供新思路。