考虑直流侧电容存储能量的风电机组虚拟惯性控制策略

杨立滨， 宗 鸣， 李春来

（1. 沈阳工业大学 电气工程学院， 辽宁 沈阳 110870； 2. 国网青海省电力公司清洁能源发展研究院， 青海 西宁810008）

0 引言

大规模风力发电并网运行给电网的安全稳定运行带来了不可忽视的影响，其中频率安全稳定问题是限制风力发电消纳的一个重要因素[1]，[2]。研究表明，当电力系统发生频率扰动时，风电机组的虚拟惯性控制能够在短时间内为系统提供有功支撑，是提升系统频率稳定的一个有效手段。 目前，针对风电机组虚拟惯性控制方面的研究主要集中在两方面：一是在外部配置储能设备辅助风电机组提供惯性支撑[3]，[4]；二是通过风电机组的转子动能 提 供 惯 性 支 撑[5]，[6]。

在外部配置储能设备辅助风电机组提供惯性支撑研究方面，主要通过储能设备与风电机组的协调控制给电网提供惯性支撑。 文献[7]定义了风电-储能系统的虚拟惯量， 研究了储能辅助风电机组惯量调节的容量配置要求，提出了一种基于模糊逻辑的储能-风电场惯量补偿策略。 文献[8]通过研究风电、光伏和储能装置的虚拟惯量控制机理，建立了对应的虚拟惯量动态控制仿真模型。该类方法能够较好地提升风电并网系统的惯性支撑能力，但额外的配置储能设备增加了系统成本。在风电机组的转子动能提供惯性支撑研究方面，通过附加有功控制环建立系统频率和风电机组转子动能之间的关联关系。 文献[9]提出了基于附加转矩控制环的风电机组虚拟惯量控制方法，并通过Bladed 与MATLAB 的联合仿真进行了验证。文献[10]设计了一种风电机组虚拟惯量控制策略的实验平台系统， 对风电机组虚拟惯量控制方法的有效性进行了实验验证。 上述方法只考虑了风电机组转子动能， 未考虑风电机组变流器储能元件的惯量响应能力， 难以有效地充分利用风电机组的惯量响应能力。

本文提出了一种考虑直流侧电容存储能量的风电机组虚拟惯性控制策略。 通过建立风电机组转子动能、 变流器直流侧电容电压和系统频率之间的关联关系， 在系统频率跌落瞬间能够最大化地利用风电机组的惯性支撑能力， 有效地改善了系统的频率调节效果。最后，在PSCAD/EMTDC 仿真软件中建立了风电机组的并网仿真模型， 对所提控制策略进行了验证。

1 风电机组模型及系统频率控制

变速恒频风电机组因其在机组结构、 控制方法等方面的灵活性和优势， 逐渐成为目前的主流风力发电机组。 变速恒频风力发电机组主要由风力机、发电机以及全功率变流器等组成。变速恒频风力发电机的数学模型为[11]

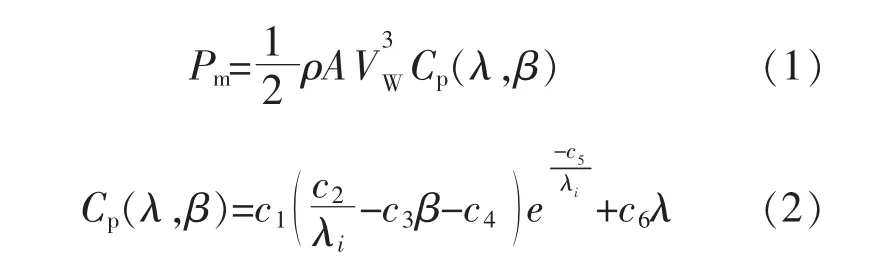
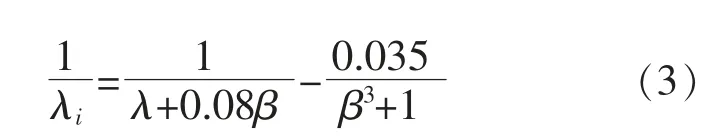
式中：Pm为变速恒频风力发电机组的输出机械功率；ρ 为空气密度；A 为风力机风轮的扫风面积；VW为输入风速；Cp为风能利用系数；β 为风力机的桨距角；λ 为风力发电机组的叶尖速比； 系数c1=0.517，c2=116，c3=0.4，c4=5，c5=21，c6=0.006。

变速恒频风力发电机组的控制系统主要包括风力机转速控制和桨距角控制。其中：风力机组控制系统的参考值主要是有功功率Pref和桨距角β；而背靠背全功率变流器主要分为机侧变流器和网侧变流器，前者控制风力发电机的输出功率，后者控制变流器直流侧电压和风力发电机的无功功率，变流器控制系统均采用PI 控制。 变速恒频风电机组通常包括双馈风电机组和永磁直驱风电机组，两者在惯性控制方面原理类似。本文以3 个双馈风电机组为例， 其有功功率控制基本原理框图如图1 所示。

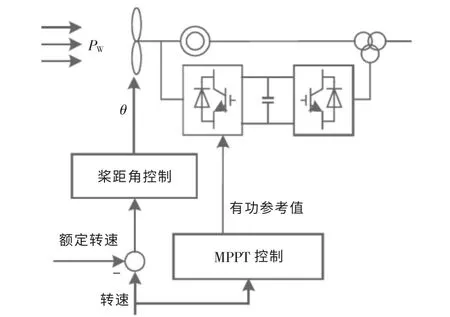
图1 双馈风电机组有功控制基本原理Fig.1 Basic principle of active power control for doubly fed wind turbine

电力系统暂态频率稳定的衡量指标通常包含最大频率偏差、频率最低点时刻、频率变化率以及稳态频率等。 其中最大频率偏差和稳态频率是最为关键的两个指标， 通常作为系统保护装置动作的判断依据。对应电力系统频率响应，通常用下式反映风电接入电力系统的有功-频率之间的不平衡关系：

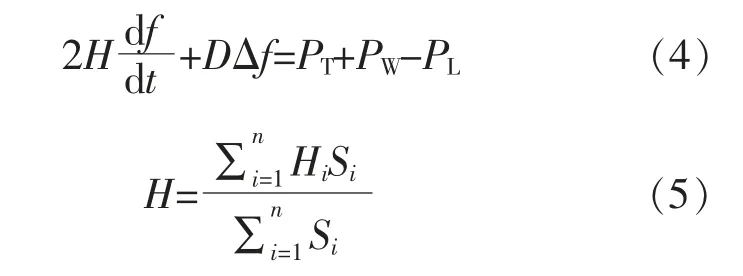
式中：H 为系统的等效惯性时间常数；D 为系统等效的阻尼系数；f 为系统的惯性中心频率；△f 为系统的频率偏差；PT为传统同步机组的输出功率；PW为风力发电机组的输出功率；PL为系统的总负荷大小；Hi，Si分别为同步发电机i 的惯性时间常数、额定容量。

由于风电机组不具备传统同步发电机组的惯性响应能力，当大规模风电机组接入电力系统时， 势必会弱化整个系统的等效惯性时间常数，导致功率缺额瞬间出现较大的频率变化率和频率偏差。 在不平衡功率瞬间，系统的频率偏差较小，系统的频率变化率主要受不平衡功率量以及等效惯性时间所决定。 因此，在系统不平衡功率量一定的情况下，增强系统的等效惯性能够有效降低系统的频率变化率， 提高系统频率控制效果。

2 风电机组虚拟惯性控制策略

本文提出的风电机组虚拟惯量控制策略主要包括转子动能虚拟惯性控制和直流电容虚拟惯性控制， 其基本原理是利用风电机组转子动能和风电变流器直流电容模拟传统同步发电机惯量的协同控制策略。为响应电网频率变化，风电机组功率控制器将调整功率指令值， 使转子转速相应变化来释放转子动能。同时，通过网侧换流器直流电压滑差控制，在电网扰动下，直流电容能相应地吸收或释放能量。

2.1 转子动能虚拟惯性控制

双馈风电机组在实际运行过程中， 转子会存储一定的旋转动能， 双馈风电机组的转速通常为0.7~1.2 pu。为使风电机组具备传统同步发电机的惯性响应能力， 须对风电机组施以和频率相关的附加控制。

当风电机组的初始转子转速为ωr0时， 风电机组所具备的转子动能为

式中：J 为风电机组的转动惯量。

当风电机组转子转速从初始的ωr0变化到ωr1时，风电机组转子吸收或者释放的动能为

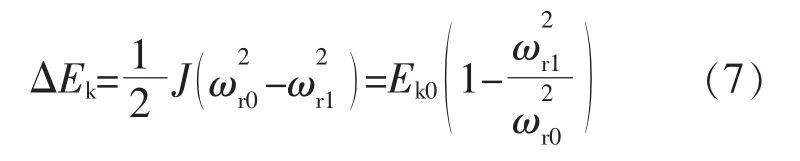
风电机组在转速变化瞬间所吸收或者释放的有功功率为

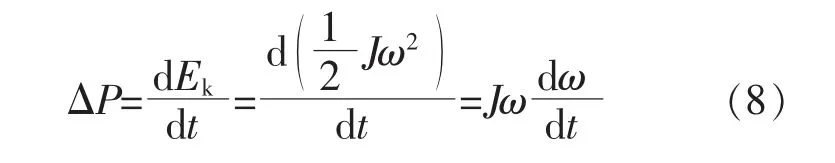
式中：ω 为风机的实时转速。

由此可以看出， 风电机组可通过改变控制方式来释放转子所存储的动能， 以响应系统的频率变化。

基于转子动能的虚拟惯性控制是在风电机组最大功率跟踪基础上， 引入频率偏差成正比例以及频率微分成正比例的附加有功， 使得风电机组在系统频率发生变化时能够释放一定的转子动能，从而模拟传统同步发电机组的惯性响应能力。基于转子动能的虚拟惯性控制原理框图如图2 所示。

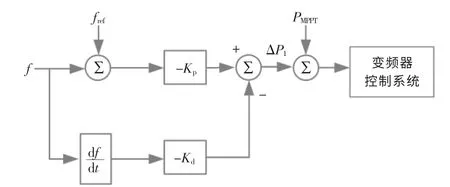
图2 基于转子动能的虚拟惯性控制策略Fig.2 Virtual inertial control strategy based on rotor kinetic energy

风电机组转子动能参与频率调节的有功变化量可表示为

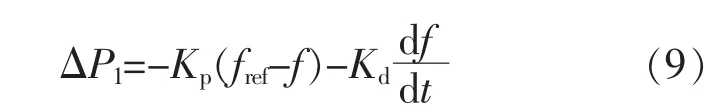
式中：Kp和Kd分别为比例系数和微分系数；fref为频率参考值；f 为频率实际值。

2.2 直流电容虚拟惯性控制

除了风电机组的转子动能外， 风电机组变流器直流侧电容的能量也能补偿系统频率变化瞬间的功率不平衡量，以响应系统的频率变化。变流器直流侧电容主要用于功率平衡， 任何情况下直流侧电压的变化都表明变流器机侧以及网侧有功功率的不平衡。 风电机组变流器直流侧电容的动态特性为

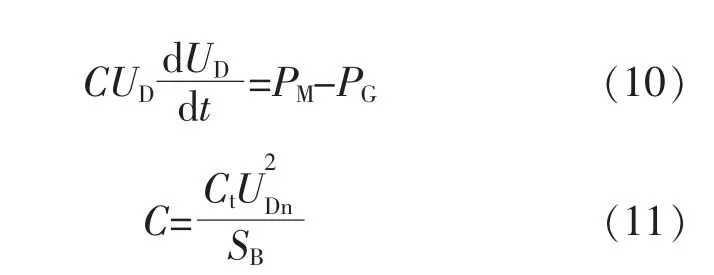
式中：UD为变流器直流侧电压的标幺值；UDn为变流器直流侧电压的额定值；SB为系统的基准容量；C 为变流器直流侧电容；Ct为变流器直流侧电容等效值；PM为风电机组机侧变流器输出的有功功率；PG为风电机组网侧变流器输出的有功功率。

为简化分析，忽略变流器自身的有功损耗。为利用变流器直流侧电容的能量模拟同步发电机的惯性响应能力，PM类似于同步发电机的机械功率。 假设PM为一恒定量，这是因为风电机组的惯性支撑不仅来源于直流电容， 还和上述分析的转子动能有关。 另外，PG可近似认为是风电机组的电磁功率， 则变流器直流侧电压的变化从某种意义上来讲类似于发电机的转速量。 与传统同步发电机相比, 最根本的差别在于风电机组变流器直流侧电压提供的是虚拟的惯量， 而同步发电机的转速与系统频率相关。结合式（4）和式（11），可得：

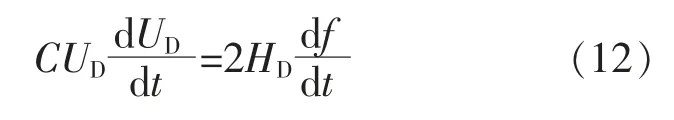
式中：HD为风电机组变流器直流侧电容提供的等效惯性时间常数。

对式（12）两边分别进行积分可得：

式中：UD0为变流器直流电压的平衡点；f0为系统频率的平衡点。

风电机组变流器直流侧电容的能量虽然能够为系统提供一定的频率支撑， 但是风电机组实际运行时不允许直流电压波动范围较大。 本文结合实际工程经验和变流器运行工况， 将变流器直流侧电压波动限制在±10%以内。由于变流器直流侧电压的波动范围不大， 因此可在UD0处进行一阶泰勒级数展开，如下所示：

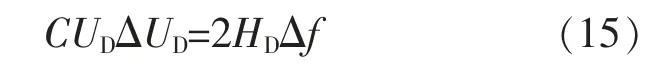
根据式（15），得到基于变流器直流侧电容的虚拟惯性控制策略为

式中：KD为虚拟惯性控制参数。进一步可得：

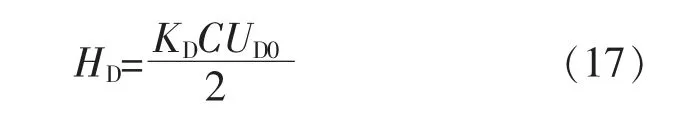
由式（17）可以看出，直流电容虚拟惯性控制策略的虚拟惯量主要和虚拟惯性控制参数、 直流侧电容以及直流侧电压相关， 也即说明直流电容虚拟惯性控制效果和此类参数相关。

根据上述分析， 直流电容虚拟惯性控制策略的基本原理框图如图3 所示。

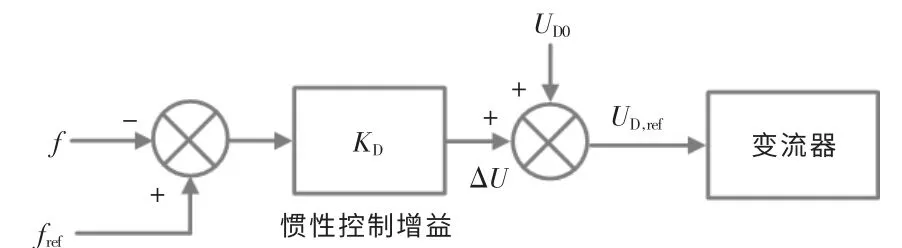
图3 基于直流侧电容的虚拟惯性控制策略Fig.3 Virtual inertial control strategy based on DC side capacitance

本文所提的考虑直流侧电容存储能量的风电机组虚拟惯性控制同时利用风电机组的转子动能和变流器直流侧电容的能量， 补偿系统频率变化时的不平衡有功量。 相较于单一的转子动能虚拟惯性控制策略而言， 在保证风电机组安全稳定运行的同时能够提供更多的能量来影响系统频率的变化，从而达到更好的频率支撑效果。

3 算例分析

为验证本文所提风电机组虚拟惯性控制策略的有效性， 在PSCAD/EMTDC 软件中建立如图4所示的仿真测试系统， 将考虑直流侧电容存储能量的风电机组虚拟惯性控制策略（记为所提控制策略）与风电机组不采取惯性控制、传统仅采用转子动能的惯性控制策略（记为传统控制策略）的效果进行了对比。 同步发电机基本参数如下：容量为100 MV·A，机端电压为13.8 kV，惯性时间常数为5 s。风电机组基本参数如下：容量为6 MV·A，机端电压为0.69 kV，风力机惯性时间常数为4 s，变流器直流电容为7 500 μF。 变压器参数如下：风电机组变压器变比为0.69 kV∶10 kV， 发电机变压器变比为13.8 kV∶10 kV。 系统负荷容量为50 MW。

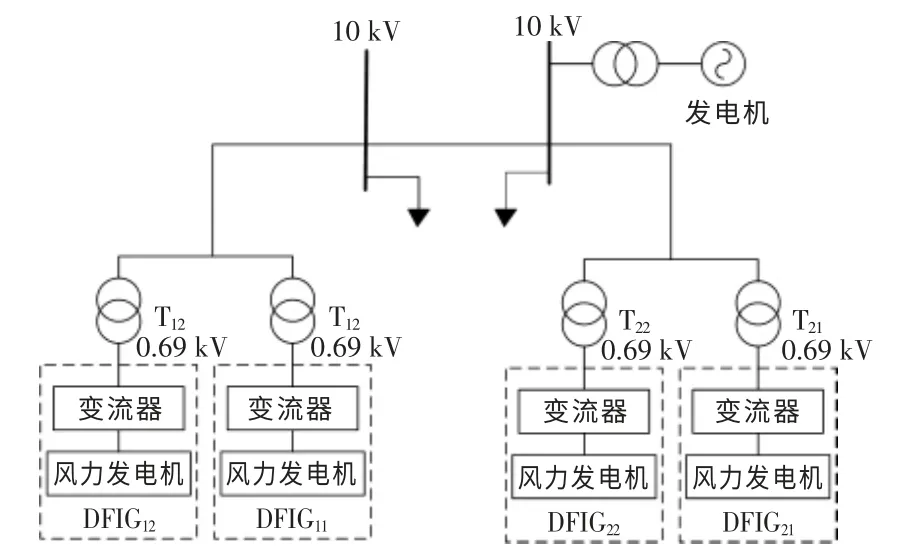
图4 仿真系统Fig.4 Simulation system

仿真中在第10 秒投入一定的有功负荷，系统由于有功缺额而发生频率下降。

图5 为3 种控制策略下系统频率响应的对比结果。 可以看出，相较于传统控制策略，采用所提控制策略后系统频率下降的速率明显下降。 这是因为所提控制策略在释放风电机组转子动能的同时，能够从直流电容侧释放一定的能量，因而响应频率变化时所释放的能量更多。结果表明，所提控制策略能够给系统提供更强的惯性支撑作用，且系统的频率最低点也得到了改善， 更有利于系统的稳定性。

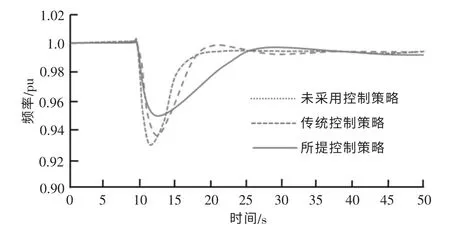
图5 系统频率Fig.5 System frequency

图6 为传统同步发电机的有功功率响应曲线。可以看出，由于所提控制策略下的风电机组释放的能量更多，当系统发生功率缺额时，传统同步发电机的有功功率下降幅度最小。

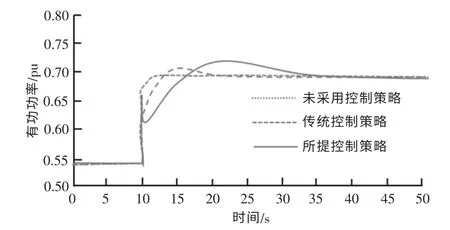
图6 同步发电机有功功率Fig.6 Active power of synchronous generator

图7 为风电机组的有功功率响应曲线。 可以看出， 所提控制策略在系统频率跌落瞬间能够释放更多的有功功率， 且经过一段时间的调整之后逐渐恢复至初始值。 这是因为风电机组电容能释放一定的能量且该能量是瞬时的。 图8 为风电机组变流器直流侧电压的变化情况。可以看出：所提控制策略在系统频率变化瞬间， 风电机组变流器的直流侧电压也会发生改变， 以响应系统的频率变化；而传统控制策略下的直流侧电压保持不变，且直流电压在允许的变化范围之内。

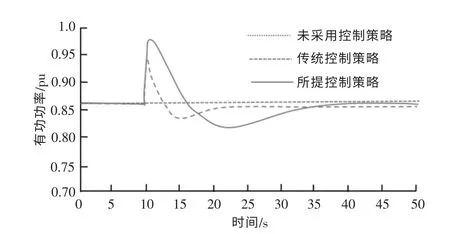
图7 风电机组有功功率Fig.7 Active power of wind turbine

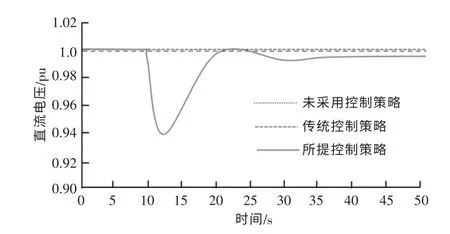
图8 风电机组变流器直流侧电压Fig.8 DC side voltage of wind turbine converter

从上述仿真结果可以看出， 相较于传统控制策略， 本文所提控制策略在保证风电机组变流器直流电压安全稳定运行的情况下， 能够更多地利用风电机组的惯性支撑能力，频率调节效果更好。

4 结论

本文提出了一种考虑直流侧电容存储能量的风电机组虚拟惯性控制策略， 建立了系统频率和风电机组转子动能、 变流器直流电压之间的函数关系。 该策略同时利用风电机组的转子动能和变流器直流侧电容来提升电力系统的整体惯性水平，相比传统的惯性控制策略，在保证风电机组变流器直流电压安全稳定运行的情况下， 能够更多地利用风电机组的动能来提升惯性支撑能力，达到更好的频率调节效果。