计及复杂气象影响的含光伏电源的母线峰值负荷预测

朱赫炎， 于长永， 贺庆奎， 宋 坤， 刘靖波， 许言路， 卢天琪， 黄南天

（1.国网辽宁省电力有限公司 经济技术研究院， 辽宁 沈阳 110015； 2.东北电力大学 电气工程学院， 吉林吉林 132012）

0 引言

母线峰值负荷预测是保障电力系统可靠稳定运行的重要依据，也是评估系统清洁能源（光伏、风电等可再生能源）消纳能力的重要保障。 光伏DG 受温度、风速、湿度、不同气象日的影响，其出力波动剧烈，在接入配电网后，会加剧母线峰值负荷的波动。 为了实现高精度母线峰值负荷预测，有效提高配电系统清洁能源（特别是光伏电源）的消纳能力，在高渗透率光伏电源接入场景下， 必须考虑DG 接入电网对母线峰荷预测的影响。

在母线负荷预测建模过程中，需要考虑多种因素对母线负荷的影响。 文献[1]研究了环境因素对母线负荷的影响，通过快速属性约简法研究影响因素与母线负荷间关系，找出对母线负荷影响大的因素，提高母线负荷预测精度。 文献[2]建立了特征向量矩阵， 找出并调整数据中的异常数据，分析相关因素与负荷间的相关性，构建负荷水平相似集，根据待测负荷日与相似集选择相似日，实现对母线负荷的综合预测。 文献[3]分析了母线源荷负荷属性，然后将不同属性负荷进行分类，分别研究有源网络中的电源和负荷成分，优化了母线负荷预测。上述文献优化了母线负荷预测，但是没有充分分析自然气象、 社会等因素对母线负荷的影响，没有进行特征选择。

现有涉及峰荷预测的研究中， 多针对城市级电网峰值负荷的影响因素和预测方法开展。 传统负荷预测方法有灰色模型和回归分析等， 当负荷发生非线性波动时， 传统负荷预测方法预测精度受限[4]～[5]。 文献[6]分析了城市负荷波动的内因，考虑了多源数据对负荷波动的影响， 通过皮尔逊相关系数和互信息计算多源数据和负荷波动的相关性，选择与负荷波动强相关的自然特征、社会特征和其它特征， 并应用支持向量回归模型预测峰值负荷。 文献[7]提出了基于人工神经网络演变的峰值负荷预测模型， 通过最优特征集合预测峰值负荷，且根据不同实验间的对比，验证了所提方法具有预测精度高的优点。 文献[8]针对负荷预测方法的缺点， 优化了基于模糊支持向量机的核回归方法。现有研究在一定程度上提高了峰荷预测精度，但尚未针对母线峰值负荷预测中， 历史数据有限和接入光伏DG 后， 母线峰荷波动特性复杂化的问题开展分析。 极限学习机 （Extreme Learning Machine，ELM）所需训练样本少，能够解决具有非线性波动特点的母线峰值负荷预测的难题，且预测精度高[9]，[10]。

为分析复杂气象数据和光伏DG 接入后对母线峰值负荷的影响，并解决母线峰值负荷历史数据有限、预测精度低的不足，本文提出了计及复杂气象影响的母线峰值负荷预测方法。根据不同气象日母线峰值负荷的波动情况， 在晴天、阴雨和多云3 种天气情况下，分别通过条件互信息（Conditional Mutual Information， CMI）分析高维气象、 社会等特征与母线峰值负荷间的相关性，获得特征重要度排序。本文采用适合小样本训练的改进粒子群优化极限学习机（Improved Particle Swarm Optimization -Extreme Learning Machine，IPSO-ELM） 作为预测器， 并以IPSOELM 预测精度为决策变量， 确定在不同气象日下的最优特征子集；根据最优特征子集，分别建立了在不同气象日下母线峰值负荷最优预测模型。

1 母线峰值负荷的波动性展示

某城市含高渗透率光伏电源的母线峰值负荷和日负荷实际值如图1 所示。

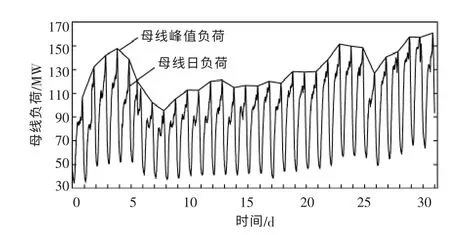
图1 含光伏DG 母线日负荷和峰值负荷Fig.1 Daily load and peak load for electric bus with PV DG

由图1 可知，母线峰值负荷的最大值和最小值分别为160.7 MW，102.2 MW。 与电力负荷相比，母线波动性更大。 母线峰值负荷每天仅累积一组数据，历史负荷数据有限，预测模型训练难度大。而且母线负荷由于有DG 的存在， 母线峰值负荷在不同气象日下波动情况也会不同，预测困难。

2 基于条件互信息的特征选择方法

2.1 母线峰值负荷预测原始特征集合构建

高维气象（经度、纬度、温度、气压、湿度、风速等）、社会（日期、节假日等）等多种因素都会导致母线峰值负荷发生波动， 同时考虑光伏DG 对母线负荷的影响，通过分析和研究相关文献，构建的原始特征集合如表1 所示。

表1 母线峰值负荷预测原始特征集合Table 1 Original feature set of peak load prediction for electrical bus

2.2 条件互信息

由表1 可知， 含光伏DG 的母线峰值负荷影响因素众多，如果考虑全部影响因素，将会造成信息冗余，母线峰值负荷预测精度低。为提高母线峰值负荷预测精度，通过CMI 分析各影响因素与母线峰值负荷间的相关性，并通过特征选择，避免母线峰值负荷预测时出现特征冗余，提高预测精度。

在母线峰值负荷预测中，设D 为包含自然气象、社会等多种因素的原始特征集合；d 为D 中某一特征；Q 为实测母线峰值负荷集合；q 为集合Q中某一母线峰值负荷集合；Z 为已选择的特征集合。 D 和Q 间的互信息为

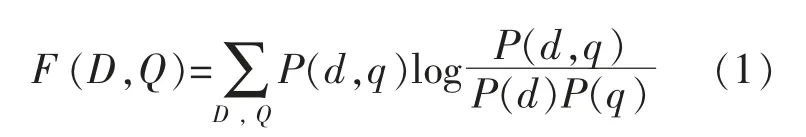
式中：P（d），P（q）分别为D，Q 的边际密度函数，其中，P（d）为D 中取d 的概率，P（q）为Q 中取q的概率，P（d，q）为D 和Q 的联合概率密度；P（d，q）为D 中取d，Q 中取q 的联合概率。

在已知Z 集合的条件下，集合D 与实测母线峰值负荷值Q 的条件互信息为

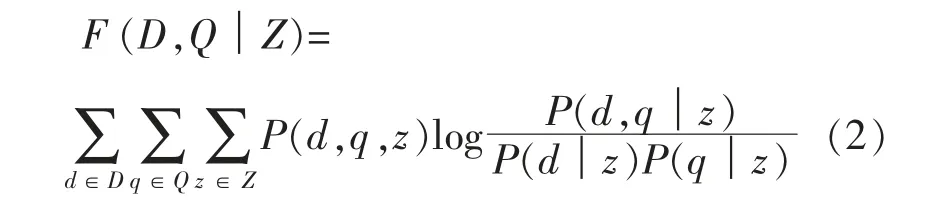
式中：P（d│z），P（q│z）分别为在Z 条件下D，Q的概率密度函数；P（d，q│z）为在Z 条件下D，Q的联合概率密度函数；P （d，q，z） 为D，Q，Z 的联合概率密度函数。

与传统互信息方法相比，CMI 在分析过程中，考虑了特征集合内特征间冗余性， 更加适合降低最优特征子集中信息冗余。

3 基于改进粒子群优化的极限学习机原理

以有限的母线峰值负荷数据训练神经网络等预测器，难以获得理想的预测模型。 因此，应用适用于小样本训练的ELM 构建母线峰值负荷预测器。为避免参数选择不当，应用改进粒子群算法优化ELM 的初始值和阈值，进一步提高预测精度。

3.1 极限学习机

设有N 个样本{（xi，ti）}Ni=1，其中，输入数据为xi=[xi1，xi2，…，xin]T∈Rn，目标输出值为ti=[ti1，ti2，…，tim]T∈Rm。 则单隐层神经网络（隐层节点的数目为L）的ELM 网络模型为

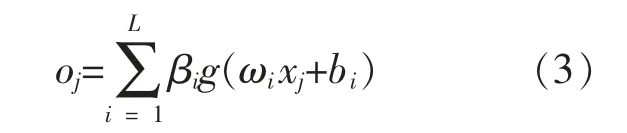
式中：oj为网络输出值；g（x）为激活函数；ωi为输入权重；βi为输出权重；bi为第i 个隐层单元的偏置。

无误差时， 激活函数无限接近任意N 个样本，则N 个方程矩阵为

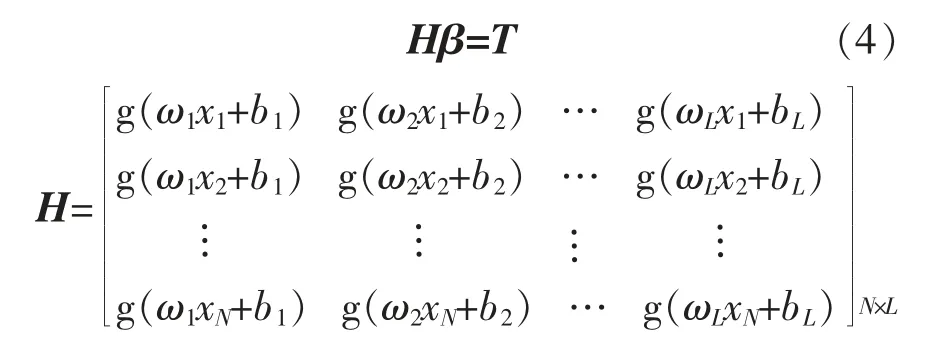
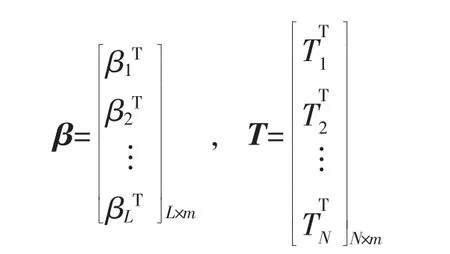
其中：H 为隐含层节点输出；T 为期望输出。

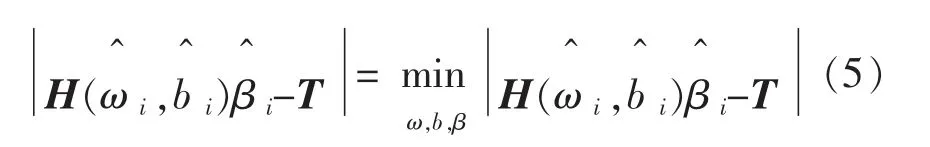
与式（5）等价的最小损失函数为

在ELM 算法中，ω 和b 被随机确定后， 即可获得唯一H，便可确定ELM 结构。

3.2 基于改进粒子群的极限学习机参数优化

3.2.1 改进粒子群原理

传统粒子群算法存在寻优时间长、 容易出现局部最优的问题[11]。本文采用改进粒子群算法，通过改变惯性权重， 解决传统粒子群算法全局最优解易发生波动的问题。 惯性权重表达式为

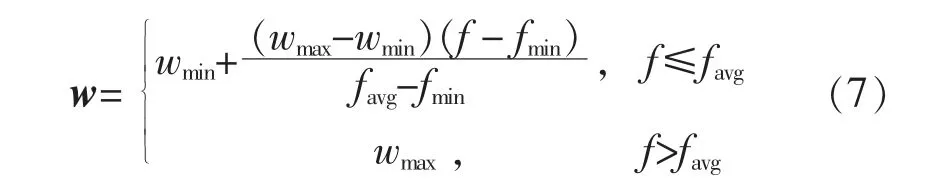
式中：wmin，wmax分别为惯性权重最小值、最大值；f为粒子适应度；favg为平均适应度；fmin为最小适应度。

为了快速确定全局最优解， 对算法进行动态调整，即：

式中：c1s和c2s分别为c1和c2的初值；c1c和c2c分别为c1和c2的终值；iter 为当前迭代的次数；itermax为总迭代的次数。

3.2.2 基于改进粒子群的ELM 参数优化

以原始特征集合构建含光伏母线峰值负荷预测模型最优过程为例， 展示IPSO 优化ELM 过程如下：

①基于原始特征集合构建含光伏母线峰值负荷预测ELM（特征集合如表1 所示），并随机产生ELM 的输入权值ω 和阈值b；

②确定输入含光伏母线负荷峰值预测所需原始特征集合信息的样本X， 且以理想精度或迭代次数为结束条件；

③针对样本数据，开展归一化处理；

④根据ELM 的含光伏母线峰荷预测的MAPE 获得适应度值， 并确定当前个体和群体最佳适应值；

⑤在传统PSO 基础上，根据式（7），（8）更新粒子速度与位置；

⑥计算当前粒子适应度值。 然后与历史最优值比较，如更优，则更新粒子最优解；否则维持个体最佳适应度值；

⑦如果当前粒子的适应度值比群体最优解更优，则更新群体最优解；否则，维持群体最优解不变；

⑧如未达到结束条件，则返回③；否则，将最优解ω 和b 代入ELM，构建最优含光伏母线负荷峰值预测模型。

本文对不同维度特征集合构建针对性最优ELM 预测器，均采用以上方法。

4 实验及分析

本文应用某地区2018 年母线峰值负荷和气象信息数据，在不同气象日下，对含光伏DG 母线分别开展针对性特征选择。 为证明新方法的先进性， 以IPSO-ELM 与ELM 和BP 神经网络（Back Propagation Neural Model，BPNN）作对比实验。 以平均绝对百分比误差 （Mean Absolute Percent Error，MAPE）、 均 方 根 误 差 （Root Mean Square Error，RMSE）评估模型预测效果，指标计算方法为

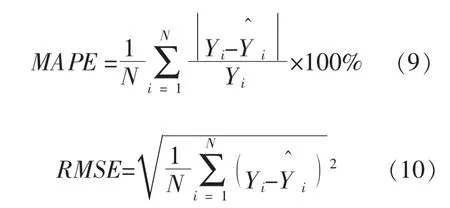
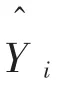
4.1 基于CMI 的特征选择分析

在含光伏DG 的母线峰值负荷预测中，首先，在晴天、 阴雨和多云3 种情况下， 分别通过CMI分析高维气象、 社会等特征与母线峰值负荷间的相关性， 获得特征重要度排序； 然后， 以IPSOELM 为预测器，把预测结果的MAPE 值作为决策变量，根据特征重要度排序结果，进行前向特征选择， 得到不同气象日下母线峰值负荷预测的最优特征子集，降低原始特征集合内特征间的冗余性，提高含光伏DG 母线峰值负荷预测的精度。

为了展示在不同气象日下、 不同特征对含光伏DG 母线峰值负荷的特征重要度不同， 通过CMI 计算各特征对母线峰值负荷的特征重要度。图2 给出了某地区含光伏DG 的某条母线， 在晴天、多云和阴雨3 种气象日下的特征重要度。

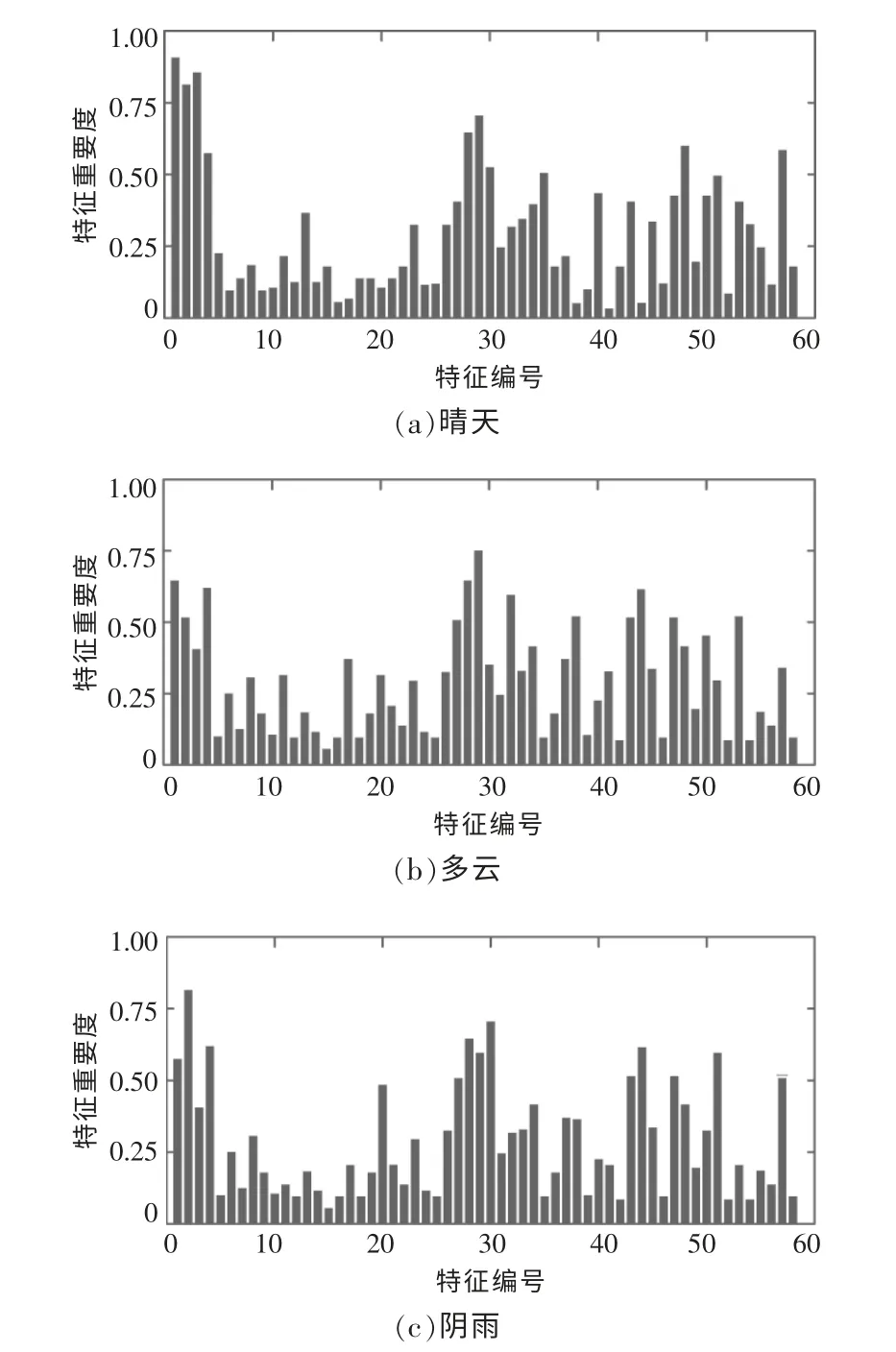
图2 不同气象日特征重要度分析Fig.2 Significance analysis of different meteorological daily features

由图2 可知，不同气象日场景下，不同因素对母线峰值负荷的特征重要度不同。 例如在10~20号特征中，晴天时，F10和F12特征重要度高；在多云时F10、F17和F20特征重要度高；阴雨时，F20特征重要度高。3 种气象日最优特征集合选择如图3 所示。

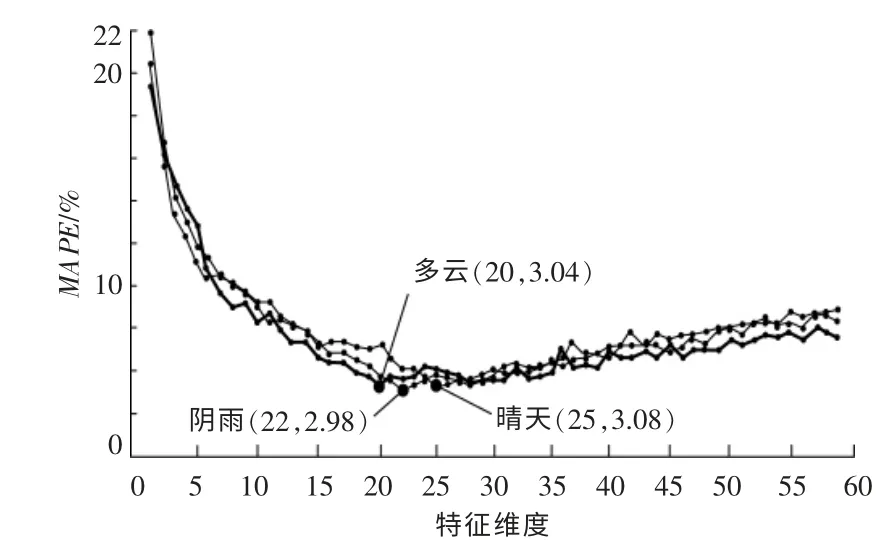
图3 最优特征集合选择过程Fig.3 Optimal feature set selection

由图3 可以看出，随着特征维度的增加，母线峰值负荷预测的误差越来越小， 当特征维度增加到一定数量时，母线峰荷的预测误差达到最小值。此时，输入特征的集合为最优特征集合，阴天、晴天和多云3 种气象日下的最优特征集合维数分别为22，25 和20， 且对应预测的MAPE 值分别为2.98%，3.08%和3.04%。 因此，在含光伏DG 的母线峰值负荷预测中，为了避免出现特征冗余，需要进行特征选择，提高预测精度。

表2 对应图3 中3 种气象日下， 最优特征集合选择结果。

表2 最优特征集合Table 2 Optimal feature set

由表2 可知， 不同气象日最优特征集合包含的特征个数不同，晴天时特征个数最多，多云时特征个数最少。且同一特征在不同气象日，对母线峰值负荷的特征重要度排序不同，F1 的特征重要度在晴天时排在第一， 在多云时排在第三，在阴雨天时排在第九。 对于含光伏DG 母线峰值负荷预测，在3 种不同气象日下，最优特征集合存在差异，因此，需要针对不同气象日，分别进行特征选择，确定不同的最优特征集合，针对性建立不同气象日下，最优预测模型。

4.2 含光伏DG 的母线峰值负荷预测结果分析

本文列出2018 年7 月第1 周， 某条含光伏DG 的母线峰值负荷预测结果。 图4 为母线针对性建模和采用原始特征集合建模的预测结果。

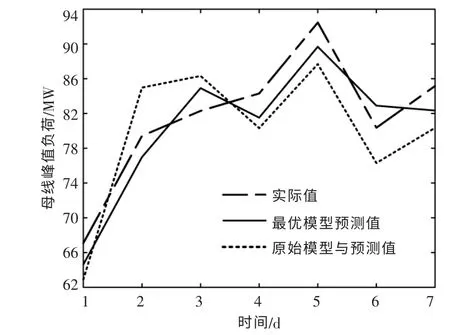
图4 最优模型和原始预测模型峰值负荷预测Fig.4 Optimal model and original prediction model for peak load prediction

表3 为对应图4 中母线峰值负荷预测曲线的误差结果。

表3 母线峰值负荷预测误差Table 3 Error of peak load prediction for electric bus

在最优模型下， 母线峰值负荷预测的MAPE值为3.021%；利用原始特征集合建模时，母线峰值负荷预测的MAPE 值为4.352%。 对比可知，根据不同气象日开展的特征选择， 并建立不同母线峰值负荷预测模型， 可有效提高不同气象日下含DG 的母线峰值负荷预测精度。

不同算法，在第2 周的母线峰值负荷预测结果如图5 所示。

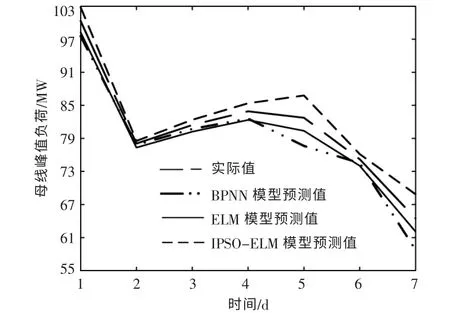
图5 3 种方法的峰值负荷预测Fig.5 Three methods of peak load prediction

表4 对应图5 中3 种预测方法下的预测曲线误差结果。

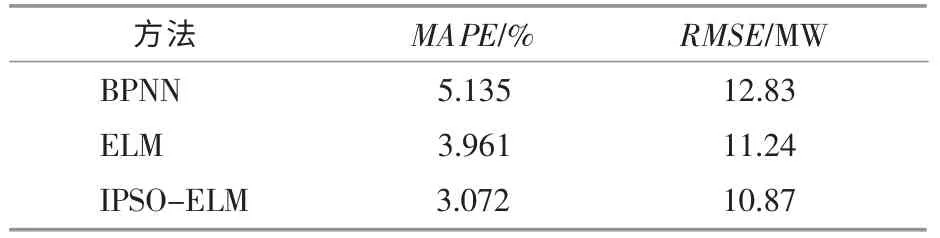
表4 3 种方法的母线峰值负荷预测误差Table 4 The peak load prediction errors of the three methods

由表4 中可以看出，分别应用BPNN，ELM 和IPSO-ELM 预测母线峰值负荷时，MAPE 值分别为5.135%，3.961%和3.072%，IPSO-ELM 对含DG 母线负荷预测的MAPE 值最小。 因此，本文应用DG 的IPSO-ELM 预测器， 对于含光伏DG 的母线峰值负荷进行预测，预测精度高。

5 结论

本文提出计及复杂气象影响的母线峰值负荷预测方法，该方法具有以下优点：①以CMI 值为依据，开展母线峰值负荷预测特征选择，降低了母线峰值负荷预测时，特征冗余对预测精度的影响；②针对晴天、 多云和阴雨3 种气象日分别构建最优预测模型， 含光伏DG 母线峰值的预测精度显著提高；③对于母线峰值负荷历史数据少的问题，提出应用IPSO-ELM 作为预测器，满足小样本场景下预测精度需要。