海外工程UTM坐标投影变形的特点及消除方法
2020-06-18孙洪瑞吴卫平
孙洪瑞,吴卫平
(中交第三航务工程勘察设计院有限公司,上海 201612)
随着中国综合国力和工程技术水平的不断提高,以及一带一路倡议规划的需要,海外工程测量越来越多,尤其是在亚非拉等欠发达地区。有些国家甚至没有大中比例尺地形图和国家控制网,给坐标系的建立和选择带来一定的难度。目前世界上有一百多个国家与地区在使用通用横墨卡托(universal transverse Mercator,UTM)投影的坐标,如刚果(布)的国家坐标系统为CONGO60,参考椭球为克拉克1880 IGN,为UTM投影坐标;加蓬国家坐标系采用UTM投影坐标,参考椭球为GRS80;东南亚的孟加拉国、缅甸、菲律宾等国家坐标系也是采用UTM投影坐标。了解UTM坐标的特点,采取有效方法消除投影后的长度变形,确保测量成果满足设计与施工规范的要求,即投影长度变形值小于2.5 cmkm[1],变形因子小于140 000,这对今后海外工程建设具有非常重要的参考意义。
1 UTM坐标的定义
UTM坐标是指采用通用横轴墨卡托投影方式得到的坐标。UTM投影的坐标,角度没有变形,中央子午线为直线,且为投影的对称轴,按经度分为60个带,每带6°,从180°W起算,两条标准子午线距离中央子午线180 km左右[2]。UTM坐标系统是美国编制世界各地军用地图和地球资源卫星图像所采用的坐标系统,是世界上常用的地图投影方式,有别于我国的高斯投影坐标系统。
2 UTM投影与高斯投影的区别
UTM投影与高斯投影都是横轴墨卡托投影演变而成的投影方式,但两者之间却有明显的区别,其主要区别包括4点:
1)投影法则不同。UTM投影采用等角横轴割圆柱投影,而高斯投影采用等角横切圆柱投影。
2)中央子午线长度比不同。UTM投影中央子午线的投影长度比为0.999 6,中央子午线长度直接缩小0.000 4;而高斯投影中央子午线投影长度比为1,投影后尺寸未变。UTM投影变形比例因子为1的地方是在割线上(距离中央经线约±1°40′),即距离中央子午线约±180 km。
UTM投影坐标与高斯投影坐标可采用近似的换算关系:xUTM=0.999 6x高斯,yUTM=0.999 6y高斯,换算误差约为1 m左右[3]。
3)分带编号(Zone)不同。UTM投影带号是从180°W开始起记,间隔6°为一带,由西向东计数,故第1带的中央经度L0=-177°W;高斯投影自零子午线起每隔6°为一带,第1带的中央经度L0=3°。
4)平面坐标加常数不同。高斯投影的平面坐标x不变,y坐标统一加上500 km,即x实=x,y实=y+500;而UTM投影的平面坐标对于南北半球区别对待,换算关系如下:
(1)
3 UTM投影变形分析
3.1 变形原理
地图投影是将椭球面各元素(包括坐标、方向和长度)按一定的数字法则投影到平面上。这一数学法则的方程式表示为[4]:
(2)
式中:(L,B)为椭球面上某点的大地坐标,其中L、B分别为经度、纬度;(x,y)为该点投影后的平面直角坐标。
等角投影满足的特征方程为:
(3)
式中:r为参考椭球面卯酉圈曲率半径;M为参考椭球面子午圈曲率半径。
由于UTM投影的中央子午线投影长度比m0=0.999 6,UTM投影长度比m、长度变形量V的实用简化计算公式如下[5]:
(4)
式中:ym为测量边横坐标的平均值;Rm为参考椭球面的平均曲率半径。
3.2 变形定量分析
长度投影变形值由以下两部分组成:
1)地面实际边长AB归算到参考椭球面边长的改正(高程归化改正),见图1,其改正值为:
(5)
式中:Hm为测量边的平均高程值;H0为投影面的高程值;R为地球半径。
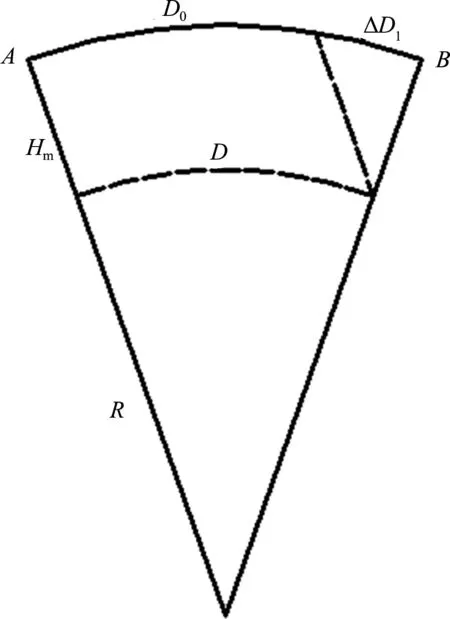
图1 高程归化改正原理
2)参考椭球面投影至平面的改正(投影改正),其改正值为:
(6)
(7)

综上,测量边长按照UTM投影后的长度总变形量为:
(8)
3.3 消除投影变形的基本原则
为消除或降低投影变形,通常通过建立合适的坐标系来解决,其基本原则为:
1)在满足测绘行业规范要求的基础上,为使测量结果一测多用,应采用国家统一的平面坐标系,即建设工程的测量控制网应同国家测量系统一致。
2)当长度的归算改正不能满足上述要求时,为确保测量结果可以直接利用或方便计算,可采用任意带的独立平面坐标系。
3.4 解决变形的两种方法
1)工程测量规范中给的消除投影变形的基本方法,即通过选择合适的高程参考面和中央子午线来建立独立坐标系,具体做法为:
①通过调整Hm从而选择合适的高程参考面,抵偿分带投影变形,但是一般高程参考面不得高于测区平均高程。
施工流程为:土方开挖、回填→土工布铺设→土工笼袋铺设→土工笼袋装填→土工笼袋封盖。铅丝石笼在施工区域外成型后运至铺设区域内。人工将岸坡铅丝石笼从护脚处开始至坡顶依次错缝向上码放,并用铅丝将笼体与相邻笼体进行固定。成品土工石笼袋放入铅丝石笼内时将袋口处先拉高10cm,将底部四方平均撑开,袋口用绑丝与铅丝石笼简单连接加固,防止填料时袋子变形。采用长臂挖掘机进行土料袋填,完成后人工将机械未填满的袋子进行补填,土工石笼袋封口前,填充较小石料使袋顶高出8cm再封口。
②调整ym,即平移中央子午线,以抵偿由高程面的边长归算至参考椭球面上的投影变形。
③不仅调整Hm(改变高程参考面),而且调整ym(移动中央子午线),综合抵消两项改正变形。
根据上述做法,假设R=6 371 km,在高差变化较小的平坦地区,选择测区平均高程面作为投影面时(即Hm=H0),如果要使投影变形的绝对值小于2.5 cmkm,即变形比例小于140 000,通过式(8)可算出横坐标ym的经差取值范围为[1°42′,1°49′]或[-1°49′,-1°42′],即在中央子午线东西两旁各有一块带状区域满足长度投影变形限值。
对于港口与航道工程,由于港址大多选择在沿海近岸地区,尽管部分区域位于岛屿上(如洋山港与舟山港等),但码头与后方堆场的高差基本很小,为消除投影变形不能采用抵偿面(改变Hm)的方法,而是只能采用平移中央子午线(改变ym)的方法来消除投影变形的影响。至于航道工程高差变化更小,也只能采用平移中央子午线来建立坐标系。
2)本文根据工程范围中心点的地面比例因子,整体缩放测量控制网,获得近似于国家坐标系的独立坐标,从而消除投影变形。
采用工程测量规范消除投影变形方法所建立的坐标系,虽然消除了投影变形,使施工放线能够满足规范的精度要求,但其坐标数值与国家坐标系的数值相差较大,与已有规划图纸拼接使用麻烦(经图纸换算),也不容易被非专业人士理解和使用。本文提出一种更为容易消除变形的方法,就是采用工程范围中心点的地面比例因子对整个控制网进行缩放(控制网必须覆盖整个工程范围)。选定控制网的中心控制点为投影中心,其地面比例因子m的计算公式[6]为:
m=DD0
(9)
通过式(9)计算所得m,或通过软件获取(如天宝的TBC软件),结合其他边长在参考椭球面的投影长度,缩放计算出各控制点的坐标,虽然各控制点位置较国家标准坐标有一定的偏差,甚至达到数米级,但是整体坐标数据变化不大,满足工程施工的规范要求,且与邻近小比例尺图拼接时误差可以忽略不计。
4 工程案例分析
4.1 实例1
刚果(布)黑角新港一期工程位于刚果(布)西部沿海的南端,濒临大西洋的东侧,在原黑角港西北侧,测图采用的平面坐标系统为CONGO 60坐标系,中央子午线经度为9°E(Zone-32),投影方式采用UTM投影,参考椭球为克拉克 1 880 IGN,测区中心位置概略经度为11°48′(与中央子午线经差为2°48′),测区平均高程约5 m。按上述参数进行UTM投影建立平面坐标系统,根据式(8)计算可得测区中心位置边长平均变形量为73 cmkm,远大于规范要求投影变形限差2.5 cmkm的要求,可直接判定采用国家坐标系不能满足设计与施工的精度要求,必须进行换带计算或采用独立坐标系统。调阅资料发现,2013年承接的刚果(布)黑角新港一期工程建立了一套港区独立坐标系(北向坐标为A,东向坐标为B),并提供港区独立坐标系与CONGO 60坐标系(北向坐标为X,东向坐标为Y)之间的换算关系,通过使用该港区的独立坐标系以及其与CONGO 60坐标系换算关系,确保测量成果能够满足设计与施工的精度要求。
4.2 实例2
圣多美集装箱码头一期工程可行性研究阶段测量,目的是为港址选择、码头设计提供高精度的地形图资料。考虑到非洲地区普遍采用UTM投影方式建立坐标系统,故本工程也优选UTM投影。在选择UTM标准分带投影时,中央子午线应当选定为9°E(Zone-32),参考椭球选择WGS-84椭球,但由于本次工程测区中心位置经度为6°40′E(与中央子午线经差为-2°20′),故不能直接采用9°E为中央子午线进行UTM投影建立坐标系。又由于找不到其他基础测绘资料,为满足设计与施工的要求与使用方便,在具体实施时建立了两套坐标系,一套为高斯投影坐标系(L0=6°40′E),供设计与施工使用,另一套为标准UTM投影坐标系(L0=9°E),供将来收集到基础资料后进行转换或者与周边测图拼接使用,表1为投影长度变形消除前后对比,分析可知,采用工程测量规范中的方法可以消除投影变形。
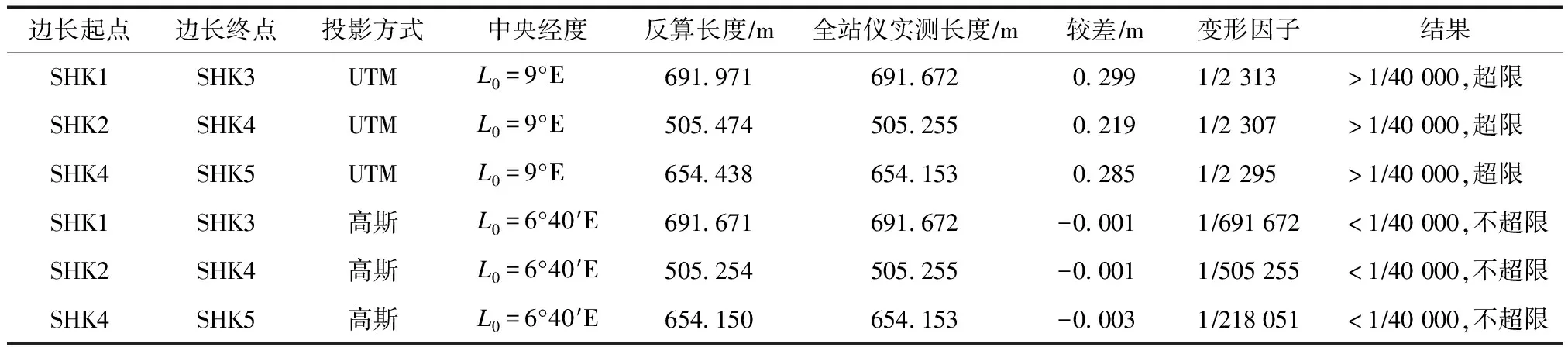
表1 坐标反算长度与全站仪实测长度检核对比
4.3 实例3
孟加拉巴里萨尔市 2×350 MW燃煤电站工程地形测量,目的是为电厂选址、码头设计提供高精度的地形图资料,工程中心经度约为90°4′E。孟加拉国家坐标系统是采用UTM投影方式,带号为46,即L0=93°E。本项目GPS控制网见图2。
该项目若采用标准国家坐标系,坐标反算长度较实际的变形量远远超过规范要求,故为了消除投影变形,又确保坐标数值与国家坐标系接近,本项目坐标系采用本文提出的方法建立,坐标值差异见表2。
采用F017为投影中心,投影所得各点坐标反算长度与全站仪实测长度进行比较,见表3,所有边长均不超限,满足后期工程施工的需要。

注:GPS222和GPS5898为国家基准点,其他GPS点是新布设的控制点。
图2 GPS控制网

表2 似国家坐标系与国家坐标系的坐标值差异

表3 坐标反算长度与全站仪实测长度检核对比
5 结语
1)本文给出UTM投影变形的定量分析公式,并给出两种消除变形的有效方法。
2)对于海外工程,其测区中心位置与国家或原有坐标系统的中央子午线的经差在[1°42′,1°49′]或[-1°49′,-1°42′]时,可以采用国家坐标系或者原有坐标系统进行设计与施工,否则必须进行换带计算或者建立独立坐标系。同时,可以把经差范围作为判别海外工程项目是否需要消除投影变形的简易方法。
3)当采用独立坐标系时,可以采用变化投影方式或者平移中央子午线的方式构建,但坐标值与原国家坐标系相差较大;也可以采用似国家坐标系的方式构建,坐标值与原国家坐标系相差很小;此外还可以采用高斯投影构建独立坐标,在使用过程中比较方便,适用于国内的测绘仪器和软件,且中央子午线经度选择测区的中心位置经度,容易理解。
