基于静力触探CPT测试数据的轨道基础沉降分析

何维维

(中交第三航务工程勘察设计院有限公司，上海 200032)

静力触探作为一种原位测试方法，与常规的勘探和标准贯入等原位测试方法相比，具有测试快捷、经济和节省人力等优点，在国外岩土工程勘察中得到广泛应用。虽然我国在静力触探研究领域取得了一些成果，但技术水平仍停留在科研阶段，与发达国家仍然存在理论研究、应用范围等技术层面上的差距[1]。

在集装箱码头重箱堆场，轨道式龙门吊行驶作业时，需要铺设专用轨道，而轨道基础对地基的沉降及其差异沉降非常敏感。目前国内主要结合勘探及室内土工试验数据确定土体压缩模量，采用传统基础沉降计算方法对轨道基础沉降进行分析，但此方法无法满足国外项目的设计需求，因为通过室内试验测定土体压缩模量值的费用较昂贵，且取样过程中的扰动往往造成得出的数值并不是很准确。如何从理论上解释实际工程中静力触探试验数据结果，并直接应用国外静力触探测试结果对轨道基础沉降变形进行计算分析，是本项目面临的主要技术问题。

1 轨道基础沉降计算理论

1.1 砂土静力触探机理

中东某集装箱码头工程陆域回填采用吹填砂形成，通过将静力触探试验参数与砂土的相对密度和变形等指标建立关系，可快速获得砂土地基的关键参数，具有重要的工程实践意义。但在不同相对密度的砂土中,静力触探的影响范围各不相同,砂土中应力状态、颗粒胶结情况、砂土应力历史、砂土压缩性等参数对静力触探试验结果的影响也不尽相同。因此,砂土静力触探机理无法用统一的数学模式来描述[2]。

Robertson和Campanella总结了Schmertmann等前人研究的试验结果,发现砂的压缩性对锥尖阻力的影响较大，见图1[3]。在相同的竖向有效应力和相对密度Dr的条件下,砂的压缩性越低其锥尖阻力越大。根据已有的文献资料[4]，可得正常固结无黏性土的锥尖阻力qc和相对密实度Dr之间的关系曲线，见图2，可根据有效压力及锥尖阻力值得到砂土的相对密实度Dr。

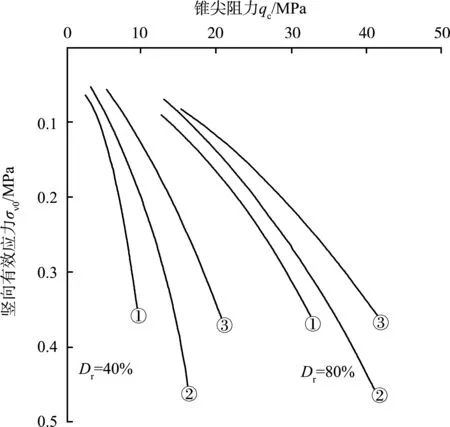
注：①线为Schmertmann使用高压缩性的砂试验得出的结果;②线为Baldi使用中等压缩性的砂试验得出的结果;③线为Villet和Mitchell使用低压缩性的砂试验得出的结果。

图1 砂的压缩性对静力触探锥尖阻力的影响

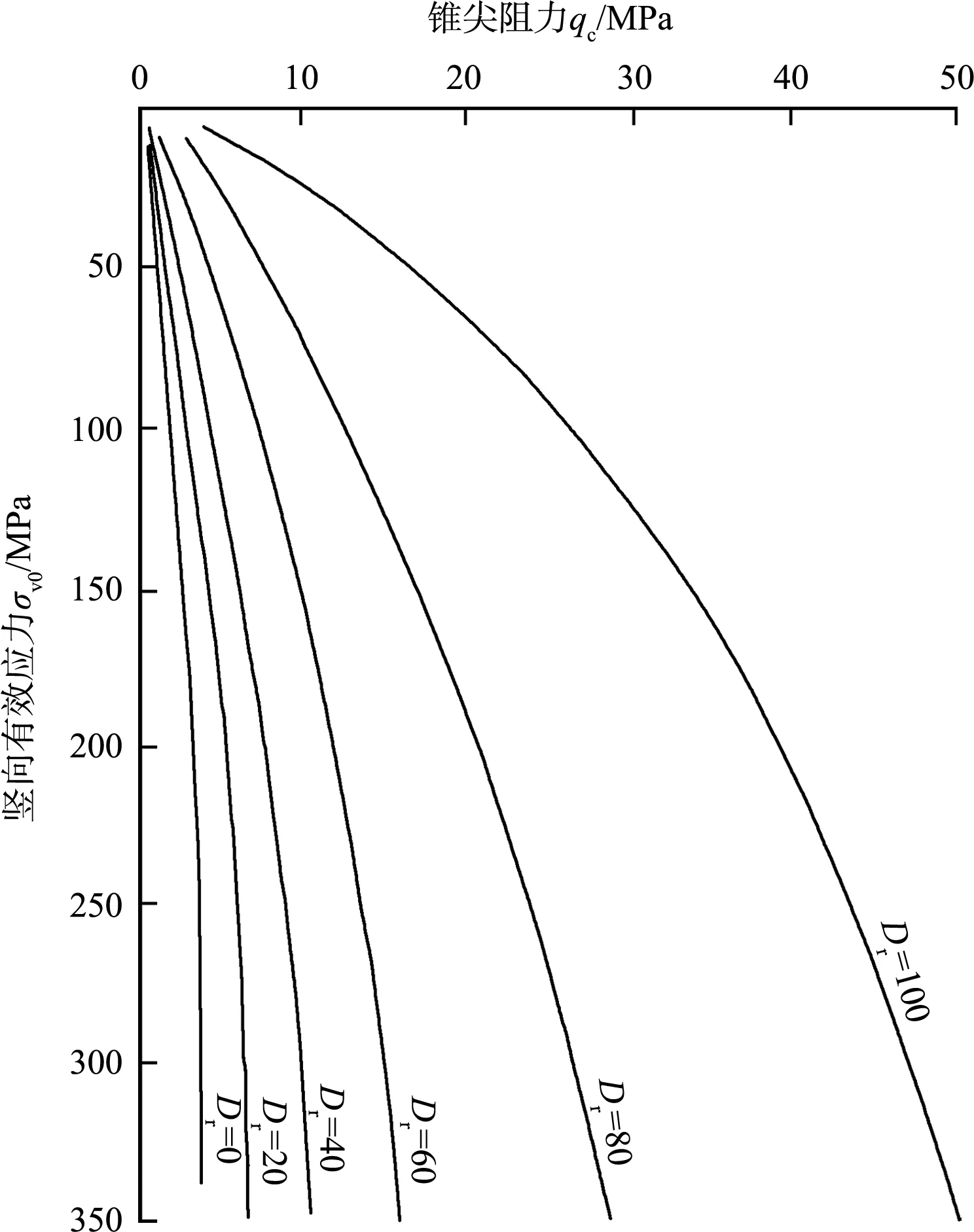
图2 正常固结无黏性土的qc和Dr近似关系

1.2 轨道基础沉降计算公式

Schmertmann提出采用一个三角形的相对应变图来模拟应变的分布，此图形的面积与沉降量有关。根据应变剖面图，求出每个不同压缩模量E的深度增量范围中部的影响系数Iz，并考虑基础埋置深度和时间的影响，基础总沉降s计算公式如下：

(1)

(2)

(3)

C2=1+0.2lg(10t)

(4)

式中：Iz为土体应变影响系数；Ei为第i层土体压缩模量；n为总层数；Δzi为基底下土层分层厚度，一般取0.5 m；Δp为基底附加应力；Izp为土体应变影响系数的峰值；σv0为对应基础埋置深度处的地基土体初始有效自重应力(kPa)；σ′2为Izp所在深度处的地基土体初始有效自重应力(kPa)，条形基础，Izp所在深度为B，独立基础，Izp所在深度为B2；C1为埋置深度影响系数；C2为蠕变影响系数；t为运营后时间，一般取1 a；C3为基础类型影响系数，对于条形基础，C3为1.75，对于方形基础，C3为1.25。Schmertmann方法应用于砂土地基上条形基础沉降计算见图3。

注：B为条形基础宽度(m)；D为条形基础埋深(m)；q为基础结构上部荷载(kPa)。

图3 Schmertmann方法应用于砂土地基上条形基础沉降计算

轨道基础差异沉降可采用相邻两点之间的沉降量差值来计算，它的大小可按计算所得最大总沉降量的34进行估算。

2 工程实例

2.1 工程概况

中东地区某集装箱码头工程主要为原有汽车、杂货堆场改建为半自动化集装箱专业码头，陆域堆场总面积约67.8万m2，重箱堆场装卸工艺采用轨道式龙门起重机，见图4。

图4 中东某集装箱码头改造项目卫星图

根据本工程P5、P6区地基处理交工报告显示，工程采用海砂吹填造地，吹填砂层平均厚度约12 m，吹填层以砂、砾为主，细粒土含量低。吹填砂层经过振冲或强夯法加固，表层砂较密实，地基处理后进行了沉降计算分析，该区域场地在大面积使用荷载50 kPa均载作用下，总沉降值在50 mm以内，见图5。

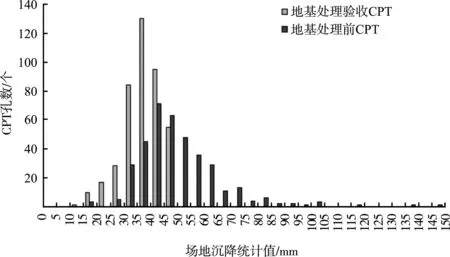
图5 P5及P6区沉降计算值

2.2 设计荷载

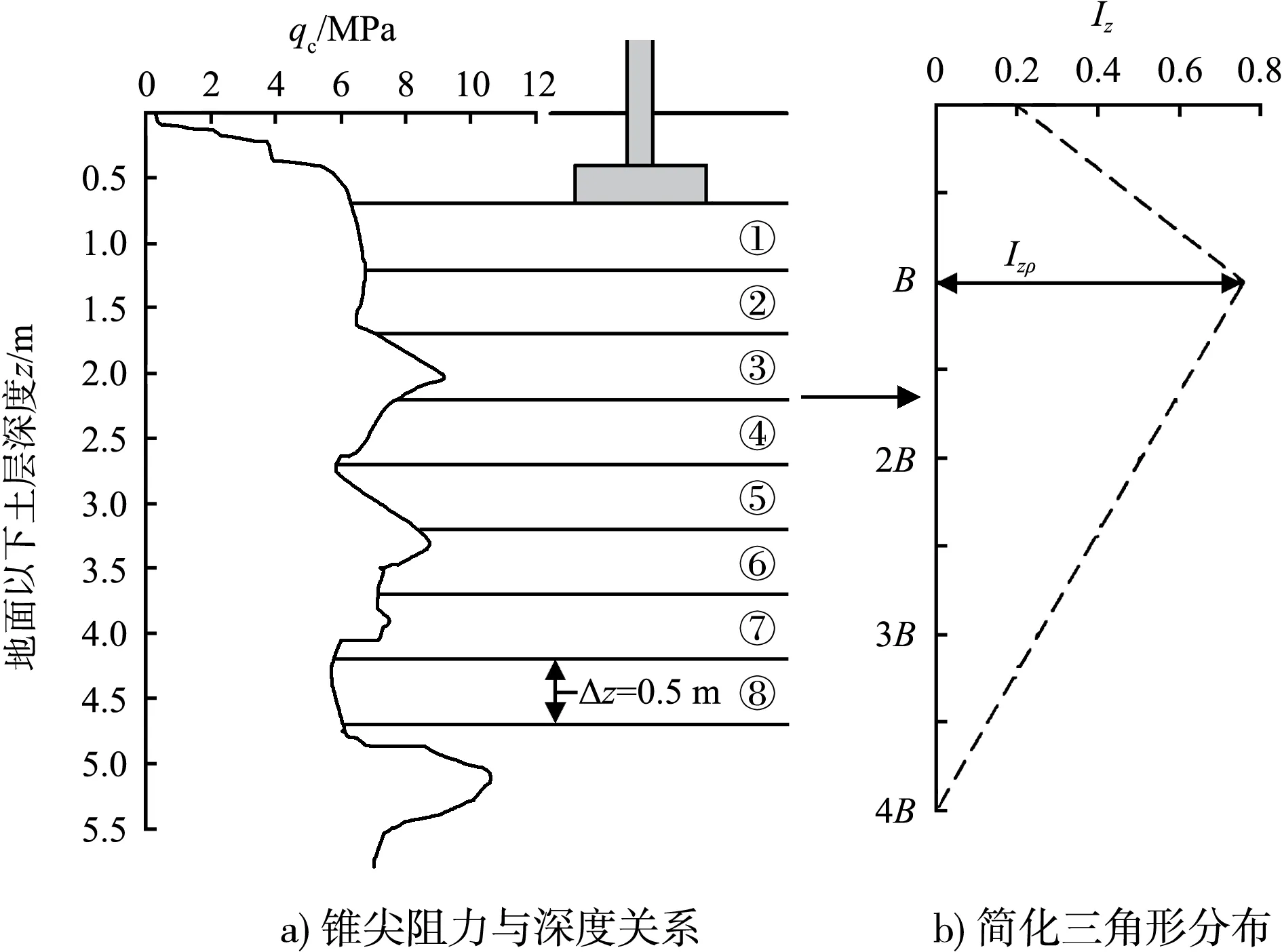
轨道上主要运行自动化轨道龙门吊，轨距34 m、基距17 m、轮距1.05 m，每支腿4轮，最大轮压340 kPa。根据轨道式龙门吊行走轨道所允许偏差，轨道基础沉降要求控制为：使用期内，同一截面不均匀沉降

2.3 基础沉降计算分析

根据项目设计报告，静力触探锥尖阻力qc与砂土压缩模量E的关系为E=3qc，见图6。

图6 锥尖阻力qc与砂土压缩模量E关系

轨道基础分段长度L为30 m，轨道基础宽度B为2.2 m，基础埋深为0.83 m，轨道基础为条形基础。根据设计荷载及Schmertmann计算公式，基底以下土层按0.5 m进行分层，见图7，读取静力触探原位试验的锥尖阻力qc。经计算，基底附加应力Δp为155.4 kPa，Izp为0.66，条形基础的基底应变影响系数Iz简化为三角形分布，z为地面以下土层深度(m)。

(5)

Iz=0.4B-0.1z(B

(6)

图7 基础沉降Schmertmann方法计算简图

根据本项目P5[6]及P6[7]区地基处理交工报告中静力触探CPT测试数据，选取P5及P6区一些代表性静力触探孔。采用Schmertmann方法计算在轨道使用荷载作用下轨道基础总沉降，沉降计算值见图8。

图8 轨道基础沉降计算值

砂土地基上轨道基础最大总沉降为13 mm，轨道基础差异沉降按总沉降34估算，小于10 mm。同时轨道基础采用弹性地基梁结构，可调式柔性轨道固定系统后期轨道可调节高度为100 mm，完全可覆盖所有工后沉降量，因此轨道基础设计采用弹性地基梁结构可调式柔性轨道固定系统。由于地基沉降不均匀造成钢轨顶面高差时，可以通过钢轨的固定系统来进行钢轨竖直方向的调整，使得钢轨的轨道顶面高程满足运营期正常使用要求。

3 结论

1)Schmertmann方法直接应用静力触探测试结果对轨道基础沉降变形进行计算分析，计算公式简单，物理意义明确。计算公式中所需参数可通过静力触探测试数据直接获取，无须室内试验及钻探取样，降低了勘探测试成本及周期，而且也满足境外工程设计审查要求。

2)Schmertmann方法基于对文献中的大量工程实例进行计算，计算所得的沉降值与实测值相当吻合，结合本项目P5及P6区沉降计算统计值对比分析，计算效果良好，满足轨道基础的国际设计标准。

3)各向异性、应力历史、自然胶结作用以及超固结状态很可能是影响土体压缩模量的十分重要的因素，而对无黏性土尤其如此。该方法仅考虑正常固结砂土，对于超固结砂土，在沉降成为设计必须考虑的因素之一时，应仔细查明场地条件。