T 形截面部分包覆钢-混凝土组合梁抗弯刚度及承载力试验研究

肖 锦 李 杰 陈以一

（同济大学土木工程学院建筑工程系，上海200092）

0 引 言

部分包覆钢-混凝土组合梁（partially encased composite beams，简称PEC梁）是由工字钢或H型钢（轧制或焊接）及填充在钢翼缘之间的混凝土组成，通常在型钢腹板处焊接栓钉或钢筋作为抗剪件，以保证钢梁与混凝土间的整体作用，其典型截面形式如图1（a）所示。若钢梁顶部带有翼板，则截面形式如图1（b）所示，钢梁与翼板间通常采用栓钉连接。本文将两种截面形式PEC梁分别称为矩形截面PEC梁及T形截面PEC梁。

PEC梁在结构性能和经济性方面具有显著优势。与钢梁相比，具有更好的刚度、承载力以及抗火、抗腐蚀性能；与混凝土梁相比，可以有效降低截面高度，同时提高建筑预制装配化程度。目前国外对PEC梁的研究较为成熟，加拿大和欧洲已将PEC构件纳入相关设计规范，欧洲规范《EN 1994-1-1：2004》（以下简称欧规4）中提出了矩形截面PEC梁抗弯刚度和承载力的计算方法［1］。国内赵荣桥［2］、胡夏闽等［3］也进行过矩形截面 PEC梁抗弯性能方面的研究。

图1 两种截面形式PEC梁Fig.1 Two section forms of PEC beams

目前国内外对于T形截面PEC梁的研究较少，为此本文通过试验研究T形截面PEC梁的抗弯性能，并以此验证本文提出的抗弯刚度和承载力计算方法。

1 试验概况

1.1 试件制作

两个T形截面PEC梁试件编号分别为TPEC-1和TPEC-2。截面如图2所示，为考察不同截面构造形式对抗弯性能的影响，试件TPEC-1采用对称翼缘型钢，尺寸为240×180×6×10；试件TPEC-2则采用非对称翼缘型钢，尺寸为240×180（120）×6×10，其中括号内为型钢上翼缘宽度。

图2 试件截面构造Fig.2 Section structure of test piece

腹部混凝土纵向受拉钢筋为4C10，箍筋为B6@150。混凝土翼板尺寸为600×100，两个方向配筋均为B6@100。混凝土均采用C30，型钢均采用Q235-B。

欧规4中规定：PEC梁中应设置栓钉等连接件或者横向钢筋以保证钢梁与混凝土共同作用［1］。本试验栓钉均采用M13，沿梁长方向布置。为保证完全抗剪连接，参考《组合结构设计规范》（JGJ 138—2016）［4］，按照无腹部混凝土的普通钢-混凝土组合梁计算：式中：Vs为每个剪跨区段内钢梁与翼板交界面的纵向剪力；Ncv为一个抗剪连接件的纵向抗剪承载力；

混凝土翼板与钢梁交接处的栓钉间距设为100 mm，此时为完全抗剪连接。有试验结果表明［5］，腹部仅靠自然粘结的PEC梁，在承载力极限状态下，滑移量依旧很小，故腹部栓钉间距设为200 mm。栓钉布置图如图3所示。

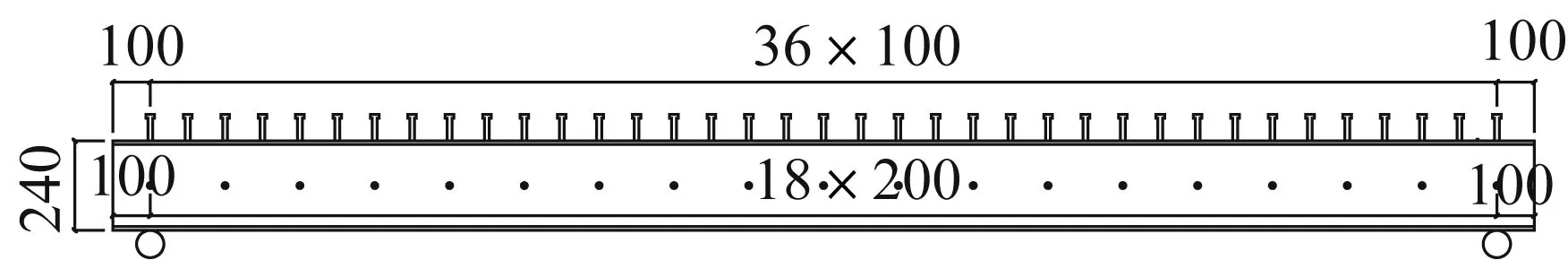
图3 栓钉布置图（单位：mm）Fig.3 Stud layout（Unit：mm）

1.2 材料性能

混凝土分三次浇筑：对于腹部混凝土，仅在梁端支模，先浇筑一侧，待终凝并养护一段时间后，翻面再浇筑另一侧，最后支模浇筑混凝土翼板，浇筑日期见表1。

表1 混凝土浇筑日期Table 1 Date of concreting

三次浇筑各预留了12块试块，其中6块尺寸为150 mm×150 mm×150 mm，用于测量混凝土抗压强度fcu；剩余6块尺寸为150 mm×150 mm×300 mm，用于测量混凝土静力受压弹性模量Ecu。试验结果见表2。

表2 混凝土材料性能Table 2 Properties of concrete materials

本试验均采用轧制型钢梁截面，钢材均为Q235，纵向钢筋均采用HRB400。钢板取样厚度分别为6 mm和10 mm（经验算，厚度对承载力及刚度计算基本无影响，故此处均采用名义厚度），钢筋取样直径为10 mm，箍筋不进行材性试验。试验结果见表3。

表3 钢材材料性能Table 3 Properties of steel materials

1.3 加载装置及测点布置

采用四点弯曲加载方式，200 t位移控制作动器。加载时，先力控制加载后位移控制加载。每一级加载15 kN，加载速度为15 kN∕min，达到预估极限承载力的0.5倍后，调整为位移加载控制，每一级加载0.5 mm，加载速度为0.5 mm∕min，加载至构件破坏。试验加载装置及加载照片见图4。

图4 加载装置及加载照片（单位：mm）Fig.4 Loading device and photo（Unit：mm）

试验测量内容包括：①试件跨中挠度；②腹部混凝土及翼板的开裂和裂缝发展；③跨中截面混凝土拉、压应变，钢筋和型钢应变；④腹部混凝土及翼板与钢梁间的相对滑移。位移计及应变片测点的布置如图5所示。

其中W1-W3用以测量跨中挠度；W4-W6用以测量腹部混凝土与钢梁的相对滑移，实际布置如图5（c）所示，位移计固定于钢梁下翼缘，在腹部混凝土表面粘连角钢以量测两者相对位移；W7-W9用于量测翼板与钢梁间的相对滑移，实际布置如图5（c）所示，位移计固定于钢梁上翼缘，在翼板下表面粘连角钢以量测两者相对位移。YC表示混凝土应变片，YS表示钢梁应变片。钢筋应变片预埋在构件中。

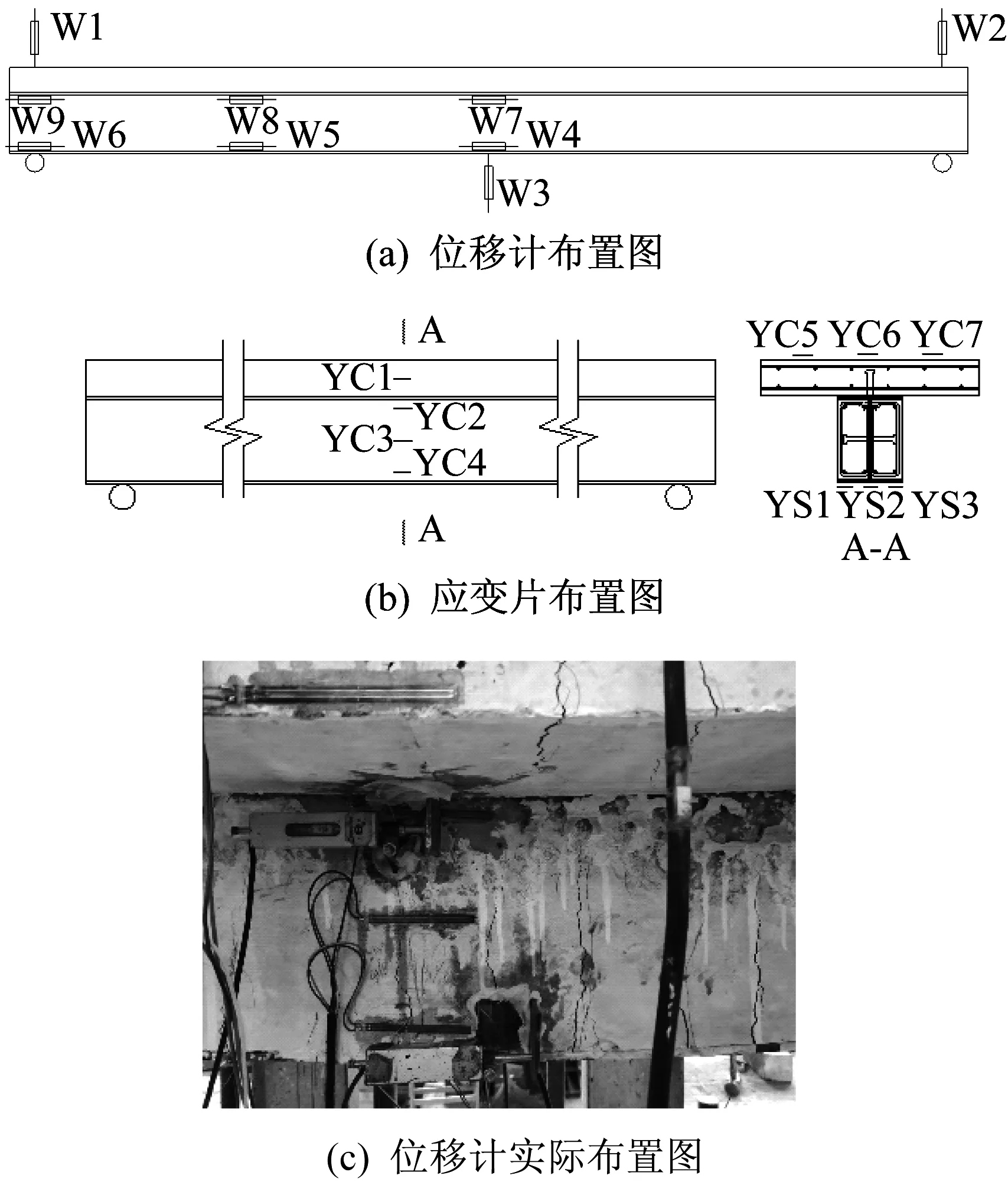
图5 位移计及应变片布置图Fig.5 Layout of displacement meter and strain gauge

2 试验结果与分析

2.1 试验现象

试件 TPEC-1：加载至 105 kN（0.25Pu），南侧（先浇筑侧）开裂，纯弯段和剪跨段均出现细微裂缝；加载至135 kN（0.32Pu），北侧开裂，剪跨段开始出现裂缝，此时南侧已累计出现8条裂缝；加载至 211 kN（0.5Pu），跨中挠度为 7.5 mm（l∕460），受拉区最大裂缝宽度为0.13 mm；加载至295 kN（0.7Pu），跨中挠度为13.0 mm（l∕308），受拉区最大裂缝宽度为0.16 mm；加载至315 kN（0.75Pu），型钢受拉翼缘屈服，此时构件刚度开始逐渐下降，跨中 挠 度 为 14.5 mm（l∕276）；加 载 至 345 kN（0.82Pu），纵向受拉钢筋屈服，此时裂缝宽度增加显著，跨中挠度为17.7 mm（l∕226）；加载至360 kN（0.85Pu），腹部混凝土裂缝基本出齐并发展至翼板翼缘，同时翼板跨中混凝土开始起皮开裂，跨中挠度为 20.0 mm（l∕200）；加载至 421 kN（Pu），跨中挠度达到80 mm（l∕50），认定构件破坏，此时翼板跨中混凝土开裂明显，考虑到构件整体性较好，继续加载；当荷载下降至400 kN（0.95Pu），挠度达到165 mm（l∕24），此时翼板跨中混凝土压溃明显，终止加载。

试件 TPEC-2：加载至 130 kN（0.30Pu），南侧（先浇筑侧）开裂，纯弯段和剪跨段均出现细微裂缝；加载至145 kN（0.35Pu），北侧开裂，剪跨段开始出现裂缝，此时南侧已累计出现12条裂缝；加载至209 kN（0.5Pu），跨中挠度为 7.9 mm（l∕506），受拉区最大裂缝宽度为0.14 mm；加载至292 kN（0.7Pu），跨中挠度为13.2 mm（l∕303），受拉区最大裂缝宽度为0.23 mm；加载至310 kN（0.74Pu），型钢受拉翼缘屈服，此时构件刚度开始逐渐下降，跨中挠度为14.8 mm（l∕270）；加载至360 kN（0.86Pu），纵向受拉钢筋屈服，此时裂缝宽度增加显著，跨中挠度为 20.8 mm（l∕192）；加载至417 kN（Pu），跨中挠度达到80 mm（l∕50），认定构件破坏，考虑到构件整体性较好，继续加载；当荷载下降至315 kN（0.76Pu），挠度达到168 mm（l∕24），此时翼板跨中混凝土压溃明显，终止加载。

观察破坏后的构件，翼板加载点附近破坏较为严重，但未明显掉落，整体性较为完好。腹部混凝土与钢梁端部交界面未发现水平裂缝，可认为两者间相对滑移较小。翼板与钢梁之间出现较明显相对滑移。凿开翼板及腹部混凝土，型钢受压翼缘未产生局部屈曲。部分试验现象及破坏模式见图6。

图6 试验现象及破坏模式Fig.6 Test phenomenon and failure mode

2.2 跨中荷载-挠度曲线

跨中荷载-挠度曲线见图7，与普通组合梁类似，T形截面PEC梁的受力状态可以分为弹性段、弹塑性段和下降段。弹性阶段（P≤0.75Pu），随着荷载增加，腹部混凝土出现裂缝，由于钢梁约束，裂缝发展缓慢，刚度未明显下降，故曲线基本呈现线性变化。弹塑性阶段（0.75Pu≤P≤Pu），型钢受拉翼缘及纵向受拉纵筋先后屈服，腹部混凝土裂缝发展迅速，截面刚度逐渐降低，跨中挠度的增加速率远超过荷载的增加速率，故曲线呈现非线性变化。下降段（P≥Pu），荷载缓慢下降，但挠度仍有较大发展，表明构件延性较好。

跨中挠度90 mm（l∕44）附近，两个构件的翼板跨中混凝土均开始压溃，逐渐退出工作，导致荷载产生突降。TPEC-1 在挠度 120 mm（l∕33）左右荷载发生反弹，因为此时翼板已全部退出工作，中和轴下移至钢梁腹板中，钢梁及腹部混凝土截面受压区面积增大，导致承载力提升。而TPEC-2采用非对称翼缘型钢导致钢梁受压区面积小于TPEC-1，且试验过程中翼板破坏程度小于TPEC-1，此时翼板尚未退出工作，故承载力未发生反弹。

此外TPEC-2的抗弯承载力为417 kN，与TPEC-1的421 kN相近，且两者曲线发展趋势一致，表明本试验所采用的非对称翼缘型钢截面构造方式对抗弯承载力影响不大。

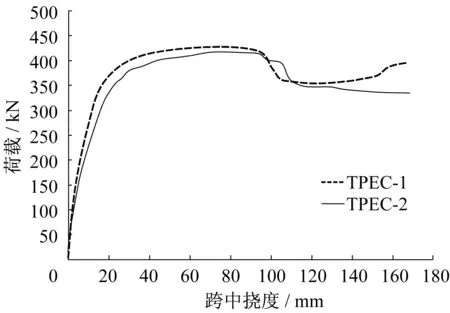
图7 跨中荷载-挠度曲线Fig.7 Midspan load-deflection curve

2.3 型钢应变发展情况

荷载-型钢应变曲线见图8，在加载初期，随着荷载上升，型钢应变基本呈现线性上升。当荷载达到（0.75～0.77）Pu时，型钢开始屈服，应变曲线开始出现拐点，之后应变迅速增大。与跨中荷载-挠度曲线的发展趋势相吻合。

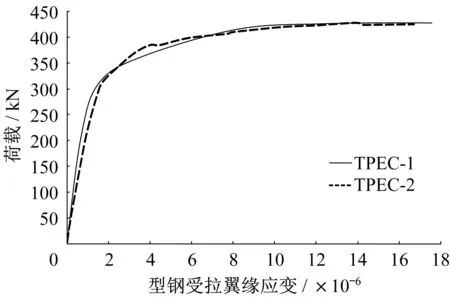
图8 荷载-型钢应变曲线Fig.8 Load-steel strain curve

2.4 跨中截面混凝土应变发展

跨中截面混凝土各高度处应变如图9所示，其中h表示距离最下侧混凝土应变片的高度。可以看出跨中截面应变沿高度近似呈现线性分布，基本符合平截面假定。

图9 跨中截面应变分布Fig.9 Strain distribution of midspan section

2.5 混凝土滑移情况

加载至极限荷载时，三处位置的最大滑移值见表4。其中腹部混凝土与钢梁间的滑移（S1）在梁端最大仅为0.028 mm，跨中最大为0.942 mm，因为正弯矩作用下，跨中腹部混凝土开裂较大，而端部裂缝较少，使得跨中相对滑移大于梁端。故总体来说，两者间的滑移量较少，在计算时可不予考虑。

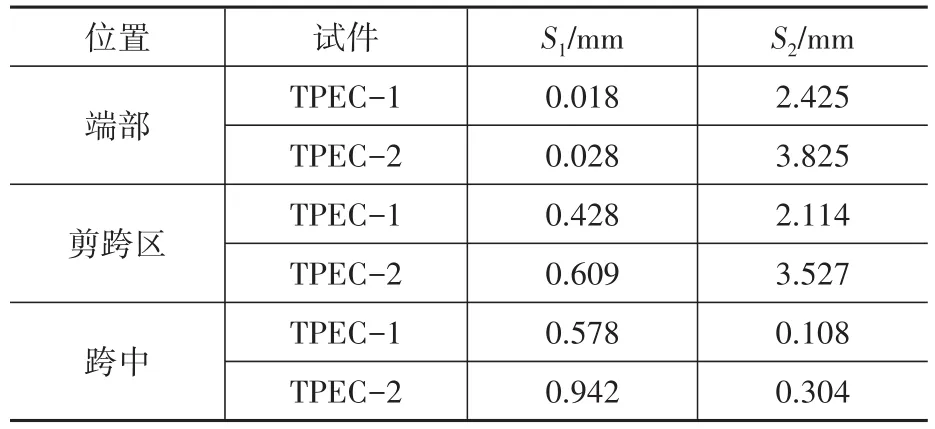
表4 三处位置的最大滑移值Table 4 Maximum slip at three locations

翼板与钢梁间的最大滑移（S2）则在梁端较大，跨中较小，但并不为零，表明在剪应力为零的纯弯段栓钉水平剪力并不为零［5］。总体来说，两者间相对滑移较大，在计算时须考虑滑移对刚度的影响。且TPEC-2翼板与钢梁间的最大滑移值均大于TPEC-1，表明非对称翼缘型钢的截面构造方式，由于受压翼缘与翼板有效接触面积减小，且翼板承担了更多压应力，使得混凝土与钢梁间的相对滑移有增大趋势。

2.6 腹部混凝土的裂缝宽度

正常使用阶段的荷载通常为试验极限荷载的0.3～0.7倍，通过电子裂缝测宽仪记录下了0.3Pu、0.4Pu、0.5Pu、0.6Pu和 0.7Pu下的最大裂缝宽度，计算出平均裂缝宽度，并进行横向比较，见图10。可以看到，随着荷载增加，平均裂缝宽度以及最大裂缝宽度均呈现增加趋势，但未超过正常使用阶段0.3 mm的限值［6］。此外TPEC-2的最大裂缝宽度均大于TPEC-1，表明非对称翼缘型钢的截面构造方式，由于型钢受压翼缘面积减小，导致腹部纵向钢筋承担更多拉应力，使得正常使用阶段的腹部混凝土裂缝宽度有增大趋势。

3 截面受弯承载力计算

3.1 全塑性理论

全塑性理论计算T形截面PEC梁受弯承载力的基本假定如下：①截面应变分布满足平截面假定；②翼缘和腹板钢梁与混凝土之间相对滑移很小，可忽略不计；③混凝土压应力呈矩形分布，达到轴心抗压强度；④钢梁在受拉或受压区的应力均达到钢材的抗拉或抗压屈服强度；⑤下部纵向钢筋应力达到屈服强度，不计上部纵向钢筋的作用；⑥忽略受拉区混凝土的作用［4］。

3.2 受弯承载力计算公式

T形截面PEC梁计算简图见图11，其中be、hc分别为翼板的有效宽度及高度；ha、bf分别为钢梁截面高度及翼缘宽度；x为塑性中和轴至混凝土受压边缘的距离；y1为钢梁截面应力的合力至塑性中和轴的距离；as为受拉区钢筋合力点至混凝土受拉边缘的距离。

图10 腹部混凝土的裂缝情况Fig.10 Cracks in concrete of abdomen

图11 受弯承载力计算示意图Fig.11 Calculation diagram of bending capacity

按照全塑性理论计算受弯承载力会出现以下三种计算情况，见图12。

1）中和轴位于翼板内（图12（a））

式中：tf为钢梁受拉翼缘厚度；fy、fa分别为钢筋、钢梁抗拉强度设计值；fc为翼板混凝土抗压强度设计值；As为受拉钢筋截面面积；Aa为钢梁全截面截面面积；α1为受压区混凝土压应力影响系数，当混凝土强度等级不超过C50时，α1取1.0，当混凝土强度等级为C80时，α1取0.94，其间按线性内插法确定。

图12 三种计算情况Fig.12 Three cases of calculation

2）中和轴位于钢梁上翼缘内（图12（b））

式中：f‘a为钢梁抗压强度设计值；Aac为钢梁抗压区截面面积；Sat、Sac分别为钢梁受拉区和受压区对塑性中和轴的面积矩；其余同上。

3）中和轴位于钢梁腹板内（图12（c））

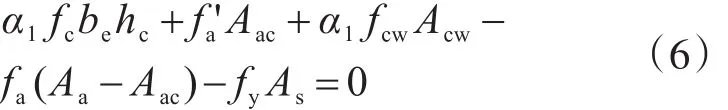
式中：fcw为腹部混凝土抗压强度设计值；Acw为腹部混凝土受压截面的面积，t'f为钢梁受压翼缘厚度；其余同上。

3.3 与试验结果比较

将跨中极限弯矩理论值与试验值对比，见表5，M为试验值（极限荷载Pu对应的跨中弯矩），M1为理论值。可以发现两者吻合较好，采用上述全塑性理论计算T形截面PEC梁受弯承载力是安全合理的。对本试验而言，翼板与钢梁间相对滑移对承载力的减弱被钢梁的强化效应所抵消，故承载力接近。

表5 理论值与试验值对比Table 5 Comparison between theoretical and experimental value

4 截面抗弯刚度计算

4.1 现有计算方法

4.1.1 换算截面法

换算截面法被许多国家规范所采用，该方法基于以下假定：①钢和混凝土材料均为理想的线弹性体；②钢和混凝土间保证完全共同作用。将两种材料按照强度等效原则，换算成单一的材料计算截面惯性矩［7］。但是从本试验可知，对于T形截面PEC梁翼板与钢梁间会产生一定相对滑移，所以按换算截面法计算可能会导致截面刚度偏大而偏不安全。此外未考虑腹部混凝土开裂的影响。

4.1.2 平均刚度法

欧规4认为腹部混凝土由于开裂并不能完全对PEC梁刚度起到作用，所以以换算截面法为基础，取考虑受拉区混凝土作用的截面刚度和不考虑受拉区混凝土作用的截面刚度的平均值（均不考虑受压钢筋的作用），作为T形截面PEC梁的抗弯刚度［1］，本文将此方法简称为平均刚度法，即

式中：Iucr为考虑受拉区混凝土作用的换算截面惯性矩；Ier为不考虑受拉区混凝土作用的换算截面惯性矩。但欧规4同样未考虑交界面滑移对刚度的影响。

4.1.3 折减刚度法

我国《钢结构设计标准》（GB 50017—2017）［8］为考虑滑移对组合梁抗弯刚度的影响，在换算截面法的基础上，引入刚度折减系数ξ对弹性刚度进行折减。但对于T形截面PEC梁构件，此方法未考虑腹部混凝土开裂的影响。

4.1.4 折减平均刚度法

为考虑腹部混凝土开裂和交界面滑移的影响，本文将平均刚度法和折减刚度法相结合，即得到较为合理的T形截面PEC梁抗弯刚度计算公式，其中ξ参照《钢结构设计标准》（GB 50017—2017）［8］中的计算公式，即

4.2 与试验结果比较

将四种方法的挠度计算值与试验结果对比，见表6，其中，f为实测挠度，f1为采用换算截面法计算的挠度，f2为采用平均刚度法计算的挠度，f3为采用折减刚度法计算的挠度，f4为采用折减平均刚度法计算的挠度。分别取0.5Pu和0.7Pu作为正常使用极限状态对应的荷载。可以发现，换算截面法和平均刚度法由于忽略了交界面滑移的影响导致挠度偏小，偏不安全；折减刚度法未考虑腹部混凝土开裂的影响，挠度值同样偏小，而折减平均刚度法的计算结果与试验实测值吻合较好。

表6 理论值与试验值对比Table 6 Comparison between theoretical and experimental value

5 结 论

通过两根T形截面PEC梁的试验得出以下结论：

（1）T形截面PEC梁具有良好的延性和变形能力。达到极限荷载时，型钢受拉翼缘和腹部纵向受拉钢筋均进入屈服状态，型钢受压翼缘未发生局部屈曲。腹部混凝土与钢梁间的相对滑移较小，可忽略不计。翼板与钢梁间的相对滑移较大，在计算时需考虑对刚度的影响。为减少用钢量采用非对称翼缘型钢的截面构造方式，可能会增加混凝土与钢梁间的相对滑移以及正常使用阶段的裂缝宽度。

（2）全塑形理论计算T形截面PEC梁的受弯承载力是合理的，理论计算与试验值吻合较好。

（3）T形截面PEC梁抗弯刚度应考虑腹部混凝土开裂以及翼板与钢梁相对滑移的影响，可在欧规4计算方法的基础上引入刚度折减系数对刚度进行折减，此方法计算值与试验值吻合较好。