梁的疲劳开裂各向同性弯曲损伤分析

王天风 盛冬发，* 董春雷 齐荣庆

（1.西南林业大学土木工程学院，昆明650224；2.西南林业大学材料工程学院，昆明650224）

0 引 言

疲劳失效是机械工程领域中一类十分普遍的物理现象，它的基本特征为材料在远低于其静强度极限的交变荷载的持续作用下，萌生多种类型的内部缺陷（如位错、滑移、孔洞、微裂纹、应力诱发相变等），并逐步演化成为宏观裂纹，以及由于裂纹扩展而最终导致结构破坏的过程。

据统计，在现代工业各领域，约有80%以上的结构破坏都是由疲劳失效所引发的，所以疲劳问题在航空工业、交通运输、能源工业等领域受到越来越多的重视和关注。对于一般的机械结构来说，疲劳失效的过程可以分为裂纹形成与裂纹扩展两个阶段。对于裂纹形成阶段多采用损伤力学分析方法，对于裂纹扩展阶段多采用断裂力学的分析方法。疲劳裂纹形成阶段的过程，就是损伤演化的过程。人们只需要根据损伤演化发展的规律，就可以把握整个疲劳裂纹形成阶段整个过程。因此，损伤力学已成为解释疲劳裂纹形成阶段的主流方法。

就疲劳损伤问题而言，大多数问题可归结为如何获取在给定载荷谱下构件的使用寿命问题。将连续损伤力学（CDM）应用到疲劳问题中，得到合理的疲劳损伤演化方程，被认为是预测疲劳寿命最有效的方法之一。许多学者对疲劳损伤演化方程的具体形式进行了研究，代表性的有Chaboche［1］首次系统地将CDM方法应用于疲劳寿命的预测中。Lemaitre［2］根据连续损伤力学理论，提出了一种疲劳损伤演化方程。Kim等［3］发展了Chaboche的损伤演化方程，并用于高温下镍基合金的疲劳蠕变寿命预测。Xiao等［4］发展了一个可以考虑平均应力效应的高周损伤演化方程。Bhattacharya等［5］提出了一种估算累积疲劳损伤的连续损伤力学模型，并从热力学基本原理预测裂纹萌生时疲劳寿命。Wang等［6］提出了一种研究弹性体疲劳损伤行为的连续损伤模型，建立了损伤发展方程来预测给定的名义应变振幅循环载荷作用下的疲劳寿命。Dattoma等［7］提出了一种非线性连续损伤力学模型，能较好地预测复杂载荷作用下的疲劳寿命。Schwab等［8］将连续损伤力学（CMD）模型应用于韧带蠕变和疲劳来揭示损伤机制，得到韧带疲劳损伤的机制不同于蠕变损伤。杨锋平等［9］将连续损伤力学应用到疲劳问题中，得到疲劳损伤演化方程可有效地预测疲劳寿命。罗璐等［10］基于连续损伤力学建立了两种疲劳损伤扩展模型，两种模型的计算结果与试验结构吻合良好。

1 疲劳问题的损伤耦合理论

耦合损伤疲劳失效模型的基本方程如下。

1.1 几何方程

小变形的位移与应变关系为

式中，ui与εij分别为位移与应变分量。

1.2 本构关系

考虑损伤的应力-应变关系为

式中：σij为应力分量；cijkl为无损材料的弹性常数；D为损伤变量，对于各向同性材料，损伤变量可被看作标量，同时，0≤D≤1。

1.3 平衡方程

式中，fi为体积力。

1.4 边界条件

1.5 损伤演化方程

引入有效应力：

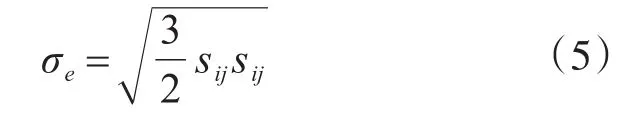
式中，sij为应力偏量分量：

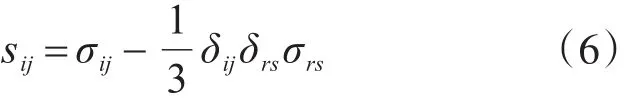
式中，δij为克罗内克符号（Kronecker delta）。

定义为

应用Chaboche和Lemaitre等提出的疲劳损伤演化方程，即：

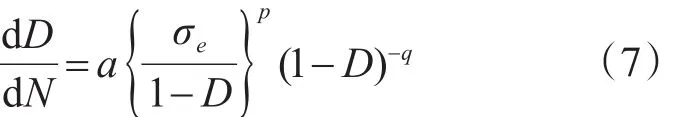
式中，N代表应力循环次数，a、p和q均为材料常数，取决于材料的疲劳性能曲线。需指出，σe应视为应力循环中的广义力；而a则是应力比的函数。

2 梁纯弯曲损伤模型

图1所示为梁的纯弯曲变形模型。梁的宽度为b，高度为h，假设梁是均质的。在纯弯曲载荷作用下材料受到损伤，损伤只在受拉应力区出现，受拉区的损伤为各向同性损伤，并且可以假定沿梁的宽度方向损伤是均匀分布的。由于梁受拉区受损伤影响，承载能力下降，中性轴将向受压区移动，设y0为中性轴偏离横截面中心轴线的距离（图1（a））。

图1 梁的纯弯曲损伤变形模型Fig.1 Damage deformation model of beams under pure bending loads

如果此时梁的平截面假设（Euler-Bernauli假设）仍然成立，则几何关系（简称广义应变等效条件）为

设受压区应力为σc，受拉区应力为σt。单向拉伸的损伤变量D为kachanov各向同性损伤变量，应该说明，这里损伤变量D不但和循环荷载作用次数N有关，还和梁截面上任一点y方向的位置有关。根据Lemaitre应变等效性假设，受压和受拉区应力可分别写为

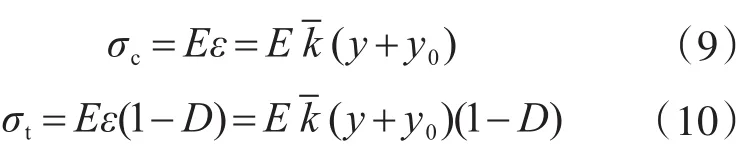
以新中性轴zC为参考轴，列力平衡方程：

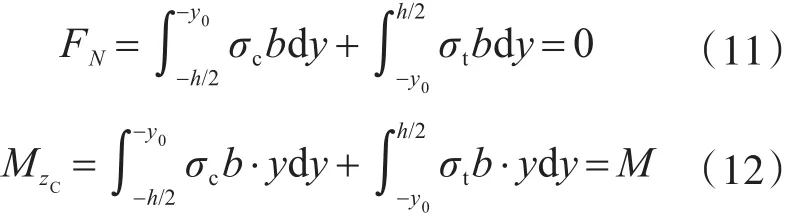
将式（9）和式（10）代入式（11），可得：

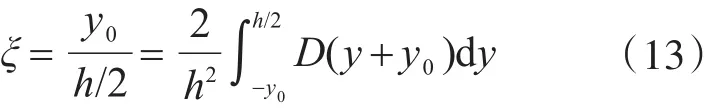
上式表明受损梁中性轴移动的无量纲坐标ξ为材料损伤对中性轴y=-y0的一次矩。将式（9）和式（10）代入式（12），可得：

应用Chaboche和Lemaitre等人提出的疲劳损伤演化方程式（7），并设q=0，参考文献［11］，可将矩形截面梁疲劳损伤演化规律写为

这里，Dm(N)为梁底缘在循环荷载重复作用N次后的损伤量。为了表示方便，记利用参考文献［11］，Dm(N)可表示为

（16a）式也可写为

循环荷载重复作用N次后梁底缘的应变为

式中，εm(0)为梁底缘在循环荷载重复作用N=0次时的应变。

对于梁底缘Dm(N)=Dc时，矩形截面梁的疲劳寿命为式（18）所示。随着循环荷载重复次数的增加，梁受拉区的疲劳损伤不断累积。当梁底缘疲劳损伤值达到损度临界值Dc时，梁处于疲劳裂纹开始形成、宏观裂纹开始扩展阶段。从理论上说，损伤临界值Dc=1，但从试验中发现，损伤临界值Dc往往没有达到1裂纹形成阶段已经结束。在本文中，取损伤临界值Dc=0.5。为了从理论上说明整个疲劳裂纹形成阶段中疲劳损伤值和循环荷载的重复作用次数N的关系，可以对Dm在[0，0.5]区间上五等分点上取值。

为了说明上面这些公式的应用，并确定这些公式中的系数，可以设计一个简支的小梁，并在梁的跨中作用循环集中荷载的作用。由于梁的跨度较大，可略去剪力的影响，在跨中截面可简单视为只受弯矩的作用。根据疲劳实验循环荷载作用N次后测得的跨中挠度wm(N)，求得梁跨中底缘处的应变εm(N)为

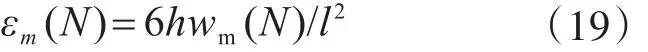
式中：h为梁高；l为梁的跨度。

这样可以根据疲劳实验测得的跨中挠度随荷载循环次数的变化规律，得到梁底缘应变εm(N)与循环荷载重复作用次数N的关系曲线。由式（17）可得到λn与循环荷载重复作用次数N的关系曲线，利用可得到梁由于损伤而产生的中性轴偏移量y0与循环荷载重复作用次数N的关系曲线，也可得到梁的有效惯性矩与循环荷载重复作用次数N的关系曲线。利用εm(N)与循环荷载重复作用次数N的关系曲线取关系曲线中稳定段的斜率。从而应用式（18）可预测矩形截面梁疲劳寿命Nf。

3 纯弯曲梁疲劳脆性开裂实例分析

用AC16型沥青混合料成型50 mm×50 mm×240 mm的小梁试件（弹性模量E=1 800 MPa，强度极限σ=1.2 MPa），在MTS810材料试验系统上进行三点加载的应力控制疲劳试验（加载F=0.2 kN，频率f=10 Hz，半正矢波，温度T=15℃）。记录循环加载次数N分别为0、1 500、3 000、4 500、6 000、7 500时的小梁底缘的挠度，并将实验结果记录在表1中。

表1 小梁疲劳损伤实验结果Table 1 Small beam’s fatigue damage measured by experiment

由表1的记录的实验结果，应用最小二乘法进行曲线拟合得到小梁跨中挠度wm随荷载循环次数N变化的关系曲线，可取关系曲线中稳定段的斜率记录在表2中。首先，选定指数p=4.0［11］，对于不同的Dm，由式（16b）可求得相应的λn；然后，利用式（18）可求得相应的荷载循环次数N；最后，利用利用式（17）得到相应的梁跨中底缘的挠度wm，并将上面理论计算的结果记录在表2中。这样，可样理论上可以得到小梁跨中挠度随荷载循环次数变化的关系曲线。从图2中理论计算结果和实验结果比较可以看出，理论解与实验解比较接近。

表2 小梁疲劳损伤的发展规律Table 2 The law of fatigue damage rule of small beam

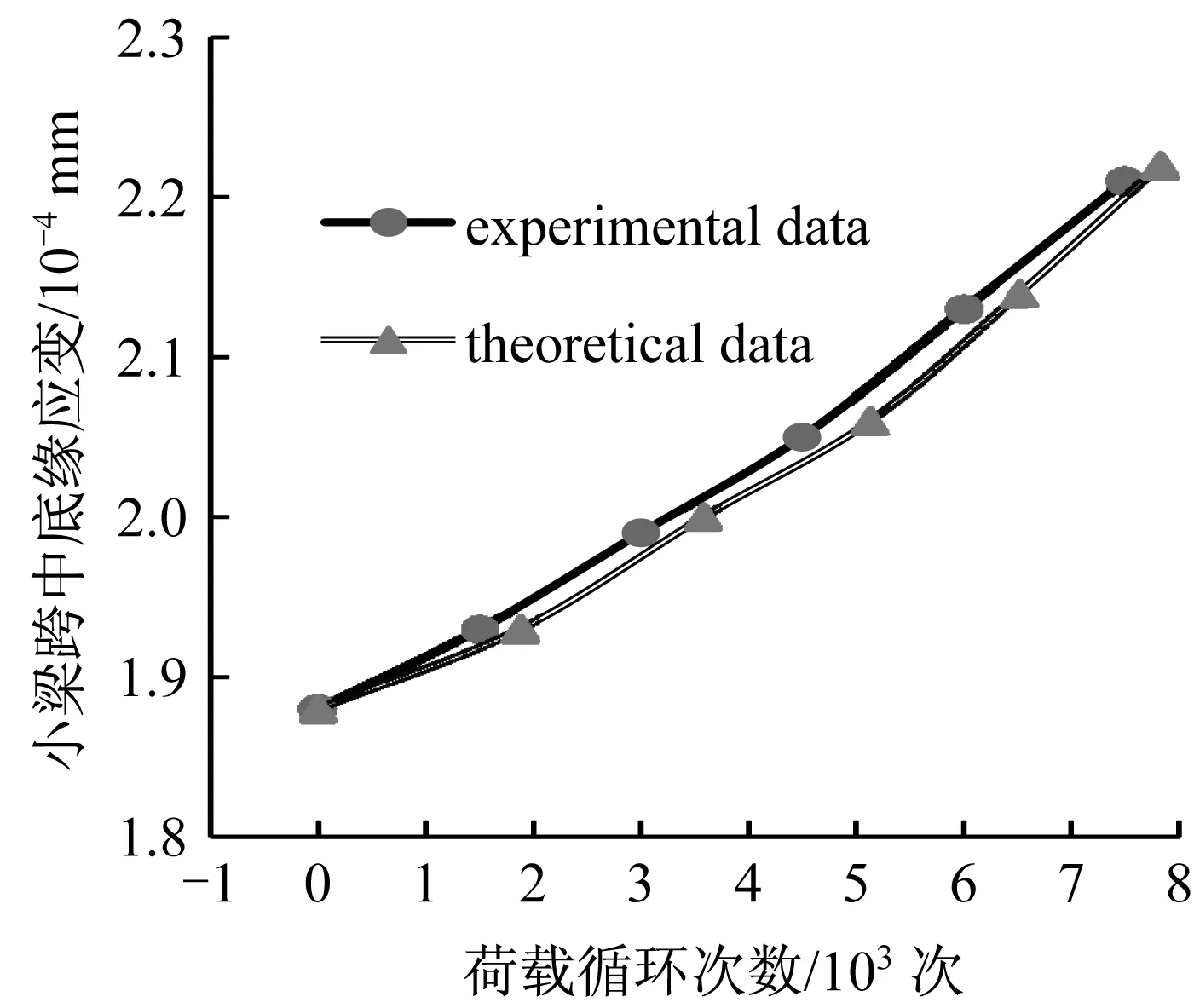
图2 梁跨中底缘应变与荷载循环次数关系曲线Fig.2 Relationship between beam midspan strain at the botom and number of load cycles

图3 给出了小梁跨中底缘的损伤随荷载循环次数的变化关系曲线。从图中可以看出，跨中底缘损伤随着荷载循环次数的增加而增大，当跨中底缘损伤达到0.5时，荷载循环次数达到7 827次，试验结果的疲劳寿命为7 787次，也比较接近。图4给出了中性轴偏移量y0随荷载循环次数变化的曲线，从图中可以看出，偏移量y0随着荷载循环次数的增加而增大。图5给出了有效惯性矩-I随荷载循环次数变化的曲线，从图中可以看出，有效惯性矩随着荷载循环次数的增加而减小。

图3 梁跨中底缘损伤与荷载循环次数的关系曲线Fig.3 Relationship curve between the damage of midspan at the bottom and number of load cycles

图4 中性轴偏移量与荷载循环次数关系Fig.4 Relationship curve between neutral axis offset and the number of load cycles

图5 有效惯性矩和荷载循环次数关系曲线Fig.5 Relationship curve between effective moment of inertia and the number of load cycles

4 结 论

应用损伤力学的理论分析梁的弯曲疲劳损伤的演化并预测其疲劳寿命，通过理论分析和实验结果的比较，说明本文提出的梁的纯弯曲损伤模型应用方便而结果比较可靠。通过实验得到的小梁跨中挠度随荷载循环次数变化规律与理论计算的结果吻合，说明本文提出的梁疲劳损伤模型是合理的。图2-图4均表明随着荷载循环次数的增加，梁内的疲劳损伤在不断地累积和发展，最后发生疲劳破坏。