基于Pasternak双参数模型的滑坡段埋地管道受力分析方法

(中国地质大学(武汉)工程学院，湖北武汉，430074)

近年来，长输管道工程迅猛发展，已成为能源输送的重要手段之一，其中很大一部分管道需要穿越地质环境复杂、滑坡灾害频发的地段，严重威胁着管道的安全运营。对处于滑坡作用下的埋地管道，目前常用有限单元法或基于Winkler模型的弹性地基梁法进行分析计算。近年来，有限单元法在研究管土接触问题中得到了广泛应用。譬如在滑坡段埋地管道应力应变分布随参数变化规律研究[1-2]、滑坡作用下埋地管道强度失效分析[3]、滑坡段管道内力变形分析[4-7]、埋地管道的安全下埋深度及多跨管段间相互作用研究[8-9]等方面都有广泛的应用；朱勇等[10]采用有限元分析与模型试验相结合的方法对滑坡作用下管道受力变形进行了研究。虽然有限单元法适应性强，能够处理复杂问题，但因其使用较为复杂，在对实际工程问题的分析上尚有一定困难。基于Winkler模型的弹性地基梁法则假定土体是由离散弹簧组成的弹性体，地基反力与埋地管道上任一点的位移成正比，将管道看成小变形的半无限长梁，研究了管道的应力及变形特性[11-14]。与有限单元法相比较，基于Winkler模型的弹性地基梁法概念比较明确，求解简单，实用性更高，但该方法没有考虑土弹簧间的相互作用，在具有少许黏性或具有传力性土介质中应用误差较大。Winkler模型在描述实际土体的连续性态中的固有缺陷及弹性连续介质模型在数学上的复杂性加速了双参数弹性模型的发展，其主要沿着2个方向进行。第一种是从弹性连续介质模型开始并引入约束或简化位移分布与应力的某些假设，Vlasov模型是其中的典型代表，但其土模型公式是以变分法的应用为基础的，在求解中涉及到参数迭代，计算过程较为复杂[15-17]。第二种是由不连续的Winkler模型产生的并在各个弹簧之间提供力学的相互作用以消除其不连续的性态，Pasternak模型是其中的典型代表，其采用2个参数来综合反映土体特征，假设土弹簧单元与一层只能产生剪切变形而不可压缩的竖向单元相连接，考虑了土弹簧间传力作用，反映了土体变形连续性，更符合土体的受力变形特性，由此得到了广泛的应用[17-18]。张望喜等[19]以能量变分法原理为基础研究了地基反力模量为常数的水平受荷桩解答，提高了计算精度；魏东旭等[20]采用考虑剪力的双参数模型，获得了双参数地基推力长桩的有限差分解，提高了推力桩的设计计算水平；梁发云等[21]采用改进的地基反力模量，提出了一种可考虑剪切作用的水平受荷桩的简化分析方法，可明显提高水平受荷桩的计算精度。综上所述，Pasternak双参数模型运用于水平受荷桩的分析计算中，提高了水平受荷桩的设计水平与计算精度。而在滑坡作用下埋地管道受力变形的计算中多采用基于Winkler模型的弹性地基梁法，在具有少许黏性或具有传力性土介质中应用误差较大。鉴于此，本文作者基于Pasternak模型，提出一种考虑轴向载荷的滑坡段埋地管道受力分析方法，讨论轴向载荷、地基反力系数及地基剪切刚度对滑坡段埋地管道受力变形性状的影响，该方法比基于Winkler模型的弹性地基梁法具有更高的计算精度。

1 滑坡作用下埋地管道力学模型

在滑坡作用下，埋地管道受滑坡体推力作用会发生变形，其力学模型可以简化成Pasternak弹性地基上的连续梁模型(图1)。图1所示平面为管道在滑坡作用下发生变形的平面。图1中：q为滑坡体对管道的作用力，N/m；l为滑坡体宽度，m。为了简便计算，做出如下假设：

1)假设下滑土体对埋地管道的压力q沿滑坡宽度l均匀分布[22]，且不计下部土体对管道的支撑作用(最危险工况)；

2)在滑坡作用下，下滑土体对管道的压力是导致管道变形的主要作用力，管道自身及管内介质重力作用对管道变形影响较小，故忽略其重力作用对管道变形的影响；

3)假设管道沿轴向刚度均匀，不考虑管与管连接处的端效应，将其看成整体；

4)假设管道变形和受力关于截面C对称。

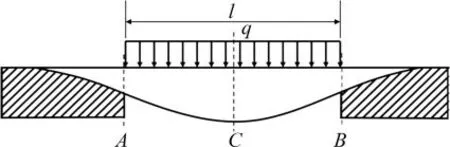
图1 滑坡作用下管道力学模型Fig.1 Mechanical model of pipeline under landslide

1.1 Pasternak双参数地基模型

Pasternak双参数弹性模型是在Winkler弹性模型的基础上假设各弹簧单元间存在着剪切的相互作用。这种相互作用是通过将弹簧单元与一层只能产生横向剪切变形而不可压缩的竖向单元相连接(图2)实现的[18]。在二维情况下，模型可以用下式表示：

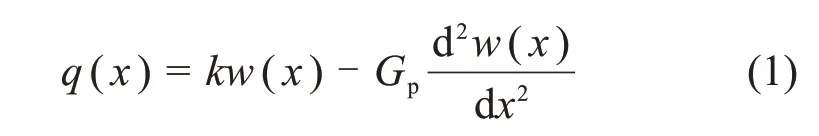
式中：q(x)为地基的反力，kN/m2；k为地基反力系数，kN/m3；w(x)为埋地管道挠度，m；Gp为地基剪切刚度，kN/m。

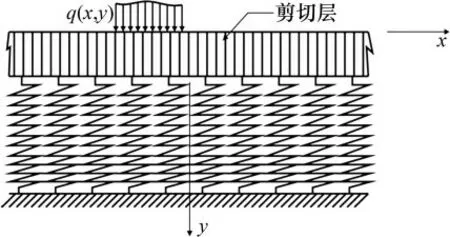
图2 Pasternak双参数地基模型Fig.2 Pasternak double-parameter foundation model

当式(1)中Gp=0时，该模型即退化为Winkler模型。

1.2 Pasternak双参数弹性模型常数的确定

描述双参数模型的常数k和Gp，可采用下列方法得出[17]。

方法一：常数k和Gp可由现场试验测定(例如载荷板试验)。

方法二：可认为常数k和Gp与土介质的弹性常数(例如土体弹性模量Es、土体泊松比υs、孔隙比e等)有关，可由试验室确定。

方法三：可将常数k和Gp与土介质弹性常数Es和υs关联起来，并根据土与基础相互作用问题的解类比而得。

TERZAGHI等[23-25]对用荷载板试验测定地基反力系数k进行了详细评述。研究表明从荷载板试验测定k受板的尺寸、形状、埋置深度等因素影响，k并不是土介质的固有性质。在确定Gp时，不仅需要量测荷载板的沉降量，还需要量测出临近荷载板处土表面的挠度。由于双参数土基础的界面挠度局限于非常临近的加载面，一般的常规荷载板试验难于量测，导致误差较大。因此，一般不建议采用这种方法确定Gp。

方法三将模型常数与土介质弹性常数Es和υs关联起来，根据土与基础相互作用问题的解类比得到常数取值，与方法一和二相比不需进行繁杂试验，且精度符合工程需求。因此，本文采用方法三确定模型常数。方法三可将双参数地基模型的常数与弹性常数Es和υs加以联系。其中VLAZOV等[15]提出的经验公式比较具有代表性，如下式所示：

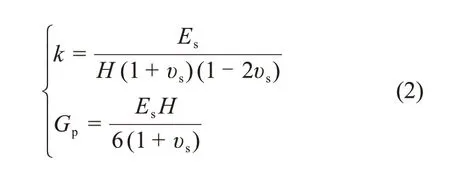
式中：Es为地基土的弹性模量，kPa；υs为地基土的泊松比；H为弹性层厚度，m。

YAO等[26]通过数值模拟技术对受水平荷载作用影响的桩侧土范围进行了研究，认为其受影响范围为11d(d为桩的直径)。因此，近似地将该范围作为地基土的弹性层厚度，即H=11D(D为埋地管道的外径)，实际上H的取值与土性质有关。

2 挠度和内力分析

将图1所示的埋地管道分成2部分进行分析，滑坡体外管道和滑坡段管道。

2.1 滑坡体外管道分析

建立图3所示力学模型，X轴为未发生滑坡时的管道轴线，Y轴为滑坡周界的左侧边界。ω0为滑坡周界处管道挠度，m；M0为滑坡周界处管道弯矩，N·m；θ0为滑坡周界处管道转角，rad；S0为管道轴力，N。滑坡段管道对滑坡体外管道作用以剪力0.5ql、弯矩M0及轴力S0代替(滑坡周界处管道转角很小，可近似认为轴力S0平行于X轴)。由于轴力S0主要影响管道轴向变形，因此忽略轴力对管道横向变形的影响，将滑坡体外管道看成是Pasternak弹性地基上的半无限长梁。

为了计算方便，统一规定：弯矩以管道上侧纤维受拉为正；管道轴力以拉力为正。

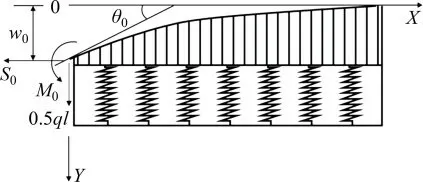
图3 滑坡体外管道力学模型Fig.3 Mechanical model of landslide external pipeline

将埋地钢管看成梁，其挠度Y与荷载q、地基压力p之间的关系为

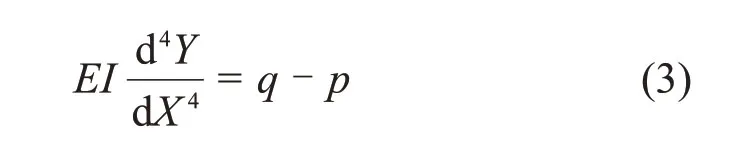
式中：E为钢材的弹性模量，Pa；I为管道的截面惯性矩，m4。

根据Pasternak弹性地基模型，式(3)可写成

式中：D为管道的外径，m。

滑坡段管道对滑坡体外管道的作用是其变形的主要原因，因此荷载q可以近似忽略。代入式(4)可得

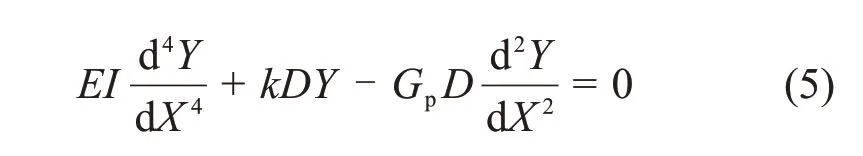
式(5)的通解为

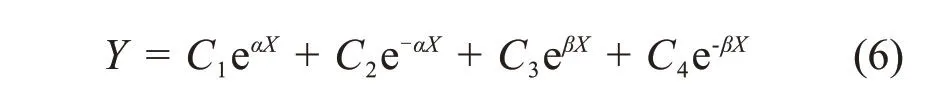
由定性分析可知，当X→∞时，Y→0可知C1=C3=0，因此式(6)变为

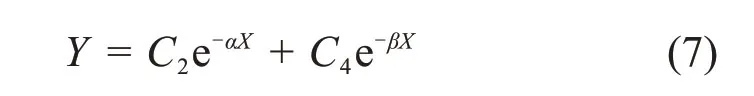
由式(7)可得管道任意截面转角θ、弯矩M及剪力Q的表达式：

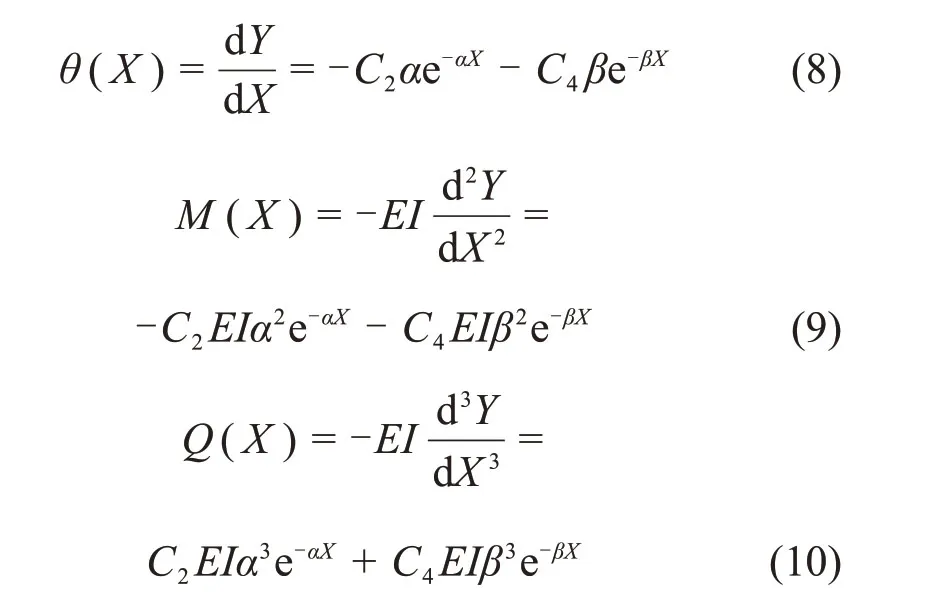
原点处的边界条件为

由此解得

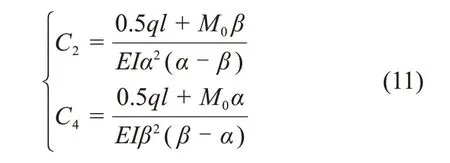
挠度ω0和转角θ0为

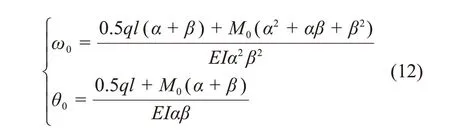
2.2 滑坡段管道分析

建立图4所示力学模型，x轴为未发生滑坡时的管道轴线，y轴为滑坡周界的左侧边界。滑坡体外管道滑坡段管道的作用力以剪力0.5ql、弯矩M0及轴力S0代替。

图4 滑坡段管道力学模型Fig.4 Mechanical model of landslide section pipeline

对滑坡段l，管道弯曲的微分方程为

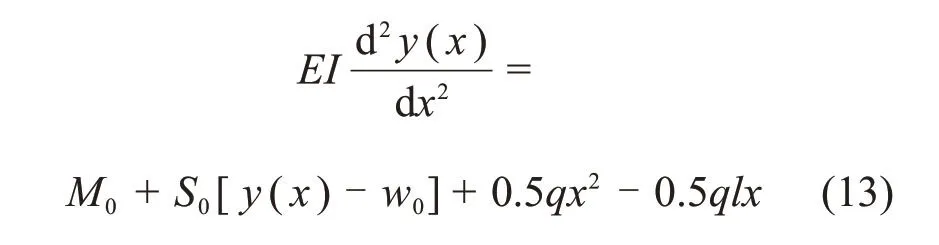
方程的解为

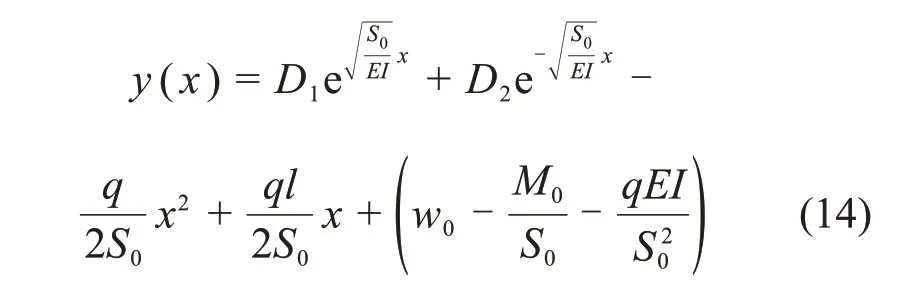
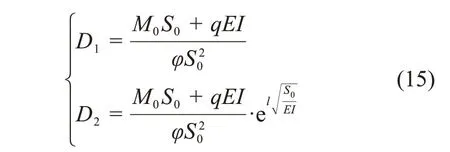
滑坡周界x=0处管道转角为

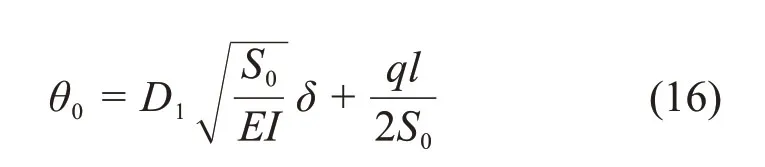
根据变形协调性，滑坡体内、外管道在交界处挠度和转角相等。从以上分析可知，挠度相等条件已经满足。至于转角相等条件，由式(12)与式(16)可知

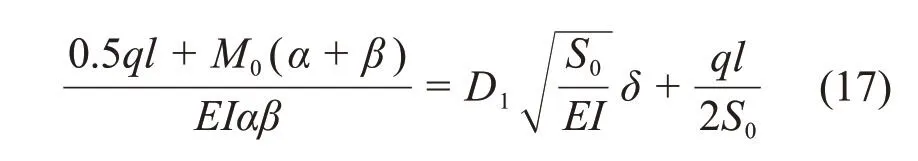
由式(17)可得M0为

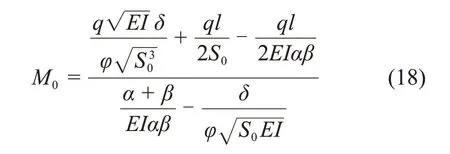
由式(14)可得滑坡段管道任意截面转角θ和弯矩M的表达式为：

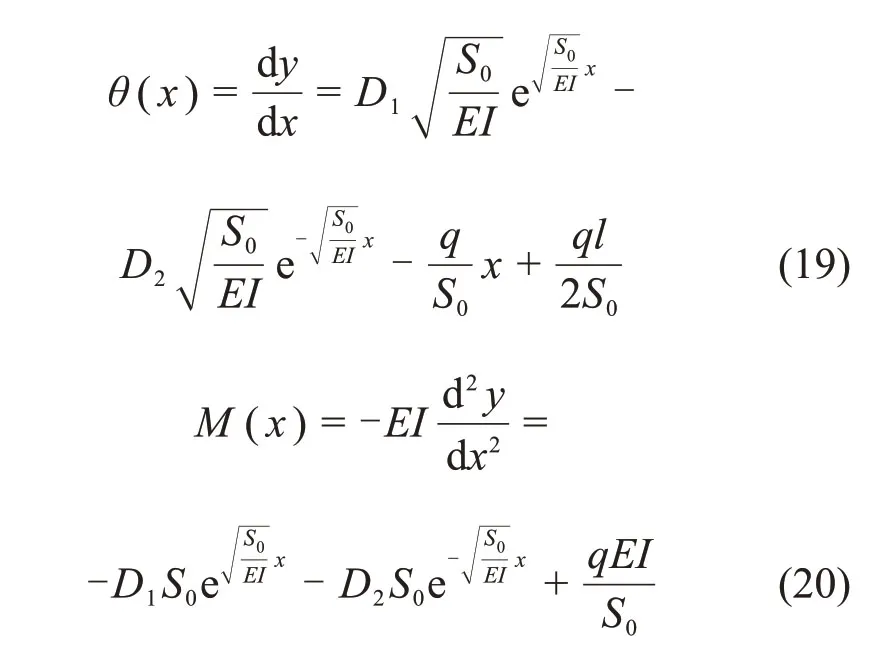
由式(14)可得管道在x=l/2处中点挠度f为

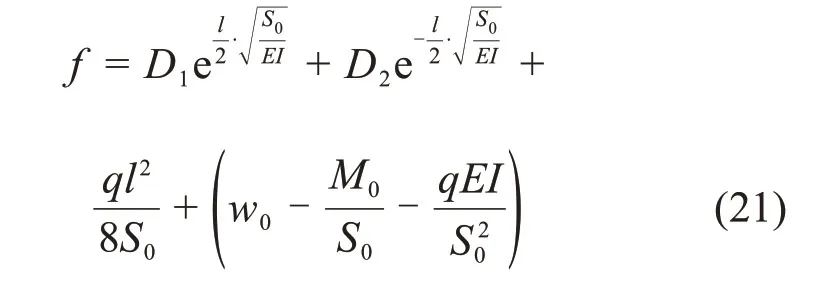
2.3 纵向位移计算

为了求解上述模型中的未知参量S0，补充管道纵向位移的关系式。

以滑坡体内管道为研究对象，根据管道轴向应变的几何非线性关系可得

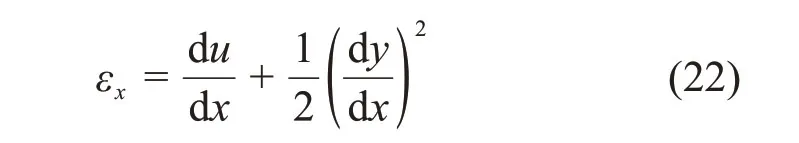
式中：εx为管道轴向应变；u为管道轴向位移，m。

根据材料力学胡克定律，管道轴向应变表达式为

式中：A为管道的截面积，m2。

联立式(22)和式(23)可得

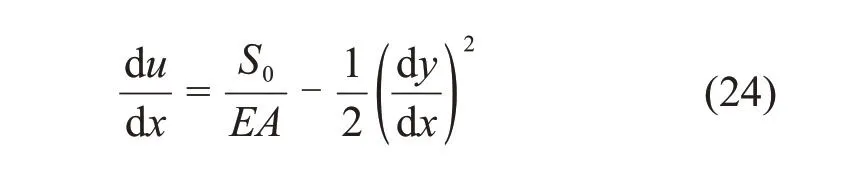
为了方便计算，滑坡体内挠曲线近似取为y=由式(24)可得

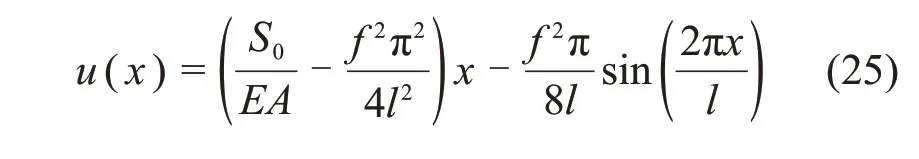
由截面C的轴向位移为0，可得

联立式(21)和式(26)可解得S0。

3 管道强度校核

由于管道是薄壁，一般情况下可以忽略径向应力，因此，管道的应力状态可以简化为环向应力和轴向应力的双轴应力状态[12]。

管道轴向应力σx及环向应力σθ的计算公式为：

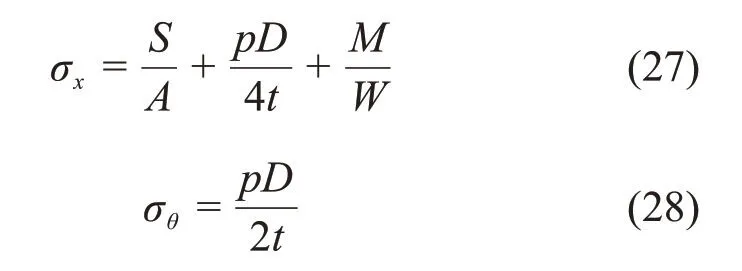
式中：S为管道轴力，N；M为管道弯矩，N·m；W为管道截面抗弯模量，m3；p为管道输送压力，Pa；t为管道的壁厚，m。

根据强度理论，可对上述应力状态进行组合，判别管道的可靠性。Mises屈服准则为常用的强度理论。

Mises屈服准则也被称为最大形状改变比能条件，其应力表达式为

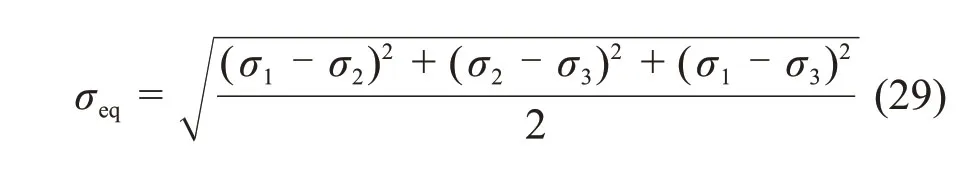
对于管道，多属平面问题，σ3=0，因此式(29)可简化为

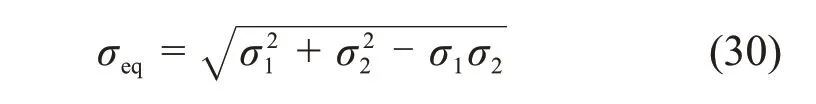
式中：σeq为当量应力，Pa；σ1，σ2和σ3分别为第一、第二和第三主应力，Pa。

4 算例分析及结果讨论

根据上述算法，使用MATLAB计算软件，编写了管道受力、变形计算程序，并以忠武输气管道沿线小担子垭滑坡[12]为例，对管道受力、变形特性进行了分析。

斜坡地层为志留系龙马溪组黄绿色页岩，表层覆盖残坡积碎块石土，滑体厚度为2～4m，平均宽度l=40m，管道从滑坡体中下部通过。滑坡体变形模量E0=0.035GPa，泊松比υs=0.35，滑坡体对管道的作用力q=4.35 kN/m。

管道材料为X65型钢，弹性模量E=207GPa，最低屈服极限σs=450MPa。管道规格为Φ711mm×7.9mm，即外径D=711mm，壁厚t=7.9mm，管道输送压力p=4.0MPa。

由于模型参数受多种因素影响，针对不同工况和土体情况划分不同参数取值较为困难。因此，本文针对特定的工况对参数进行取值，并以此为标准选取较大值、较小值研究各参数对管道受力变形的影响作用。为研究轴向载荷、地基反力系数及地基剪切刚度对管道变形和受力的影响，分别对考虑轴向载荷和不考虑轴向载荷、不同地基反力系数及不同地基剪切刚度条件下管道受力变形进行计算。

4.1 轴向载荷

为了研究轴向载荷对管道变形和受力的影响，分别计算Pasternak地基模型和Winkler地基模型管道在考虑轴向载荷和不考虑轴向载荷作用下的挠度、弯矩和Mises应力。计算结果见图5(由于管道变形对称，因此取管道长度l/2进行计算)。

由图5(a)可知：考虑轴向载荷作用时，2种地基模型计算的挠度都要小于不考虑轴向载荷时的计算结果，说明轴向载荷对减小管道变形有利，在设计计算时应给予考虑。由于双参数弹性模型弥补了Winkler模型在描述实际土体连续性态中所固有的缺陷，因此考虑轴向载荷的Pasternak模型具有更高的计算精度。

由图5(b)～(c)可知：考虑轴向载荷作用时，2种地基模型计算所得弯矩要小于不计轴向载荷时的计算结果，管道Mises应力大于不计轴向载荷时的计算结果。截面A与截面C弯矩及Mises应力取极值，应该作为管道强度设计和校核的控制点，并将其作为研究重点。

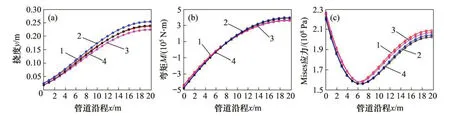
图5 管道挠度、弯矩及Mises应力与管道沿程的关系Fig.5 Relationship between pipeline deflection,bending moment,Mises stress and pipeline

轴向载荷并没有改变管道受力、变形的变化规律，但对计算结果产生了显著影响，在管道强度的设计和校核中是不可忽略的，因此下述各节计算中均考虑轴向载荷。

4.2 地基反力系数

计算不同地基反力系数管道挠度、弯矩及Mises应力。计算结果见图6。

由图6可知：管道挠度、截面C上的弯矩与Mises应力随地基反力系数的增加呈下降趋势，而截面A上的弯矩与Mises应力呈上升趋势。地基反力系数的增加，加强对管道截面A上的约束，增大弯矩载荷，提高Mises应力水平；土体对管道截面A上约束的加强，减小截面C上的弯矩，降低Mises应力水平。

当地基反力系数较大时，Pasternak地基模型与Winkler地基模型的计算结果相近(图6)。因为地基反力系数较大时，荷载对临近单元体的传力作用减弱，管道受力变形性状主要受地基反力系数影响，Pasternak模型近似退化为Winkler模型。

4.3 地基剪切刚度

计算不同地基剪切刚度管道挠度、弯矩及Mises应力，计算结果见图7。

由图7可知：管道挠度、截面C上的弯矩及Mises应力随地基剪切刚度增加呈上升趋势，而截面A上的弯矩及Mises应力呈下降趋势。地基剪切刚度的增加，加强土弹簧间的传力性能，减弱土体对管道截面A上的约束，减小截面A的弯矩载荷，降低Mises应力水平；土体对管道截面A上约束的减弱，增加截面C上的弯矩，提高Mises应力水平。

地基剪切刚度较大时，荷载对临近单元体的传力作用较大，减弱土体对管道的约束作用，地基剪切刚度对管道受力变形性状有较大影响，这也是基于Winkler模型的弹性地基梁法误差较大的原因。

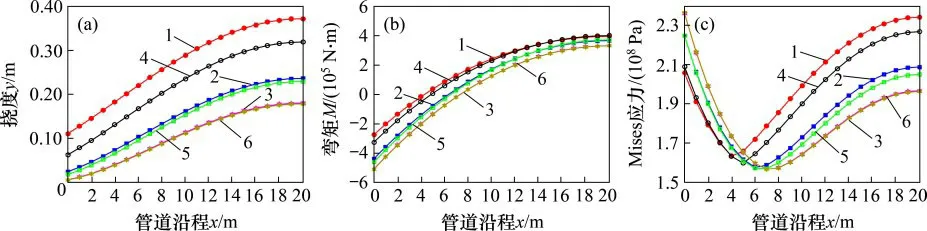
图6 不同地基反力系数时管道挠度、弯矩及Mises应力与管道沿程关系Fig.6 Relationship between pipe deflection,moment and Mises stress and pipeline under different coefficient of subgrade reaction

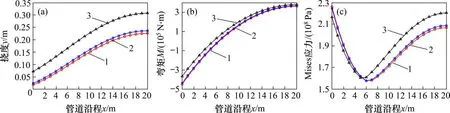
图7 不同地基剪切刚度时管道挠度、弯矩及Mises应力与管道沿程关系Fig.7 Relationship between pipe deflection,moment and Mises stress and pipeline under different shear stiffness of foundation

5 结论

1)基于Pasternak模型的滑坡段管道受力分析方法弥补了基于Winkler模型的弹性地基梁法的固有缺陷，能够考虑荷载对临近单元体的传力性，具有更高的计算精度。

2)轴向载荷对减小管道变形有利，对滑坡段管道受力影响显著，在埋地管道强度设计和校核中不能忽略。

3)地基反力系数较大时，荷载对临近单元体的传力作用减弱，管道受力变形性状主要受地基反力系数影响，Pasternak模型近似退化为Winkler模型，2种模型计算结果相近。

4)地基剪切刚度较大时，荷载对临近单元体的传力作用较大，减弱了土体对管道的约束作用，对管道受力变形性状有较大影响。