Ease-Off修形准双曲面齿轮减振优化设计
2020-06-17蒋进科刘钊彭先龙
蒋进科 刘钊 彭先龙
(1长安大学 汽车学院 汽车运输安全保障技术交通行业重点实验室,陕西 西安710064;2.西安科技大学 机械工程学院,陕西 西安710054)
准双曲面齿轮广泛应用于车辆主减速器,随着螺旋锥齿轮向高速、重载方向的发展,强度和振动噪声已成为影响产品质量的瓶颈。螺旋锥齿轮齿面复杂,其动力学的研究在模态分析[1]、振动稳定性[2-3]及动态响应等方面取得了一些成果。动力学模型主要考虑误差、时变啮合刚度、侧隙、摩擦力等因素影响,且动力学模型的建立主要以参考点受力分析为基础,包括纯扭转模型[4]、弯-扭-轴耦合模型[5]、弯-扭-轴-摆耦合模型[6-7]。文献[8-9]中基于多体动力学理论与迟滞接触动力学方法,提出考虑全齿面动态接触关系的螺旋锥齿轮三维接触动力学模型和动力学分析方法。文献[10]中结合齿面接触分析(TCA)和齿面承载接触分析(LTCA)方法获得啮合位置几何参数及刚度,表明弧齿锥齿轮的高阶较2阶传动误差齿面的多转速动态啮合力下降更为明显,实际上还是因为高阶传动误差齿面适配量较小即重合度大。以上研究为螺旋锥齿轮动力学的理论研究和工程应用做出了贡献,然而由于齿面几何复杂,关于螺旋锥齿轮的减振降噪技术研究尚鲜见。
齿面修形是降低齿轮传动系统的振动和噪声的有效途径,广泛应用于圆柱齿轮,从动力学和静力学已有深入的研究。静力学主要以承载传动误差幅值(ALTE)最小为优化目标[11],动力学主要以啮合线振动加速度均方根最小为优化目标[12],静态性能最优时的修形参数未必使得系统的动态性能最优[13]。文献[14]中主要考虑修形改变了轮齿接触间隙进而改变了啮合刚度激励,或者把刚度视为常量,主要考虑修形改变轮齿传动误差产生啮合线位移激励,通过与有限元法修形对比,表明刚度激励模型更为准确。可见,动力学齿面修形设计的关键是正确地描述修形参数对系统的啮合刚度和啮合误差等激励的影响。文献[15]中建立切片法修形斜齿轮刚度模型,文献[16]中建立考虑实际运动状态的修形直齿轮刚度模型,并研究修形参数对系统振动响应的影响规律,其刚度计算方法仅适用于齿面几何简单的圆柱齿轮及其齿廓修形情况。文献[17]中基于有限元法获得修形直齿轮啮合刚度及静态传递误差,并引入到动力学分析模型中,衡量齿轮修形优劣。有限元法需要精确的齿面模型且计算耗时,在工程应用中难以推广。准双曲面齿轮采用局部共轭原理加工,已经体现了轮齿修形的概念,局部综合法[18]和高阶传动误差齿面研究[19]等有效地解决了齿面边缘应力集中问题,但造成了齿轮副失配量过大,导致了振动噪声的增加。为了控制齿面修形量,相对共轭齿面的修形方法即齿面Ease-off修形方法,已成为螺旋锥齿轮齿面设计与加工的研究热点[20],但主要集中于以ALTE最小进行Ease-off修形齿面设计[21],Ease-off修形齿面加工参数的反求[22-24],Ease-off修形齿面的TCA仿真及有限元软件LTCA仿真验证[25-27]。由于Ease-off修形准双曲面齿轮几何的复杂性,使齿面综合误差、啮合刚度等参数的确定十分困难,螺旋锥齿轮动力学减振修形优化设计鲜见。
为了进一步提高汽车驱动桥品质,基于齿间间隙和齿面法向间隙产生原理,进行小轮Ease-off修形齿面设计;结合TCA、LTCA方法[28],准确获得轮齿综合啮合刚度,以啮合位置受力分析为基础,建立准双曲面齿轮弯-扭-轴耦合8自由度集中质量动力学模型;以法向振动加速度均方根最小为目标,通过优化确定最佳Ease-off修形齿面,并讨论了修形导致的刚度波形及幅值变化对系统动态特性的影响。
1 小轮Ease-off修形齿面表达
按照齿轮啮合理论和安装关系,将大轮齿面视为假想齿轮刀具与小轮工件按照名义传动比对滚,获得与大轮完全共轭的小轮齿面。Ease-off修形齿面改变了共轭齿面的齿间间隙和齿面法向间隙,齿间间隙如图1(a)所示;齿面法向间隙如图1(b)所示,可通过图1(c)的齿廓修形曲线经旋转变换映射得到,设计思路详见文献[29]。图1中ε0~ε4及λ1~λ2为齿间接触间隙参数,d1、d2、q1、q2及θa为齿面法向接触间隙参数。
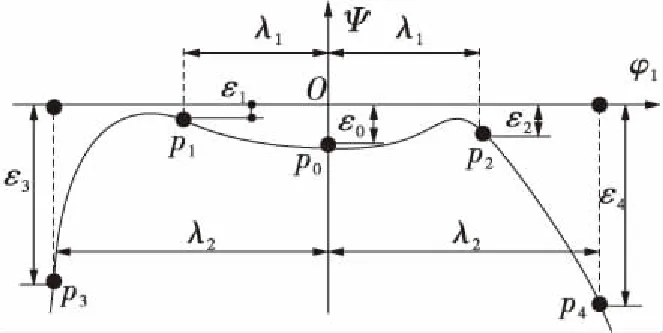
(a)四阶传动误差曲线
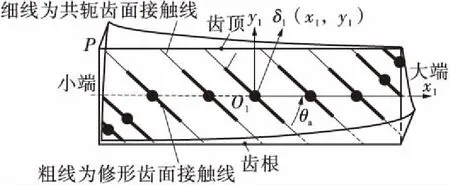
(b)接触线修形示意

(c)接触线修形曲线
在仅包含传动误差的小轮齿面上,叠加齿面法向间隙δ1,得到修形小轮的解析齿面,其Ease-off曲面表达式为
δ(u,β)=(R1γ(u,β)-R10(u,β))·N10(u,β)
(1)
(2)
式中:R10、N10为与大轮完全共轭的小轮齿面位矢、法矢;R1、N1为仅包含传动误差的小轮齿面位矢、法矢;R1γ、N1γ为小轮Ease-off修形齿面位矢、法矢;δ为Ease-off修形量;u、β为小轮理论齿面参数。
2 振动优化模型
通过TCA、LTCA方法得到一个啮合周期轮齿法向位移,将法向位移转化为啮合线转角即被动轮承载传动误差(单位为s)
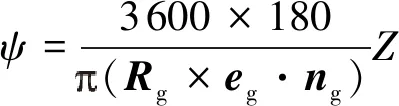
(3)
式中:Rg、ng、eg分别为被动轮接触点位矢、单位法矢、轴线方向单位矢量;Z为法向承载变形。
采用集中质量法,建立考虑时变刚度的螺旋锥齿轮系统沿x轴、y轴、z轴的横向弯曲振动、轴向振动及法向扭转振动即弯-扭-轴耦合8自由度动力学模型如图2所示,其广义位移可表示为{xp,yp,zp,θp,xg,yg,zg,θg},动力学方程为
(4)
式中:xi,yi,zi(i=p,g)为齿轮中心点沿坐标轴3个方向的平移振动位移;下标“p”代表主动齿轮,“g”代表被动齿轮,以下同;θi(i=p,g)为齿轮中心点绕着坐标轴的扭转振动角位移;mi、Ii、Ti(i=p,g)为齿轮质量、转动惯量及扭矩;ci j、ki j(i=p,g,j=x,y,z)为齿轮各方向的支撑阻尼、支撑刚度;nij(i=p,g,j=x,y,z)为啮合点法矢;rl(l=p,g)为啮合点旋转半径;Fn为法向啮合力。啮合点旋转半径表示为
rl=Rl×el·nl
(5)
(nl=[nlxnlynlz],l=p,g)
式中:Rl、nl、el(l=p,g)为齿轮接触点位矢、单位法矢、轴线方向单位矢量。
修形改变轮齿啮合刚度、啮合线误差,LTCA方法求解的啮合刚度已包含了齿形误差、安装误差的影响,因此不需要再次考虑,主要考虑轴频误差激励,法向动态啮合力为
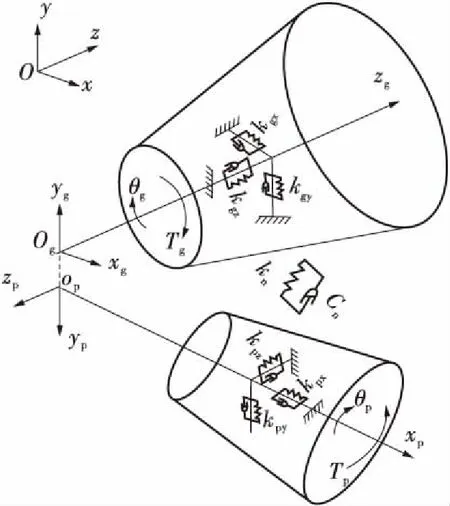
图2 准双曲面齿轮副集中质量振动模型
Fig.2 Vibration model based on lumped mass for hypoid gears
(6)
式中:Fsn为静态法向啮合力;Kn、Cn为轮齿的综合啮合刚度、啮合阻尼;en为轴频误差,A、ω、φ0为综合轴频误差幅值、角速度及初始相位。主、被动轮的扭转位移可通过啮合点法线的相对位移统一起来,因此上述方程组中引入相对位移sn作为新的自由度,从而将两个扭转振动位移消去,使得系统的自由度数降为7个。将所求的一个啮合周期的啮合刚度通过傅里叶级数拟合,带入动力方程;通过量纲统一化,利用变步长四阶 Runge-Kutta数值积分方法对其求解。以法向振动加速度均方根最小为优化目标,目标函数表示为
G(y)=min{a/a0}
(7)
式中:y为优化变量即齿间间隙参数(ε1~ε4及λ1、λ2)和接触线法向间隙参数(d1、d2、q1、q2及θa);a0、a为共轭齿面、理论齿面的法向振动加速度均方根。优化过程即改变齿面初始间隙求解TCA、LTCA、动力学方程的一个非线性迭代过程,目标函数与设计变量间为隐式关系,且存在多个局部解,因此,传统的优化算法不适合所研究的问题,而粒子群算法具有全局收敛性,可以求解具有多个局部极值的非线性优化问题,只需要构造包含TCA、LTCA、系统动力学方程计算结果的适应度函数即可,具体的优化算法不再赘述。
3 算例与分析
对于高精度齿轮副,为了增加受载后的实际重合度,主要考虑接触路径大倾斜设计。以一对弧齿准双曲面齿轮的工作面为例,基本参数见表1。大轮额定扭矩为1 000 N·m,小轮输入转速5 000 r/min,最大轴频误差为A=3 μm;优化的最优Ease-off曲面参数见表2。为了研究修形后承载变形的幅值(刚度的幅值)与振动的关系,表3中列出优化迭代过程中不同修形齿面的ALTE、法向振动加速度与共轭齿面对应数值之比(优化力度)。最优Ease-off齿面ALTE降低到65%,法向振动降低到15%,而优化Ease-off齿面1的ALTE基本没变,法向振动却降低到22%;可见ALTE最小时,振动未必最小,法向振动不仅与承载变形的幅值有关,还与承载变形曲线的形状有关。
最优Ease-off齿面TCA仿真如图3(a)所示,在啮入、啮出端有一定修形量,接近内对角接触;

表1 准双曲面齿轮副基本参数

表2 最优Ease-off修形参数
表3 修形齿面的传动误差幅值及法向振动与共轭齿面比值
Table 3 The ALTE and normal vibration of modification tooth to conjugate tooth ratio

不同修形齿面承载传动误差幅值 / %啮合线振动加速度 / %最优Ease-off齿面6515理论齿面105126优化Ease-off齿面110622优化Ease-off齿面24996优化Ease-off齿面35633
理论齿面TCA仿真如图3(c)所示,其为内对角接触,在啮合转换点有一定的幅值,可以降低安装误差的敏感性,齿面适配量较大;二者的Ease-off曲面如图3(b)、(d)所示,分别与接触区域匹配一致,传动误差越大,对应的齿面修形量也较大。

(a)最优Ease-off齿面TCA仿真(b)最优Ease-off齿面修形量
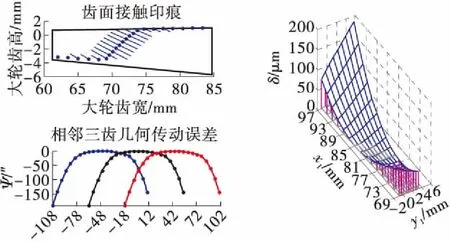
(c)理论齿面TCA仿真 (d)理论齿面Ease-off修形量
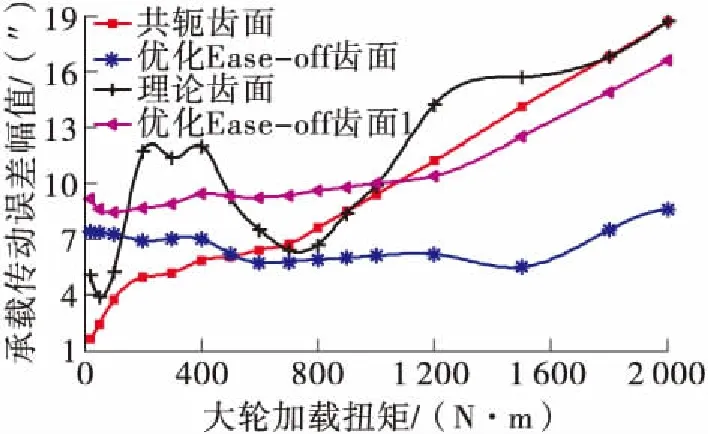
(e)多载荷承载传动误差幅值
这里一个啮合周期分成8等份,TCA接触点为22,理论重合度略大于(22-1)/8=2.6。多载荷ALTE如图3(e)所示,共轭齿面实际重合度不变,随载荷增加ALTE不断增加;理论齿面适配量过大、椭圆长轴设计过小时,随载荷增加,实际重合度增加程度不同,因此ALTE出现多个极值;最优Ease-off齿面适配量较小、椭圆长轴设计较大时,随载荷增加,重合度呈现增加,直至不变,因此载荷≥1 400 N·m时ALTE逐渐增加。
在法向自由度方向上,理论齿面修形量过大导致齿轮副啮合刚度最小,相对振动位移最大,共轭齿面反之;最优Ease-off齿面振动速度最为平稳,且为单周期简谐振动规律,见图4(a)。最优Ease-off齿面振动加速度均方根减小到共轭齿面的15%,主要为啮合频率(666.67 Hz)及3倍频,修形主要减小了3倍啮合频率的振动幅值,可见系统的某阶固有频率接近2000 Hz,见图4(b)。同样,最优Ease-off齿面的法向动态啮合力在理论静态啮合力附近变化且振幅最小,对啮合力的变化部分进行傅里叶变换,主要为啮合频率及2倍、3倍频,见图4(c)。
为了研究振动与刚度的关系,表3中不同修形齿面的啮合刚度及频谱如图5所示:共轭齿面的平均啮合刚度最大,而理论齿面修形量最大,平均啮合刚度最小。对刚度曲线的波动部分做傅里叶变换表明:①共轭齿面啮合频率幅值及3倍频幅值均较大,优化Ease-off齿面2的3倍频幅值略小于基频幅值;②理论齿面、最优Ease-off齿面、优化Ease-off齿面1、优化Ease-off齿面3的基频幅值大于谐波成分幅值且谐波成分幅值很小。
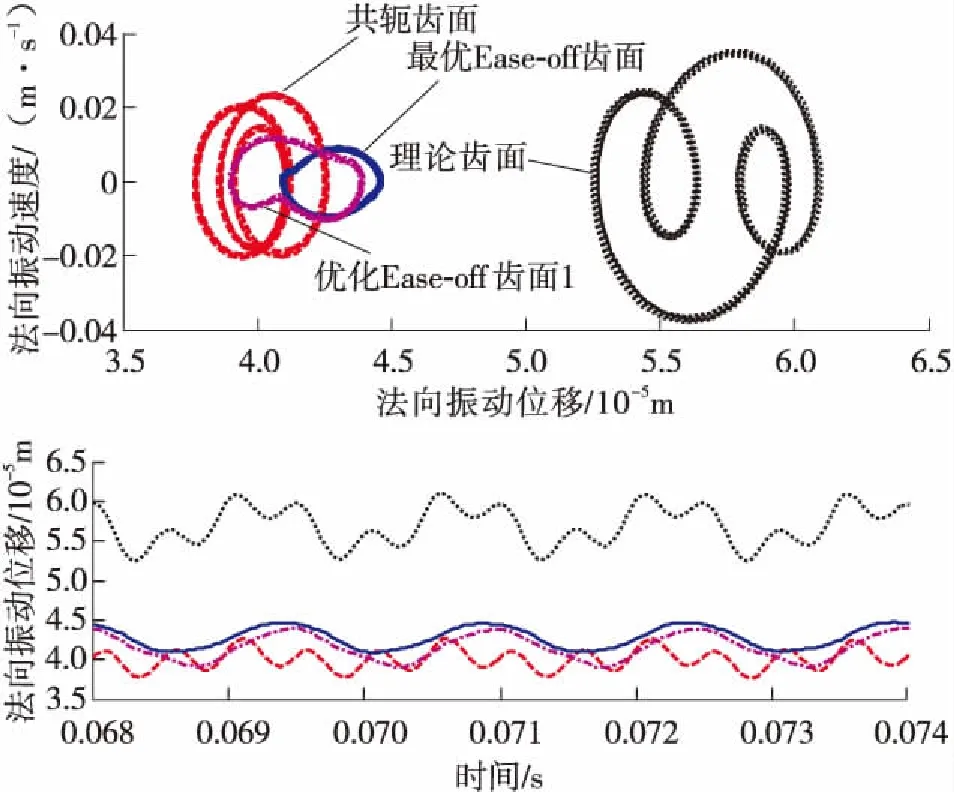
(a)法向振动位移与相图
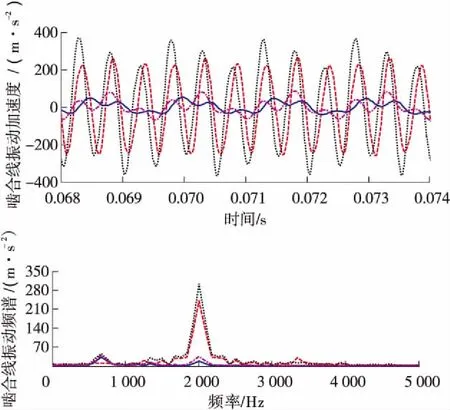
(b)法向振动加速度与频谱

(c)法向啮合力与频谱
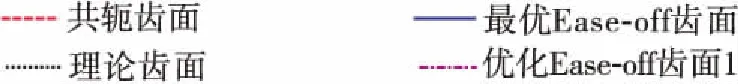
图4 额定工况准双曲面齿轮系统动态响应
Fig.4 Dynamic response of rated condition for hypoid gears
结合表3振动优化力度可以看出:①额定工况下理论齿面ALTE基本无变化(105%),由于修形量过大,平均啮合刚度下降过多且刚度曲线主要为啮合频率,其振动有所增加(126%);②优化Ease-off齿面1的ALTE也基本无变化(106%),平均啮合刚度下降较少且刚度曲线中主要为啮合频率,而振动降低到22%;③优化Ease-off齿面2的ALTE下降到49%,平均啮合刚度下降较少,且刚度曲线中主要为啮合频率及其3倍频,而振动加速度变化不大(96%);④最优Ease-off齿面的ALTE下降到65%,平均啮合刚度下降较少且刚度曲线主要为啮合频率,而振动加速度降低到15%;
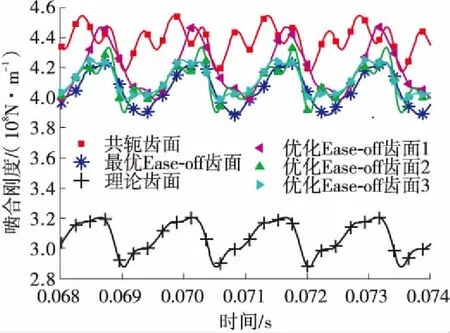
(a)齿面啮合刚度

(b)齿面啮合刚度频谱
⑤优化Ease-off齿面3的ALTE下降到56%,平均啮合刚度下降较少且刚度曲线主要为啮合频率,振动加速度降低到33%。综上所述,当修形量过大时导致刚度下降较多引起法向振动增加;修形后平均啮合刚度下降较少且刚度曲线振幅降低及谐波幅值很小时法向振动明显降低,而刚度曲线中的谐波成分较大时法向振动增加;平均啮合刚度相差不大情况下,刚度曲线的形状较幅值对振动的影响更为敏感。
共轭齿面在3 200、5 600 r/min处出现共振,动态啮合力增加;理论齿面修形量过大,尽管在5 600 r/min的啮合力减小,但是在8 000 r/min后仍有较大共振,啮合力增加;最优Ease-off齿面、优化Ease-off齿面1的法向啮合力在整个转速范围内明显降低,见图6(a)。同样,共轭齿面在3 200、5 600 r/min处出现共振,法向振动加速度明显增加;理论齿面的共振转速略有降低且在5 600 r/min附近振动减小;最优Ease-off齿面与优化Ease-off齿面1在共振转速附近振动明显降低,但在4 500 r/min附近振动增加,见图6(b)。随载荷增加共轭齿面振动逐渐增加;理论齿面随载荷增加振动产生波动,特别是载荷较小时实际重合度较小,因此振动较大;最优Ease-off齿面与优化Ease-off齿面1随载荷增加,振动增加较为缓慢,而相对于共轭齿面和理论齿面整体降低;多载荷ALTE曲线基本可以反映振动随载荷的变化趋势,见图6(c)。
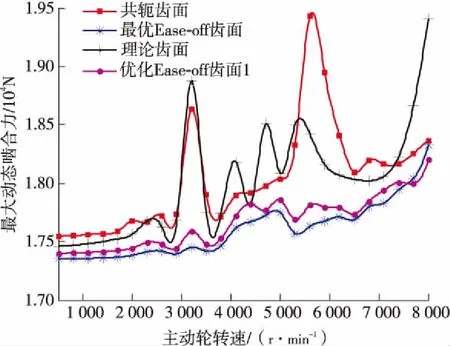
(a)多转速法向啮合力(额定扭矩为1 000 N·m)

(b)多转速法向相对振动加速度均方根(额定扭矩为1 000 N·m)
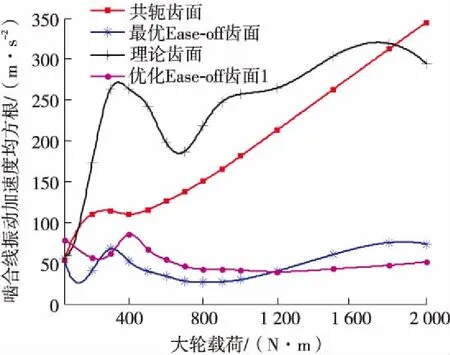
(c)多载荷法向相对振动加速度均方根(小轮转速5 000 r/min)
Fig.6 Dynamic response for hypoid gear with multi-load and multi-speed
4 结论
为了提高汽车驱动桥综合传动性能,提出Ease-off修形准双曲面齿轮齿面减振设计方法。
(1)基于齿间间隙和齿面法向间隙产生原理,对HFT法的小轮齿面进行拓扑Ease-off曲面设计,并叠加于共轭齿面表达修形齿面;
(2)结合TCA、LTCA方法,获得轮齿综合啮合刚度,以一个啮合位置受力分析为基础,应用集中质量法建立弧齿锥齿轮弯-扭-轴耦合的8 自由度动力学型;以法向振动加速度均方根最小为目标,通过优化确定最佳Ease-off修形齿面,并讨论了修形导致的刚度波形及幅值变化对系统动态特性的影响;
(3)当修形量过大时导致刚度下降较多引起法向振动增加;修形后平均啮合刚度下降较少且刚度曲线振幅降低及谐波幅值很小时法向振动明显降低,而刚度曲线中的谐波成分较大时法向振动增加;平均啮合刚度相差不大情况下,刚度曲线的形状较幅值对振动的影响更为敏感;
(4)通过优化ALTE最小减小振动的方法未必可以降低振动,ALTE降低后也易导致刚度曲线(传动误差曲线)中的高频成分增加,产生新的振动;多载荷ALTE基本可以反映振动随载荷的变化趋势。
