基于RBF神经网络的气动人工肌肉PID位置控制
2020-06-17刘凯陈伊宁吴阳王扬威
刘凯 陈伊宁 吴阳 王扬威
(1.南京航空航天大学 机电学院,江苏 南京 210016;2.东北林业大学 机电工程学院,黑龙江 哈尔滨 150040)
气动人工肌肉(PMA)是随着机器人技术发展而产生的新型气动驱动器,与传统的液压、电机驱动相比具有结构简单、功率/质量比高、柔顺性好等特点,可用于驱动仿生机器人[1]、康复机器人[2]、多自由度平台[3-4]等。目前PMA建模方法主要可以分为静态建模和动态建模,常通过增加摩擦力项、添加与PMA运动方向相反的偏移力等方法来优化数学模型[3],利用该数学模型与传统PID形成复合控制可以获得良好的控制效果[5]。但由于PMA属于时变、非线性系统,外负载、温度变化等会导致传统PID无法获得满意的动态控制效果。多数文献中采用自适应鲁棒控制、滑模控制、人工神经网络控制等[6-8]来提高控制性能。2011年,王建等[9]将模糊控制器加入普通PID 控制器中,用于控制一种外骨骼可穿戴式上肢康复机器人。2012年,沈伟等[10]设计了一种自适应模糊小脑模型神经网络控制器,解决了初期动态跟踪误差较大的问题。同年,王冬青等[11]用三层递归神经网络(RNN)建立模型。2013 年,焦磊涛[12]利用双层 PID控制器对一种基于PMA的仿蛙腿跳跃机器人进行精确位置控制。Kumar等[13]设计了一种基于RBF网络的混合控制器,对冗余机器人末端位置进行有效跟踪。
在控制系统中结合RBF网络能够在线辨识系统的未建模部分。文中将设计基于RBF网络的PID控制器,实现PMA精确快速的动态位置跟踪控制,凭借RBF的快速学习能力,根据外负载大小自适应调整PID参数。
1 PMA数学模型建立
1.1 PMA结构分析
试验室选用的PMA是由德国FESTO公司研制的气动肌腱(如图1所示),该PMA内部橡胶管充气后轴向弹性变形,外围编织网限制橡胶管只能径向变形,因此充气后直径变粗,长度缩短,产生收缩力,对负载产生驱动作用。

图1 FESTO气动肌腱
PMA特性分析中首先需要建立负载拉力F、收缩率ε和充入气压P三者之间的数学模型。如图2所示,b和n分别为编织套纤维的长度和根数,δ为纤维与轴线的夹角,σ0为PVC软管及纤维之间的初始截面厚度,σ为瞬时截面厚度,D0为纤维外层初始外径,D为瞬时外径,S为截面积。单根纤维在充放气过程中长度保持不变,PMA实时长度L会发生改变。
(1)
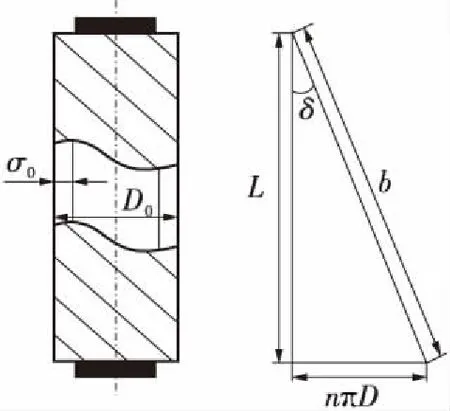
图2 PMA结构简图
1.2 PMA数学模型
气动人工肌肉静态测试原理如图3所示,测试平台如图4所示。测试台主要由气动人工肌肉、比例伺服阀(SMC 公司,ITV1050-312-L2)、气泵(V-0.25/ 12.5)、气压传感器(SMC 公司,PSE530)、位移传感器(GRFRAN公司,PK-M-400)、8通道数据采集卡(ART公司,PCI8735)、8通道运动控制卡(ART公司,PCI8201)、拉力传感器(PSK-100)和测控软件组成。比例阀可与电压信号成比例地对气压进行无极控制,灵敏度高,电压值0~10 V线性对应气压值0~0.9 MPa;控制卡和采集卡插在PC机的PCI插槽中,减压阀保证气压稳定,不会过大导致损坏比例阀和人工肌肉。
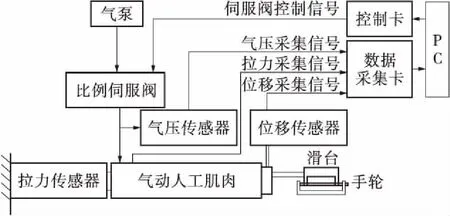
图3 PMA静态测试原理图

图4 PMA静态测试平台
采用如上测试台进行单根PMA静态测试试验,气压范围0.1~0.8 MPa,每间隔0.1 MPa输入气压,每组重复2到3次,试验取平均值,得到如图5所示110 mm PMA特性曲线。通过Matlab曲线拟合工具箱拟合曲线(图5)得到的数学模型简单实用,可直接应用于PMA位置控制试验。为了体现PMA的刚度特性,并提高模型的实用性,利用多次试验数据对已有模型[14]进行改进。定义名义刚度系数kc(p),因负载是导致肌肉长度和截面积变化的原因,可将其认为是PMA刚度变化的间接因素,通过量纲分析法来建立kc(p)与截面积S、收缩力F的经验公式:
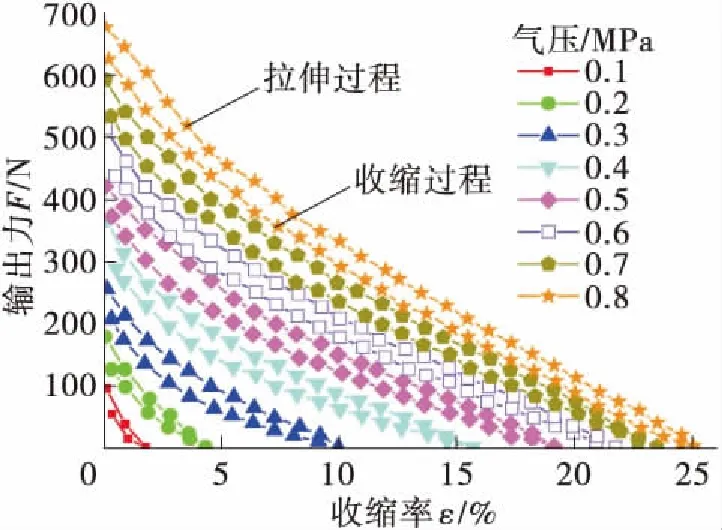
图5 110 mm PMA特性曲线
(2)
将图5中的试验数据带入式(2)可以得到名义刚度系数特性曲线,同样用Matlab曲线拟合工具箱拟合特性曲线:
kc(p)=a(p)ε2+b(p)ε+c(p)
(3)
式(3)的拟合结果如表1所示。

表1 拟合结果
联立式(2)、(3)可得到数学模型。
2 PMA位置控制
2.1 基于RBF网络的PID控制
PID控制具有非常成熟的理论基础,由于其算法简单、鲁棒性好和可靠性高等,得到众多学者的青睐。在PMA实际位置控制中,PID参数在一定的外负载范围内都能实现很好的位置控制,但当外负载超过这个范围后控制系统会出现不稳定的情况,需要重新选择PID参数。因此,将RBF网络引入PID控制器是利用其非线性变换能力来在线辨识PMA外负载所在范围。
RBF网络是一种局部逼近前馈式神经网络,其基本结构如图6所示[15]。令RBF网络输入层数为n,输入向量为X=[x1,…,xn]T,隐含层节点数为m,选取径向基函数为高斯径向基函数H=[h1,…,hm]T:
(4)
式中,bj为径向基函数的节点基宽参数,Cj为第j个节点的中心向量,且Cj=[cj1,…,cji,…,cjn]T。假设隐含层到输出层的权向量为w=[w1,…,wm]T,第k次迭代时RBF网络输出为qm(k):
qm(k)=h1w1+…+hjwj+…+hmwm
(5)
考虑到外负载、气源气压和系统摩擦等因素对PMA数学模型的影响,结合RBF网络对系统未建模部分的快速学习能力,设计了基于RBF网络的PID控制策略,以实现PMA精确的位置控制,其结构框图如图7所示,其中,理论气压输入Pd是由外力F外和收缩率通过PMA数学模型计算所得,u是基于RBF网络的PID控制的补偿项。

图6 RBF网络结构
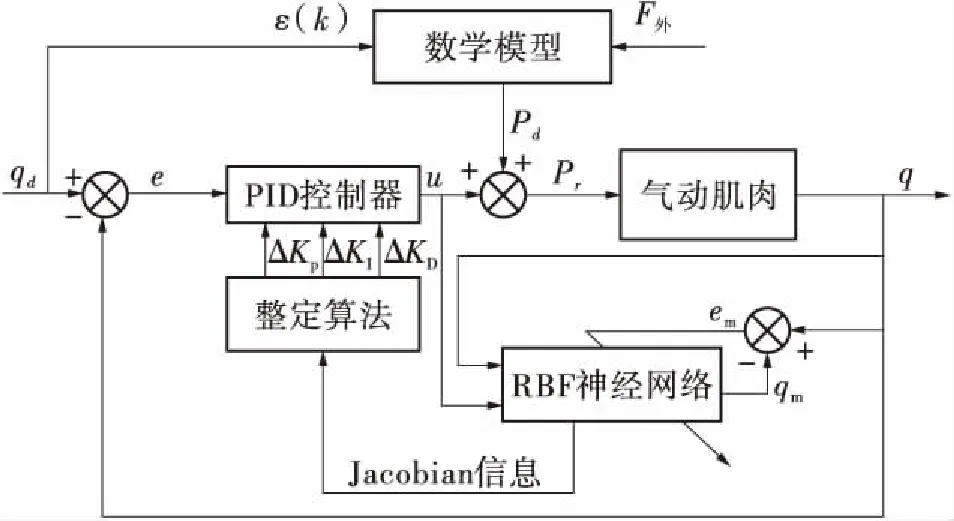
图7 RBF网络PID控制结构框图
Fig.7 Structure block diagram of PID control based on RBF network
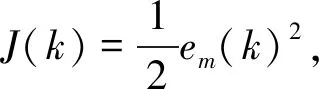
(6)
PID控制器输入xc及输出u为:
(7)
同样采用梯度下降法求取增量式PID参数调整量ΔKP、ΔKI和ΔKD:
(8)
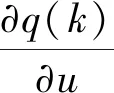
(9)
试验开始前,需要确定的参数有:RBF网络的结构、权值向量、中心向量及节点基宽向量的取值范围,学习速率η和ηc、动量因子ζ的取值等。
2.2 试验结果与分析
类似于静态测试平台,PMA动态测试平台是为了模拟PMA在收缩或拉伸过程中的位置控制,需另外加上活动的砝码来提供额定外负载,如图8所示。

图8 PMA动态测试平台
分别采用传统PID控制策略和基于RBF网络的PID控制策略,进行PMA阶跃位置控制试验,以外负载F=100 N、阶跃信号S=10 mm为例,在收缩充气过程中,基于RBF网络的PID控制相较于传统PID控制时超调量下降了76.5%,调节时间下降了47.8%,稳态误差下降了60%[14]。
从多组不同负载下PMA位置控制试验结果可看出,传统PID控制只能在一定的负载范围内实现较好的位置控制,当负载发生变化时,原有的PID参数就不再合适。基于RBF网络的PID控制能根据外负载的变化情况自适应调整PID参数,比传统PID控制的响应速度快,调节时间短,超调量小。
为了进一步突显基于RBF网络的PID控制策略效果,取幅值、周期不规则变化的正弦波为跟踪信号,进行动态位置控制试验,得到与传统PID控制的控制对比效果如图9所示,对应误差如图10所示。
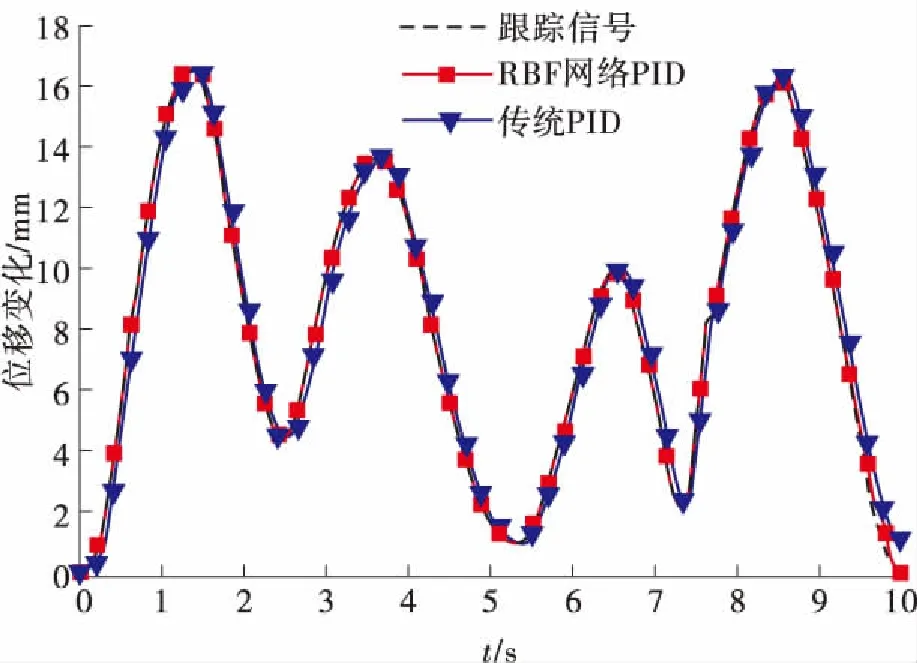
图9 110 mm PMA控制结果对比
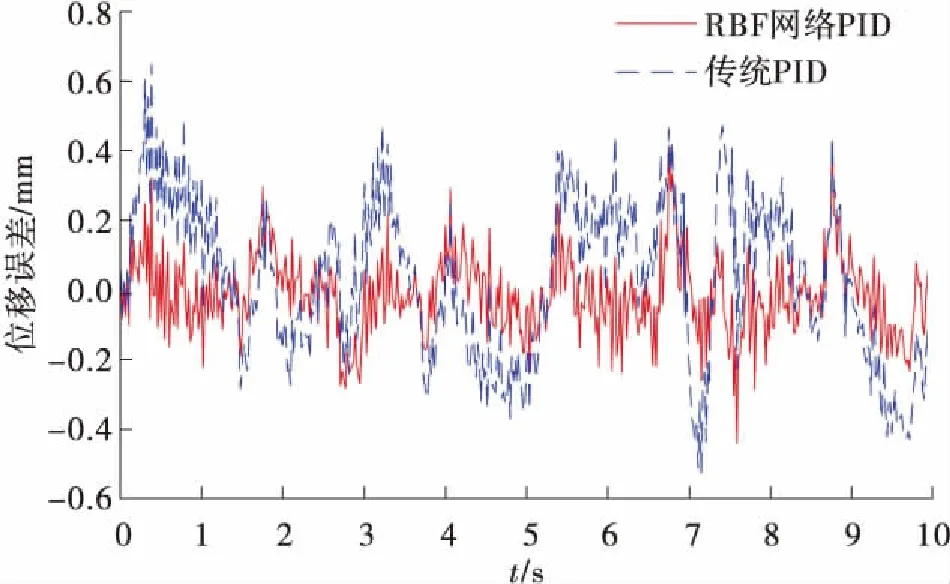
图10 110 mm PMA控制误差对比
同时给出了动态控制过程中的外负载曲线,如图11所示。给定砝码为150 N,动态试验过程中受惯性力影响,肌肉外负载呈现规则变化趋势。在控制过程中(如图9所示),传统PID得到的位移曲线相对于跟踪信号有一定滞后现象,结合图10可以看出误差在跟踪信号的波峰波谷阶段偏大,最大误差为0.624 mm,平均误差为0.37 mm。基于RBF网络的PID控制效果明显得到改善,最大误差为0.411 mm,平均误差为0.18 mm。
在以上110 mm PMA位置控制试验中,基于RBF网络的PID动态控制误差在0.5 mm以内,平均误差在0.2 mm以内,分别比传统PID减少了30%及50%,可知该控制器受外负载的变化影响比传统PID控制小,适应能力更强。为了验证该控制策略的普遍性,对另一种规格的PMA(FESTO公司,DMSP-10-55-RM-CM)进行了上述建模分析及RBF网络参数辨识,该PMA长度为55 mm,最大收缩率为25%,同样取跟踪信号为幅值、周期不规则变化的正弦波,给定砝码150 N,得到动态位置控制曲线及误差如图12、图13所示。在55 mm规格PMA的动态位置控制试验中,基于RBF网络的PID动态控制误差为0.233 mm,平均误差为0.12 mm,分别比传统PID减少了41%及48%,能更好地补偿数学模型误差,适应外负载变化的情况,从而更好的实现PMA精确的动态位置控制。
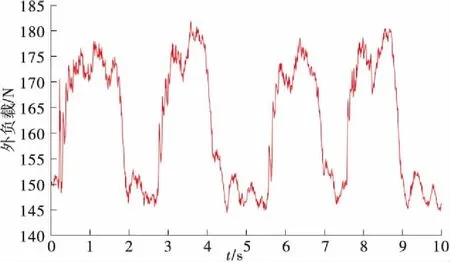
图11 110 mm PMA外负载曲线
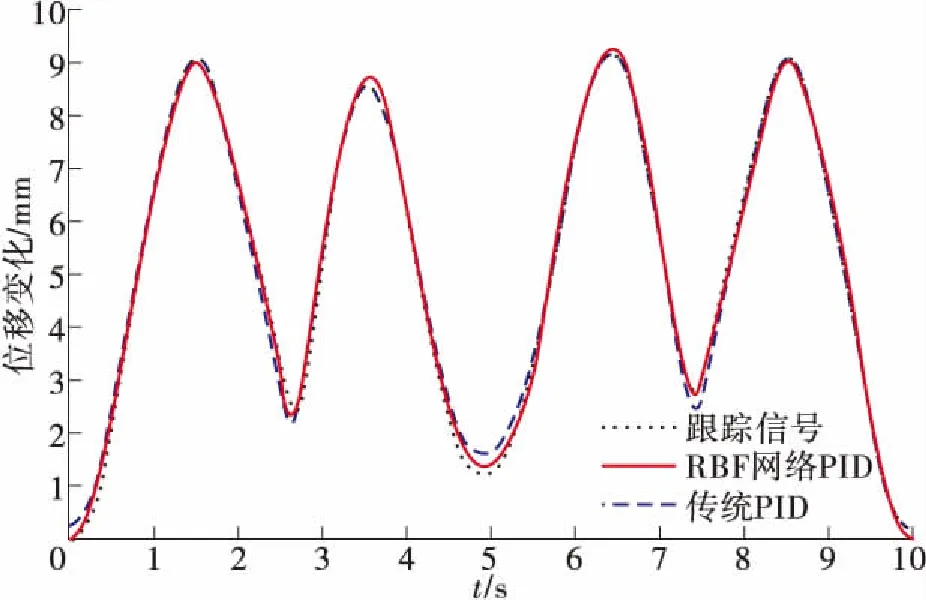
图12 55 mm PMA控制结果对比

图13 55 mm PMA控制误差对比
3 结语
基于PMA特性分析研究了其驱动原理,搭建了PMA静态测试平台,在0.1~0.8 MPa气压范围下对PMA的输出力和收缩率进行了多次测量试验。根据理论模型和测试数据,改进了直接拟合静态特性曲线的方法,利用Matlab拟合名义刚度系数,建立了新的PMA数学模型,模型求解精度较好,验证了模型应用的可行性。
考虑外负载、气源气压和系统摩擦等因素对PMA数学模型的影响,结合RBF网络对系统未建模部分的快速学习能力,设计了一种基于RBF网络的PID控制策略,以实现PMA精确的位置控制。搭建了PMA动态测试平台,并对两种规格的PMA进行了多组位置控制试验。从多组试验结果可以看出,传统PID控制只能在一定的外负载范围内实现较好的位置控制,而基于RBF网络的PID控制能根据外负载的大小自适应调整PID参数,以适应不同的外负载变化情况,比传统PID控制的响应速度快,调节时间短,超调量小,能更好地补偿其数学模型误差和实现其位置控制的精确控制。
后续研究将使用已研究完成的两种PMA驱动一种三自由度并联平台,利用文中的改进模型及控制器实现轨迹跟踪控制。
