基于残差学习的多阶段图像压缩感知神经网络
2020-06-17杨春玲裴翰奇
杨春玲 裴翰奇
(华南理工大学 电子与信息学院,广东 广州 510640)
奈奎斯特-香农采样定理中指出:为了无失真的恢复原始信号,采样信号的频率不能低于原始信号的两倍带宽。2006年,Donoho等[1-3]提出的压缩感知理论(CS)证明了当原始信号具备稀疏特性时,采样频率可以远低于奈奎斯特定理的要求。在压缩感知中,采样和压缩的过程同步完成,有效解决了传统采样中先采样后压缩的策略所造成的资源浪费。凭借以上优势,压缩感知理论在学术界和工业界引起了广泛的关注和研究。
在图像压缩感知中,随机观测矩阵由于符合等距性限制条件(RIP)[2],且具有较好的重构效果,被广泛应用在图像的采样中。同时,分块压缩感知理论(BCS)[4-5]因其在存储与计算方面的优势而被广泛用于图像压缩感知中。在这个框架下,图像被分成多个不重叠的图像块单独采样与重构,以减小整体的计算量。但是,不容忽视的一点是,分块压缩感知框架引起了不良的块效应:在恢复图像中,由于不同分块之间相对独立的观测与重建,在各个块之间出现了大量不连续的边界。块效应降低了重构图像的视觉质量,特别是在低采样率下,这个问题尤为严重。
图像压缩感知中的另外一个核心问题是图像的重构算法,这部分在很大程度上决定了最终恢复结果的优劣。基于图像的结构特性,文献[5]中提出的平滑投影Landweber算法(SPL)将自然图像的恢复结果提升到了一个较高的水平;通过利用不同图像块之间的的相似信息,基于组稀疏表示的重构算法(GSR)[6]获得了目前最好的图像重构性能,并且对图像中的噪声有着一定的抑制效果。但是,由于需要大量的迭代,这些恢复算法都有着高耗时的缺点,使得图像压缩感知难以实际应用。
最近,基于卷积神经网络的图像压缩感知框架的出现,为图像压缩感知的研究和应用带来了新的思路。
2012年,文献[7]中提出的AlexNet展现出了卷积神经网络(CNN)的性能潜力,并引起了一次新的研究热潮。过去的几年中,深度学习(DL)领域的研究得到了进一步的发展,在多种高阶语义下的计算机视觉任务中取得了大量的研究成果,如对象检测、多目标跟踪和动作识别等。同时,基于卷积神经网络的低阶语义计算机视觉任务的研究也引起了关注,例如在图像超分辨率重建(SR)[8-12]与图像去雾算法(Image Dehazing)[13]等病态逆问题的研究中,深度学习均取得了不错的结果,展现出其性能的优越。
近年出现的一些基于深度学习的图像压缩感知(ICS)算法的研究,表现出了深度学习强大的学习能力和极快的运行速度。Kulkarni等[14]首次提出基于卷积神经网络的图像压缩感知重构算法,取得了不错的重构效果。文献[15]中提出在重构神经网络中引入Resnet的结构,从而在图像压缩感知的恢复过程中学习更加丰富的图像特征。Zhang等[16]设计了一种新颖的网络结构,能够较好的模仿传统图像压缩感知中的迭代收缩重构算法。受到基于稀疏表示的图像压缩感知重构算法启发,文献[17]中ConvCSNet尝试将稀疏性嵌入神经网络的设计之中。文献[18]中提出一种基于深度学习的多尺度残差网络结构来学习图像中的多尺度信息,增强了重构算法对噪声的鲁棒性。文献[19]中提出一种端到端的神经网络结构,成功复现了传统图像压缩感知中的经典重构算法——平滑投影Landweber算法。基于文献[19]的工作,Cui等[20]提出了压缩感知观测矩阵的神经网络学习方法,弥补了传统观测矩阵设计过程中的不足。总的来说,与传统图像压缩感知相比,基于神经网络的压缩感知方法显著地降低了重构算法的时间成本,但仍未解决重构图像中的块效应问题,并且重构端网络结构缺乏针对性,限制了最终的重构性能。
为了解决上述问题,文中提出了一种针对图像压缩感知的全新神经网络结构——MSResICS:在采样端,放弃了传统的分块线性映射采样框架,与之对应的是一个基于残差学习的全卷积图像采样子网络,相比之下,该子网络结构不仅避免了分块压缩感知带来的块效应,而且成功地在采样部分引入非线性的特征提取方法,保留了更加丰富的图像信息;在恢复端,首先引入一个基于插值卷积的初始重构子网络,从采样值中整合特征并恢复初始重构图像,其次为了进一步提升重构图像的效果,在前两个子网络的基础上,加入多阶段图像增强子网络,以生成多幅残差图像,对恢复结果做进一步的细化;最后通过实验仿真来分析MSResICS的具体性能。
1 图像压缩感知基本原理
在图像压缩感知中,有两个主要问题:1)图像的高效采样;2)图像的高质量重构。在经典的分块压缩感知中,观测值由观测矩阵的线性映射得到:
yb=Φbxb
(1)
式中,xb为N×1维的原始图像块列矢量,yb为M×1维的分块采样信号,Φb为M×N维的随机观测矩阵。在压缩感知中,由于M≪N,从采样信号yb中重构原始信号xb是一项病态逆问题。但压缩感知原理指出,如果目标信号xb在变换域Ψ是稀疏的,可以通过求解以下优化问题来重构xb:
(2)
式中,λ为正则化参数。基于图像信号的结构特性,许多文献提出了不同的优化算法来求解式(2),并取得了不错的效果,例如平滑投影Landweber算法[5]与基于组稀疏表示的重构算法[6]。但传统的图像压缩感知算法计算量巨大,难以用于实际应用。在图像压缩感知神经网络的研究工作中,则是基于深度学习方法对采样系数与原始图像间的映射关系进行学习。这种方法主要分为两类:1)以ReconNet为代表,应用于图像压缩感知重构的卷积神经网络;2)以CSNet为代表,同时应用于图像压缩感知观测域重构的卷积神经网络。以上提到的两种类型的神经网络结构解决了传统算法中高耗时的缺陷,并取得了不错的恢复效果,但同时也存在着一定的缺陷:1)分块压缩感知框架引起的块效应降低了最终图像的恢复效果;2)缺少针对性的恢复端网络结构限制了网络的重构性能。
2 实现图像压缩感知的多阶段残差学习神经网络
在本节中,将详细讨论本文提出的图像压缩感知神经网络(MSResICS)。MSResICS由3部分组成:采样子网络,初始重构子网络与图像增强子网络,具体网络细节参见图1。
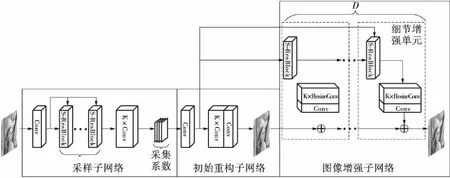
Conv代表卷积层,S-ResBlock代表简化残差学习块,ResizeConv代表插值卷积层
2.1 基于残差学习的采样子网络
为了解决分块压缩感知框架下带来的块效应问题,MSResICS放弃了传统的分块线性映射采样方法,提出一种直接对整幅图像采样的全卷积采样子网络。受文献[10]与[11]启发,文中利用了一种简化残差学习块(S-ResBlock),以使观测值中包含更加丰富的图像信息,且网络参数数据量小,占用内存更少,如图1所示。具体结构参考图2,S-ResBlock和原始ResBlock[21]相比主要存在两点不同:1)删除了批量标准化层(BN),可以更大程度上保留丰富的图像信息,并减少了网络整体计算量;2)恒等映射分支的输入不再为固定输入,选择更加灵活,保证网络输出的观测值包含不同语义维度下的图像信息。在后文中,将展示关于S-ResBlock与ResBlock的对比实验,以进一步验证该结构带来的提升。

相比传统的分块压缩感知和线性映射采样方式,该采样子网络成功避免了块效应问题,并且将非线性结合到了采样过程之中,更有效地对特征信息进行提取,获得信息更加丰富的观测值。
2.2 基于插值卷积的初始重构子网络
在传统图像压缩感知的信号恢复过程中,通常先利用观测值和简单的重构算法获得图像的初始重构,然后利用初始重构图像和观测值,通过较复杂的重构算法进一步提升重构图像的质量。在这种模式下,通过重构算法的迭代逐渐恢复图像中的细节,可以取得优秀的重构效果。文中提出的卷积神经网络重构算法即参考这种策略。

(a)S-ResBlock (b)ResBlock
Conv代表卷积层,ReLU代表线性整流激活函数,BN代表批量标准化层
图2 两种不同的残差学习结构
Fig.2 Two different residual learning block
基于插值卷积(Resize Convolution)[22],文中提出了一个初始重构子网络,用以生成高质量的初始重构图像。如文献[22]所述,插值卷积是对特征图进行上采样的一种直观而简单的方法。在结构上,插值卷积分为两层:首先是一层具有S倍上采样效果的最近邻插值层,再后接一个常用的3×3卷积层以进行特征提取,如图3所示。与另外一种神经网络中常用的上采样方法——反卷积(Deconvolution)相比,插值卷积成功避免了反卷积操作中容易带来的棋盘效应,提升了恢复图像的效果。初始重构子网络主要由3部分结构构成:第1部分是单层卷积层,用来从采样系数中提取高维特征图;第2部分是K个插值卷积,对得到的特征图进行上采样操作,使特征图恢复到原始图像尺寸;最后一部分是一层只有单个卷积核的卷积层,对插值卷积得出的特征图进行整合,输出最后的图像初始重构结果。

Conv代表卷积层
在得出图像的初始重构之后,接下来的工作便以此为基础,逐渐对图像进行精细化的细节恢复。
2.3 多阶段图像增强子网络
为了进一步细化图像结果,文中设计了一个多阶段图像增强子网络,利用初始重构图像和观测值逐渐恢复更多的图像纹理细节。
如图1所示,该多阶段图像增强子网络的基本结构为细节增强单元,其输入是从采样系数中提取的高维特征图。在每个细节增强单元中,先由S-ResBlock对输入进行处理,提取深层特征,再利用插值卷积来重构得出残差图像,与上一级的重构图像进行叠加,得出新的重构图像。通过使用D个细节增强单元,神经网络逐步从采样系数中提取出多幅包含图像细节信息的残差图像,在初始重构图像的基础上不断提升重构质量。最后,在D阶段图像增强后,得出MSResICS的最终输出图像。
与之前的神经网络重构算法相比,文中提出的网络结构利用残差学习作为网络结构基础,对图像进行更加精细的多阶段恢复,恢复的图像细节更加丰富,进一步提升了重构图像质量。
2.4 损失函数
均方误差(MSE)是有效的图像质量客观评判标准。文中在MSResICS网络的训练过程中,同样采用均方误差函数作为网络的优化目标函数:
(3)
式中,xi代表训练集图像,N为训练集样本的个数,θ为网络参数,f(xi,θ)为网络的整体输出。
3 网络实现细节和实验结果
3.1 网络实现和训练细节
考虑到重构性能和内存占用之间的权衡,在实验中,结构参数设置为:R=3,K=2,S=2,D=4。但在计算资源允许的情况下,网络越深,重构效果将会越好。在细节上,还有几点需要注意:1)MSResICS中的每一层卷积层中卷积核的大小均设置为3×3,并且都带有线性整流激活函数(ReLU);2)假如没有明确的描述,每层卷积层都含有64个卷积核;3)关于网络的初始化方法,文中采用了文献[23]给出的针对ReLU激活函数的参数设置策略,以获得最优的效果。
考虑到图像的数量和类别,文中采用MSCOCO数据集[24]作为MSResICS的训练集和验证集:通过从MSCOCO数据集中随机抽取大约10 000张图像,对其进行灰度化处理,并将原图像的中心部分裁剪为256×256大小的子图像。此外,文中同时采用了数据增广对训练数据进行进一步的扩增。在训练过程中,Batchsize的大小设为32,以在训练速度和重构结果上均获得最佳的性能表现。神经网络的优化算法选用的是在许多其他工作中均有较好表现的Adam Optimizer[25],其中的参数设为:β1=0.9,β2=0.999,ε=1×10-8。为了更好地收敛,网络总共训练100个epoch,一个epoch中循环3 000次。在训练中,分别以3种不同的学习率对网络逐渐优化:初始30个epoch学习率为0.000 1,接下来40个epoch为0.000 01,最后30个epoch为 0.000 001。在实验中,网络具体实现的软件框架为:python3.6+tensorflow1.12。关于时间消耗,在GPU-GTX1080ti上,一次完整的网络模型训练大概需要3 d的时间。
3.2 仿真实验结果及性能对比
在本节中,分别设计了3组对比实验,以从多种角度分析说明MSResICS在不同条件下的重构性能表现。
3.2.1 不同算法间的重构性能对比
为了具体分析MSResICS的重构性能表现,文中将MSResICS的图像重构结果与5种具有代表性的图像压缩感知方法进行对比,其中包含两种传统的优化算法与3种基于神经网络的方法,分别是:多假设重构算法(Multi-Hypothesis,MH)[26]、基于组稀疏表示的重构算法[6]、ReconNet[14]、ISTA-Net+[15]和CSNet[19]。多假设重构算法与基于组稀疏表示的算法均是效果比较优秀的传统算法,特别是基于组稀疏表示的重构算法,是目前性能最好的图像压缩感知重构算法。而ReconNet、ISTA-Net+和CSNet都是具有代表性的压缩感知神经网络结构,后两者的恢复效果在神经网络方法中达到了最佳。
为了评估不同算法的重构性能,文中使用由8张标准灰度图像组成的测试组作为评测参照,使用的图像分别来自两个网络来源:https:∥homepages.cae.wisc.edu/~ece533/images/,https:∥www.io.csic.es/PagsPers/JPortilla/image-processing/bls-gsm/63-test-images,具体图像参照图4。文中给出了0.5、0.25、0.125不同采样率下的实验结果。8幅图像的详细峰值信噪比(PSNR)/结构相似性(SSIM)对照结果被统一汇总在表1中。
从表1中可以看出,MSResICS在所有测试情况下的表现均优于其他算法。与优化算法中性能较优秀的基于组稀疏表示的重构算法进行对比,MSResICS在0.125~0.500的采样率下PSNR分别可以提升平均大约3.21、1.81、0.96 dB,而相对于多假设重构算法提升更为明显,分别为5.15、4.48、4.64 dB。从实验结果可以看出,MSResICS的效果不仅超出传统的优化方法,而且大大提高了在低采样率下的图像重构质量。在与基于卷积神经网络的方法对比时,在0.125、0.250、0.500采样率下,MSResICS在PSNR上比Reconnet平均提升了6.25、6.44、7.34 dB,比ISTA-Net+提升大约3.29、2.22、1.32 dB,比CSNet提升2.09、1.96、1.74 dB,展现出其性能的优越性。SSIM作为一种更为先进的衡量图像相似度的指标,在一定程度上进一步体现了算法对于恢复图像的质量好坏。文中提出的MSResICS在SSIM上相较对比算法也都有着不少的提升,并同样在低采样率下的效果更为出色。

(a)Boat (b)Cameraman

(c)Goldhill (d)Lena

(e)House (f)Monarch

(g)Parrot (h)Peppers
在不同的图像上,MSResICS的性能表现也有所不同:例如在细节信息较多的图像Goldhill、House上,MSResICS相较于其他算法的PSNR平均提升分别为3.34、3.51 dB,而在细节信息较少的图像Peppers上平均提升为2.92 dB,在SSIM指标上也保持着类似的规律,证明在细节部分,MSResICS的恢复效果表现更好。在图5和图6中,文中进一步展示了一些更加详细的视觉结果图。在图5 House的0.5采样率恢复图像中,MSResICS在房子烟囱部分的砖块细节恢复上纹理更加明显。在图6 Monarch的0.125采样率恢复图像中对比的5种算法均有较为明显的块效应,而MSResICS的恢复结果整体平滑;而且在细节部分,比如蝴蝶的主体、背景的花卉,MSResICS的恢复图像均更加清晰。从整体上来看,在传统的分块压缩感知框架下,无论是基于优化的算法还是基于神经网络的算法,恢复图像中图像块的边界容易出现不自然的分界线,尤其在低采样率下这个问题尤为明显。文中提出的MSResICS则成功地避免了这个问题,在重构图像整体的视觉效果上都均匀平滑。除此之外,在细节的恢复质量对比上,MSResICS也比其他算法保留了更多的高频信息和边缘信息,纹理更加清晰。同时,文中还将MSResICS与文献[18]中提出的MSRNet的部分结果进行了一定的对比,参照表2,可以看出MSResICS在重构图像的PSNR上要远远优于MSRNet。
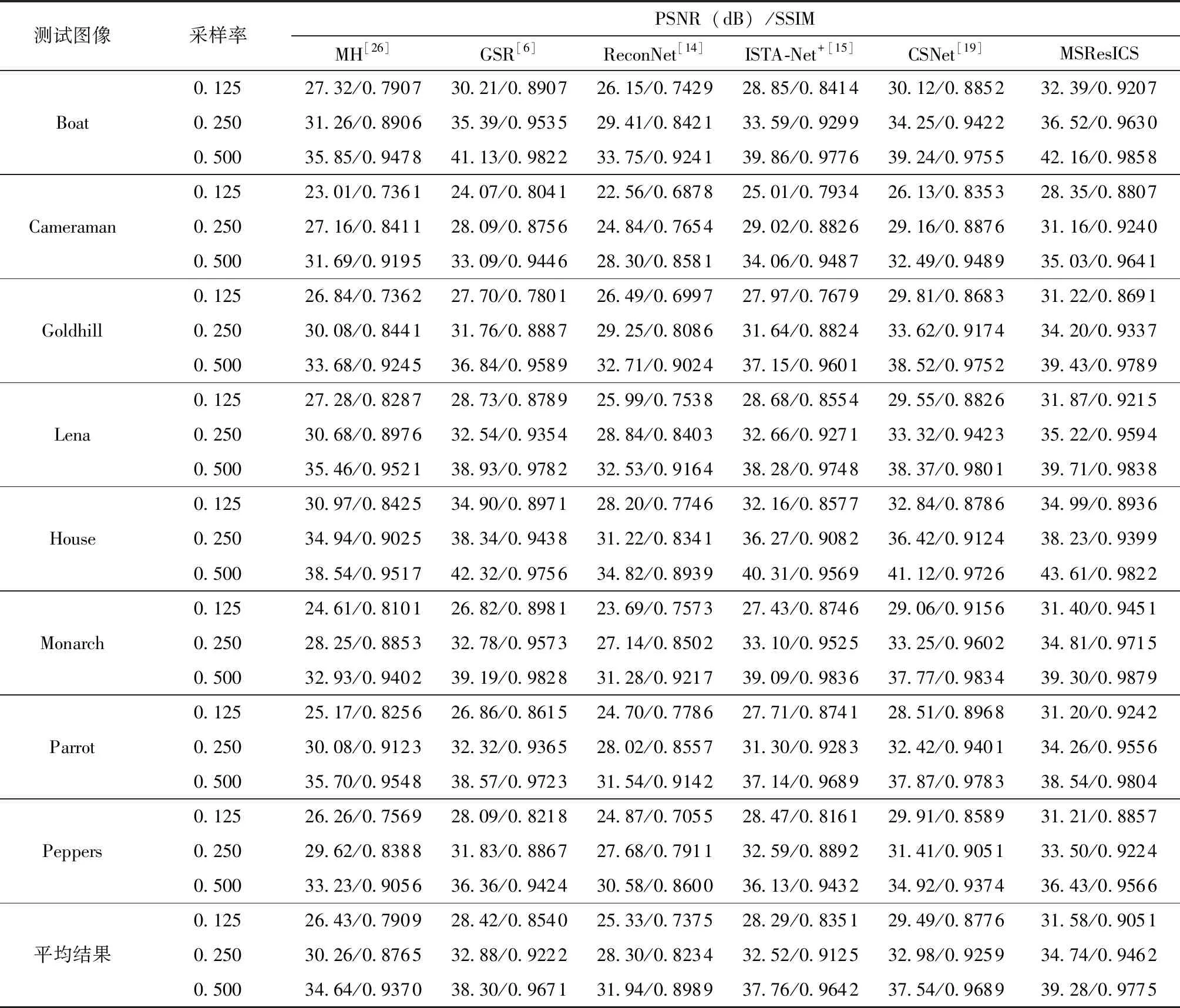
表1 MSResICS与几种不同重构算法的PSNR/SSIM恢复结果

MH/38.54 GSR/42.32 ReconNet/34.82 ISTA-Net+/40.31 CSNet/41.12 MSResICS/43.61 House/PSNR
图5 0.5采样率下不同算法对图像House的视觉恢复图像
Fig.5 Visual recovery images of different methods on image House under sampling ratio 0.5

MH/24.61 GSR/26.52 ReconNet/23.69 ISTA-Net+/27.43 CSNet/29.06 MSResICS/31.40 Monarch/PSNR
图6 0.125采样率下不同算法对图像Monarch的视觉恢复图像
Fig.6 Visual recovery images of different methods on image Monarch under sampling ratio 0.125
表2 0.25采样率下MSResICS与MSRNet恢复结果PSNR对比
Table 2 Comparison of recovery PSNR results for MSResICS and MSRNet with sampling ratio 0.25

重构算法PSNR/dBBoatLenaMonarchPeppersMSRNet[18]30.7430.2128.9029.51MSResICS36.5235.2234.8133.50
3.2.2 在小数据集上的重构性能对比
为了公平的对比,进一步考察MSResICS在小数据集上的表现,文中基于文献[19]中使用到的BSDS500数据集[27]对MSResICS进行了重新训练,其中训练集总共由400张图片构成,分别来自BSDS500中的训练集(200张图片)与测试集(200张图片),验证集则由来自BSDS500验证集的100张图片构成。除数据集不同外,其余训练设置则与上述实验保持一致。表3中展示了在不同采样率下,基于BSDS500数据集训练的MSResICS对上述八幅图像的平均恢复结果,并以CSNet作为基准进行对比。在低采样率的情况下,MSResICS(BSDS500)在恢复图像的PSNR与SSIM上相较于CSNet仍然有明显提升。但与基于MSCOCO训练的版本对比,MSResICS(BSDS500)的恢复图像质量有所下降。产生以上结果的主要原因为:MSResICS在训练过程中,输入的是整幅图像,需要的图片量更为庞大,而CSNet对于图像分块进行训练,在较小的图片数据集上即可取得不错的效果;同时,由于MSResICS的输入是整幅图像的原因,它克服了CSNet在低采样率下恢复图像中的块效应问题,提升了恢复图像的质量。
表3 基于BSDS500训练的MSResICS恢复结果平均PSNR/SSIM比较
Table 3 Comparison of recovery average PSNR/SSIM results on MSResICS trained on BSDS500

训练方式PSNR(dB)/SSIM0.1251)0.2501)0.5001)CSNet29.49/0.877632.98/0.925937.54/0.9689MSResICS(BSDS500)31.45/0.902433.34/0.929637.27/0.9654MSResICS(MSCOCO)31.58/0.905134.74/0.946239.28/0.9775
1)为采样率。
3.2.3 不同网络结构的重构性能对比
在保证网络其余结构一致的情况下,表4中展示了S-ResBlock与原版ResBlock在不同采样率下的对比实验结果。在不同图像上,S-ResBlock的效果均优于ResBlock,PSNR结果提升0.6~1.2 dB,SSIM大约提升0.02~0.06,证实了前者针对压缩感知任务的有效性。
表4 S-ResBlock与ResBlock结构恢复结果PSNR/SSIM比较
Table 4 Comparison of recovery PSNR/SSIM results between S-ResBlock and ResBlock structures

测试图像采样率PSNR(dB)/SSIMResBlockS-ResblockCameraman0.12527.41/0.820728.35/0.88070.25030.02/0.892531.16/0.92400.50034.37/0.949235.03/0.9641Lena0.12530.71/0.915631.87/0.92150.25034.59/0.950135.22/0.95940.50038.82/0.977539.71/0.9838House0.12533.81/0.882334.99/0.89360.25037.52/0.921538.23/0.93990.50042.46/0.975443.61/0.9822
为了验证采样子网络和图像增强子网络对重构性能的影响,本小节在保持训练条件不变的情况下重新训练了两种网络结构,分别为:①随机高斯观测+初始重构子网络+图像增强子网络,②采样子网络+初始重构子网络,并与完整的MSResICS进行重构效果上的对比。表5中给出了对应的实验对
表5 不同子网络结构设定下神经网络之间的恢复结果PSNR/SSIM比较
Table 5 Comparison of recovery PSNR/SSIM results between networks with different subnetwork settings

测试图像采样率PSNR(dB)/SSIM①随机高斯观测+初始重构子网络+图像增强子网络②采样子网络+初始重构子网络完整结构Peppers0.12527.93/0.812230.48/0.876931.21/0.88570.25030.18/0.842632.85/0.915433.50/0.92240.50033.37/0.921235.62/0.954036.43/0.9566Monarch0.12526.15/0.821530.62/0.933531.40/0.94510.25029.11/0.895533.95/0.966534.81/0.97150.50033.41/0.954937.77/0.985239.30/0.9879Parrot0.12527.94/0.882229.91/0.916231.20/0.92420.25030.29/0.917133.36/0.950134.26/0.95560.50034.66/0.967637.62/0.978738.54/0.9804
比结果。在不同采样率下,完整的MSResICS都要优于两组对比试验:恢复图像PSNR/SSIM相较于①平均提升4.2 dB/0.057,而对比②平均提升0.94 dB/0.006。部分视觉效果图对比如图7所示,图中3列从左至右分别为①、②和完整结构3种情况下的重构图像。可以看出,与两个对照组相比,完整结构的网络在细节和轮廓上的恢复效果均较好,例如Goldhill的远景部分,Lena的帽子部分。以上的结果表明,采样子网络对于网络的性能有着关键的影响,相比于传统高斯采样矩阵,其大大强化了图像压缩感知采样过程中的效率,提升了网络的重构效果;而图像增强子网络在初始重构图像的基础上进一步增强了恢复图像中的细节信息,提高了最终恢复图像的质量。

(a)Goldhill/随机高斯矩阵观测 采样率=0.5/PSNR=34.31/SSIM=0.934 7

(b)Goldhill/除去图像增强子网络 采样率=0.5/PSNR=38.77/SSIM=0.977 4

(c)Goldhill/完整结构 采样率=0.5/PSNR=39.43/SSIM=0.978 9

(d)Lena/随机高斯矩阵观测 采样率=0.25/PSNR=31.24/SSIM=0.904 2

(e)Lena/除去图像增强子网络 采样率=0.25/PSNR=33.95/SSIM=0.950 1

(f)Lena/完整结构 采样率=0.25/PSNR=35.22/SSIM=0.959 4
4 结论
在文中,提出了一种新颖的网络结构——MSResICS来处理图像压缩感知中的两个重要问题:采样和恢复。首先,文中放弃了在一些情况下会限制恢复性能的传统分块压缩感知框架,提出了基于残差学习的全卷积采样方法,并运用插值卷积,设计了对应的初始重构子网络。为了细致深入的图像恢复,基于前两个子网络的工作,文中进一步引入了多阶段图像增强子网络以稳定地提升重构图像质量。通过end-to-end的训练方式,提出的MSResICS获得了令人满意的重构结果。与几种最先进的重构算法相比,MSResICS在恢复图像的PSNR上平均提高了2~3db,在视觉效果上也有着不错的提升。在未来的工作,作者将尝试将MSResICS结合到视频压缩感知框架下,并寻求更多的突破。
