基于稀疏算法的大型转子多工况轴心轨迹提纯
2020-06-17郭明军李伟光杨期江赵学智
郭明军 李伟光† 杨期江 赵学智
(1.华南理工大学 机械与汽车工程学院,广东 广州 510640;2.广州航海学院 轮机工程学院,广东 广州 510725)
轴承和转子是旋转机械中密不可分的关键部件,在工作过程中相互作用,共同决定着机器的稳定性、可靠性及安全性,因此,通常把转子、轴承和轴承座作为一个整体(即转子系统)来探讨其动力学行为[1]。工程实际中,由于转子系统结构及运行环境的复杂性,振动噪声时有发生,而过大的振动会引发零部件间的碰磨、不对中等故障,严重时还可能引发重大安全事故[2]。因此,对转子系统进行状态监测和故障诊断显得尤为重要。通过同一轴截面相互垂直布置的两个位移传感器获取的转子振动位移信号合成的轴心轨迹,包含了旋转机械丰富的运行状态信息,可用于转子的故障诊断[3]。
然而,由于工业现场环境的复杂性,实测的振动信号不可避免地会受到诸多干扰因素的影响,从而使得转子的轴心轨迹形状杂乱无章而无法判断故障类型。小波变换和小波包变换[3]、经验模态分解算法(Empirical Mode Decomposition,EMD)[4]等方法已经相继用于转子轴心轨迹的提纯。但是,小波变换容易造成细节信号的丢失,小波包变换会发生频谱泄露,EMD也存在模态混叠等固有缺陷[5]。
近年来,稀疏分解(Sparse Decomposition,SD)技术已成为分析非平稳信号的重要工具,并成功应用于压缩感知[6]、图像处理[7]、故障诊断[8]、参数估计[9]等领域。Lustig等[6]提出了一种实用的非相干欠采样方案,并利用稀疏分解理论对其混叠干扰进行了分析。Duarte等[7]基于稀疏表征理论提出了一种通过压缩采样实现单像素成像的方法。He等[8]提出一种基于匹配追踪的齿轮箱耦合调制信号分离方法,克服了针对齿轮箱的传统特征提取方法忽略稳态调制成分的缺陷。Ou等[9]提出一种基于稀疏分解的快速算法,并将其用于多项式相位信号的参数估计,与其他传统的稀疏分解算法相比,该算法可极大地提高参数估计的准确性。
文中针对实测转子振动信号受噪声干扰的问题,结合旋转机械振动信号的特征,提出一种基于稀疏分解理论的故障特征频率提取算法(即稀疏算法),并通过对仿真信号的分析,验证其在轴心轨迹提纯方面的有效性;最后,将此稀疏算法用于提纯大型滑动轴承转子多转速工况下的轴心轨迹,成功识别了转子在各工况下的故障类型。
1 稀疏分解基本理论
稀疏分解是指用较少的基本信号的线性组合来表达原始信号,这些基本信号被称为原子。稀疏分解理论包括过完备字典集构建和稀疏系数求解两个部分。
1.1 过完备字典集构建
所谓过完备字典是指由个数超过信号维数的原子所组成的集合,主要包括分析字典和学习字典两种类型。前者是指采用一系列参数化的波形函数所构造的字典,如Heaviside字典、Dirac字典、Gabor字典和余弦字典等,后者则是通过MOD、K-SVD等算法学习得到的字典[10- 13]。
鉴于本文的研究对象是大型滑动轴承试验台,其主轴振动信号具有典型的周期性,除了转速的基频信号外,还会出现二倍频及高次谐波等周期性成分,而余弦函数可以很好地表达信号的周期性,根据上述特点,采用余弦波模型来构建余弦字典,其原子模型如下:
(1)
式中,fi和ti(i=1,2,…,m)分别为频率和时间参数,αi为相位参数。对式(1)进行归一化处理,有:‖di‖=1。
首先,假设f为某个待提取的频率分量,根据振动信号的频谱特征,在f的邻域[f-Δf,f+Δf]内,将fi进行m等分,有
fi=f-Δf+2Δf/m
(2)
(3)
最后,在N维Hilbert空间H∈RN,由所有这些不同参数的原子构成具有m×n个原子的过完备字典集,即有
D={di,i=1,2,…,m×n}
(4)
1.2 稀疏系数求解
从过完备字典中为原始信号寻找最稀疏系数的方法有多种,而贪婪算法和松弛算法是其中最为经典的两种,前者包括匹配追踪及其改进算法、阈值法等,后者包括迭代加权最小二乘法及基追踪等[14- 15]。匹配追踪算法因具有良好的抗噪性,已被广泛应用于齿轮箱、轴承等机械故障诊断领域,文中也将采用该算法进行稀疏系数的求解。
假设y为H∈RN中的任意信号,根据内积最大原则,先从过完备字典集中选出与信号y最匹配的原子d1,即有
〈y,d1〉>〈y,di〉,i≠1,di∈D
(5)
于是,经过第一次匹配,信号可分解为
y=〈y,d1〉d1+R1y
(6)
式中,R1y为第一次分解后的剩余量,且满足d1与R1y正交。故有
(7)
再对R1y进行类似的匹配,可选出第2个最匹配的原子,依此类推,经过k次匹配之后有
(8)
式中,Rky为经k次匹配之后的残余分量,其绝对值随着k的增大而迅速衰减为0[14]。在给定精度条件下,原始信号可以近似为
(9)
1.3 实例分析
为了验证文中提出的稀疏算法的有效性,按下式构造仿真轴心轨迹:
(10)
式中,x(t)、y(t)分别表示相互垂直的位移信号,f为转频,a={a1(t),a2(t),a3(t)}、α={α1,α2,α3}分别为信号x(t)的1、2、3倍频的幅值和相位参数,b={b1(t),b2(t),b3(t)}、β={β1,β2,β3}分别为信号y(t)的1、2、3倍频的幅值和相位参数,e={e1(t),e2(t)}为高斯白噪声。
按照表1中的参数取值并根据式(10)可构造出如图1所示的含噪信号。由这些信号合成的轴心轨迹如图2(b)所示。对比图2(a)所示的理想轴心轨迹可知,此时的轴心轨迹已变得杂乱无章。

表1 仿真信号的基本参数Table 1 Basic parameters of simulated signals
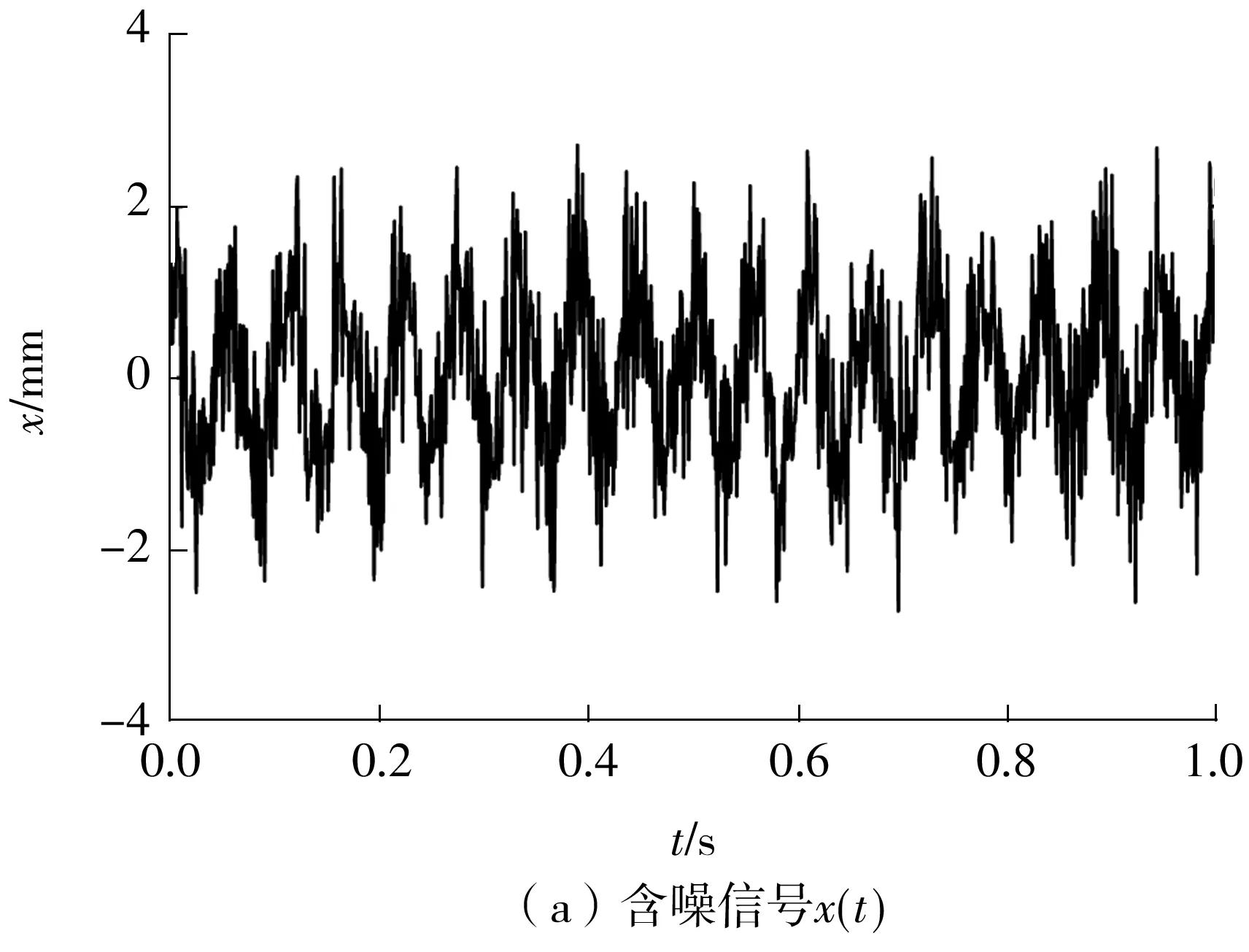
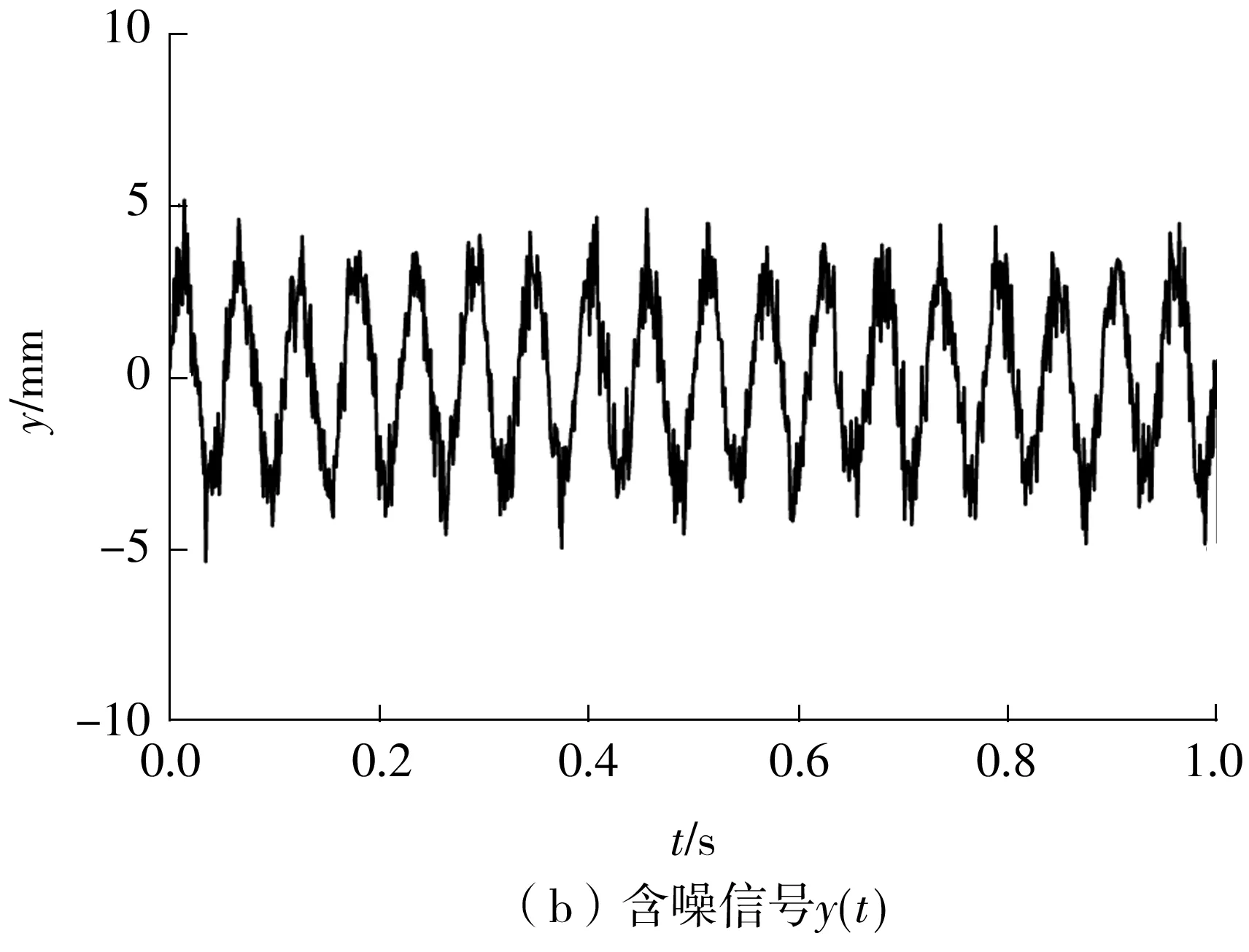
图1 仿真含噪信号Fig.1 Simulated noise signals
采用文中提出的稀疏算法对图2中的轴心轨迹进行提纯时,频率和相位参数的等分间隔Δ对算法计算量、滤波效果的影响较大。为确定其合适的取值范围,令其取不同的数值,采用运行时间t来衡量程序的计算量,用信噪比(Signal-to-Noise Ratio,SNR)和均方根误差(Root Mean Square Error,RMSE)

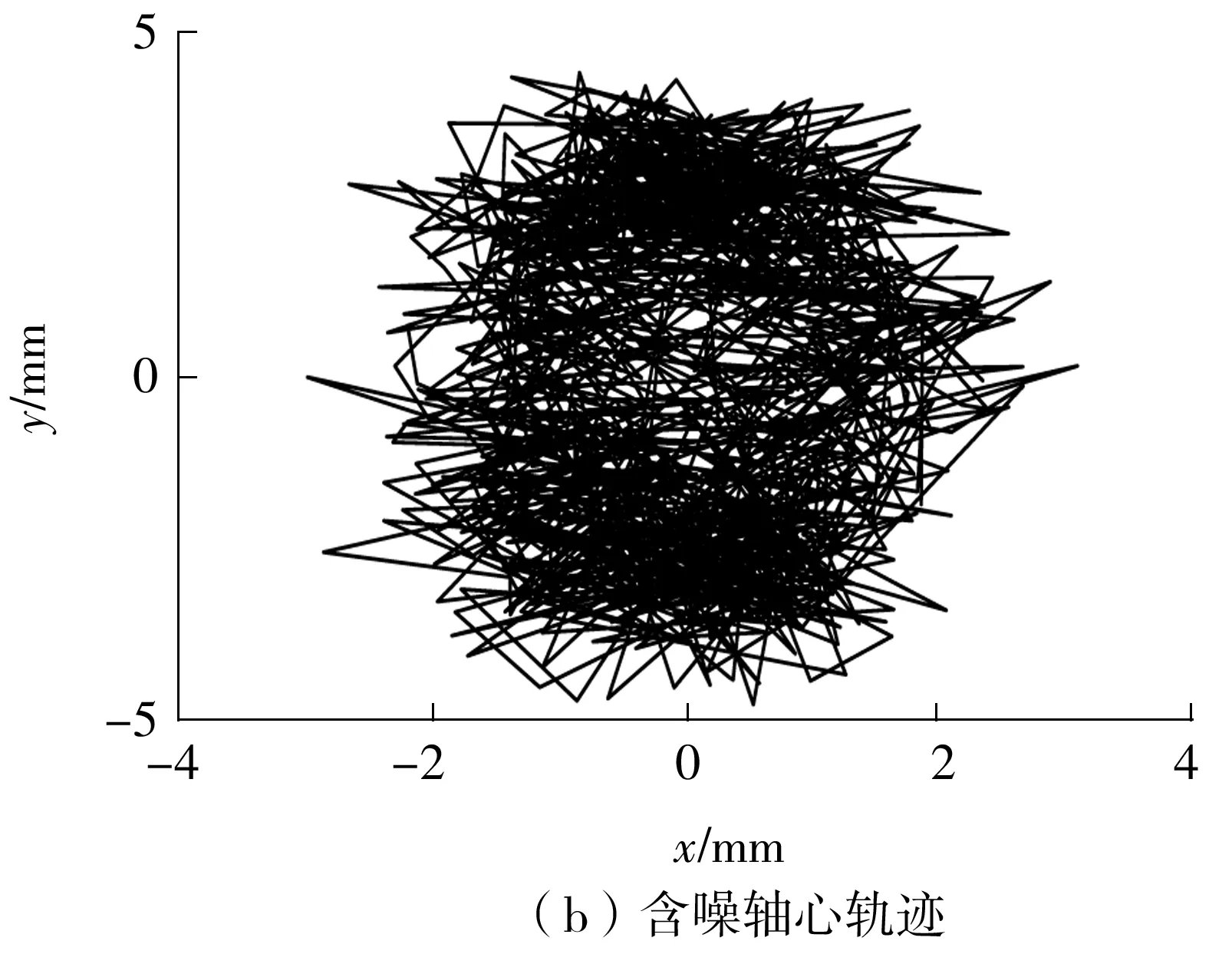
图2 仿真椭圆形轴心轨迹Fig.2 Simulated elliptic axis trajectories
来评估算法的滤波效果。SNR的表达式如下:
(11)
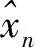
RMSE代表提纯信号与原始真实信号之间的差值,其表达式如下:
(12)
RMSE值越小代表信号的滤波效果越好。
表2为Δ取不同值时的信号提纯结果,由表可知:Δ在区间[0.05,0.50]内取值时,SNR较大且RMSE较小,信号的滤波效果较理想;当Δ取0.01时,SNR和RMSE与Δ在[0.05,0.50]内取值时相差不大,而其计算量约为Δ取0.05时的72倍之多;当Δ取1.00时,虽然计算时间有所缩短,但是SNR和RMSE却下降了许多,说明此时的信号滤波效果并不理想。
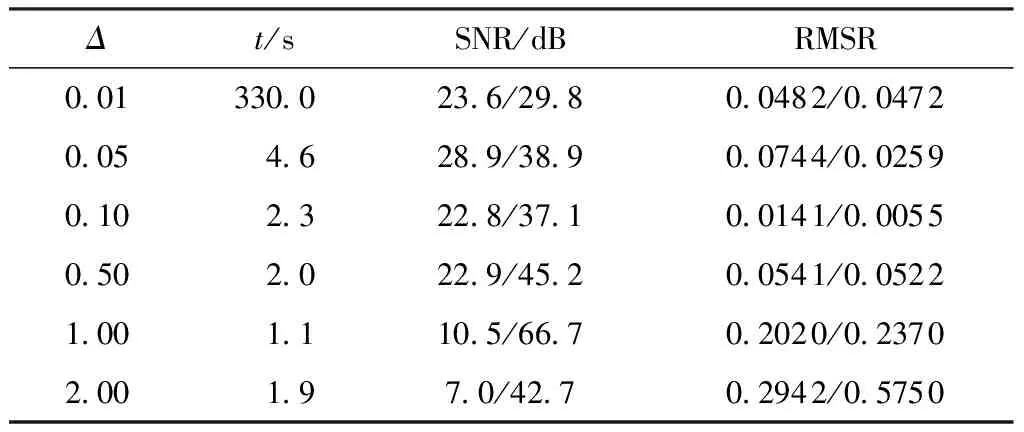
表2 含噪信号提纯结果Table 2 Purification results of noisy signals
综上所述,频率和相位参数的间隔在[0.05,0.50]内取值较合适,过大的取值会造成滤波效果变差,过小的取值则会极大地增加计算量。
对于本例,取Δ为0.05时,可构造包含320×628个原子的过完备字典集。基于所构造的字典集,采用稀疏算法对图2(b)中的轴心轨迹进行提纯,结果如图3所示。对比图1和3可知,提纯效果很好,从而验证了稀疏算法的有效性。限于篇幅,文中只给出了椭圆形轴心轨迹的提纯结果,经反复验证,文中方法同样适用于香蕉形、外8、内8及花瓣形等其他故障类型轴心轨迹的提纯。
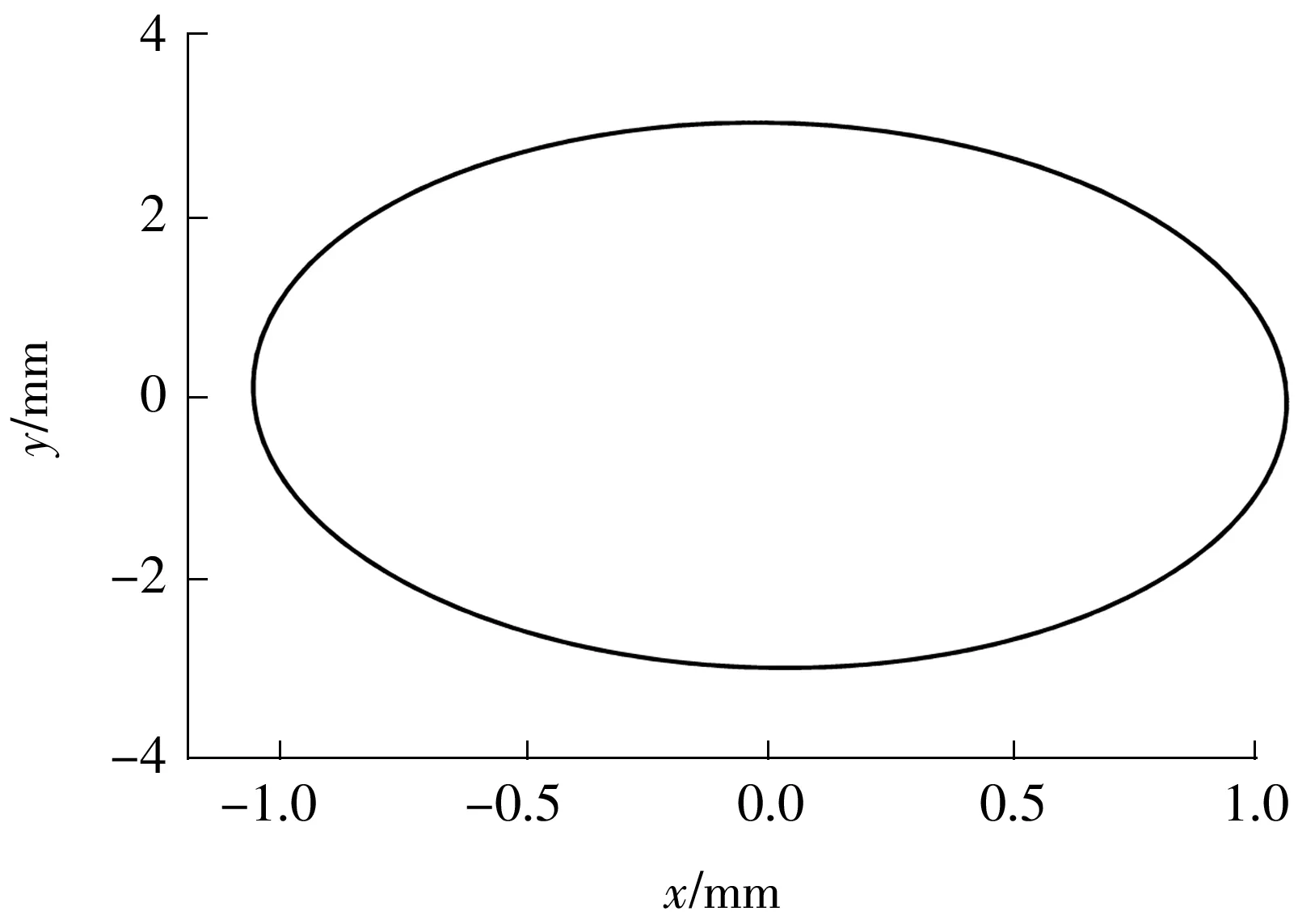
图3 轴心轨迹的提纯结果Fig.3 Purified axis trajectory
2 试验验证
2.1 试验说明
图4所示为大型滑动轴承试验台,它由前后两个试验轴承、轴承支座、主轴、大功率伺服电机、推力轴承机构、基座等组成,其中试验轴承安装在主轴两端的轴承座内。该装置可以模拟汽轮机的实际运行工况,其工作转速最高可达4 000 r/min。
试验装置搭建完成初期,试验台各零部件需要磨合,可能会出现各种故障,可通过采集试验装置各部分的振动信号进行分析。共安装了4个位移传感器,用来监测A、B轴截面两边斜45°方向的位移,所测得的信号依次标记为D1、D2、D3、D4。转速传感器(n)安装在B端轴颈外侧。表3为试验的基本参数。

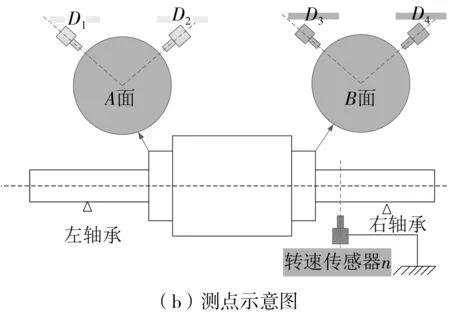
图4 试验装置及其测点示意图Fig.4 Rotor test-bed and its measuring points

表3 试验基本参数Table 3 Basic test parameters
2.2 数据说明
试验装置调试完成并且无异常后,由低转速逐步提升到各工作转速,对每一种转速,稳定运行5 min后,再由LMS数据采集系统来采集主轴的位移信号。
限于篇幅,文中仅以某次试验中1 080 r/min(18 Hz)转速工况下采集的转子A端的位移信号为例来去除直流分量,结果见图5,其中图5(a)、5(b)为信号的时域波形。由图可见,位移信号因受到了严重的噪声干扰而使得波形复杂混乱;5(c)、5(d)为信号的频谱图,从图可知,位移信号的频率成分众多,如1X、2X、3X、5X、9X等,同时还存在工频成分及随机噪声的干扰。其他转速情况下采集的信号都是在相同工况下采集的,因而信号特点比较类似。
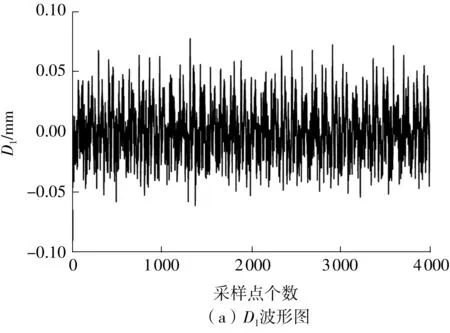
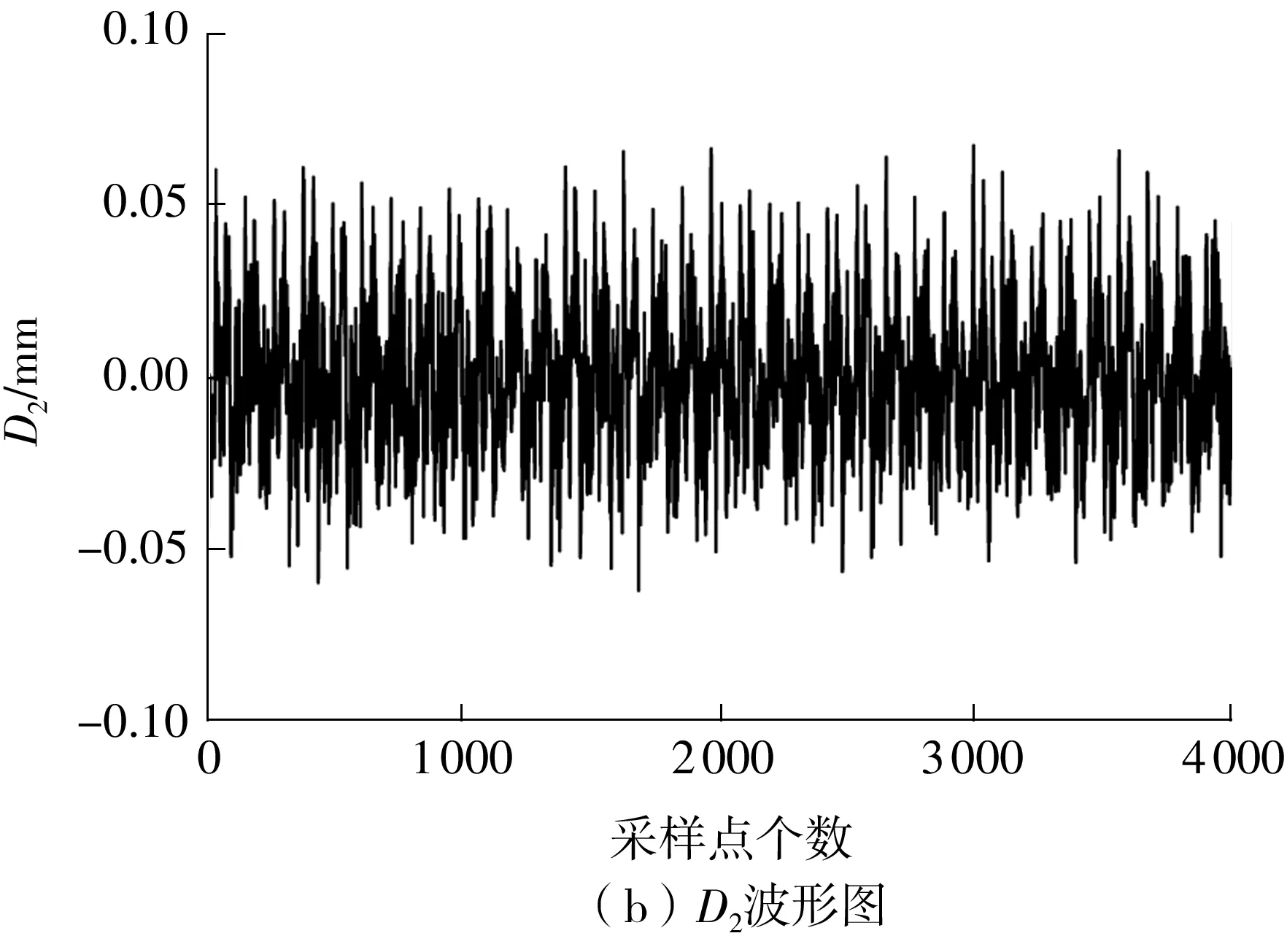
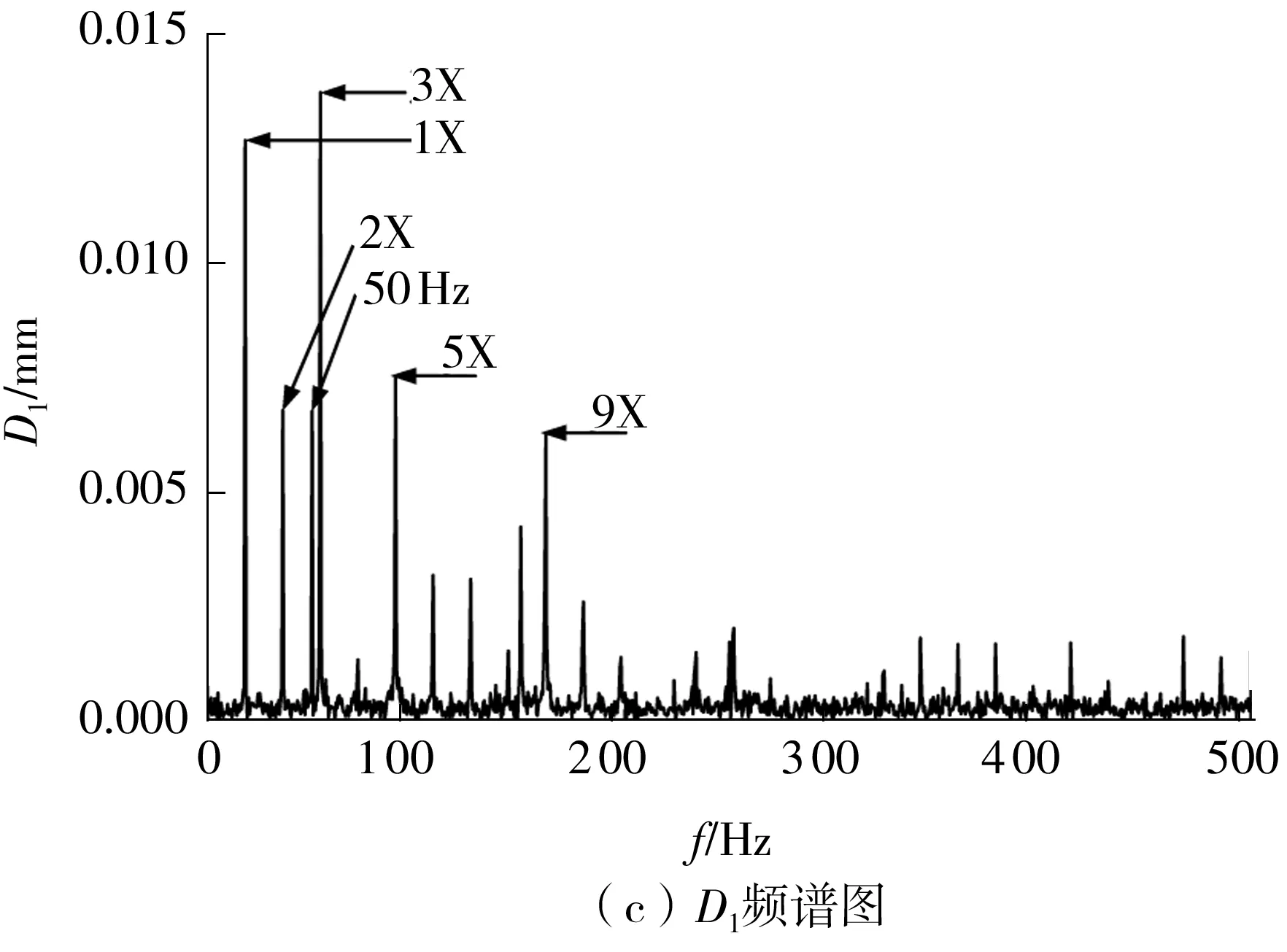
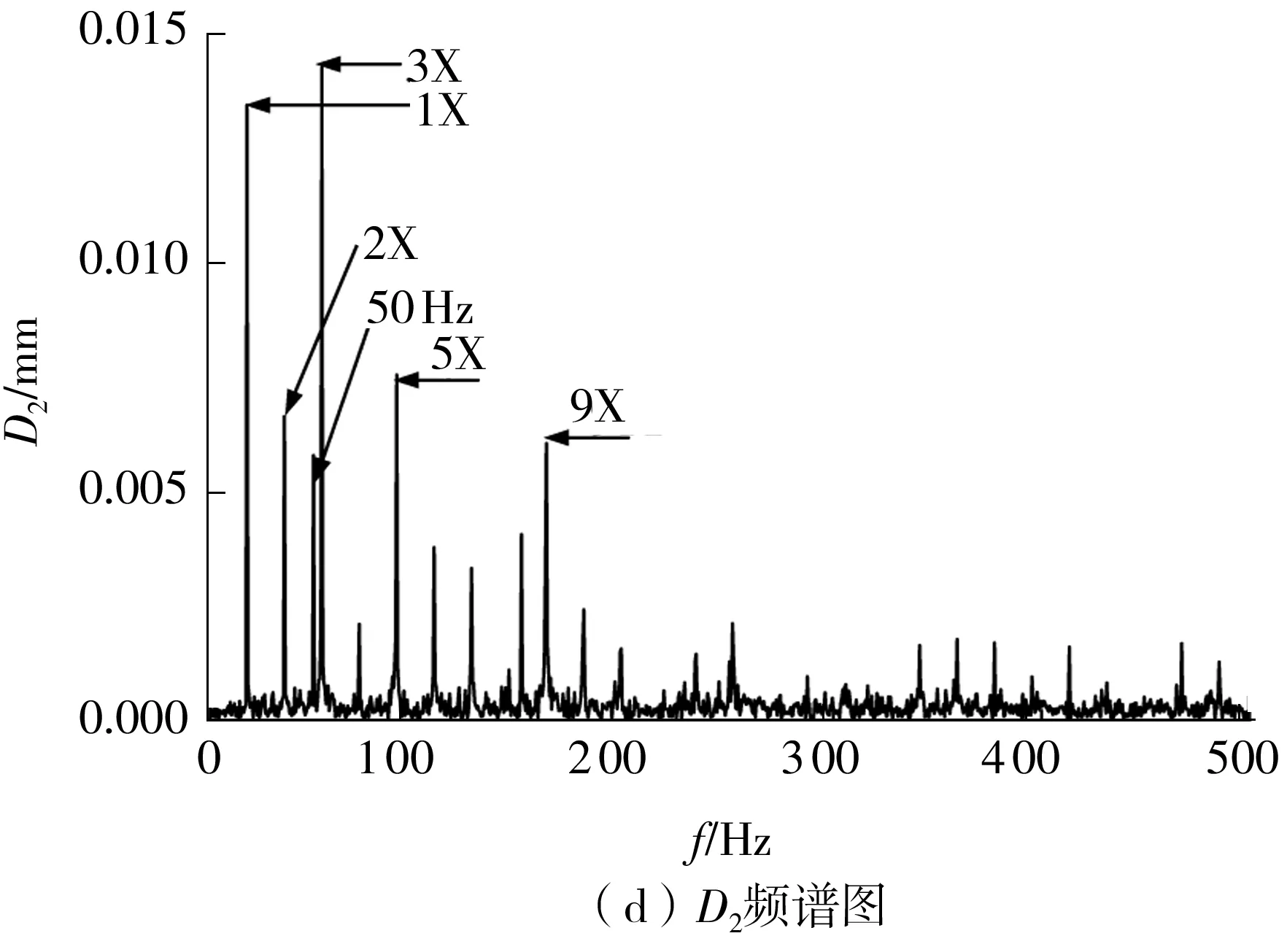
图5 A端的位移信号Fig.5 Displacement signals on face A
3 轴心轨迹提纯
旋转机械的不同轴心轨迹形状对应着不同的故障类型,如“香蕉”形对应转子的轻微不对中故障,外8字形对应严重不对中故障,而花瓣形对应动静件碰磨故障等[3,10],可结合实测的转子直流分量及动压润滑理论等对故障原因进行分析。
3.1 直流分量分析
试验台主轴两端测得的直流分量随转速的变化如图6所示。图6(a)所示为A端直流分量随转速的变化,由图可知,随着转速的升高,D1方向的直流分量不断减小,反映了主轴位置不断往D1方向靠近。对于D2方向,当转速由0 r/min逐渐升高到480 r/min时,直流分量变大,反映了主轴位置远离D2方向,说明此过程中动压油膜逐渐形成而使得主轴慢慢抬升;当转速由480 r/min逐渐升高到2 280 r/min时,该方向的直流分量变小,说明主轴在抬升的过程中油膜的最小厚度变大,轴承的泄油量增大,最终使得油膜承载力变小而导致主轴位置开始慢慢下降;当转速由2 280 r/min逐渐升高到3 960 r/min时,该方向的直流分量又开始增大,说明主轴又开始慢慢抬升。
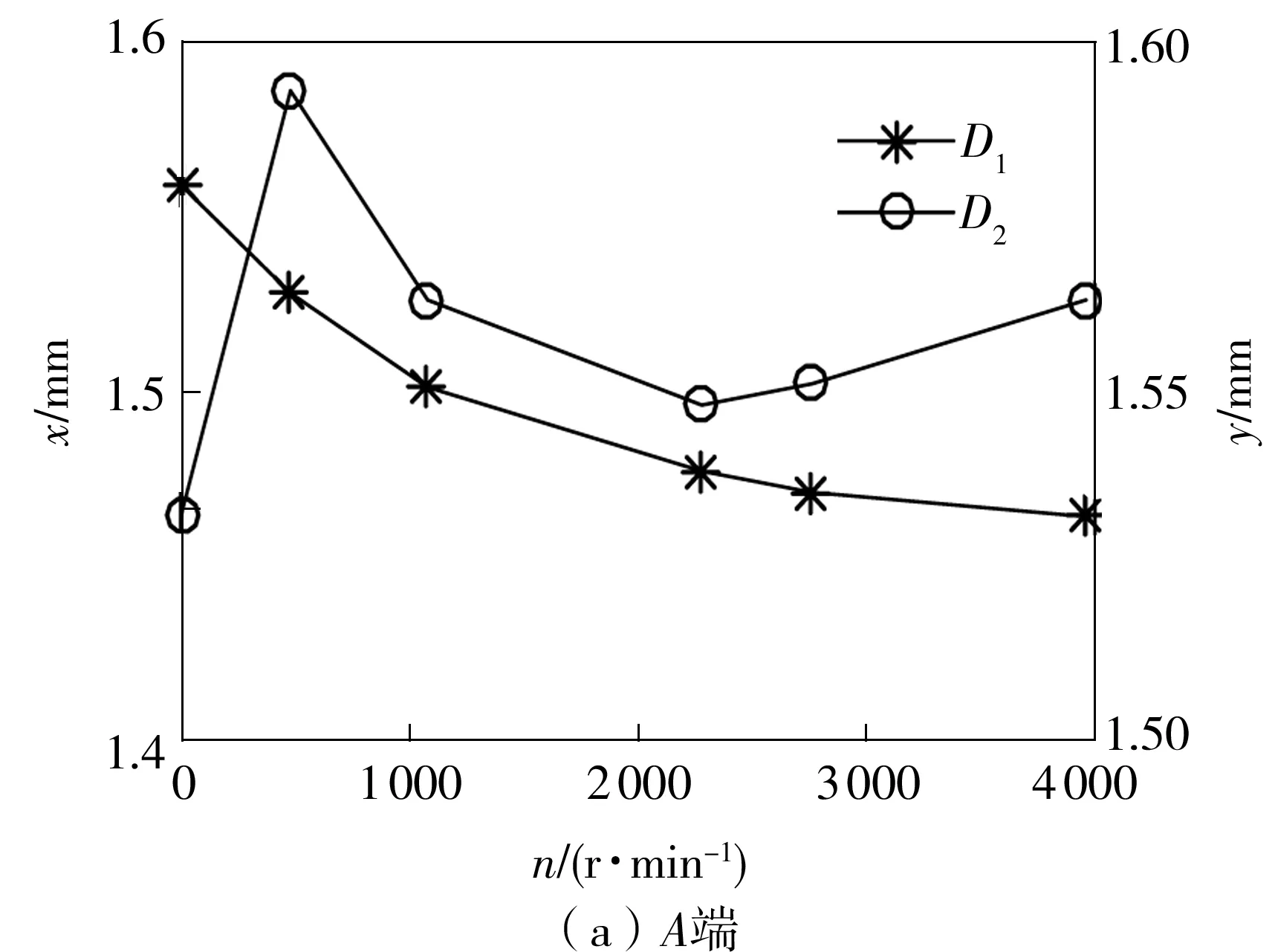
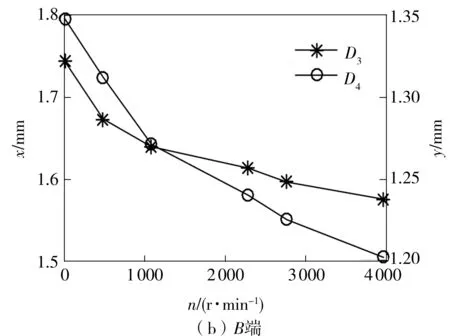
图6 直流分量的变化趋势Fig.6 Variation trends of DC components
图6(b)所示为B端直流分量随转速的变化,由图可知,随着转速的升高,D3、D4方向的直流分量都不断减小,说明B端主轴在整个升速过程中其位置不断地往上抬升。
为了更直观地反映主轴位置的变化,绘制主轴位置变化趋势图,结果如图7所示。由图7(a)可知,A端轴颈的位置在整个升速过程中先后经历了升高—降低—再升高的位置变化过程,这与根据图6(a)数据分析所得的结果一致。由图7(b)可知,自由端的轴颈位置在整个升速过程中始终在抬升,这与根据图6(b)数据分析所得的结果相符合。
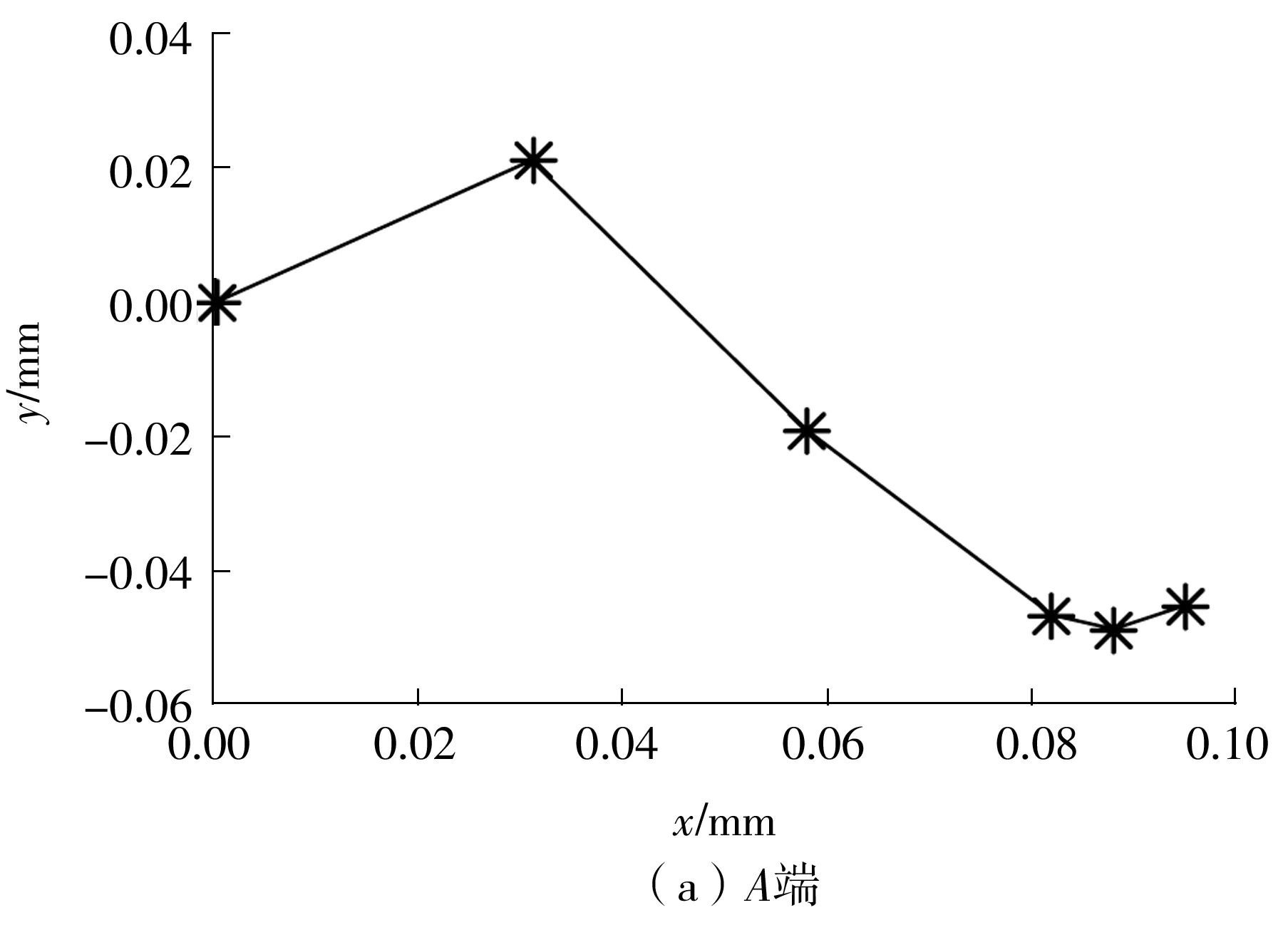
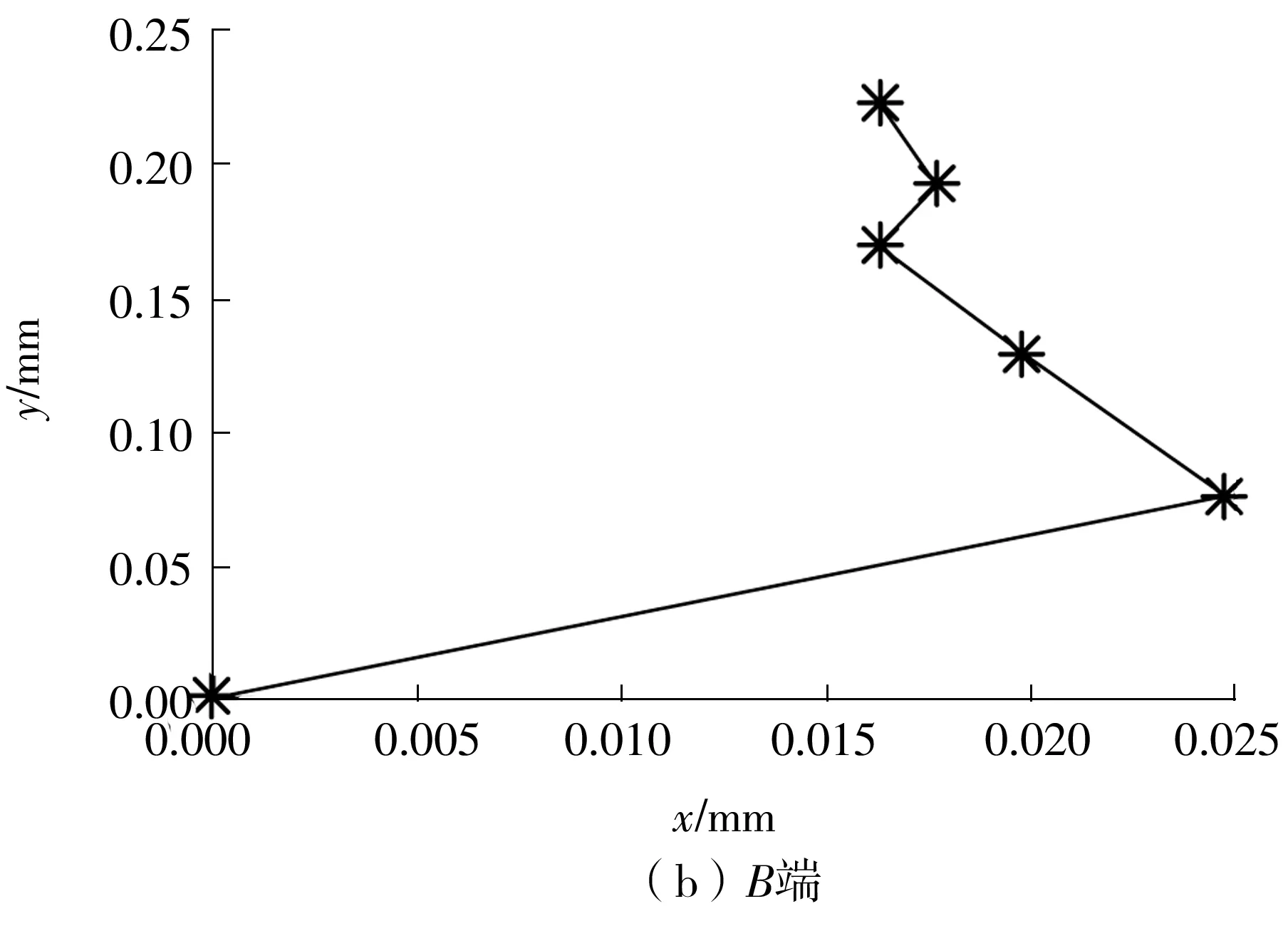
图7 主轴位置的变化趋势Fig.7 Variation trends of spindle position
3.2 轴心轨迹提纯
以1 080 r/min工况下测得的数据为例,由图5的两组位移信号直接合成的轴心轨迹如图8所示。由图8可知,利用原始信号合成的轴心轨迹杂乱无章。因此,采用文中提出的稀疏算法对图5中的信号进行提纯。由于振动信号的随机性,在试验之前无法获知其确切的表达式,故在此处仅以程序运行时间来衡量参数选择的优劣。表4为频率和相位参数在区间[0.05,0.50]内取不同值时的程序运行时间,由表可知,该实测信号参数的合适划分间隔取值范围为[0.10,0.50]。
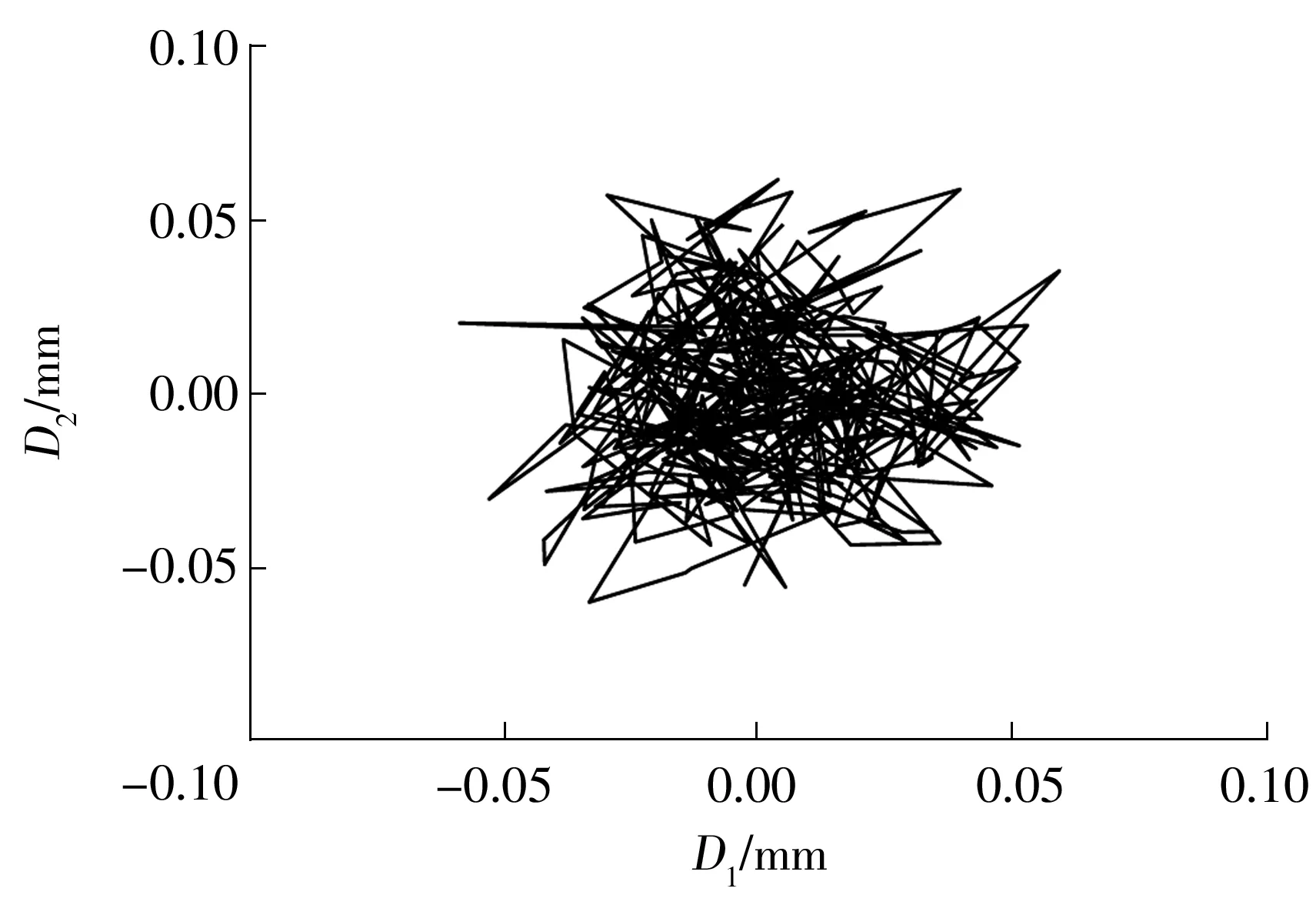
图8 1 080 r/min工况下的原始轴心轨迹Fig.8 Original axis trajectory at a rotate speed of 1 080 r/min
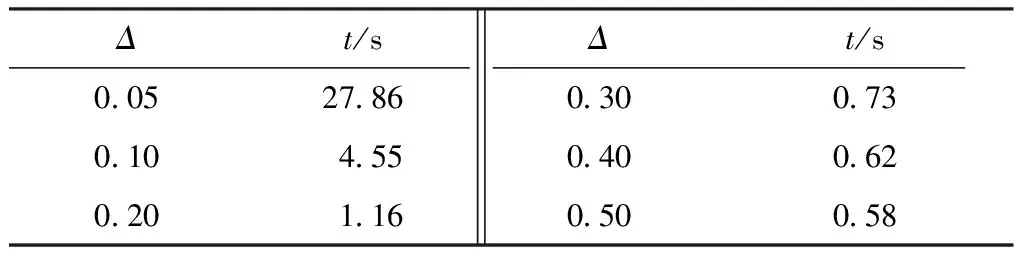
表4 试验信号提纯结果Table 4 Purification results of test signals
为减少计算时间成本,本次试验都取Δ为0.50,此时,可构造包含104×628个原子的过完备字典集。基于所构造的字典集,采用稀疏算法对图5中的信号进行提纯,结果如图9所示。由图9可知,提纯信号的波形十分清晰,而其频谱图证实了提取到的确实为信号的基频(1X)和三倍频成分(3X),这也验证了文中提出的稀疏算法在特征频率提取及信号提纯中的有效性。
由图9中的提纯信号合成的轴心轨迹如图10(a)所示,该轴心轨迹为明显的“花瓣形”,这说明了因轴瓦摆动而引起的转子的复杂运动现象。10(b)所示为采用合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)滤波的提纯轴心轨迹,其外形比较杂乱,这是由于原始振动信号包含了丰富的频率成分,而EEMD并不能充分抑制此类复杂信号的模态混叠现象,这才使得提纯的信号中混入了其他的频率成分,从而令轴心轨迹杂乱无章。
综上所述,文中提出的稀疏算法在此类大型转子轴心轨迹的提纯中更具优势,能有效提取出振动信号的主要特征。
图11为采用稀疏算法对表3中其他转速工况的信号进行提纯得到的提纯轴心轨迹,其中A端的轴心轨迹由提纯的D1和D2合成,B端的轴心轨迹则由提纯的D3和D4合成。
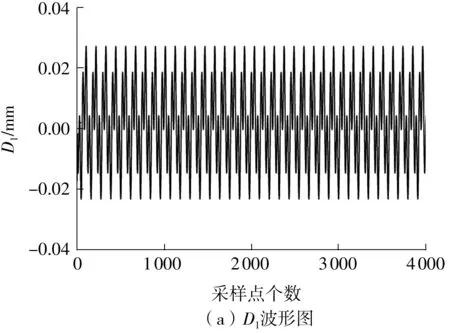
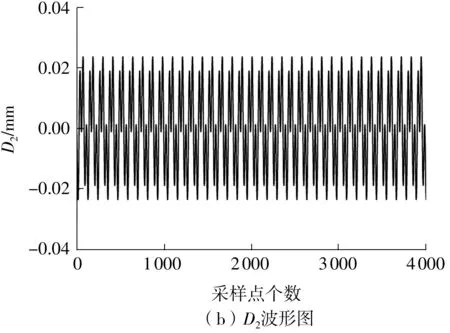
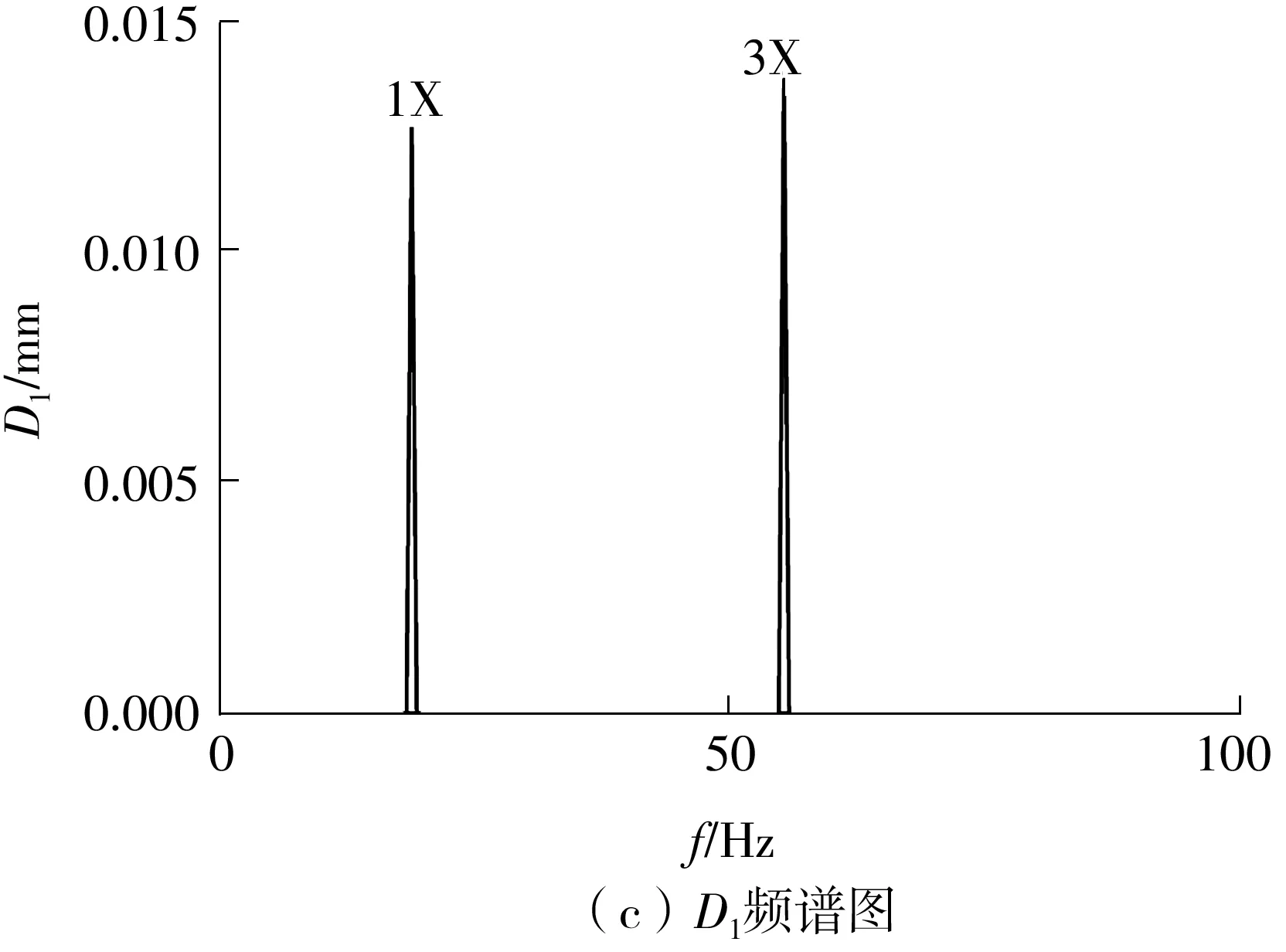
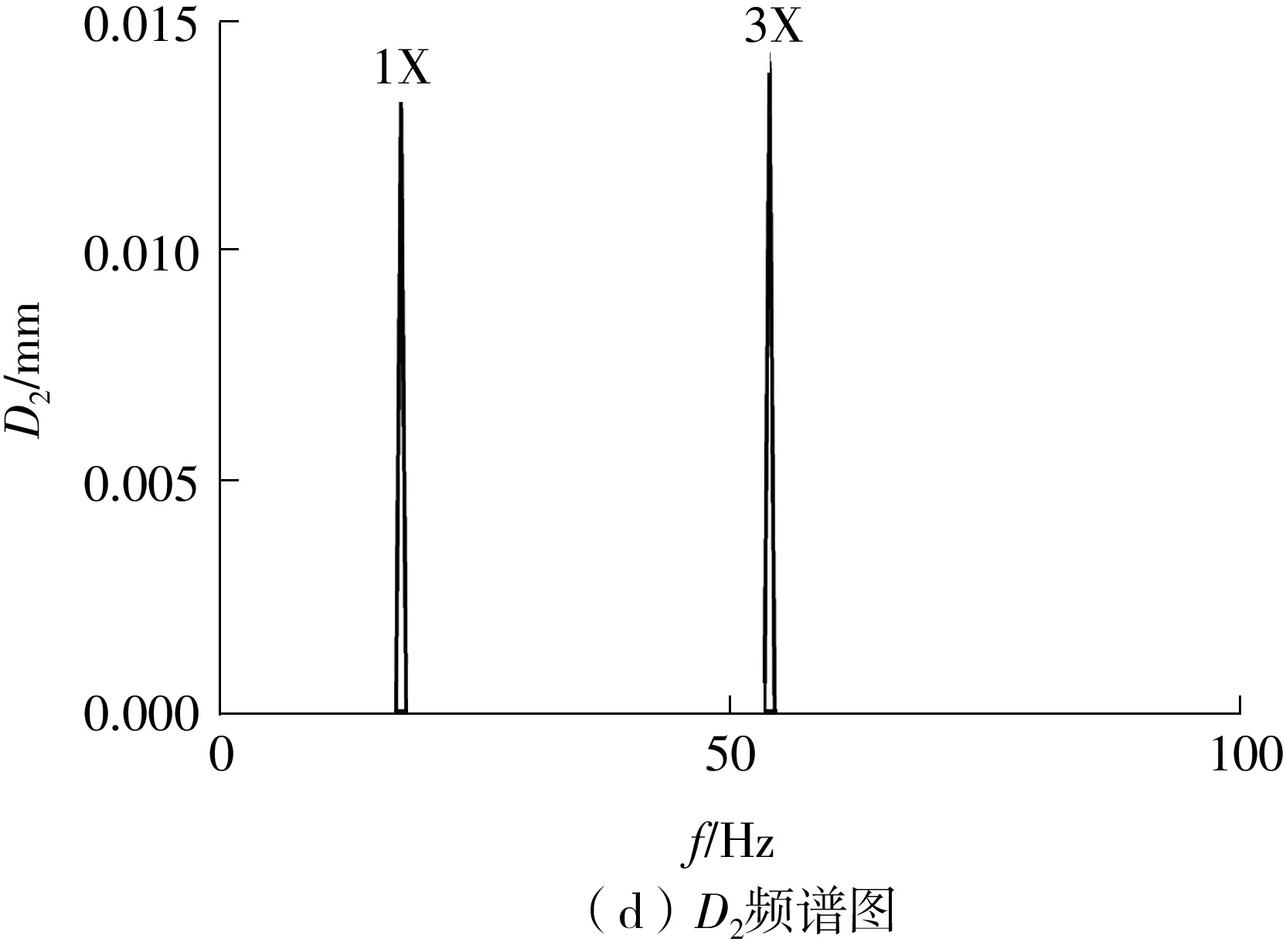
图9 提纯的信号Fig.9 Purified signals
图11(a)-11(e)所示为A端提纯的轴心轨迹。由图可知,升速过程中各稳定工况下的轴心轨迹都为规则的“花瓣形”。仔细观察发现,各个花瓣的中心与轴心轨迹中心的距离不一样,在整个升速过程中,左右两边的花瓣经历了部分分离—相交—部分分离—再相交—完全分离的过程,碰磨程度相应地经历了轻微—较严重—轻微—严重—更严重的变化过程。打开轴承端盖后发现,轴颈部位并未发现明显的碰磨痕迹(见图12),说明在该类油膜轴承的轴瓦摆动及油膜力作用下,转子的运行状态较复杂。

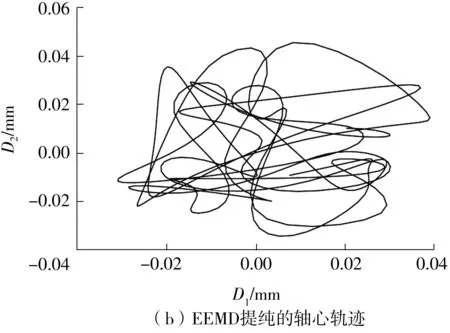
图10 轴心轨迹提纯效果对比Fig.10 Comparison of purified axis orbits
图11(f)-11(j)所示为采用B端信号提纯的轴心轨迹。由图可知:升速过程中各稳定工况下的轴心轨迹各不相同。其中,480 r/min转速下的轴心轨迹为“外8字”,说明此时存在较为严重的不对中故障,结合图8所示的主轴位置变化可发现,此时转子两端的轴心位置不在一条水平线上且存在较大的高度差;1 080 r/min转速下的轴心轨迹为“香蕉形”,说明随着A端轴颈位置的下降和B端轴颈位置的抬升,两端的高度差逐渐缩小,从而使得不对中程度有所缓解;2 280 r/min转速下的轴心轨迹为“蛇头形”,轴颈的运动状态较为复杂,此时A端的轴心位置下降到最低点,而自由端的位置依然在往上抬升,两者的位置差又开始增大;2 760 r/min和3 960 r/min转速下的轴心轨迹都为“香蕉形”,从图7中可以看出,在这两种工况下,两端的位置都是向上抬升的,所以不对中程度相对较轻。
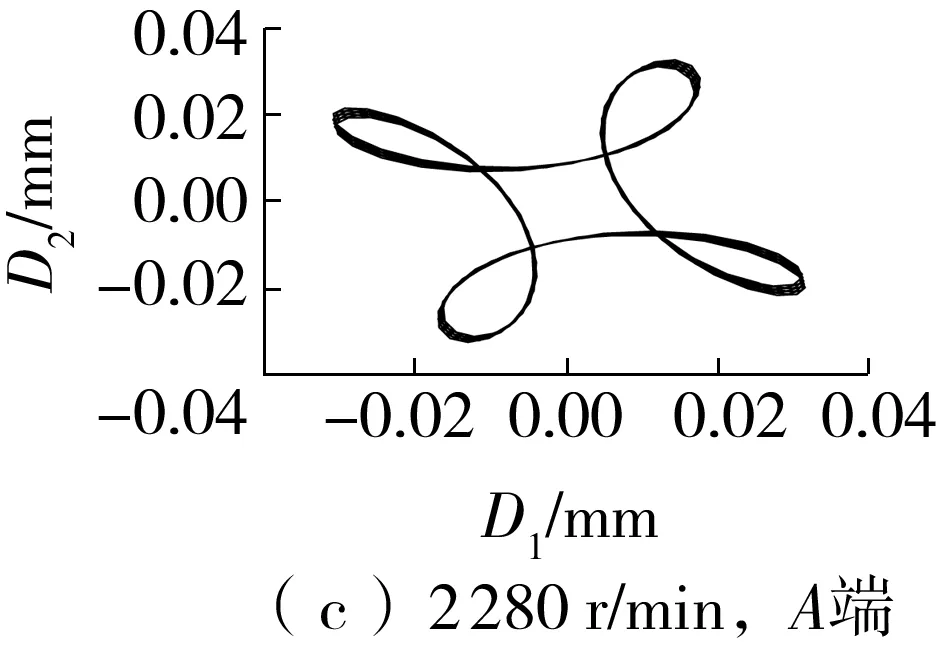

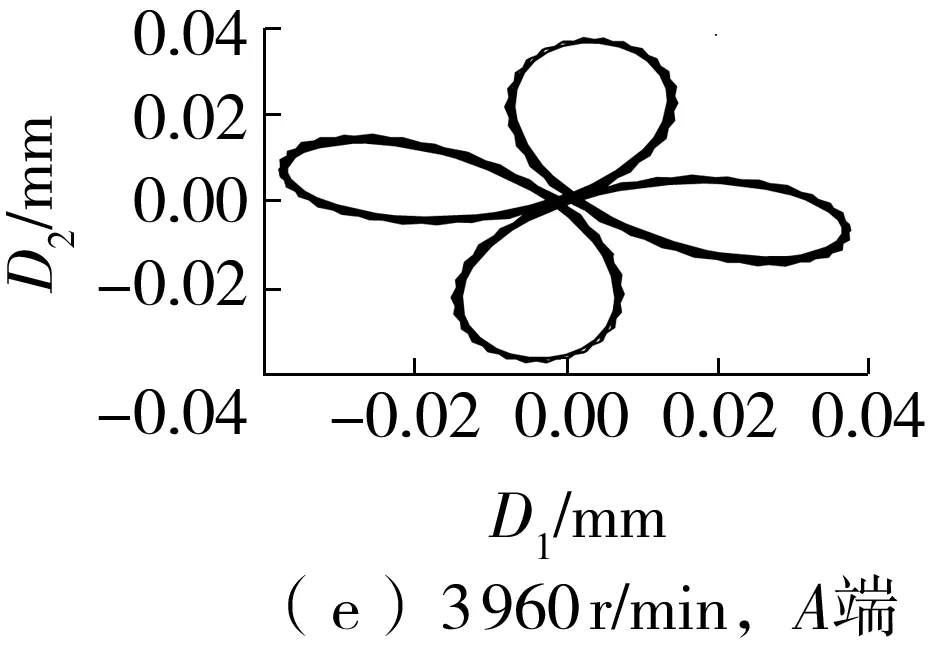
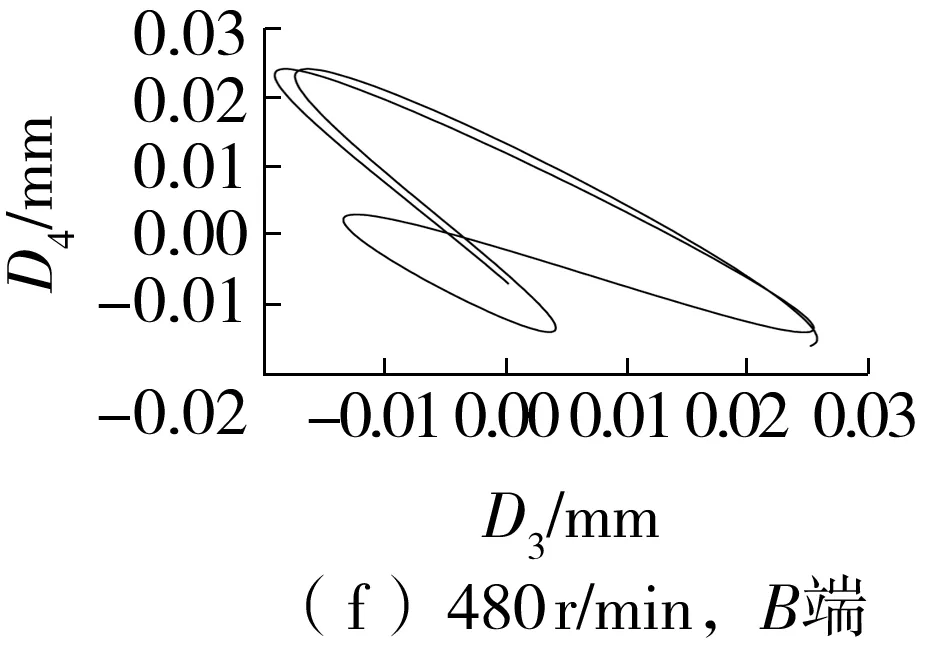
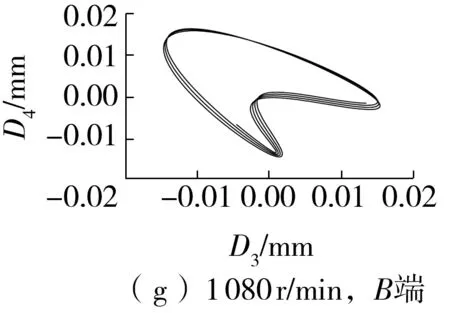
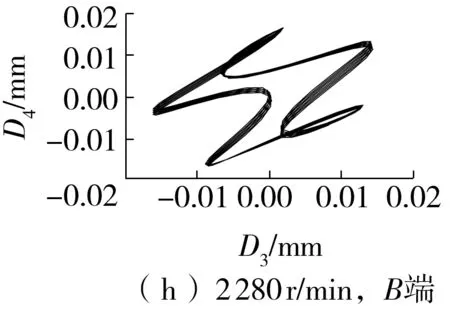
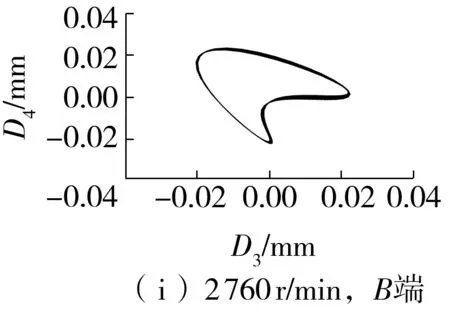
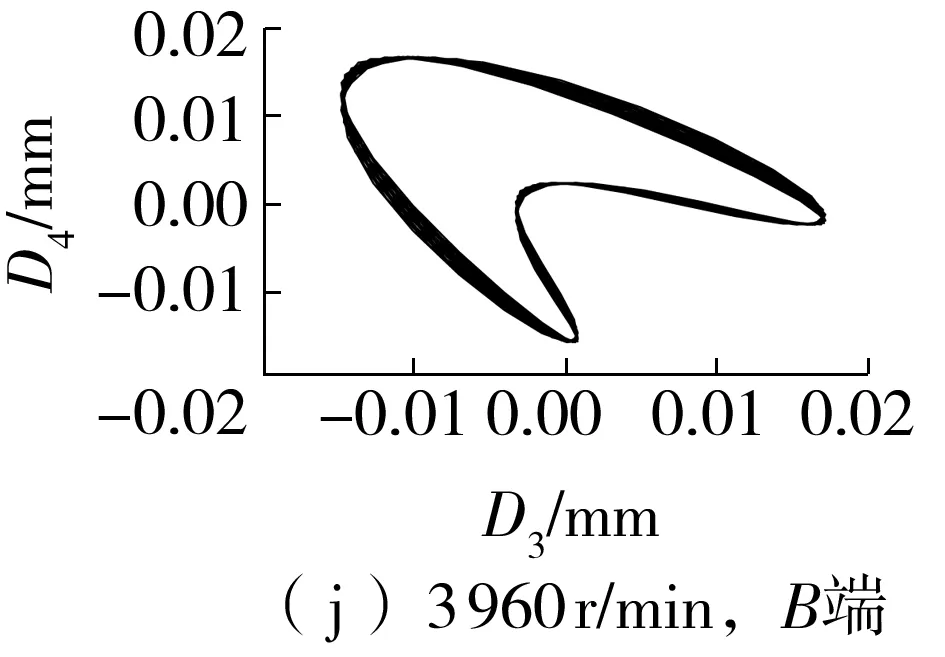
图11 提纯的轴心轨迹Fig.11 Purified axis trajectories

图12 轴颈实拍图Fig.12 Actual picture of shaft neck
4 结语
文中提出了一种基于稀疏分解理论的故障特征频率提取算法,该算法根据旋转机械振动信号的周期性特点来构建余弦字典,并采用匹配追踪算法求解稀疏系数。仿真案例证明,文中提出的稀疏算法是有效的,能够成功识别转子的多种故障类型。
文中还分析了主轴两端轴颈直流分量的变化规律及主轴位置的变化规律,指出两者都能表达主轴的位置;此外,通过两者可以定性分析转子的不对中程度。
将文中提出的稀疏算法应用于大型滑动轴承试验台转子的轴心轨迹提纯,提纯的轴心轨迹清晰、集中,根据轴心轨迹的形状可成功识别转子在不同转速工况下的故障类型。同时,对实验信号的分析结果验证了所提算法在轴心轨迹提纯方面的效果优于EEMD。
限于篇幅,文中仅研究了基于余弦字典的稀疏表征算法在滑动轴承转子故障特征提取中的应用,对于其他类型的字典及其他类型旋转机械的故障特征提取,还有待进一步研究。
