基于三维离散元的大直径钢圆筒下沉侧摩阻力

丁小彬 施钰 陈俊生†

(1.华南理工大学 土木与交通学院，广东 广州 510640;2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640)

大直径钢圆筒是一种新型的海洋、港口结构形式，具有无底、无盖、厚径比小的特点，属于空间体系薄壳结构[1- 2]。在港珠澳大桥东、西人工岛以及深中通道人工岛建设中，实现了大直径钢圆筒结构快速成岛的施工工艺[3]。大直径钢圆筒结构无需开挖便可直接插入软土地基中，具有地层适应性好、施工速度快的优点，在码头、围堰、护岸等工程中具有良好的应用前景。目前使用的钢圆筒最大直径达到了28 m[1- 2]，其长径比小于2，壁厚相对于直径的比小于0.001，因此这种结构的贯入阻力与以往的沉井、沉桩都不同。目前国内外对钢圆筒贯入机制的研究较少，因此有必要寻找一种合理的方法来计算并分析圆筒的贯入阻力，从而进一步优化钢圆筒的贯入过程。

大直径圆筒的贯入过程与沉桩十分相似，目前针对沉桩机理的研究较多，包括挤土效应、土塞效应以及桩基承载力等，国内外学者对此进行了大量的试验研究，包括现场试验[4- 8]和室内模型试验[9- 10]等。已有研究表明，土与结构的相互作用与土层属性、初始应力、桩径等有密切联系。对于开口桩，由于土塞效应，其贯入机理与闭口管桩存在明显不同[11]，相同深度处开口管桩的贯入阻力比闭口管桩小[12]。现有的试验研究主要揭示了沉桩过程的几个关键问题，包括桩-土界面剪切[13]、土塞效应和摩擦疲劳[14]等，而大直径钢圆筒因其筒壁薄且贯入深度与直径的比值较小，相比于开口管桩，结构与土的相互作用机理存在差异，故对其贯入机制有必要进行更深入的研究。

学者们在沉桩过程的理论分析方面也做了大量的研究，Vesic[15]最早提出将圆孔扩张理论应用于打桩过程的分析。Collins等[16]和Carter等[17]基于扩张理论，通过考虑不同的土体临界破坏模型，分析了土体的应力、应变和孔隙压力。也有一些学者利用扩张理论建立了侧摩阻力的计算模型。刘俊伟等[18]基于球孔扩张理论，考虑打桩过程中的侧阻力退化效应，提出了计算桩侧摩阻力的公式;李镜培等[19]分别采用球孔和柱孔扩张理论模拟了桩的应力状态，提出了饱和软土中沉桩阻力的计算方法。已有的沉桩理论研究成果对大直径钢圆筒结构贯入机理的分析具有一定的借鉴意义。

目前，由于试验仪器的局限性，难以通过模型试验或现场试验测得整个沉桩过程中的侧摩阻力分布，而理论方法又存在一定的简化和假设。因此，数值模拟的方法得到了研究者们的广泛关注。Wroth等[20]、Salgado等[21]、Randolph等[22]和Basu等[23]采用有限元法建立了桩土相互作用的数值计算模型，数值结果与实测数据表现出较好的一致性。然而，也有学者[24]指出，由于土体的颗粒属性及其特有的破坏模式，连续性假设可能存在潜在的缺陷。Cundall等[25]提出的离散元方法可以有效模拟介质开裂、分离等非连续现象，国内外学者也对贯入过程的离散元模拟进行了探索。早期的研究主要以二维模型为主。Huang等[26]最早利用二维圆盘模拟土颗粒，基于离散元理论进行了一系列标准贯入试验;Jiang等[27]基于二维离散元模型研究了斜向贯入试验的机理;Tu等[28]对采用离散元与有限元耦合模拟标准贯入过程的方法进行了探索。对于沉桩过程的模拟，叶建忠等[29]、Esposito等[30]、Nuo等[31]建立了闭口桩下沉的数值模型，詹永祥等[32]采用PFC2D模拟了开口管桩贯入过程中土塞的形成和演变过程，验证了离散元模拟的可行性。一些学者还建议通过考虑颗粒破碎进行建模[33- 35]，进一步为贯入过程的模拟提供了方法和思路，但多数二维模型以定性研究为主。近年来，一些学者开始建立沉桩过程的三维离散元模型，Butlanska等[36]、Zhang等[37]、Ciantia等[38]基于PFC3D研究贯入机理，得到的结果与试验现象基本相符，但也发现采用三维模型会导致计算效率的大幅降低。

目前，沉桩过程的离散元模拟主要为定性研究，且多为二维模型，而三维数值模型普遍存在计算效率低的问题。对于大直径钢圆筒，因其结构形式的特殊性，注定与沉桩过程存在差异。为定量分析大直径钢圆筒贯入过程中的侧摩阻力，并提高三维模型的计算效率，文中基于PFC3D，对大直径钢圆筒在砂土中的贯入过程进行数值模拟，通过对细观参数的校准，分别建立了基于离心机原理的缩尺模型和调整细观参数的足尺模型，并将模拟结果与理论计算结果、已有试验现象进行对比验证，研究钢圆筒下沉过程中内外侧摩阻力的分布和变化;同时，对两种模型生成方法进行比较，分析不同接触细观参数的影响，以期为后续研究提供参考。

1 模型建立

1.1 模型概况

港珠澳大桥西人工岛钢圆筒主要穿越的地层为中粗砂、粉土、粉质粘土。文中以砂土作为模型地基土，并假设圆筒匀速下沉。砂土的主要力学参数如图1所示。土体密度ρ=1.65 g/cm3，孔隙率n=0.41，内摩擦角φ=35°，压缩模量Es1- 2=25.62 MPa，粘聚力c=0 kPa。钢圆筒的主要参数为：直径d=22 m，壁厚t=18 mm，高度h=26 m，下沉深度20 m。

图1 钢圆筒的计算模型Fig.1 Calculation model of steel cylinder

1.2 接触模型

PFC3D是通过颗粒间的接触来模拟颗粒间的相互作用，每一个特定接触上的本构模型又可以分为线性接触模型、接触黏结模型、平行接触黏结模型等。线性模型适用于无粘性材料，有研究表明，该模型可以很好地模拟砂土[39]。文中采用线性接触模型，主要细观参数为：颗粒法向接触刚度kn、法向与切向刚度比kratio和摩擦系数u。

1.3 细观参数的校准

由于PFC采用的是接触细观参数，不能直接输入土体的宏观力学参数。细观接触参数与宏观力学参数之间没有具体的数学关系式，因此首先采用数值试验的方法确定颗粒试样的细观参数[40]。

如图2所示，基于PFC提供的函数集，采用半径放大法生成了试样密度为1 650 kg/m3、孔隙率为0.41、粒径为6～12 mm、颗粒数为2 236的数值试样，并分别进行三轴压缩和侧限压缩试验。

图2 压缩试验的数值模型Fig.2 Numerical model of compression test

(1)三轴压缩试验确定内摩擦角

为了减小边界效应并实现刚性加载，上、下加载板的接触刚度设置为颗粒刚度的10倍，而提供围压的墙体刚度选为颗粒刚度的0.1倍[40]。图3为分别在50、200和400 kPa的围压(σc)条件下加载得到的应力-应变曲线。以主应力差(σ1-σ3)的峰值为破坏点，若无峰值，则以应变达到15%时的主应力差为极限破坏点，并绘制莫尔强度包络线，得到试样的内摩擦角。

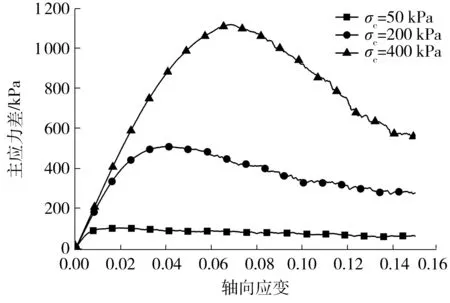
图3 数值试样的应力-应变曲线Fig.3 Stress-strain curves of numerical specimen

(2)侧限压缩试验确定压缩模量

压缩模量是指完全侧限条件下的垂直附加应力与相应应变增量之比。为了模拟完全侧限边界，将约束墙的刚度设置为颗粒刚度的10倍[40]。通过控制上、下加载墙体的相对位移来模拟受压过程，边界墙体设为静止状态，根据以下公式计算压缩模量：

Es1- 2=Δσ1- 2/Δε

(1)

式中:Δσ1- 2是垂直附加应力增量，范围为100～200 kPa;Δε是相应的应变增量。经过大量的试算，得到数值试样的内摩擦角为34.67°，压缩模量Es1- 2=25.62 MPa，与实际砂层基本一致。校准的颗粒细观参数如表1所示。

表1 颗粒的细观接触参数Table 1 Micro contact parameters of particle

1.4 缩尺模型的建立

1.4.1 模型地基的生成

如果以标定的颗粒大小来生成与实际等同的模型，会导致颗粒数量过于庞大，而现有计算机的计算能力有限，因此，可以采用离心试验的原理，缩小模型尺寸，通过增加重力加速度，使地层应力水平接近实际水平[41]。

建立PFC数值模型的方法主要有半径放大法、边界收缩法、重力沉积法、分层欠压法[42]等。半径放大法适用于制备具有指定孔隙比的试样，但颗粒重叠较多，初始应力大。重力沉积法与室内重力制样相似，但难以生成均匀的模型。边界收缩法适用于低孔隙率样品的制备，但很难保证整个模型的均匀。分层欠压法可以弥补上述方法的不足，故文中采用该方法来建立砂土地基模型，主要过程如下。

(1)分层。砂土地基试样共分5层生成，在每一个分层生成过程中，设置较大的初始孔隙比e0和摩擦系数，以便让试样稳定在很松散的状态[43]。固定模型箱底部和周围墙体单元，并将顶部边界墙体以1 m/s的速度向下移动，将每层指定生成的Ni个颗粒压密。

(2)欠压。为了使生成的地基土各层密实度均匀，并最终达到指定平均孔隙比(e)0.72，首先生成第1层，压缩至孔隙比e1比初始孔隙比e0大;再生成第2层，使第1层和第2层的平均孔隙比达到指定值e1+2;重复该步骤至最后一层n，每层生成的颗粒数Ni、层高及对应的平均孔隙比可参考Jiang等[42]所建议的方程确定。文中共分5层生成砂土地基试样，最终孔隙比e=0.72，每层的指定孔隙比为：e1=0.75，e1+2=0.743，e1+2+3=0.735，e1+2+3+4=0.728，e1+2+3+4+5=0.72。

采用分层欠压法生成地层模型(边界条件：长600 mm，宽600 mm，高450 mm)，共分为5层。模型颗粒生成后，施加重力，在100g的重力加速度下沉积、固结。删除高于设计表面的颗粒，并循环直至不平衡率小于0.000 1。最后生成颗粒数约为210 995、尺寸为600 mm×600 mm×400 mm的砂土地基模型，如图4所示。

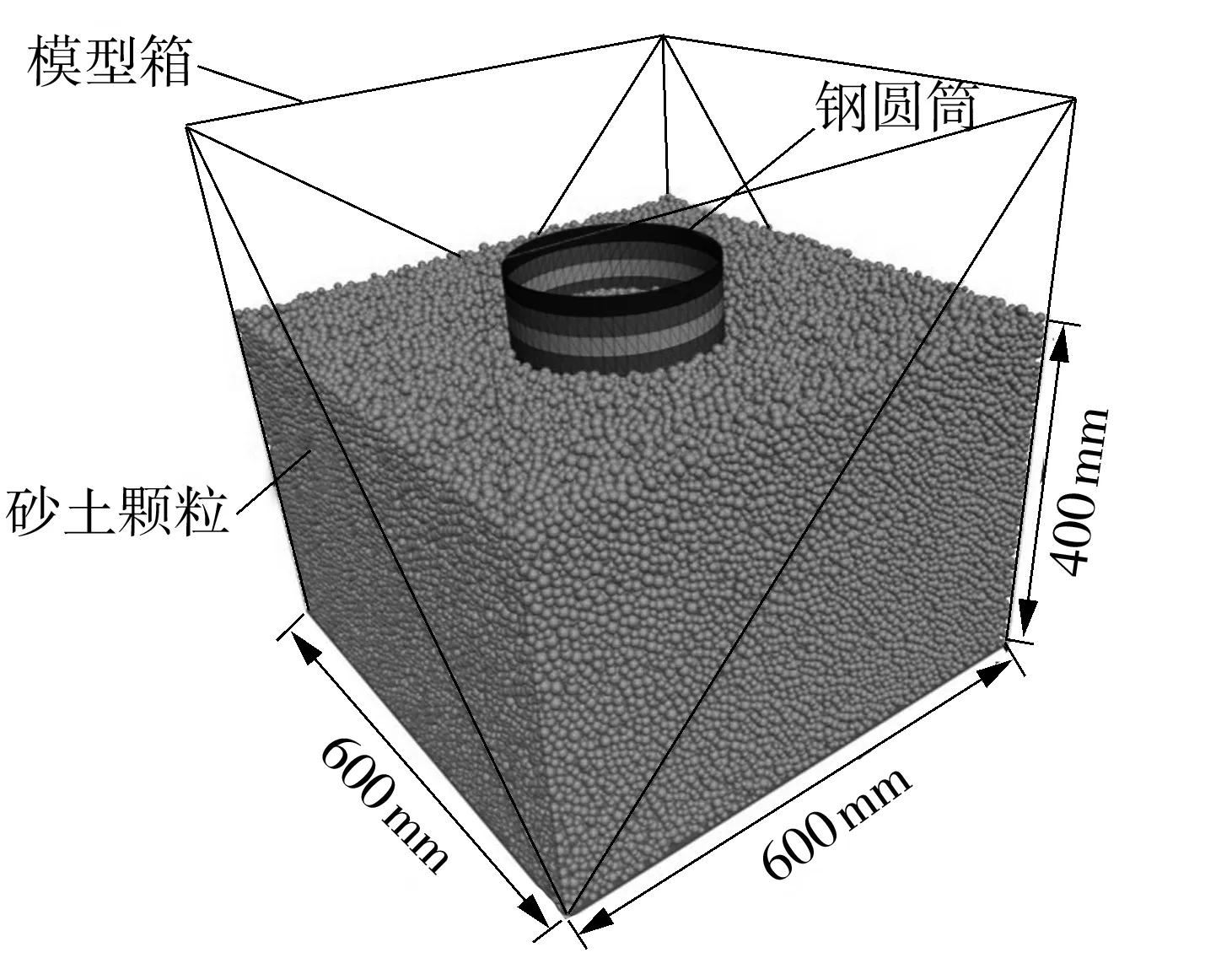
图4 钢圆筒贯入过程的数值模型

Fig.4 Numerical model of penetration process of steel cylinder

1.4.2 钢圆筒模型的生成

钢圆筒的实际直径是22 m，厚18 mm。厚径比很小，而且文中主要研究侧摩阻力，不考虑端部阻力，因此采用PFC墙体单元模拟圆筒。如图5所示，为得到不同高度处的侧摩阻力，将钢圆筒分成14段，从上到下前13段每段高度为20 mm，为忽略端阻力的影响，将最底部墙体的高度设为5 mm，以下部第2段墙体为计算侧摩阻力的起点，钢圆筒模型的主要参数设置如下：①由于钢圆筒的刚度远大于土体的刚度，因此将筒壁的刚度设置为109N/m;②有研究表明，钢-砂界面摩擦角为28°～29°[44]，故钢圆筒壁的摩擦系数tanδ=0.53;③为保证模型收敛及计算效率，通过试算，设圆筒的下沉速度为10 mm/s。详细参数见表2和3。

图5 钢圆筒的数值模型Fig.5 Numerical model of steel cylinder

表2 圆筒贯入模型的基本参数

Table 2 Basic parameters of penetration model of steel cylinder

模型颗粒数目贯入速度/(mm·s-1)模型尺寸/(mm×mm×mm)贯入深度/mm重力水平数值模拟21099510600×600×400200100g实际模型——60000×60000×40000200001g

表3 模型墙体的细观接触参数Table 3 Micro contact parameters of modal wall

1.4.3 量测手段

(1)检测应力场及模型孔隙分布

如图6所示，模型箱中设置半径为2 mm的测量球，填充整个模型，共计2 250个，用来检测圆筒贯入过程中筒体周围土层孔隙和应力场的变化。

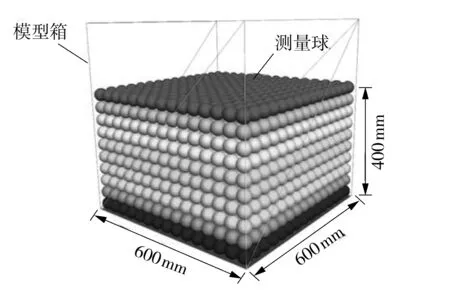
图6 测量球分布示意图Fig.6 Schematic diagram of measurement sphere distribution

(2)侧摩阻力的计算

基于PFC内置fish语言进行二次开发，通过遍历土体颗粒与各段钢圆筒的接触，分别计算颗粒与筒壁内外的垂直接触力分量，得到每段圆筒墙体的平均接触力，从而计算出圆筒筒壁内、外侧摩阻力。

1.5 足尺模型的建立

除了利用离心试验原理建立缩尺模型外，也有学者提出将颗粒粒径放大并调整接触属性建立足尺模型[45]。由于标定的颗粒尺寸非常小，如果以该粒径建立足尺模型，那么生成的颗粒数会过多。而若仅将颗粒尺寸放大，虽然可以提高计算效率，但尺寸效应会导致模拟结果的失真[46]。为保证放大粒径后的试样与原标定试样的宏观性质基本一致，通过几何相似比调整接触参数如下[45]：

(2)

式中，kn0和kn1分别为初始标定颗粒和粒径放大颗粒的法向接触刚度，ks0和ks1分别为初始标定颗粒和粒径放大颗粒的切向接触刚度，A0和A1为相应的接触面积，L0和L1为接触长度，Ec0和Ec1为接触模量，u0和u1为接触摩擦系数，CL为几何相似比。如图7所示，为了确保放大后的颗粒与校准的颗粒试样具有相同的应力-应变关系，其接触模量应相同。

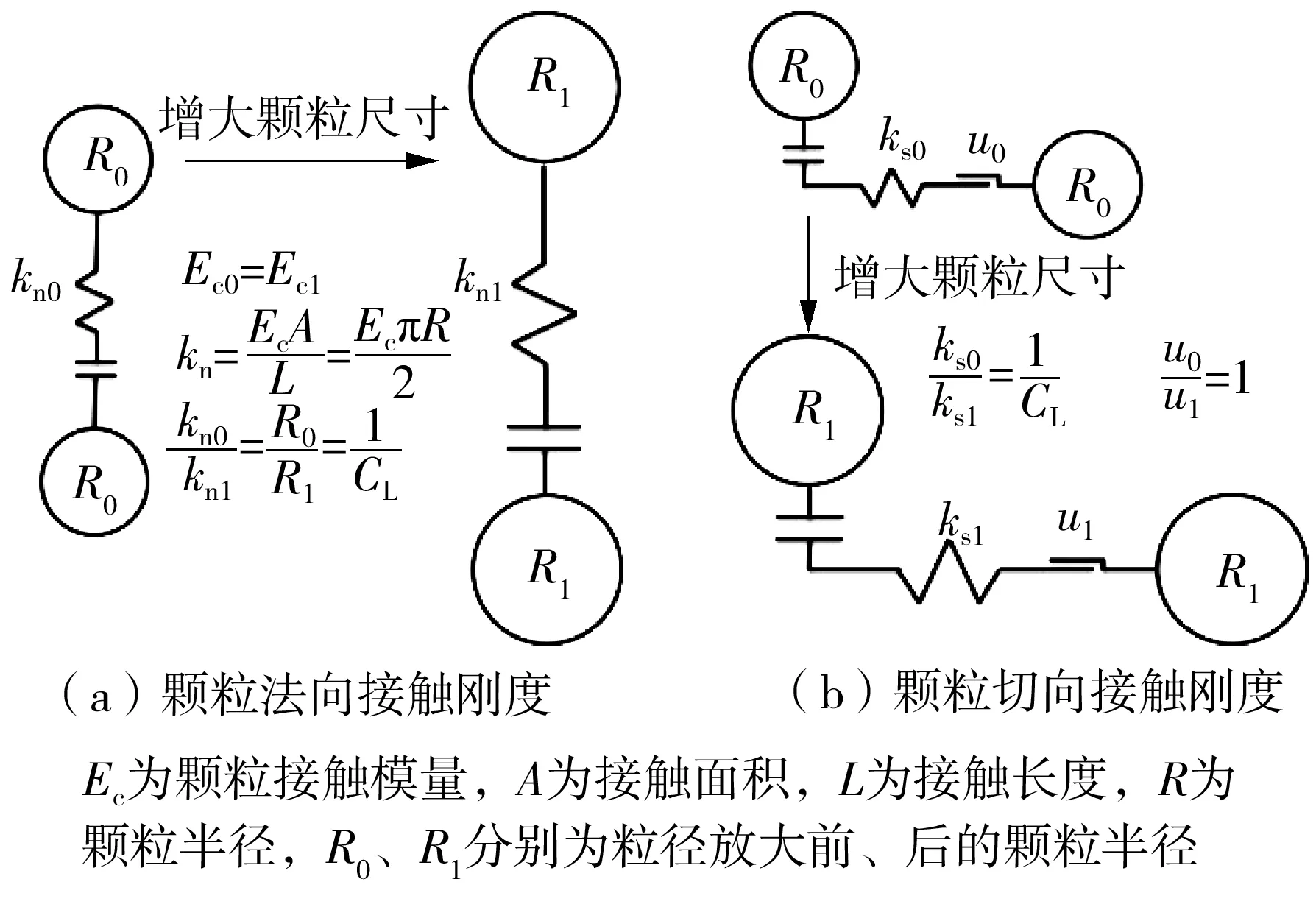
图7 颗粒缩放理论接触参数调整原则示意图

Fig.7 Schematic diagram of contact parameter adjustment in particle upscale theory

为了验证该相似准则在三维模型中的适用性，首先进行了一系列数值试验。具体方法为：在上述标定试验的基础上，建立两组不同粒径的数值试样，其中一组随颗粒粒径调整其接触参数，而对照组的接触参数保持不变，仅改变颗粒粒径。随后分别进行三轴压缩试验和侧限压缩试验，得到围压为50 kPa时的压缩模量和峰值应力，见图8。

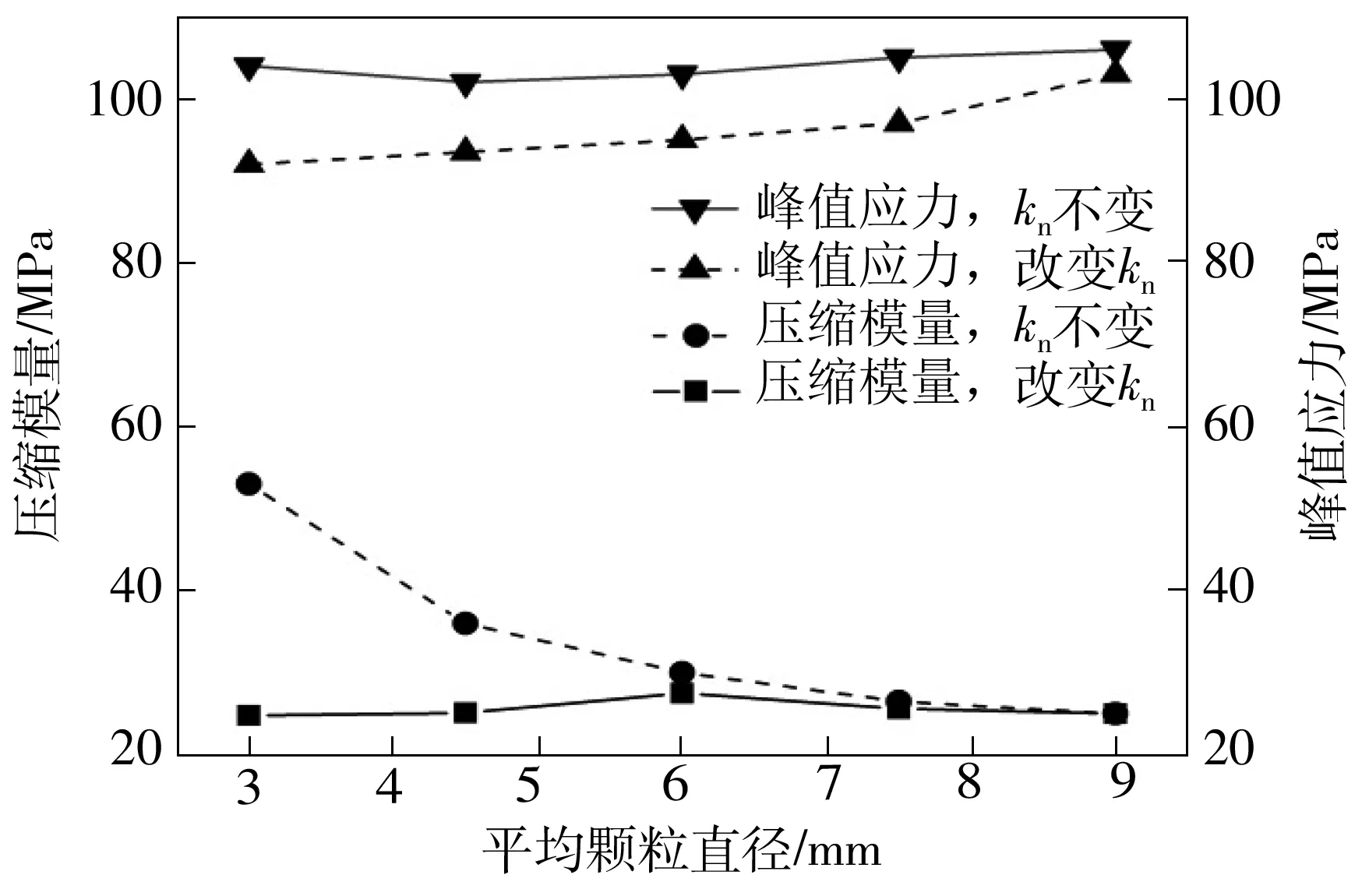
图8 两种模型压缩试验结果的比较Fig.8 Comparison of test results of two compression models

由图8可知，对于三维PFC模型，随粒径改变而调整接触参数的试样组，其压缩模量和峰值应力基本保持不变，相比之下，不改变接触属性的试样组受粒径变化的影响较大。这表明，通过适当调整接触参数，可以使得不同粒径的数值模型具有相近的宏观力学性质。

因此，基于上述接触参数调整原则，建立钢圆筒贯入过程的足尺模型，详细建模方法与缩尺模型类似，具体接触参数如表4所示。

表4 缩尺模型与足尺模型参数对比Table 4 Comparison of parameters between scaled model and full-scale model

由表4可知，缩尺模型的时间步长为5×10-7s，而足尺模型的时间步长为4×10-5s，相差了近百倍，相应的缩尺模型的运行时间为115 h，而足尺模型的运行时间仅为23 h，明显提高了计算效率。

2 结果分析

2.1 侧摩阻力理论公式

为验证数值模拟结果，首先对已有理论研究的结果进行分析。在圆筒贯入过程中，筒壁受到的侧摩阻力为滑动摩擦力。根据库仑摩擦定律，侧摩阻力f为

(3)

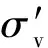
工程上通常采用与现场静力触探结果相关的经验公式来估算桩侧摩阻力。表5列出了计算桩侧摩阻力的一些代表性公式。这些经验公式主要适用于计算桩的承载力，即桩周土固结后桩的极限侧摩阻力，不同于文中所模拟的圆筒贯入过程中的动摩擦力。对于滑动摩擦，一些研究者也提出了基于圆孔扩张理论的计算公式。如表5所示，文中选用了一些具有代表性的理论公式与数值模拟结果进行对比。主要计算参数为：土体密度ρ=1.65 g/cm3，粘聚力c=0 kPa，内摩擦角φ=35°，压缩模量Es1- 2=25.62 MPa，剪切模量G=30 MPa，钢圆筒直径d=22 m，壁厚t=18 mm，贯入深度h=20 m。

表5 桩侧摩阻力的计算公式1)Table 5 Calculation formula of pile side friction

1)部分符号的含义参见对应的文献，篇幅所限，文中不一一列出。

2.2 数值结果分析

2.2.1 缩尺模型侧摩阻力计算结果验证及分析

图9为采用缩尺模型时，贯入过程中钢圆筒侧摩阻力的数值和理论计算结果，该计算结果为圆筒侧壁在贯入深度范围内分布的单位侧摩阻力。由图可知，数值计算得到的单位外侧摩阻力分布曲线介于按K0和Kp计算得到的分布曲线之间。圆筒顶部的单位侧摩阻力很小，中部的单位侧摩阻力随着深度的增加而逐渐增大，而底部单位侧摩阻力的增加程度最为显著，数值模拟得到的单位侧摩阻力分布与按圆孔扩张理论计算的结果基本接近。

图10为钢圆筒单位侧摩阻力的分布曲线。由图可知：单位总侧摩阻力的变化趋势与单位内侧摩阻力基本相同。单位内侧摩阻力约为单位总侧摩阻力的一半，两者的差值随贯入深度的增加而增大;而且单位内侧摩阻力在筒体内壁均有分布，贯入过程中没有土塞效应。

图10 单位侧摩阻力的分布Fig.10 Distribution of unit side friction

图11和12为钢圆筒贯入深度为200 mm时接触力链的分布。接触力链的粗细表示接触力的大小，力链越粗则接触力越大。由图可知，在圆筒底部约0.2倍贯入深度范围内，接触力链较粗且分布密集，圆筒底部附近的颗粒受到较大的挤压作用，使得该处的单位侧摩阻力较大，且分布接近竖直，这与文献[50]中的沉桩端部单位侧摩阻力理论及实测结果基本接近，接触力链沿圆筒深度方向自上而下由疏到密，呈非线性变化，而颗粒受到挤压的区域主要集中在圆筒端部，当圆筒贯入至更深处后，原本受挤压的颗粒受到明显的扰动，因此单位侧摩阻力分布曲线表现出明显的起伏。而在钢圆筒内侧，一些较粗的力链相互连接形成接触力链网，使土颗粒的接触力重新调整，在接触力链网中，颗粒所受的接触力较小，而圆筒外侧颗粒受到明显的侧向挤压作用，没有形成明显的力链网。

图11 接触力链的纵断面Fig.11 Longitudinal section of contact force chains

图12 接触力链的横断面Fig.12 Cross section of contact force chains

图13和14为钢圆筒贯入深度分别为60、120和200 mm时的单位总侧摩阻力和单位内侧摩阻力分布曲线。结果表明，在同一水平位置，随着钢圆筒的贯入，单位总侧摩阻力和单位内侧摩阻力均有所减小，即内、外侧摩阻力均具有摩擦疲劳效应。

2.2.2 缩尺模型土层水平应力分析

图15(a)-15(d)分别为缩尺模型中，钢圆筒贯入深度分别为50、100、150和200 mm时，土体在距离20、60、100、140和180 mm范围内的

图13 单位总侧摩阻力的分布Fig.13 Distribution of unit total sidefriction

图14 单位内侧摩阻力的分布Fig.14 Distribution of unit inside friction

水平应力的分布。由图可知：钢圆筒下沉过程中引起的土层水平应力的变化主要分布在筒壁附近60 mm的范围内，而当距离超过100 mm时，其影响较小;靠近圆筒底部的土体水平应力明显增大，最大应力可达初始应力的3～5倍;与初始水平应力相比，圆筒顶端附近土的水平应力有所降低。数值模型的应力分布与文献[9]中打桩试验得到的结果基本一致，在钢圆筒贯入过程中，由于筒体底部附近的土颗粒受到明显的挤压作用，土体的水平应力明显增大，而靠近顶端附近的土颗粒因钢圆筒的循环剪切作用受到明显的扰动，导致水平应力减小。

2.2.3 两种建模方法的对比

图16所示为缩尺模型(相似比为1∶100)和足尺模型(相似比为1∶1)初始模型土层生成时的孔隙率和应力分布。由图可知，采用两种方法生成的模型初始应力水平和孔隙率基本相同，但是模型生成的时间存在明显差距。由表4可知，缩尺模型的时间步长远小于足尺模型，足尺模型的计算效率更高。

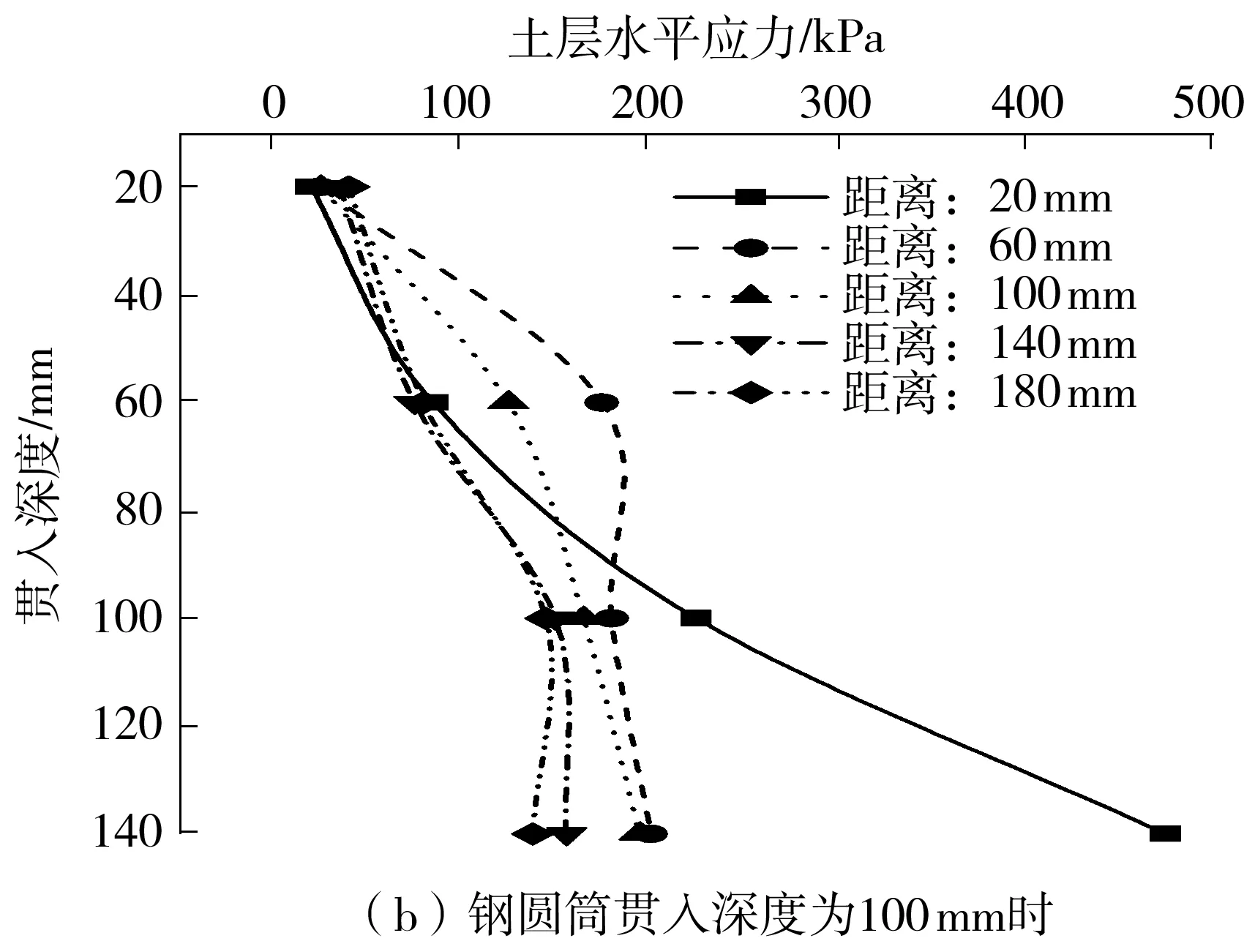
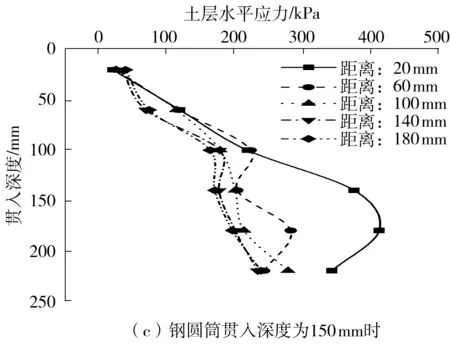
图15 不同钢圆筒贯入深度时的土层水平应力分布曲线

Fig.15 Horizontal stress distribution curves of soil at different penetration depths of steel cylinder

图17所示为采用两种方法得到的圆筒贯入过程中侧摩阻力的分布情况，其中采用缩尺模型的数值结果按1∶100的比例放大。由图可知，足尺模型的侧摩阻力大小、分布与缩尺模型的基本一致，说明调整接触参数的足尺模型同样适用。

图17 两种模型的单位侧摩阻力分布比较Fig.17 Distribution of unit side friction between two models

综上，两种模型生成方法得到的结果具有较好的一致性，但是足尺模型的计算效率较高，这与保证模型收敛的稳定时间步长有关，足尺模型的时间步长较大，计算效率也较高。因此，以足尺模型展开后续的参数分析。

2.3 细观参数影响性分析

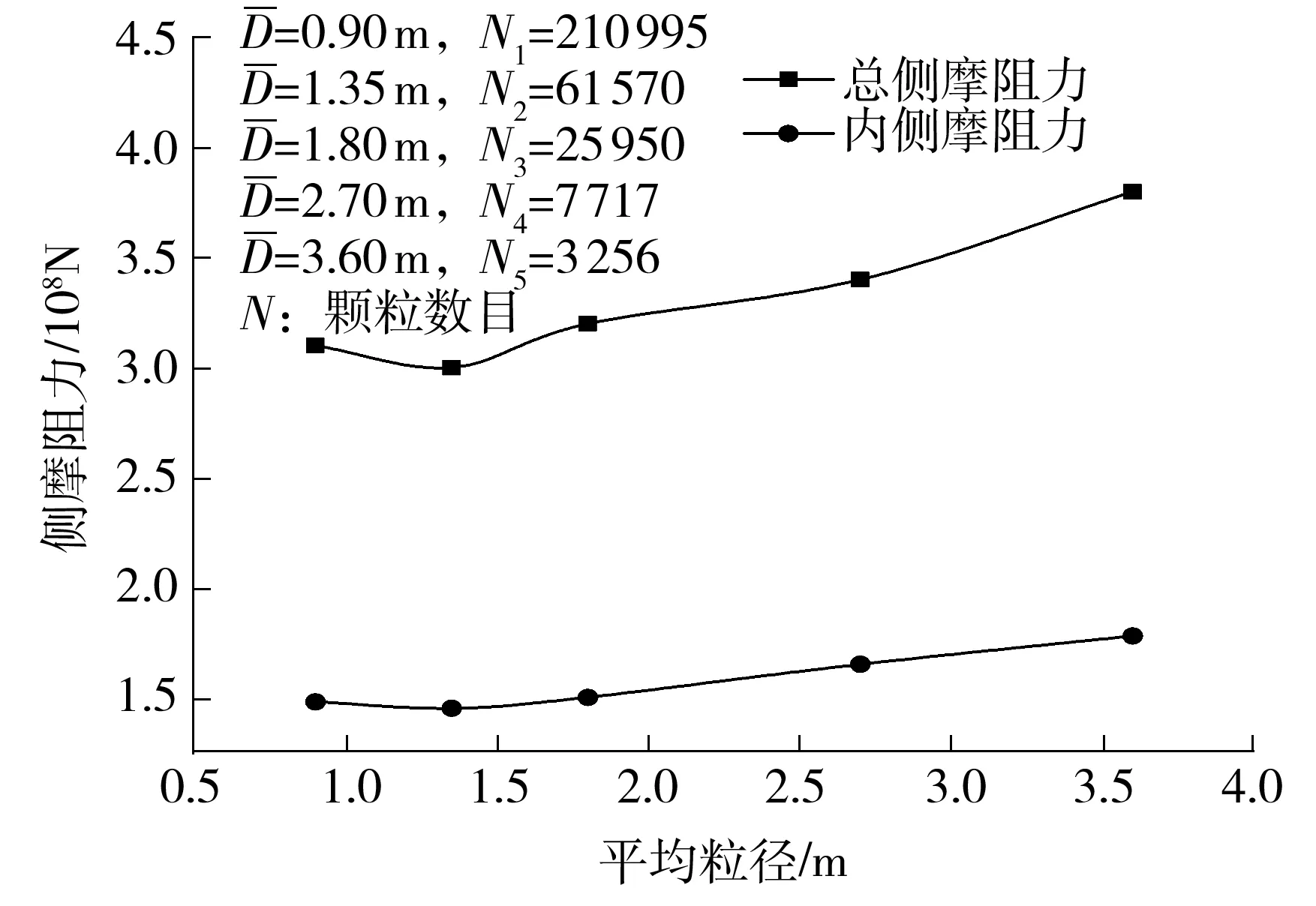
图18 平均粒径对侧摩阻力的影响Fig.18 Influence of average particle size on side friction

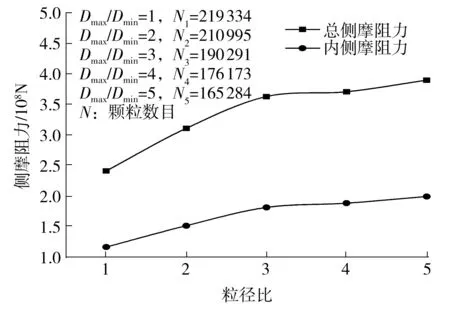
图19 粒径比对侧摩阻力的影响Fig.19 Influence of particle size ratio on side friction

2.3.2 贯入速度的影响

图20所示为基于足尺模型得到的不同贯入速度下的侧摩阻力计算结果。当钢筒的贯入速度较小时，对应的侧摩阻力的大小基本相同。但当贯入速度过快(大于10 m/s)时，侧摩阻力明显增大，并且模型中有颗粒飞出，此时圆筒的贯入过程与冲击相似。因此，为了兼顾数值模型的准确性和计算效率，通过大量试算，对于足尺模型，将钢圆筒的贯入速度设定为1 m/s。

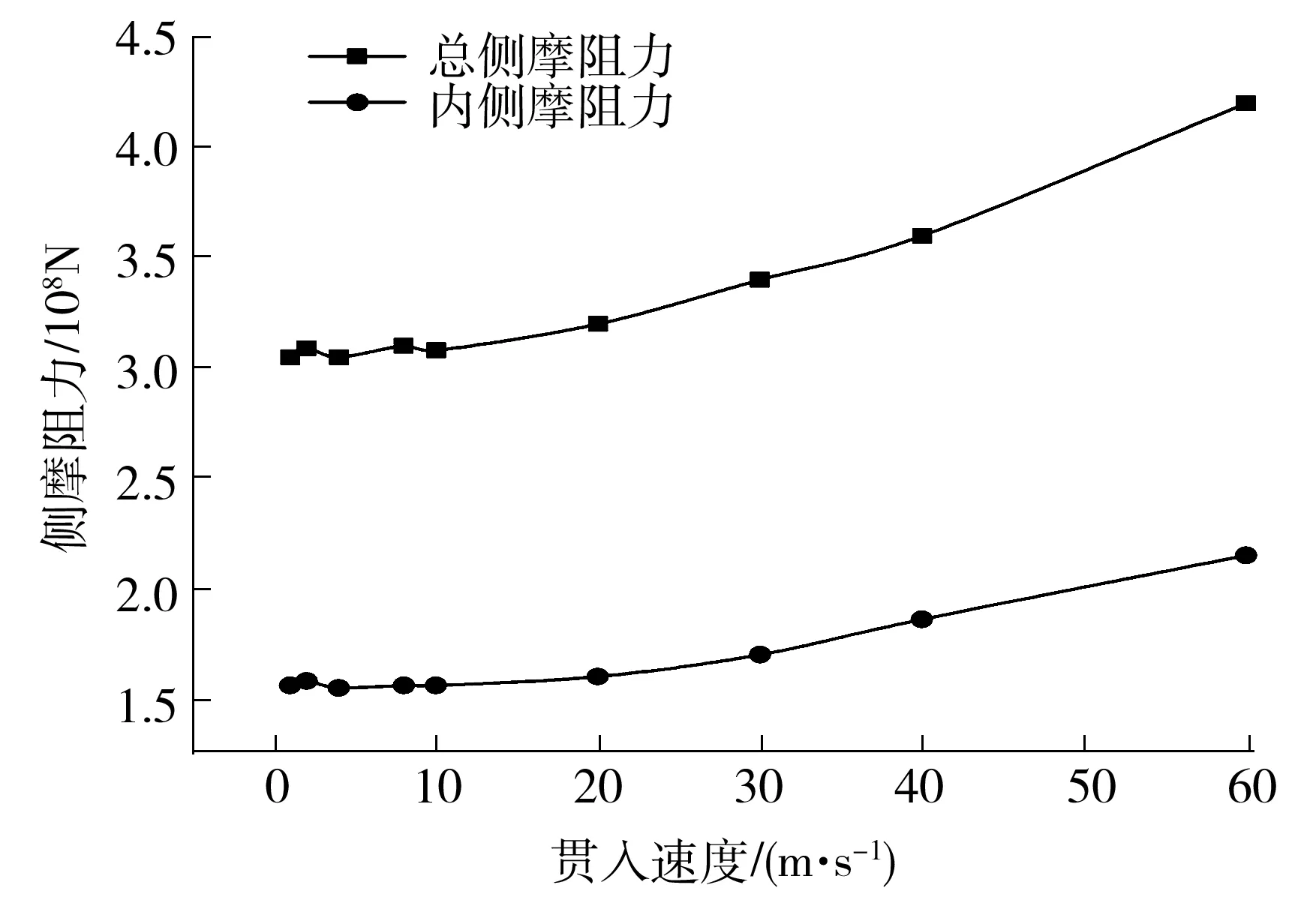
图20 贯入速度对侧摩阻力的影响Fig.20 Effect of penetration velocity on side friction

2.3.3 颗粒接触刚度和摩擦系数的影响

图21(a)和图21(b)分别示出了颗粒接触刚度和摩擦系数对钢圆筒侧摩阻力的影响，图中侧摩阻力的大小为单位侧摩阻力之和。结果表明：随着颗粒接触刚度的增大，圆筒贯入过程中的内、外侧摩阻力呈增大趋势。由于数值试样的压缩模量与颗粒接触刚度正相关，因此当接触刚度较大时，土体难以被压缩，贯入阻力也随之增大;另一方面，随着颗粒摩擦系数的增大，圆筒的侧摩阻力逐渐增大，但达到一定值后，下沉阻力的增长趋势变缓。相关研究[51]指出，颗粒摩擦系数是影响砂土试样内摩擦角的主要因素。摩擦系数越大，内摩擦角越大，但达到一定水平后内摩擦角不会继续增大，这与离散元所采用的圆形颗粒这一颗粒形式的内在缺陷有关——当摩擦系数较小时，颗粒相对滑动是颗粒运动的主要形式，剪切强度随着摩擦系数增大而增大;而当摩擦系数较大时，颗粒间相对滚动较多，剪切强度与摩擦系数表现出非线性的关系[52]。

2.3.4 墙体接触刚度与摩擦系数的影响

图21(c)和21(d)分别示出了钢圆筒接触刚度及摩擦系数对侧摩阻力的影响。如图21(c)所示，钢圆筒接触刚度对贯入阻力的影响不大，这是由于圆筒接触刚度远大于土体接触刚度。对于刚度远大于土的圆筒或桩，当接触面摩擦性质相近时，下沉过程中的侧摩阻力相差较小。图21(d)中，钢圆筒的侧摩阻力随圆筒摩擦系数的增大而明显增大，说明筒壁粗糙度是影响侧摩阻力的重要因素，但当摩擦系数增大到一定程度时，侧摩阻力的增大趋势明显变缓。这是由于墙体摩擦系数较小时圆筒对颗粒的竖向扰动较小，随着摩擦系数的增大，侧摩阻力随着墙体摩擦系数线性增大，而当墙体摩擦系数较大，尤其是接近颗粒间摩擦系数时，筒壁对颗粒的竖向扰动明显增强，此时存在较多颗粒与颗粒间的剪切滑动，使得侧摩阻力与墙体摩擦系数不再呈线性关系，而土与结构间的摩擦角一般小于内摩擦角，导致侧摩阻力的增大趋势变缓。

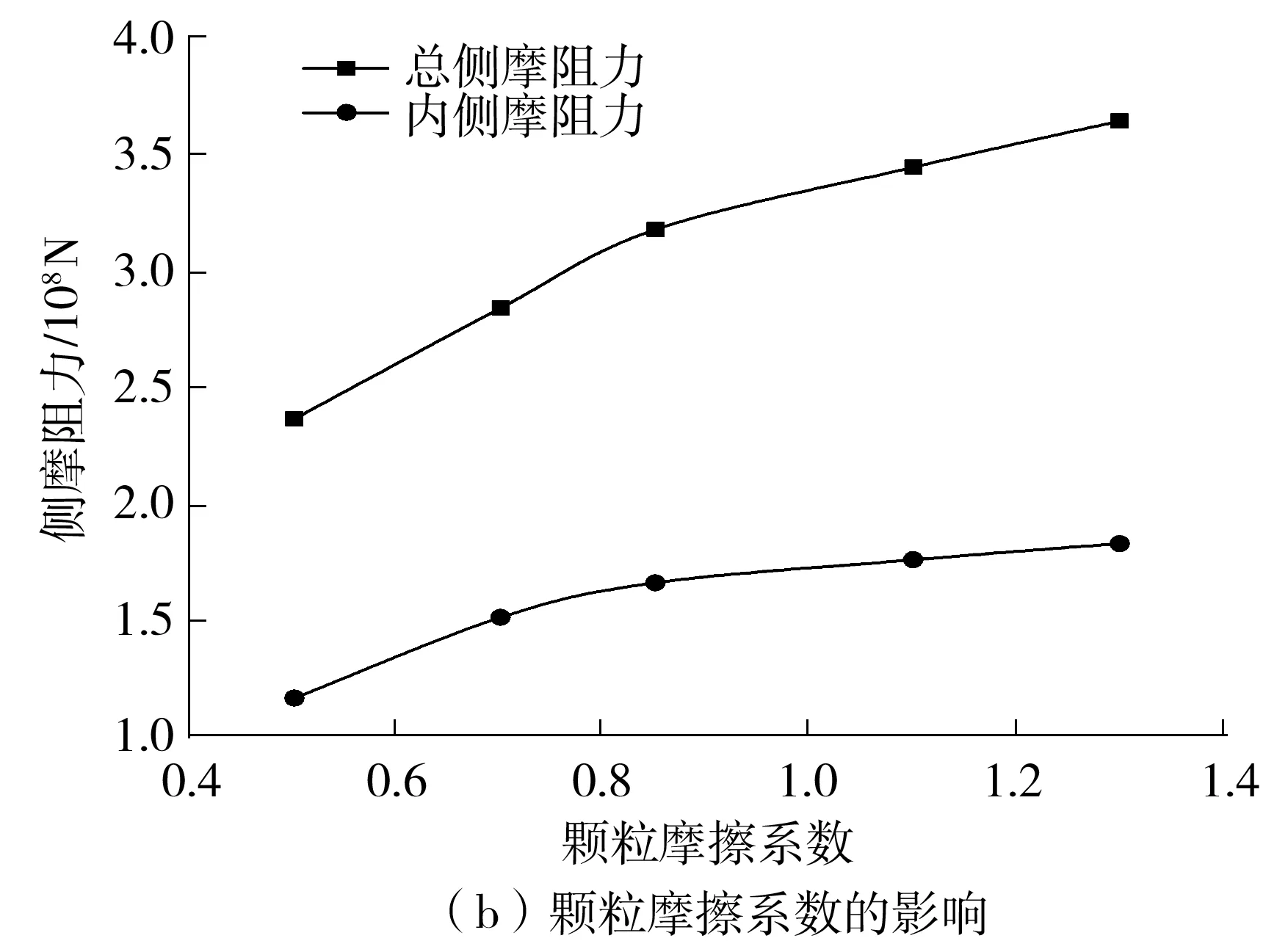
图21 细观接触参数对侧摩阻力的影响Fig.21 Effect of micro contact parameters on side friction

3 结论

文中基于颗粒流理论对砂土中大直径钢圆筒的贯入过程进行了三维数值模拟分析，所得主要结论如下：

(1)大直径钢圆筒在贯入过程中，筒体内外土层高度差很小，不会产生土塞效应;内侧摩阻力约为总侧摩阻力的一半，且内侧与总侧摩阻力的差值随贯入深度的增加不断增大，侧摩阻力存在摩擦疲劳效应;土体应力的变化与离筒壁的水平距离有关，土体中的高应力区主要集中于筒底，随着钢圆筒的下沉，高应力区也向下转移，而筒身的应力与周围土体的初始应力接近。

(2)通过细观的校准，基于离心机原理的缩尺模型和调整细观参数的足尺模型得到的结果相近，均具有一定的适用性。但是足尺模型保证模型收敛的时间步长较大，计算效率更高，更适合对实际工程问题的模拟。

(3)细观参数对模型宏观反应的影响如下：①合理的贯入速度及颗粒尺寸分布，是保证模型收敛和稳定的基础，应通过逐步试算确定;②钢圆筒贯入阻力与颗粒间的接触刚度呈正相关，而圆筒的刚度对贯入阻力的影响较小;③与颗粒摩擦系数相比，圆筒与土体颗粒间的摩擦系数对下沉阻力的影响更为明显。