污染土壤高压旋喷修复药剂迁移透明土试验及数值模拟
2020-06-17武亚军韩亚东陈天慧
武亚军,韩亚东,唐 欣,陈 敏,陈天慧
(1. 上海大学土木工程系,上海200444;2. 上海市岩土工程检测中心,上海200444)
土壤是生态系统的重要组成部分,是人类生存和发展的基本自然资源。随着经济高速发展,大量的生活垃圾、工业废物未经处理就直接排放,在自然因素的影响下转移至土壤环境中[1]。随着时间的推移,土壤污染物大量富集在农作物内,通过食物链进入人体,严重危害人类健康。近年来,中国工业化进程中土壤污染问题日益突出,国内的污染场地数量增多,造成了巨大的环境与安全危害[2]。在2014 年公布的《全国土壤污染状况调查公报》[3]中显示,全国土壤污染总超标率达到16.1%。因此,对污染土壤进行修复亟需提上日程。
依据场地污染类型、修复药剂的不同,注药方式也各不相同,药剂注入与均匀化控制技术是原位修复的关键,常用的药剂注入技术有直压式注射法、注射井法和高压旋喷注射法等[4]。高压旋喷注药法是近年来应用于污染土壤修复的一种原位注药方式,适用于渗透性较小的粘性土壤[5],目前在上海地区已经被应用于一些污染土壤场地的原位修复工程中,并突显出强大的生命力。高压旋喷注药法是将带有特殊喷嘴的注浆管,置入预先设定的深度,以高压射流切割土体,同时旋转提升,土体被切割成泥饼状(图1),药剂存在于相邻泥饼之间的缝隙中,然后向泥饼内扩散。修复效果与药剂的迁移和分布密切相关,只有药剂满足一定浓度的区域才能达到最佳修复效果,药剂浓度过高或过低都无法达到预期修复目的。目前对于修复药剂在高压旋喷所形成的泥饼内扩散规律的研究鲜有报道,工程实践中急需相关指导性的研究成果。

图1 高压旋喷注药后的泥饼土样Fig.1 Mud cake soil sample after high pressure rotary spray
目前,针对修复药剂在污染土壤中迁移的研究成果较少,在迁移扩散过程中修复药剂可以看作是一种溶质,探究修复药剂在泥饼中的迁移过程类似于探究溶质在多孔介质中的迁移,因此,可以借鉴污染物等溶质的研究方法对修复药剂的迁移扩散规律开展研究。国内外学者采用试验和数值模拟等手段对污染物的迁移特性进行了大量研究。在试验方面:郑顺安等[6]通过土柱模拟试验并应用Hydrus-1D软件研究了我国七种典型农田土壤中铜的吸附解吸、迁移积累等特性。Patrick 等[7]研究认为扩散和固结引起的对流作用对溶质迁移有重要影响。章明奎等[8]用室内模拟的方法研究了两种抗生素在7 个典型农业土壤中的吸附和迁移行为,研究表明这两种抗生素在粘质农业土壤剖面中的迁移能力较弱,砂质土壤中较易。上官宇先、王亚平[9]通过土柱淋滤试验研究了不同土壤质地对多种重金属的吸附特性及其在土壤中的运移特性。李小孟等[10]通过土柱吸附试验研究表明土壤中溶解态有机质有利于重金属离子向下迁移。
在数值模拟方面:林青等[11]用Freundlich 方程对镉在粉壤中运移过程进行了数值模拟,研究了不同土壤对镉运移的阻滞能力。许增光等[12]针对缓慢注氧修复技术开发了相应程序,结果表明注氧井离污染源越近能达到更好的修复效果。赵栗笠等[13]应用Visual Modflow 软件对存在渗油的加油站进行场地模拟分析,建立了甲基叔丁基醚(Methyl tert-butyl ether,MTBE)的三维羽状污染模型,分析污染源强度并预测其对周围区域产生的影响。
从以上研究可以看出,室内试验中的土样通常采用常规土壤,在取土检测过程中不仅会对土壤产生扰动影响分析结果;而且还无法连续观测土体内部溶质迁移的全过程。为解决这一问题,近年来透明土试验技术被引入到岩土工程中来。孔纲强等[14]应用熔融石英砂、混合油制成透明土试样,进行电渗模型试验,研究得到渗透率与福建标准砂的渗透率接近。Iskander、Liu[15]采用无定形二氧化硅和与其折射率相匹配的孔隙液体制配出透明土,发现其岩土工程性质与黏土相似。宫全美等[16]应用15 号白油和正十二烷混合溶液与无定型硅粉组成透明土进行了常规固结压缩试验,验证了其模拟粘土的可行性。White 等[17]将透明土与粒子图像测速法(Particle image velocimetry,PIV)技术相结合,实现了可视化地观测土体内部的变形。隋旺华等[18]应用透明土试验技术揭示了水砂混合物在岩体裂缝和破碎岩体中的运移规律。
本文将透明土材料应用于污染土壤旋喷修复药剂的扩散研究,进行了两方面的工作,首先使用无定型硅粉和白油配置成的透明土试样进行了修复药剂迁移的室内试验,通过外接摄像设备记录下土壤内部修复药剂迁移的全过程,结合数字图像处理技术研究了泥饼中修复药剂的迁移规律;然后采用数值模拟手段考虑了土体性质、泥饼高度、水力边界、溶质扩散系数和药剂初始浓度分布形式等因素对药剂迁移过程的影响。
1 透明土药剂迁移试验
1.1 试验方案
为了模拟上海地区的粘性土,采用无定型二氧化硅、2号白油和正十二烷制配透明土。
制配好透明土试样并进行了大量土工试验,通过对比透明土与上海粘性土在固结、渗透等基本性质的相似性,表明如表1 所示的透明土试样可模拟渗透系数为1.5×10-7cm·s-1的土体,能够用来模拟修复药剂的迁移特性研究。

表1 透明土组成成分Tab.1 Composition of transparent soil
试验中所用的仪器与设备包括马氏瓶、流量计、渗透仪器、数码相机等(图2)。该装置可以实现如下功能:通过改变土样组分中硅粉各目数之间的比例关系,控制土体渗透系数;通过改变马氏瓶的位置,控制水力边界,研究不同性质土体、不同土壤压力条件下的修复药剂迁移规律。试验过程中通过流量计监测流速,均匀布置背景光源,降低外部光源对试验的影响,外置相机实时记录土样中药剂迁移的全过程。
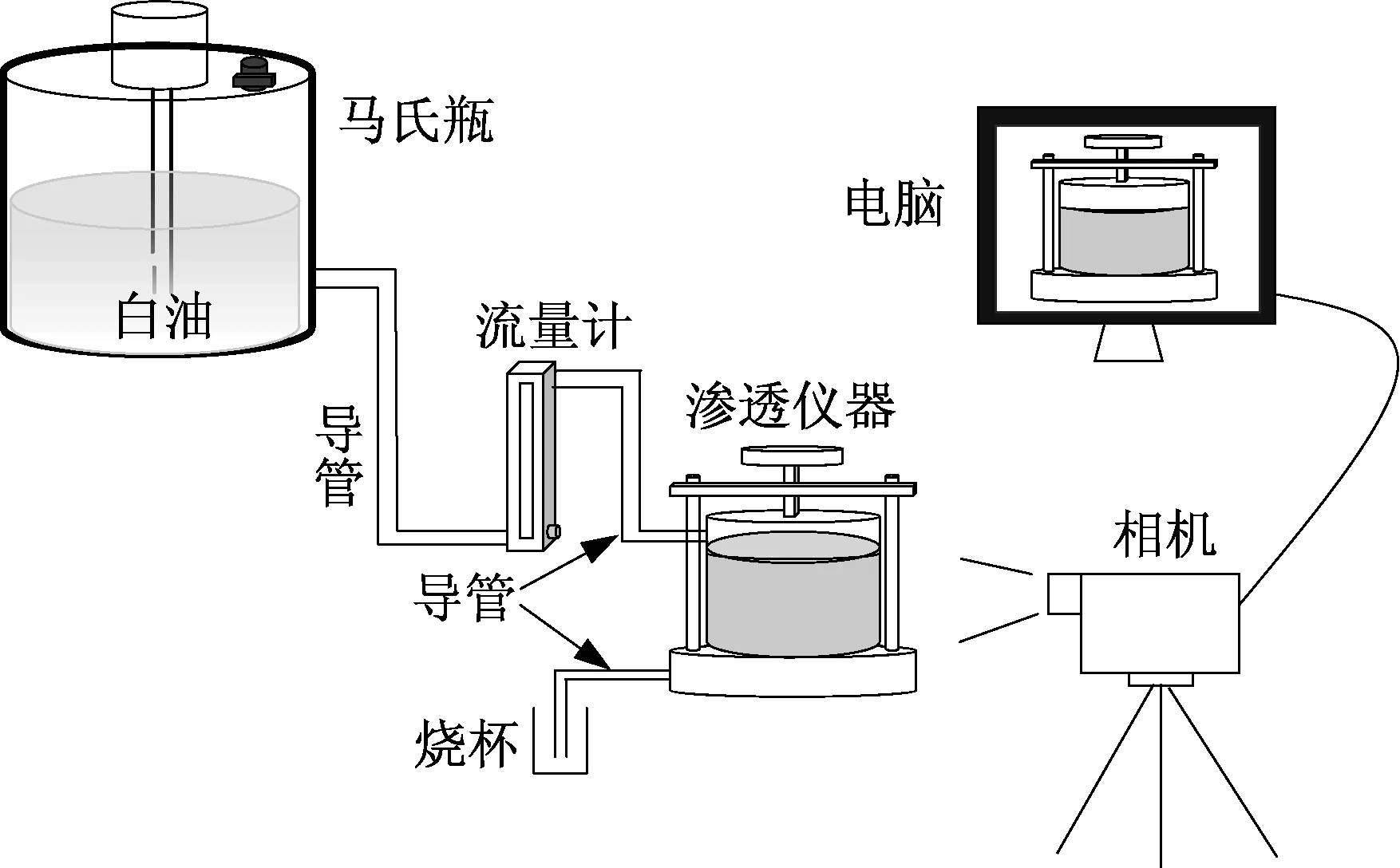
图2 试验装置简图Fig.2 Schematic diagram of test device
试验前先将所需各目数的硅粉充分混合,为使压样效果更好,边搅拌边滴入白油,搅拌均匀后放入制样器中,用千斤顶进行压样,压制完成后放入装满白油的容器中进行真空饱和,当试样完全饱和后,取出进行药剂迁移试验。因不同污染类型对应的药剂存在差异性,本文选取油溶性示踪剂代替修复药剂完成室内试验。
1.2 试验结果
试验选取的水头高度h 分别为1 m 和2 m,底部边界出流,相机采集到两种情况下不同时刻的示踪剂分布图像,如图3所示。由图中可以看出,水头越高,示踪剂迁移速度越快,当水头h=1 m 时,如图3a~3c,试验进行到第9 日,示踪剂迁移至试样盒底部;当水头h=2 m 时,如图3d~3e,试验进行到第6日,示踪剂已迁至盒底。另外,在示踪剂向下迁移过程中,两组试验中示踪剂迁移覆盖区域逐渐增大;水头越高,示踪剂分布区域越大,且较为分散。

图3 不同水头示踪剂迁移过程Fig.3 Migration process of tracer in different water heads
1.3 浓度的图像处理方法
配置1~1 000 g·m-3浓度区间内的示踪剂溶液,借助MATLAB 平台,标定浓度C 与灰度Q 的对应关系,曲线拟合得到式(1)。将迁移图像输入MATLAB平台,即可获得对应的等浓度线图。
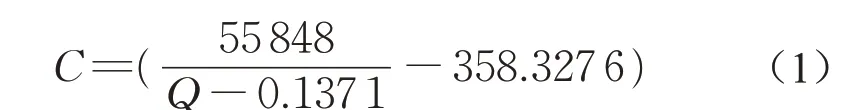
图3 中水头h=1 m 时的图像经过MATLAB 处理后得到的等浓度线图如图4所示,第3日时示踪剂迁移至泥饼高度三分之一处,浓度值范围为500~900 g·m-3,第6 日时示踪剂迁移至泥饼高度3/4 处,浓度值范围为400~600 g·m-3,第9 日时示踪剂迁移至泥饼底部,浓度值范围为300~500 g·m-3。当水头h=2 m 时,第3 日时浓度值范围为400~700 g·m-3,第6 日时浓度值范围为200~600 g·m-3。由于篇幅所限,这里没有给出h=2 m时的等浓度线图。

图4 示踪剂迁移等浓度线图Fig.4 Tracer migration equal concentration line diagram
2 数值模拟模型参数验证
溶质在土壤中的迁移基本通过两种形式:一是对流迁移,即溶质伴随土壤溶液的渗流而产生迁移;二是水动力弥散,即溶质在自身浓度梯度和土壤孔隙系统的作用下迁移。由此,溶质在土壤中迁移可建立对流-弥散模型。
应用Geostudio 软件中的SEEP/W、CTRAN/W 模块首先对第1 节的室内试验进行数值模拟,由于当采用透明土模拟天然粘性土时,土工试验测得透明土的渗透系数比实际值高1~2个数量级[19]。扩散系数为体积含水量的函数,体积含水量一定时,扩散系数为常数,在扩散试验过程中透明土试样的体积含水量是不变的,因此,认为扩散系数也是不变的。根据相同时间内药剂最大迁移距离相同的原则,由数值模拟与扩散试验结果一致来确定数值模拟参数,对数值模拟中的扩散系数和渗透系数进行了修正,计算结果表明采用修正参数获得的数值模拟结果与室内试验图像经MATLAB 处理后得到的结果基本一致。证明透明土材料可以应用于污染土修复药剂迁移特性的研究,之后采用修正后的模型参数对复杂工况下修复药剂的迁移规律进行了数值模拟。
在SEEP/W 模块中,分析类型为稳态分析。具体参数按照透明土样土工试验结果进行设置,泥饼高度为0.04 m,渗透系数为1.5×10-7cm·s-1,水头边界为1 m,并用四边形单元作为有限元分析的单元形式。渗流模型建立以后,应用CTRAN/W模块把渗流模型作为父项分析,即以渗流模型计算结果为基础,建立对流-弥散模型模拟示踪剂在透明土体中的迁移过程,扩散系数为关于体积含水量的常函数1×10-10m2·s-1,上边界初始浓度C(单位:g·m-3)设置为分段函数,见式(2),下部为出流边界。

经计算得到药剂迁移的浓度等势图(图5)。将其与迁移试验采集到的图像(图3)进行对比可以发现,示踪剂迁移到底部的时间为9日,随着时间的推移,示踪剂的浓度值变化与等浓度线图(图4)中基本一致。示踪剂不断向下迁移,最高浓度由3 d时的600 g·m-3逐渐减小至320 g·m-3,且示踪剂迁移覆盖的区域逐渐扩大。药剂的迁移规律、特定时间下的最大迁移距离以及迁移至泥饼底部所需的时间基本与试验结果相符。当水头为2 m 时,数值模拟的规律同样与迁移试验一致。因此,应用Geostudio数值模拟软件对土样中药剂迁移规律进行研究是可行的。
3 不同旋喷工况数值模拟
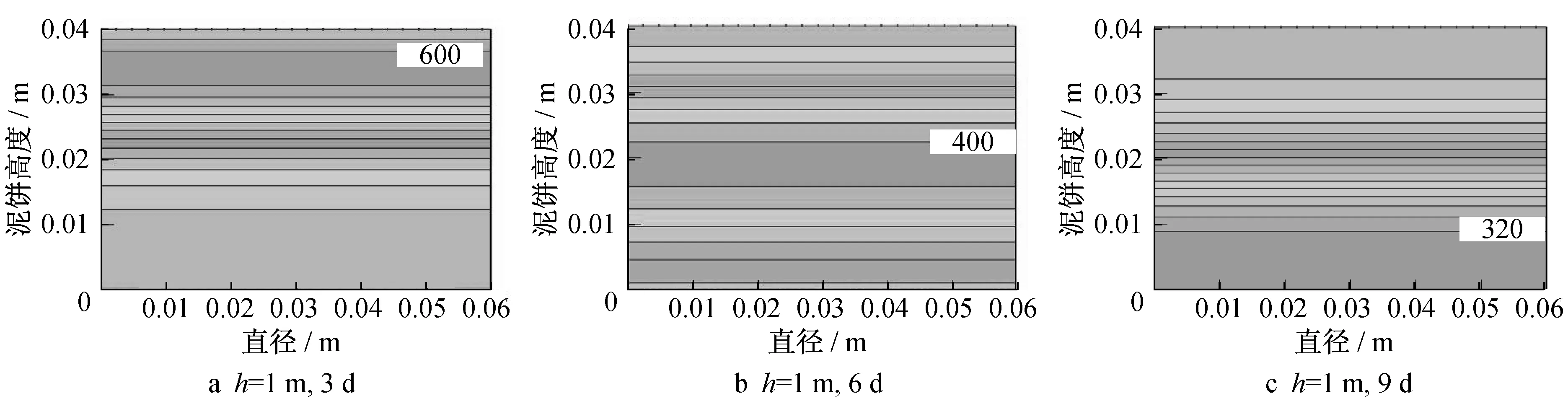
图5 药剂迁移浓度等势图Fig.5 Concentration equipotential diagram of medicament migration
高压旋喷污染土壤修复药剂迁移的实际工况往往更为复杂,同时很难进行大量的重复性现场试验,为此,这里在之前数值模型与参数已经确定的基础上,考虑泥饼高度、溶质扩散系数和初始浓度分布等因素进行了多种工况的数值模拟。
3.1 不同泥饼高度和压力边界
不同泥饼高度、不同压力边界条件工况如图6所示。取泥饼高度H 为0.04、0.06、0.1 m,渗透系数为2×10-7cm·s-1,单位体积含水量为0.688 m3·m-3,上边界压力P1分别为10、50、100 kPa,边界浓度C函数依据式(3);下边界压力P2和浓度均为0。
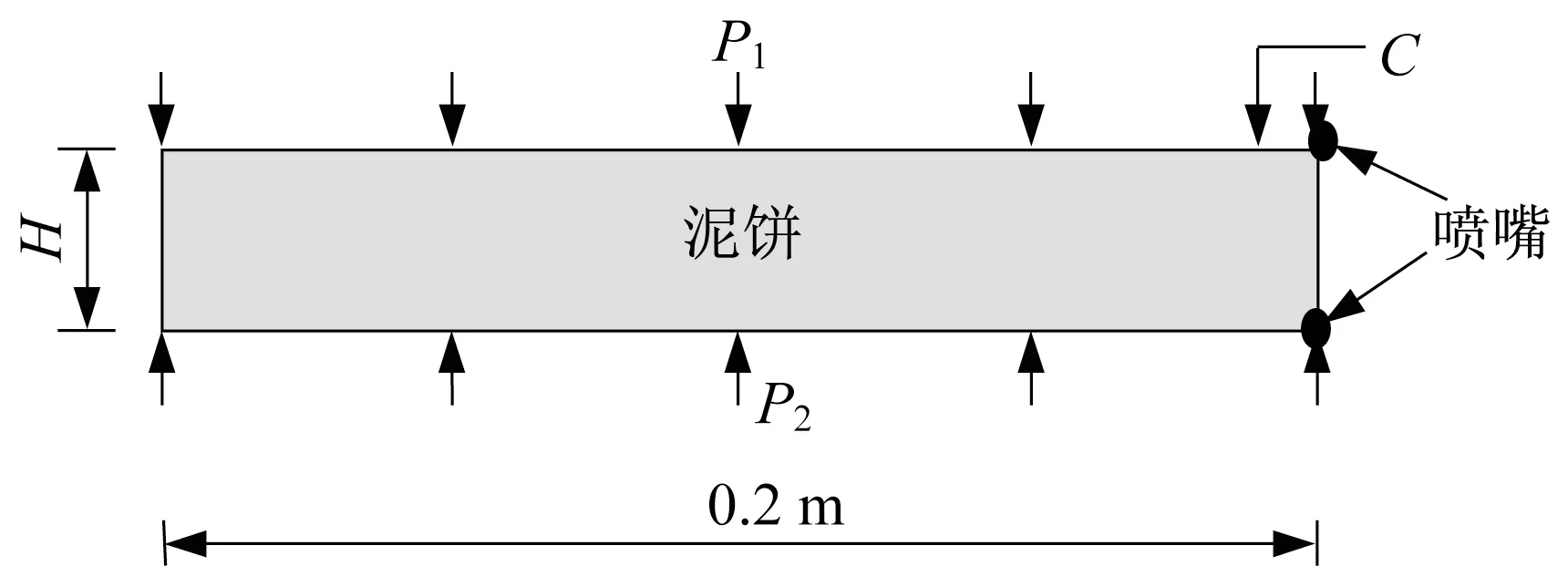
图6 不同泥饼高度、不同压力边界下的模拟工况Fig.6 Simulation conditions of different mud cake height and different pressure boundary

经计算,选取各边界条件下泥饼底部最早达到最大浓度的时间为结束时间,泥饼高度为0.04 m,上边界压力为10、50、100 kPa时,分别在第5日、第1.5日、第0.75 日时泥饼底部浓度达到最大值,其中压力条件为10 kPa下的浓度等势图如图7所示。再依次对泥饼高度为0.06、0.1 m的模型进行分析,控制除泥饼高度外其余参数与高度为0.04 m 的设置保持一致,泥饼高度为0.06 m 时,边界压力为10、50、100 kPa 时,分别在第10 日、第3.5 日、第1.5 日时完成;泥饼高度为0.1 m时,则分别在第23日、第6日、第3.5日时完成。可见,在同一泥饼高度下,土壤所处的压力越大,药剂到达泥饼底部的时间越短,且迁移速度表现出加快的趋势。
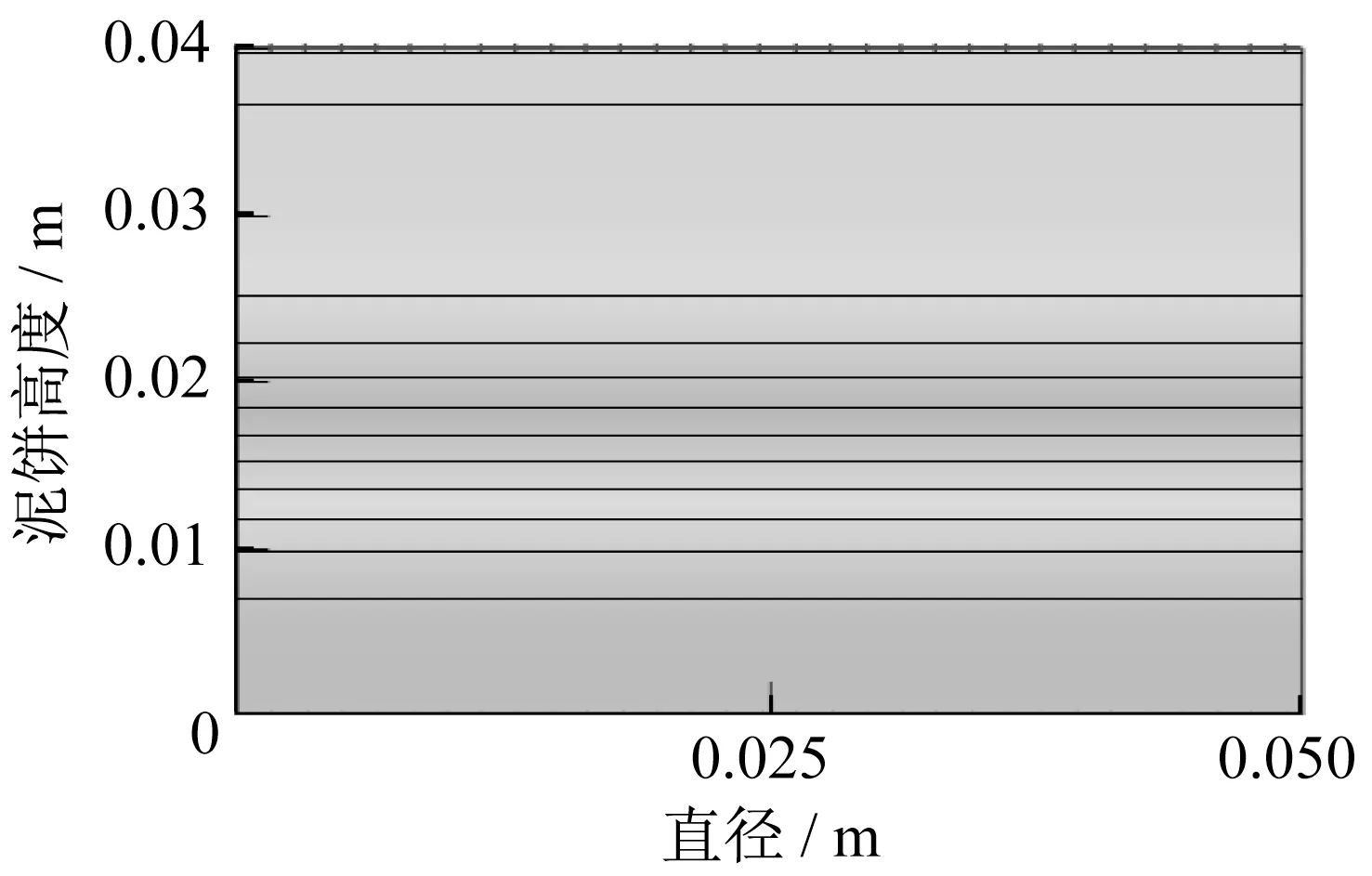
图7 浓度等势图(第5日)Fig.7 Concentration equipotential diagram (Day 5)
选取泥饼高度为0.04 m,土壤压力为100 kPa时,泥饼底部药剂浓度达到最大值时的时间步(即第0.75 日时),作土样中部竖向剖面节点的浓度-高度关系曲线,如图8所示。由图中可以看出,顶部压力为100 kPa时,泥饼底部已经达到药剂浓度的最大值,而10 kPa 和50 kPa 时的最大浓度仅分别迁移至泥饼顶部和1/4高度处。
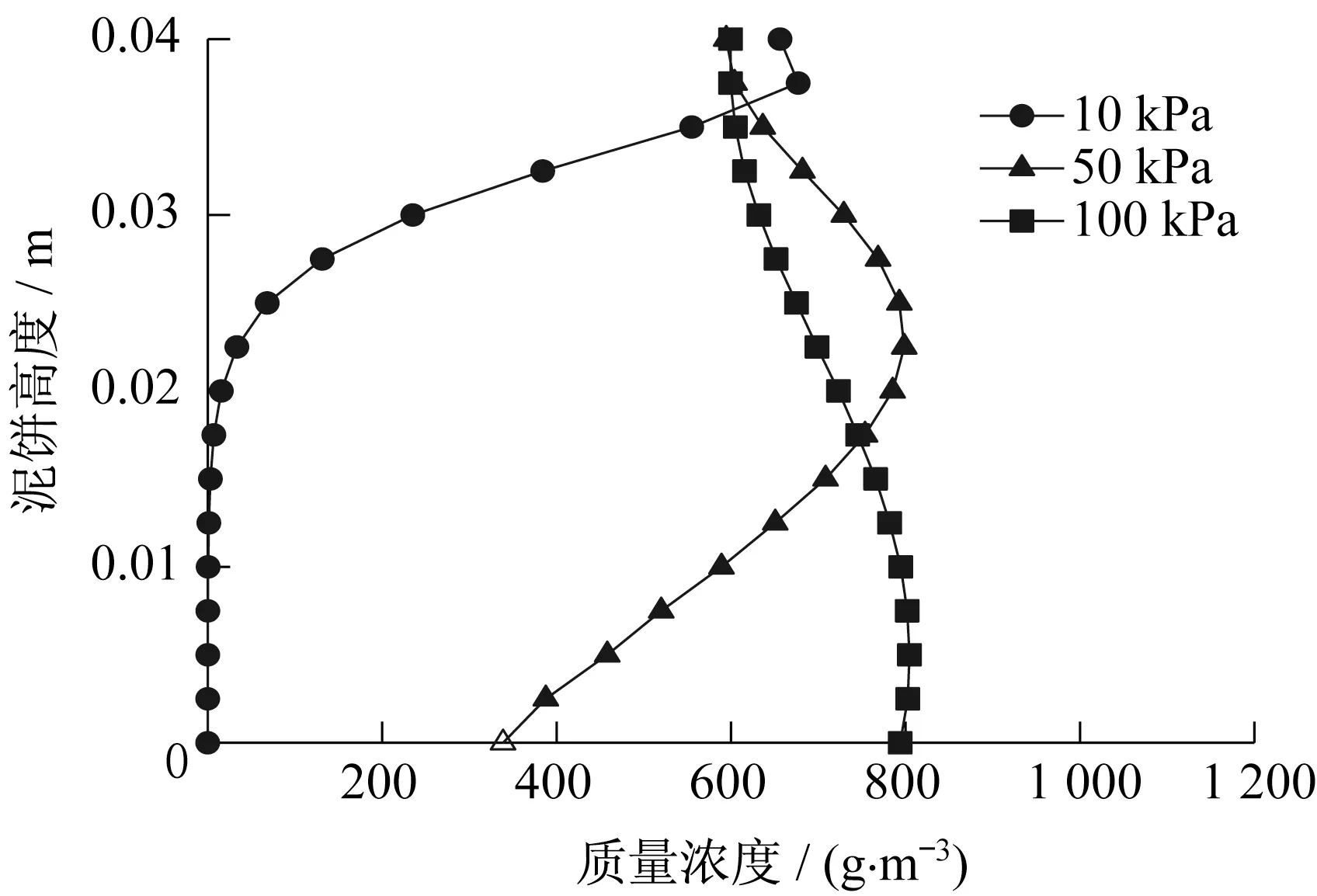
图8 中部竖向剖面节点浓度随泥饼高度的变化图Fig.8 Variation of node concentration in middle vertical section changing with mud cake height
选取泥饼高度为0.04 m,土壤压力为10 kPa时,泥饼底部达到最大浓度值时的时间步(即第5日),考察不同泥饼高度下泥饼中部竖向剖面节点的浓度变化,如图9 所示,此时,泥饼高度为0.06、0.1 m 的浓度最大值仅分别迁移至泥饼的中部、1/5 处,且泥饼高度越高,浓度最大值越小。因此实际修复工程中,泥饼高度的设定即高压旋喷参数的选取对修复效果及效率有重要影响。
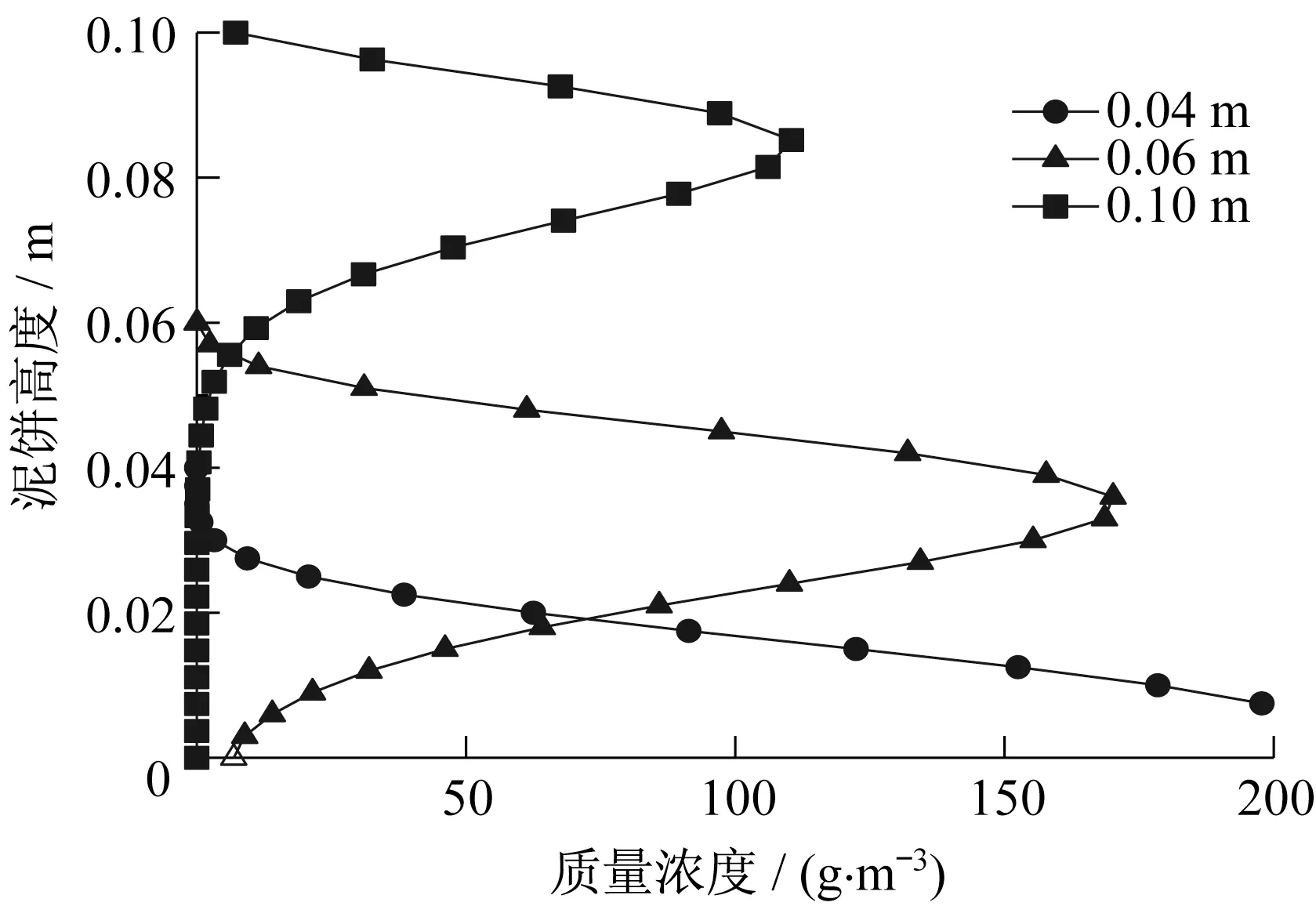
图9 不同泥饼高度下竖向剖面浓度对比(第0.75日)Fig.9 Comparison of vertical profile concentration at different mud cake heights (Day 0.75)
3.2 不同扩散系数
图10 所示为不同扩散系数下的模拟工况示意图,泥饼高度H=0.04 m,P1=20 kPa;P2=15 kPa;边界浓度函数见式(3)。
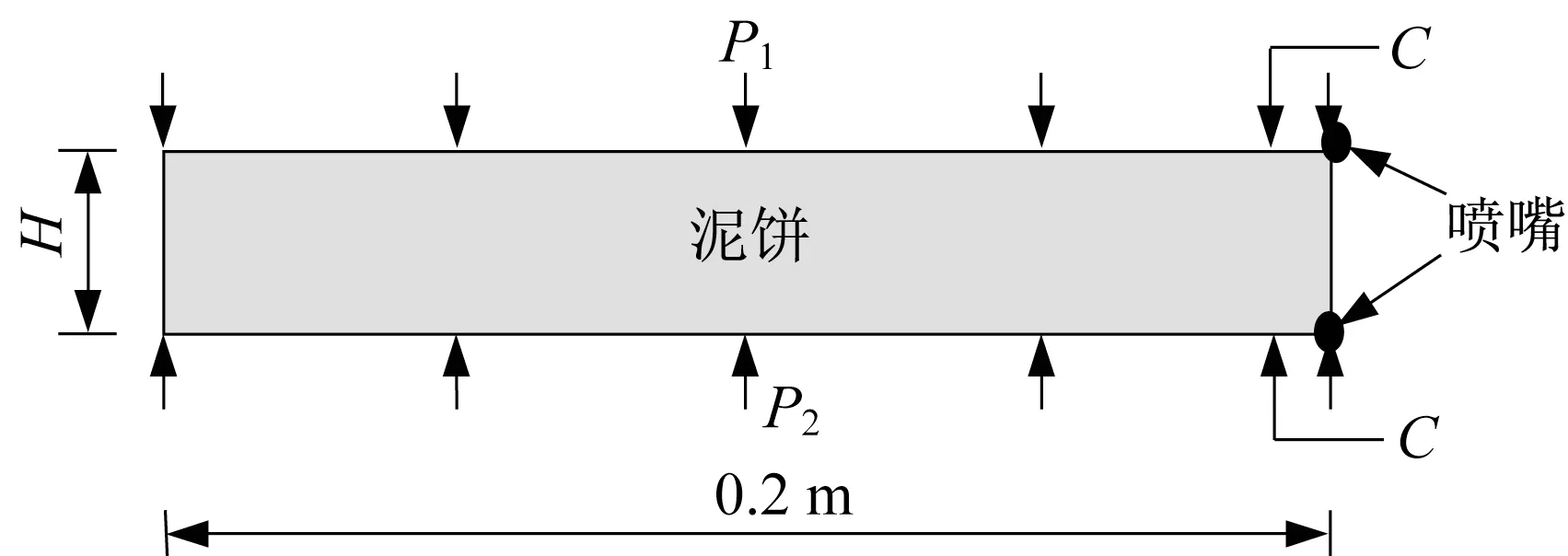
图10 不同扩散系数下的模拟工况Fig.10 Simulation conditions with different diffusion coefficients
在旋喷施工后,影响药剂迁移速度的最主要参数是土中扩散系数,取扩散系数D 为1.00×10-10、5.00×10-10和10.00×10-10m2·s-1分别计算,泥饼底部浓度分别在第8.5、6、4.5 日时达到最大,其中扩散系数为1.00×10-10m2·s-1的泥饼在第8.5日时浓度分布如图11 所示,随着时间推移,扩散系数较大的泥饼中,高浓度值覆盖区域更宽。
第4.5日时不同扩散系数下泥饼中心竖向剖面节点浓度随泥饼高度分布如图12 所示,此时,扩散系数为10.00×10-10m2·s-1的泥饼底部浓度已经达到最大值,而扩散系数为1.00×10-10、5.00×10-10m2·s-1泥饼中最大浓度值仅迁移至泥饼高度的1/2 位置处,可见扩散系数越大,迁移速率越快;扩散系数为1.00×10-10m2·s-1的泥饼中心与顶部、底部的药剂浓度相差较大,而扩散系数为5.00×10-10、10.00×10-10m2·s-1的泥饼浓度随高度的变化较小,且前者泥饼中心的浓度接近后两者的两倍。
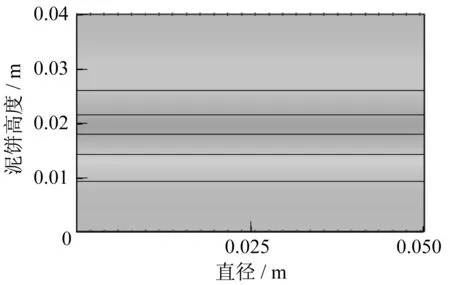
图11 浓度等势图(第8.5日)Fig.11 Concentration equipotential diagram (Day 8.5)
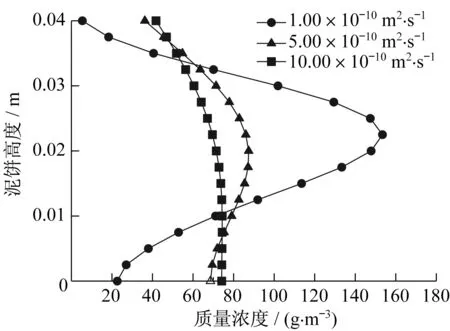
图12 泥饼竖向剖面浓度随泥饼高度分布(第4.5日)Fig.12 Distribution of vertical profile concentration of mud cake changing with mud cake height(Day 4.5)
3.3 边界浓度沿水平方向递减
图13 所示为边界浓度沿水平方向递减时的模拟工况示意图,泥饼高度H=0.04 m,土的扩散系数为5.00×10-10m2·s-1,P1=20 kPa,P2=15 kPa,假定旋喷直径为0.2 m,边界浓度函数如图14所示。
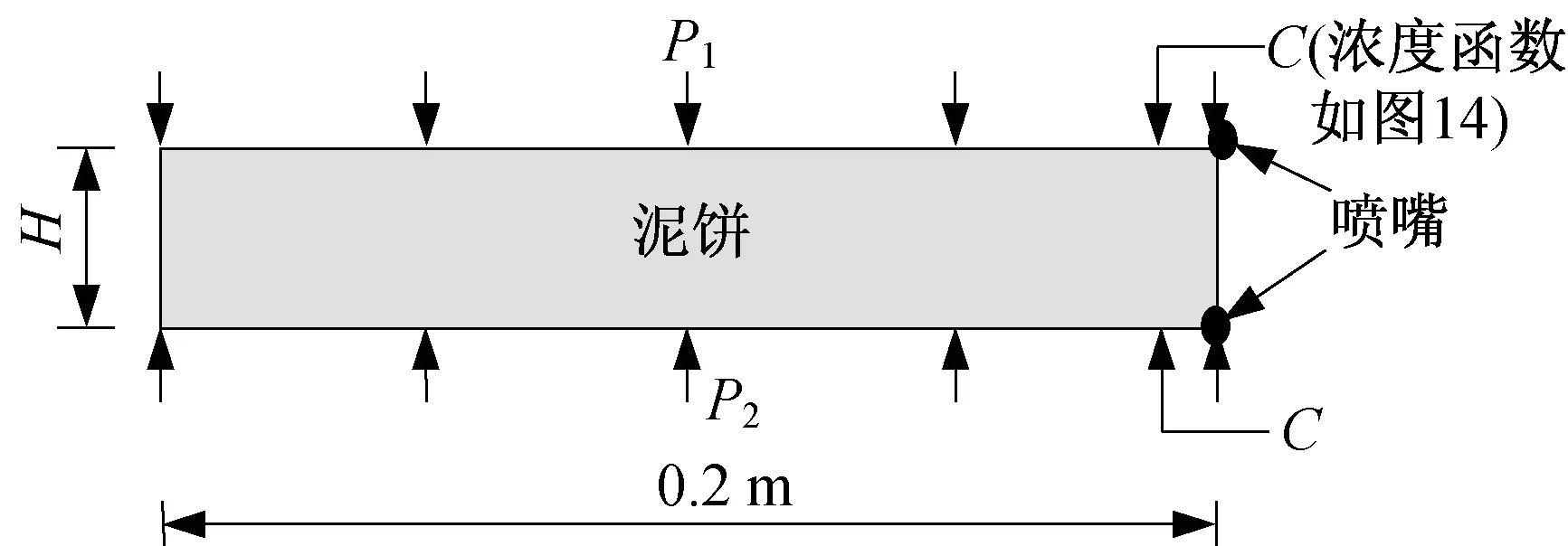
图13 边界浓度沿水平方向递减时的模拟工况Fig.13 Simulation of boundary concentration decreasing along horizontal direction
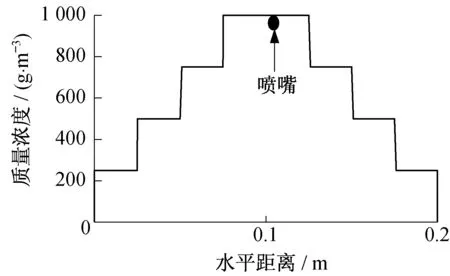
图14 边界浓度示意图Fig.14 Boundary concentration diagram
对图14中对称浓度边界的左半部(0~0.1 m)进行分析,经计算,当边界浓度从喷嘴处沿径向向外阶梯形递减时(由1 000 g·m-3降低至250 g·m-3),第1、5 日后泥饼中离喷嘴不同距离处药剂浓度分布示意图,如图15 所示。从图中可以看出,旋喷中心浓度高,边缘浓度低,由第1日至第5日,药剂浓度在水力梯度作用下以竖向迁移为主,水平方向的迁移不明显,随着边界浓度沿水平方向的递减,泥饼中心也呈向边缘递减的趋势。
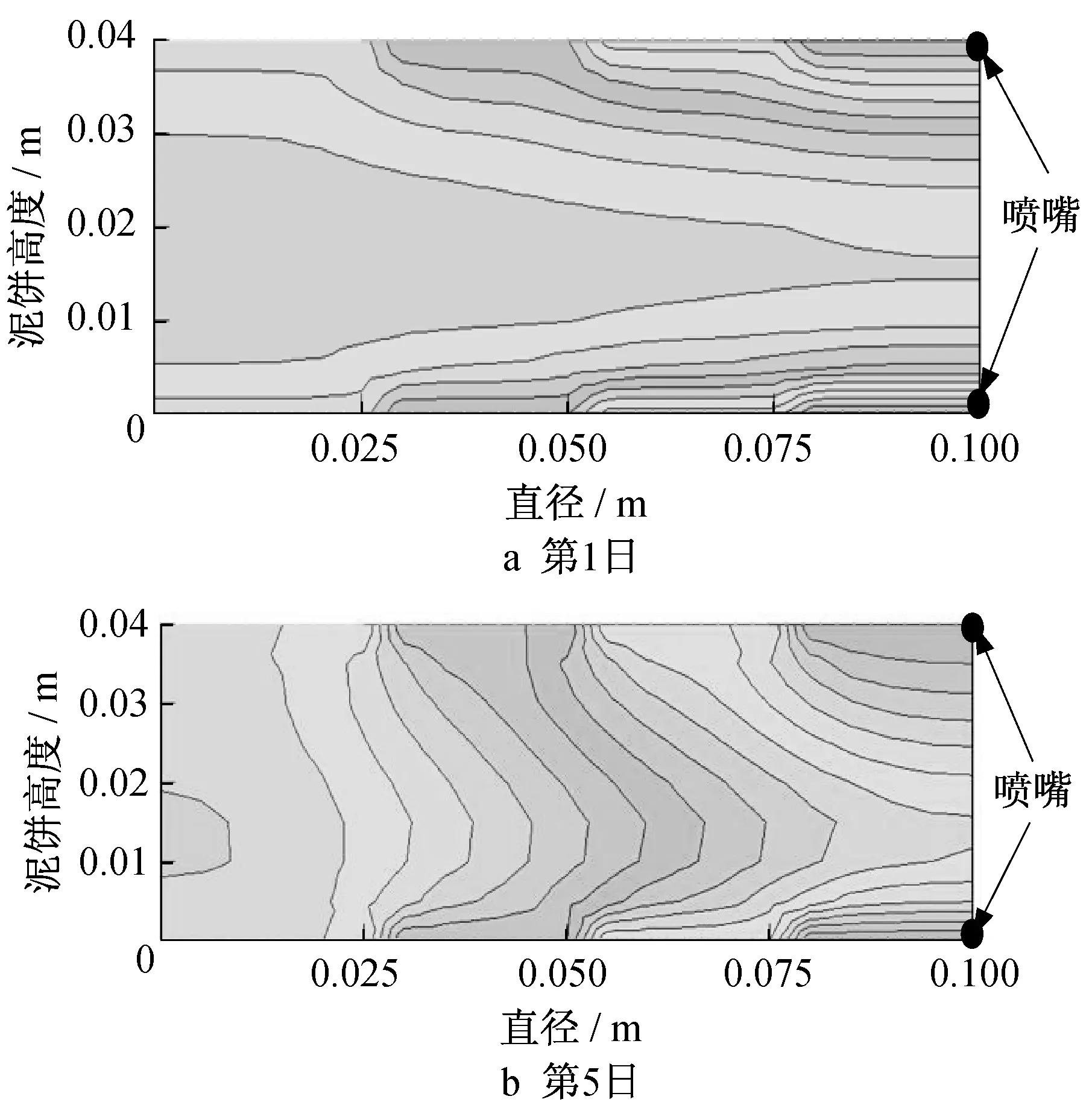
图15 浓度随时间变化的等势图Fig.15 Isopotential diagram of concentration changing with time
图16 为第5日时离旋喷桩喷嘴不同水平距离处的泥饼中药剂浓度沿高度分布示意图,中心浓度分布情况基本与边界药剂浓度分布情况一致。喷嘴位置处浓度较高,沿泥饼高度的变化更为明显,泥饼中心处浓度为边界处的65%;距离喷嘴位置越远,泥饼中浓度沿高度的变化越小,距喷嘴为0.025 m 处泥饼中心浓度约为边界处的80%,距喷嘴为0.05 m处泥饼中心浓度约为边界处的84%;距喷嘴为0.075 m 处浓度沿高度的分布更为稳定,泥饼中心浓度与边界初始值十分接近。由图中可以发现,在一定时间范围内,泥饼中药剂迁移以竖向迁移为主,所以为使实际工程中药剂以高浓度均匀分布至泥饼边缘,需保证药剂在泥饼间隙水平方向以较高的浓度均匀分布。
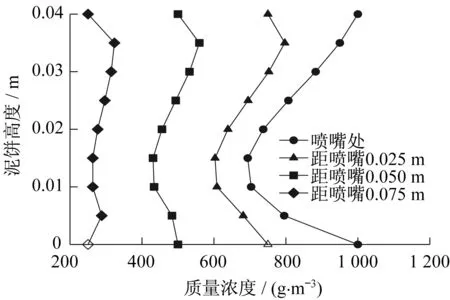
图16 药剂浓度沿高度分布(第5日)Fig.16 Distribution of medicament concentration along height(Day 5)
4 结论
本文基于透明土可视化试验技术,对应用高压旋喷注药技术后形成的泥饼进行了修复药剂迁移的室内试验和数值模拟,得出如下结论:
(1)同一泥饼高度下,土样所处的压力越大,迁移速度越快;同一土壤条件下,泥饼高度越高,其底部达到浓度最大值所需的时间越长,且浓度最大值越小。因此实际修复工程中应确定最佳泥饼高度。
(2)扩散系数较大的泥饼中迁移速率较快,且高浓度值覆盖区域更宽;在一定范围内,扩散系数倍数增大时,浓度最大值也呈倍数增大。
(3)药剂浓度在水力梯度作用下以竖向迁移为主,水平方向的迁移不明显,随着边界浓度沿水平方向的递减,泥饼中心也呈向边缘递减的趋势,且中心浓度分布情况基本与边界药剂浓度分布情况一致。实际工程中需保证药剂在泥饼间隙水平方向以较高的浓度均匀分布,才能使药剂以高浓度迁移至泥饼边缘。
