盾构隧道同步注浆纵环向整体扩散理论模型

李培楠，石 来，李晓军，刘 俊

（1. 同济大学土木工程学院，上海200092；2. 东华大学环境科学与工程学院，上海201620；3. 上海工程技术大学城市轨道交通学院，上海201620）

盾构工法是城市地下空间开发的主要施工方法之一，刀盘掘进、管片拼装和同步注浆构成了盾构工法的三大要素。同步注浆在控制环境扰动、隧道抗浮防渗等方面起到关键作用，然而由于不可见性，具有较大的不确定性和风险性。注浆参数的设定直接影响注浆效果，而针对浆液材料特性及地层环境特点如何正确取值则依赖于注浆机理分析及其扩散模型的指导。

长期以来，不少学者对浆液扩散机理和理论模型开展了相关研究。张庆松等［1］研究速凝类浆液在水平裂隙中的扩散流动过程，并考虑了浆液黏度的时变性，建立了水平裂隙注浆扩散理论模型。张连震等［2］在此基础上，考虑了浆液和岩体之间的相互作用，并建立了可完整描述考虑耦合作用的注浆扩散过程的数值算法。裴启涛等［3］则进一步将该注浆扩散理论推广到倾斜裂隙注浆。

盾尾注浆是盾构同步注浆的主要形式。针对盾尾同步注浆扩散模型，许多学者也进行了研究。Bezuijen 等［4-5］分析了浆液从填充、渗透到压密的整个扩散和固结过程，并结合现场注浆测试研究，探究不同阶段浆液压力的变化。叶飞等［6-8］将浆液在盾尾间隙内的扩散过程理想化地归纳为充填、渗透、压密及劈裂等4个阶段，并分别展开了理论分析研究。李志明等［9］分别采用牛顿流体及Bingham 流体推导出了在黏土地层中同步注浆填充扩散的力学模型。袁小会等［10］基于Bingham 流体本构，推导出了注浆压力时空衰减规律以及扩散距离与注浆时间的关系。梁禹等［11］在已有的研究基础上，综合考虑了同步注浆过程中的浆液填充、扩散与后续因渗流引起的压力消散过程，并得到了浆液压力沿管片环纵向分布的理论计算公式。

分析上述学者的研究内容，可以发现浆液在盾尾间隙内的环向填充和纵向扩散往往被看作两个相互独立的运动模式，关于浆液纵环向整体扩散理论模型的研究较少。本文在现有的浆液扩散理论研究基础上，分析盾尾同步注浆纵环向整体扩散机理，建立盾尾同步注浆空间扩散理论模型，并提出求解该模型的数值算法。此外，依托大直径圆形盾构隧道工程实例，对模型进行验证和分析。

1 盾尾同步注浆扩散机理

1.1 机理分析

文献［8-9］和文献［11］中的理论推导主要研究浆液环向独立扩散时的压力分布情况，其假设在盾尾同步注浆过程中，浆液环向填充可忽略其沿隧道轴向的流动，填充空间被假定成一个均匀的三维环状薄饼，而浆液纵向扩散也视为环向填充完成后，横截面内浆液的一致纵向扩散。然而，实际上由于注浆口的出浆速度远大于盾构推进速度，因此浆液环向填充过程不可忽略浆液的纵向扩散运动，即浆液的扩散模式应是具有纵环向相互关联的（图1），上述假设在一定程度上与实际情况有着较大的偏差。

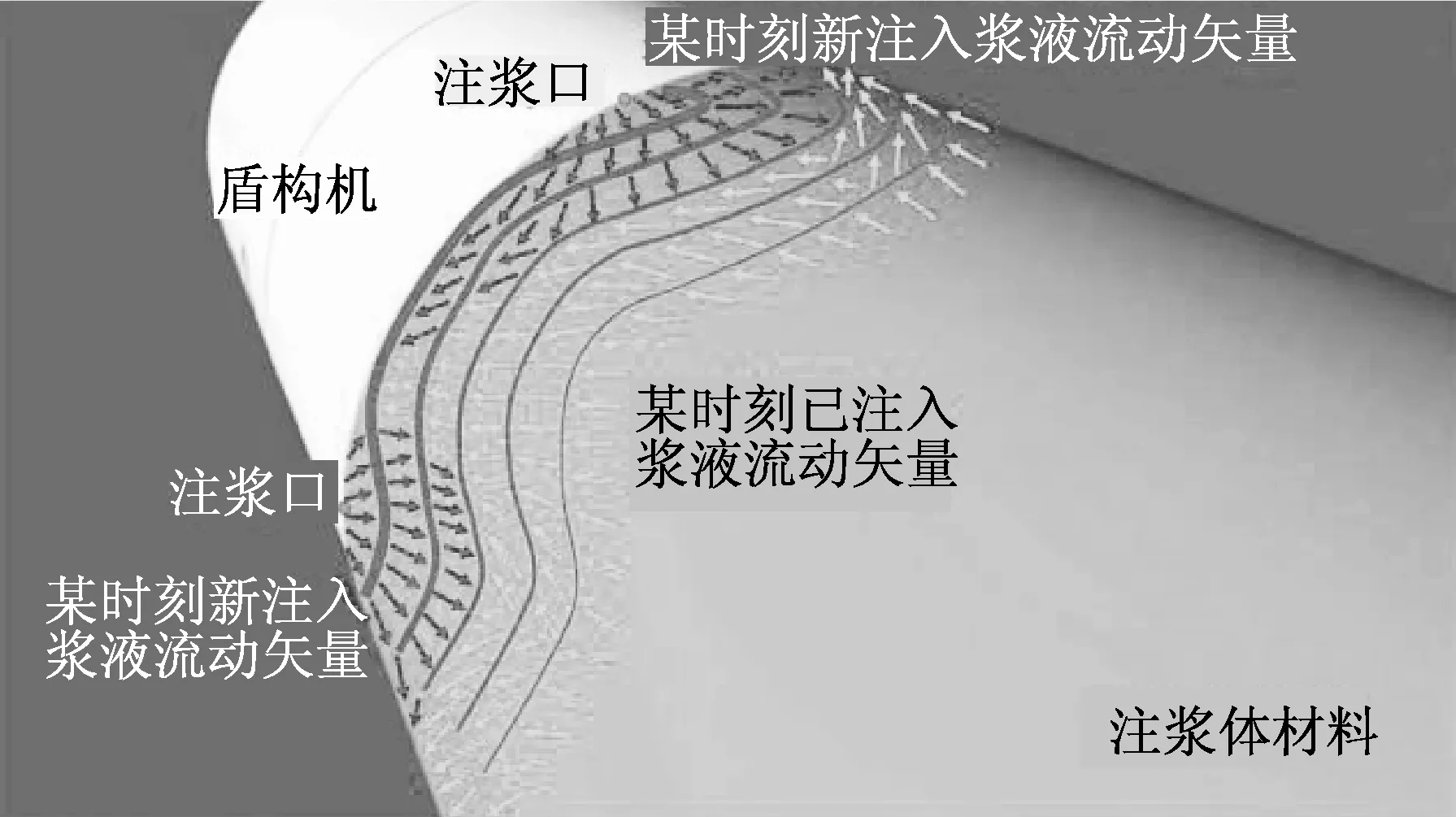
图1 同步注浆纵环向三维扩散机理示意图［12］Fig.1 Schematic of synchronous grouting longitudinal-circumferential 3D diffusion mechanism[12]

参考文献［12］，盾尾同步注浆光滑粒子流体动力学（smoothed particle hydrodynamics，SPH）数值模拟结果显示浆液注入盾尾间隙是一个空间动态的填充过程，浆液由注浆孔喷出后呈现扇形扩散的模式（图2），浆液的扩散形态由注浆参数和周围环境压力决定。因此，盾构隧道盾尾同步注浆的填充扩散过程整体上应当被看作是具有纵环向相互关联的挤压填充性流体运动。

图2 浆液扩散形态的数值模拟结果［12］Fig.2 Numerical simulation results of grout diffusion form[12]

1.2 基本假设

基于盾尾同步注浆扩散机理分析，为后续理论公式推导提出以下基本假设：

（1）浆液为各向同性不可压缩的Bingham流体，不考虑浆液损失及黏度等性质变化；

（2）浆液与地层、管片外壁接触面不发生相对滑移，浆液为层流状态；

（3）浆液扩散锋面处压力等于周围环境压力，任意浆液单一质点的流动方向与管片轴线的夹角保持不变；

（4）浆液出注浆孔时的初始扩散锋面为半圆形，扩散运动平衡方程不考虑加速度影响。

1.3 浆液扩散运动方程

图3 为盾尾同步注浆浆液扩散示意图，直线填充部分代表新注入浆液，网格填充部分代表已注入浆液。M 位于浆液扩散锋面上，N 为M 与注浆孔1连线H1M上的任意一点，Nt为N在隧道横截面上的投影。图3中，α1为注浆孔1与所在截面管片中心连线的竖向夹角，αN为N 与所在截面管片中心连线的竖向夹角。假定浆液扩散方向与管片轴线的夹角保持不变，则在管片外表面展开图中，浆液扩散方向始终与注浆孔与扩散锋面的连线同向。即如图4 所示，H1M 连线上任一点N 的速度vN存在vN//H1M，与管片轴线的夹角为θM（逆时针为正）。

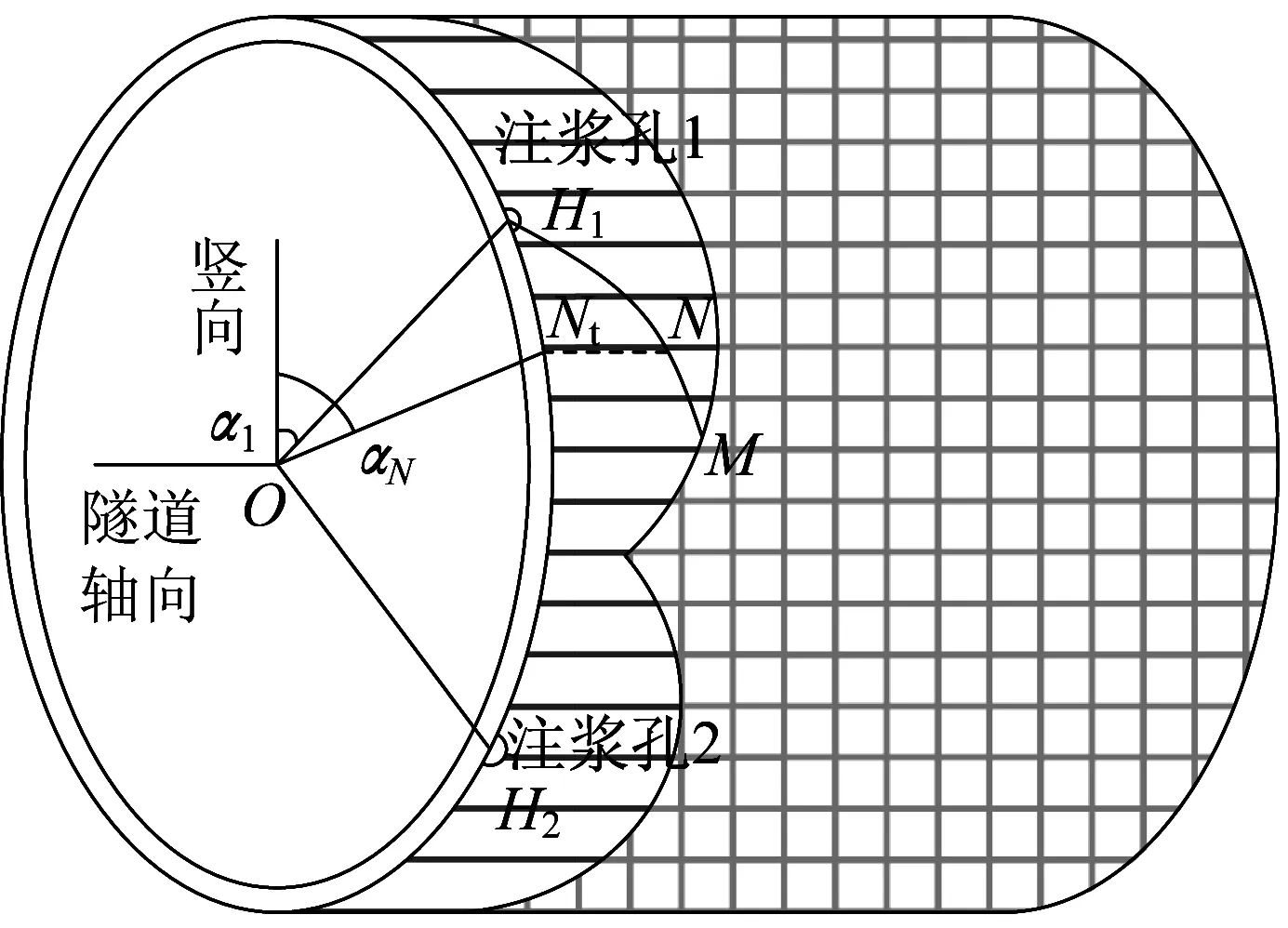
图3 浆液扩散立体示意图Fig.3 Stereoscopic diagram of grout diffusion

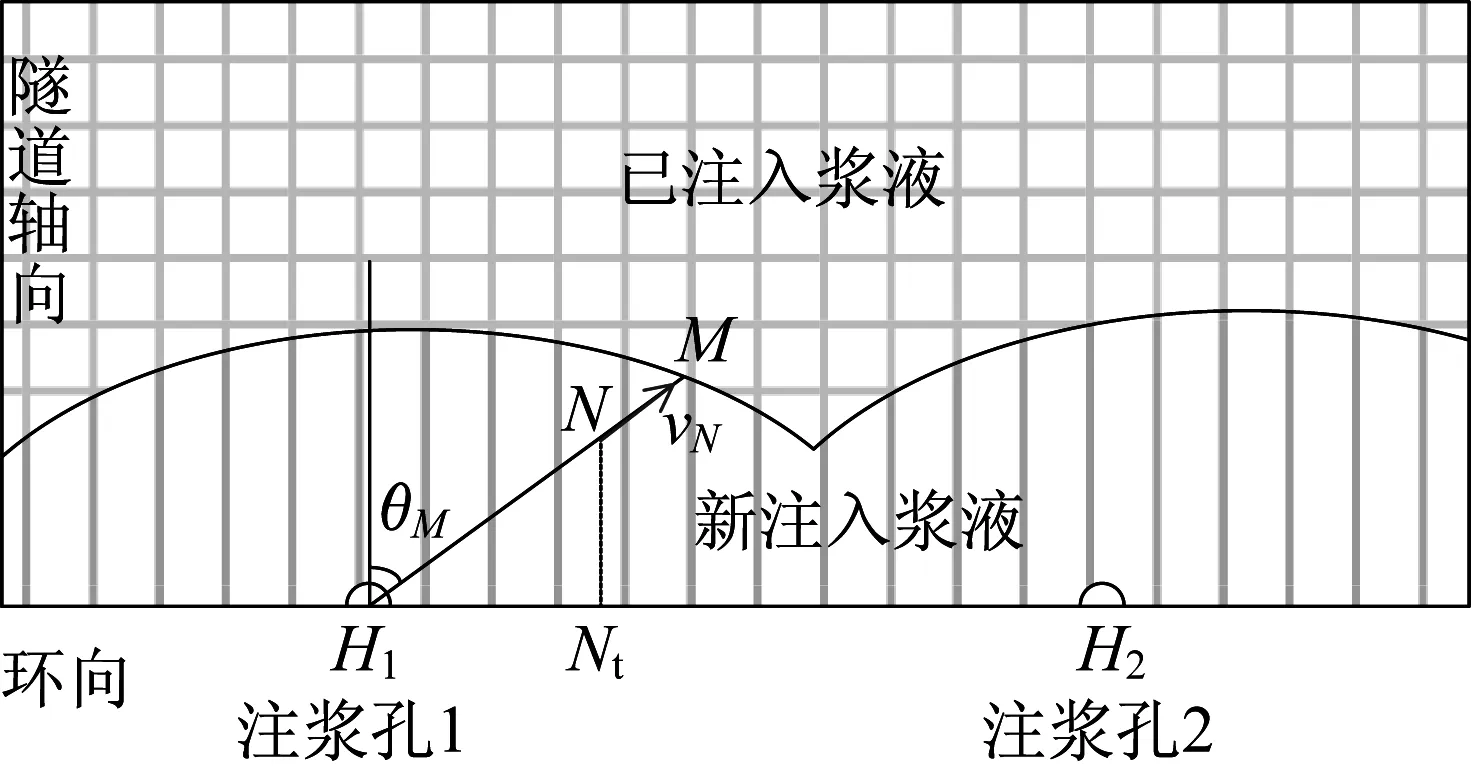
图4 浆液扩散平面展开图Fig.4 Plane stretched diagram of grout diffusion

如图5所示，取N处浆液微元进行分析。图中，Z，R，S 分别表示盾尾间隙厚度方向，浆液流动方向和该平面外法向；w 为盾尾间隙厚度；zp为Bingham流体流核半径；P 为浆液压力；τ 为浆液运动的剪应力。沿着浆液流动方向对浆液微元进行受力分析，可得：

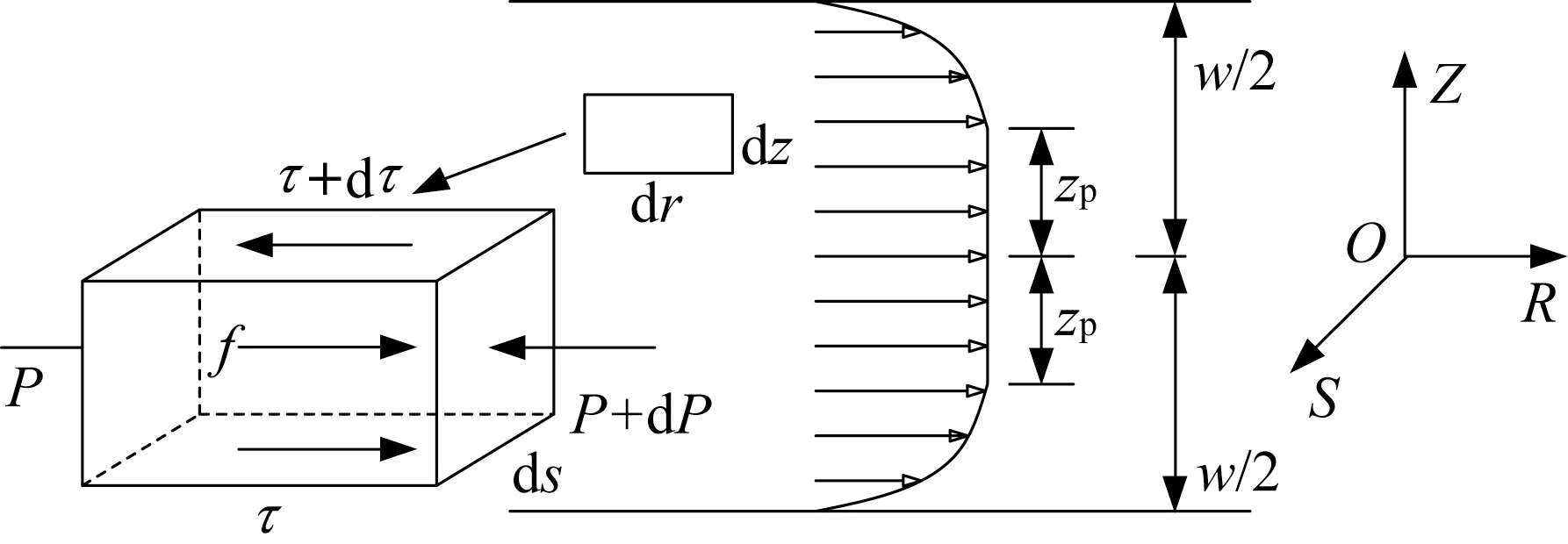
图5 浆液微元受力分析图Fig.5 Mechanical analysis of grout element

式中：f为重力在R方向上分量，f =ρg sin αNsin θM；ρ为浆液密度；g为重力加速度。

假定浆液为Bingham流体，其本构方程为

式中：τ0为静切力；μ为塑性黏度系数；γ为剪切速率；v为浆液流动速度。

将式（4）代入式（3）得到：

令τ0=Az/R，可得Bingham流体的流核半径：

在|z|≤zp范围内，流体切应力较小，流层之间不发生相对流动；在zp≤|z|≤w/2 范围内，流体切应力逐渐增大，相邻层流体处于运动状态，如图5所示。

对式（5）进行积分，联合边界条件：z=w/2 时，v=0，得浆液在zp≤|z|≤w/2范围内速度分布：

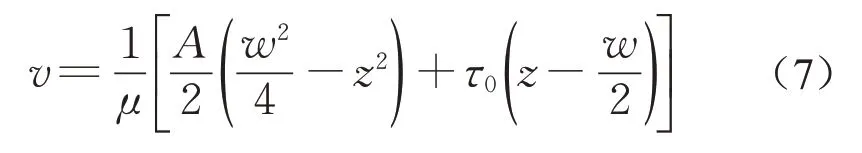
流核半径内浆液流速一致，则浆液流速沿z方向的分布为

建立微元截面流量与浆液流速的关系式：

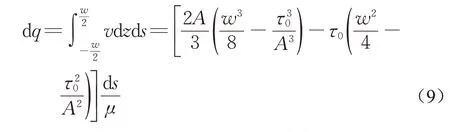
因此，可以得到A的一元三次方程：

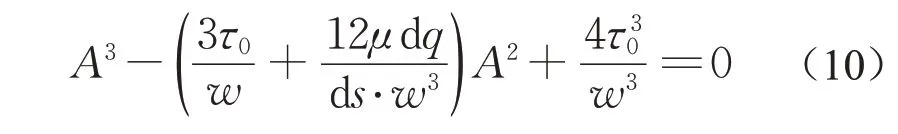
利用式（10），并联立式（6）的约束条件：zp＜w/2，可解出A的值。

由式（2）可得：

基于浆液质点扩散速度方向始终与管片轴线夹角不变假设，注浆孔与扩散锋面一点的连线上的各个点的浆液扩散速率的关系式如下：

基于浆液扩散锋面处压力等于周围环境压力的假设，可得浆液扩散运动的控制方程为

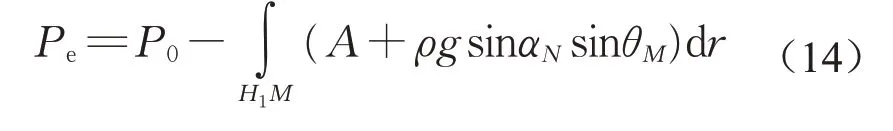
式中：P0为注浆孔压力；Pe为环境压力。

2 盾尾同步注浆步进式算法

理论推导得到的计算公式中涉及多个多元非线性方程，且浆液扩散轨迹不规则进而无法直接积分，因此需借助数值方法进行求解注浆压力。

2.1 求解区域离散化

图6为注浆孔1浆液扩散范围的展开图，将扩散区域离散成n-1 个扇形单元，各扇形单元的圆心角Δθ 相等。此外将每个扇形单元沿着径向离散成m个等间距的环形单元，环形单元按照等数等分，相应边长Ri上的离散长度Δri具有自适应性。图6 中r0为注浆孔等效半径，rij代表Ri上第j个离散点距离注浆孔圆心的长度。

基于连续性假设，同一扇形单元内的不同环形单元流量相等，则各环形单元浆液扩散速度可由式（13）得到。

基于式（11），可得浆液经过环形单元ri，jri，j+1时产生的压力损失：

其中，Ai，j=f(ri，j，θi，Δq)，由式（10）计算可得。

式（15）中，环形单元的竖向夹角计算公式如下：

图6 浆液扩散区域内的离散单元划分Fig. 6 Division of discrete elements in the slurry diffusion region

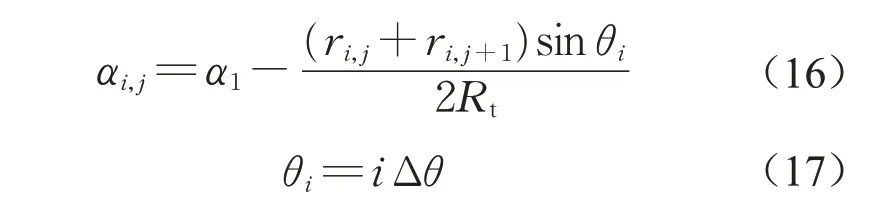
式中：Rt为盾构隧道外径。

2.2 基于弦截法的注浆流量求解

浆液扩散锋面的速度由注浆压力和周围环境压力的压力差决定，计算各个扇形单元的注浆流量Δqi需要求解以下的非线性方程组：

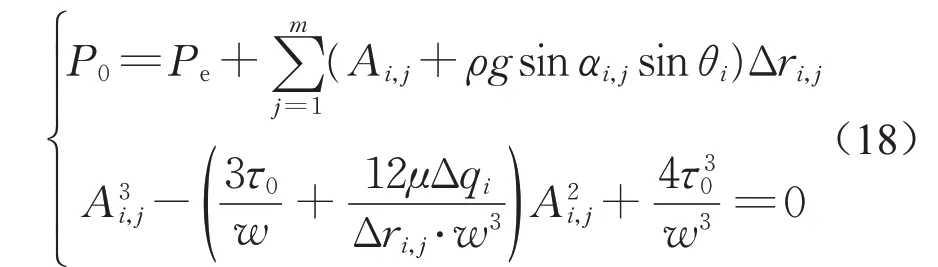
对于该类问题，弦截法是一种有效的数值计算方法。如图7所示（xs代表方程f(x)=0的精确解），弦截法是一种通过不断的线性迭代求解非线性方程的数值方法，相较于二分法，能够快速收敛至零点。弦截法的基本迭代公式如下：

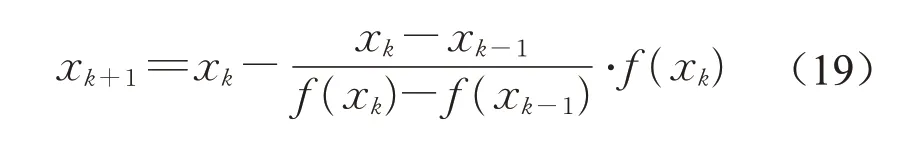
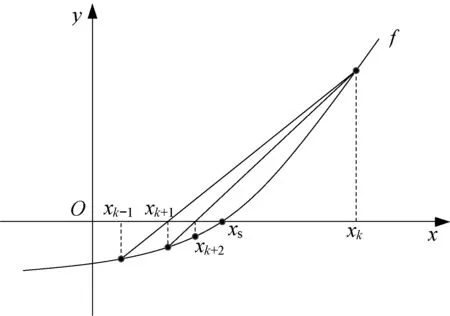
图7 弦截法迭代计算示意图Fig. 7 Schematic diagram of secant method iterative calculation

基于式（18），通过编写相应的算法程序，可获取满足误差要求的各个扇形单元的注浆流量的Δqi数值解。

2.3 浆液扩散锋面追踪

注浆扩散压力的计算前提之一在于明确浆液的扩散锋面，而扩散锋面是由不同点处浆液扩散速度决定的。因此，浆液扩散锋面与浆液扩散速度的求解是一个关于时间离散的交替迭代问题。

如图8 所示，迭代的初始状态T0为距离注浆孔一定范围内（半径R0），浆液扩散锋面为半圆形。通过初始扩散锋面，可求解该时刻的各个扇形离散单元的锋面扩散速度，进而求解浆液扩散半径增量。

图8 浆液扩散锋面步进式求解示意图Fig.8 Step-wise solution of grout diffusion edge

第Tk+1的扩散锋面计算公式如下：

式中：vˉi，k为第k时刻第i个扇形单元锋面处的平均流动速度；ΔRi为第i个扇形单元的流动路径增量。为保证计算精度，限制max(ΔRi)＜0.1m，因此时间增量ΔTk是可变的。

扩散锋面叠加扩散半径增量可得新的扩散锋面，继续下一轮计算。循环交替，可以获得浆液最终收敛状态下的扩散形态和压力分布情况。

2.4 数值算法计算流程

盾尾同步注浆算法流程如图9 所示，计算程序采用MATLAB编写，具体计算步骤如下：

（1）输入计算参数，其中几何参数包括隧道外径Rt、盾构间隙厚度w，施工参数包括注浆孔的竖向夹角α1、注浆压力P1以及注浆孔对应埋深处的环境压力Pd，计算参数包括扩散区域离散参数n 和m（图6），注浆孔等效半径r0，初始扩散半圆半径R0以及计算时步大小Δt；

（2）根据初始半圆扩散锋面，对浆液扩散区域进行离散；

（3）基于弦截法，给定第i 个扇形单元的注浆流量两个初始迭代解，计算该扇形单元每个离散环形单元前后的压力差；

（4）比较前后两个解的差异性，判断是否达到误差要求，进行下一次弦截法迭代；

（5）对所有扇形单元进行注浆流量迭代计算后，得到新的扩散锋面位置；

（6）基于新的扩散锋面进行新一轮循环计算；

（7）设定一个计算时间最大值tmax，该最大值通过预先试算确定，保证所有注浆孔的浆液扩散区域足够覆盖管片环向范围；

（8）记录Ri和Δqi，并基于此得到扩散区域内每一个离散点处的浆液压力。

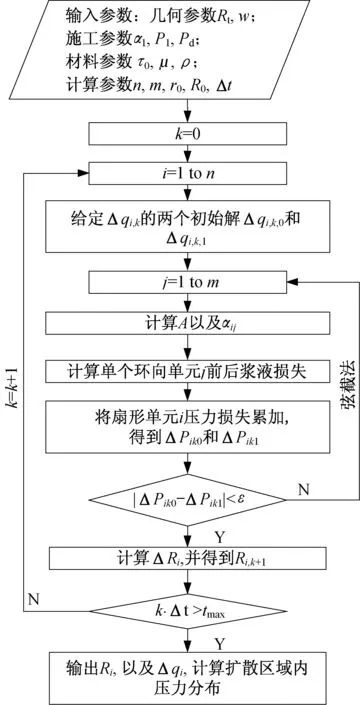
图9 算法流程图Fig.9 Flow chart of algorithm

3 工程实例分析

参考文献［4］中关于荷兰Sophia 铁路隧道的注浆压力监测数据，对1.3节中的理论公式和2.4节中数值算法进行验证。

3.1 工程概况

Sophia 铁路隧道位于荷兰Rotterdam 东南约20 km处，包含两条外径9.5 m，衬砌厚度0.4 m的圆形盾构隧道。试验点处，两条隧道间距10 m，隧道顶部埋深14 m。地层情况如下：地表以下首先为12 m厚全新世土层，包含泥炭土（2/3）和黏土（1/3）；其次为10.7 m厚的中密砂土，隧道位于该土层；砂土层下方为泥炭土和粉质黏土层。在隧道试验截面处，地下水距地表深度约为1 m，隧道顶部的覆土压力大致为200 kPa。

Sophia铁路隧道盾构施工采用典型的六孔注浆方案，注浆孔布设以及注浆压力见表1，其中环境压力是指上一环管片推进时注入的浆液在稳定之后的压力值。参考文献［4］和文献［13］，环境压力竖向变化梯度取为15 kPa·m-1，拱顶环境压力取值为上覆土压力200 kPa。盾尾间隙厚度为0.16 m，浆液物理力学参数见表2。其中，注浆压力一般情况下应略大于环境压力，实际施工中注浆压力常出现波动，计算中通常取对应工况下的单环推进稳定时的平均值。本文基于文献［4］中的现场实测数据，选择测试截面刚脱出盾尾后（此时的实测压力值最接近真实的注浆压力值），邻近注浆孔位置的测试点的浆液压力局部平稳值作为注浆压力值。

表1 Sophia隧道注浆孔布置Tab.1 Layout of grouting holes for Sophia tunnel

表2 同步注浆浆液物理力学参数Tab.2 Physical and mechanical parameters of synchronous grouting slurry

3.2 结果验证

针对Sophia 铁路盾构隧道，将相关参数代入同步注浆整体扩散模型的数值计算程序中，得到注浆压力沿管片外壁的分布结果。需要说明的是，浆液在盾尾间隙中填充扩散时，由于刀盘超挖、地层收敛等因素导致盾尾间隙厚度分布不均，此外浆液在与土体的交界面处还会发生泌水、渗流等过程，土体对浆液的阻滞作用与浆液在一般内壁平整的管道中流动时受到的阻滞作用相比复杂得多。因此，盾尾间隙厚度计算参数不宜直接选择盾尾间隙理论值，应当进行折减以考虑地层交界面对浆液流动的复杂阻滞作用。文献［4］浆液压力监测数据显示盾尾注浆影响范围在出盾尾2～3 环内，对应的折减系数可取为50%。

根据表1 所述的注浆压力和环境压力值，计算试验横截面处的浆液压力分布，并同现场实测数据进行比较，如图10所示。

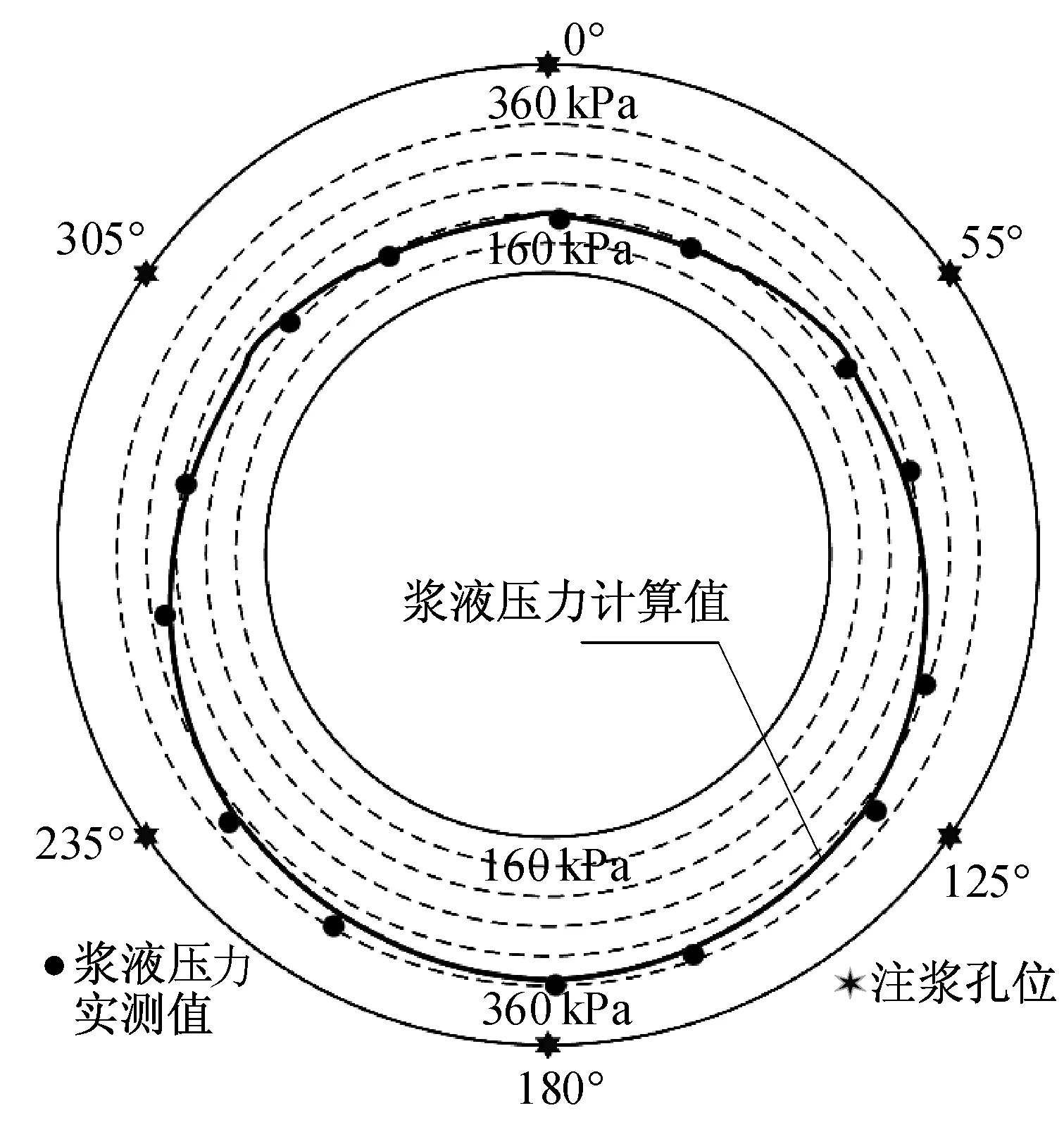
图10 计算值与实测值对比Fig.10 Comparison between calculated and field values

由图10 可见，隧道拱顶的浆液压力实测值为200 kPa，拱底压力实测值为353 kPa，浆液压力受浆液自重影响明显。浆液压力实测值分布在理论计算值两侧，整体上具有较高的吻合度，同步注浆整体扩散理论模型能够较好地反映浆液在盾尾间隙充填过程中的压力分布模式。

3.3 结果分析

文献［8］中提出的同步注浆充填压力环向分布模型假定浆液沿着三维环状薄饼扩散，但环状薄饼空间只是理想化的假定，实际盾构注浆过程中盾尾间隙内并不会出现类似的空间，其厚度参数既没有经验取值，也没有相关试验研究，取值缺乏依据。而且薄饼厚度参数δ 敏感性极强，对计算结果影响很大。图11为文献［8］提出的环向分布模型与本文纵环向整体扩散模型的计算结果对比。当环向分布模型的δ 取值为1.5 和3.0 cm 时，计算结果的最大误差分别为－12.64%与6.93%，而本文的整体扩散模型则为5.28%。此外，以均方误差（mean-square error，MSE）作为计算结果偏差程度的评价指标，三条曲线对应的MSE 分别为398.94（环向分布模型δ=1.5 cm）、196.49（环向分布模型δ=3.0 cm）和69.40（整体扩散模型）。可以看出，环向分布模型的准确性十分依赖δ的正确取值，取值不同，计算结果曲线差异很大。因此，薄饼厚度参数δ 成为了制约环向分布模型应用的因素。而整体扩散模型假设条件较少，不存在薄饼厚度参数δ，其更真实地反映浆液在间隙中的流淌规律，其计算结果也更加精确。

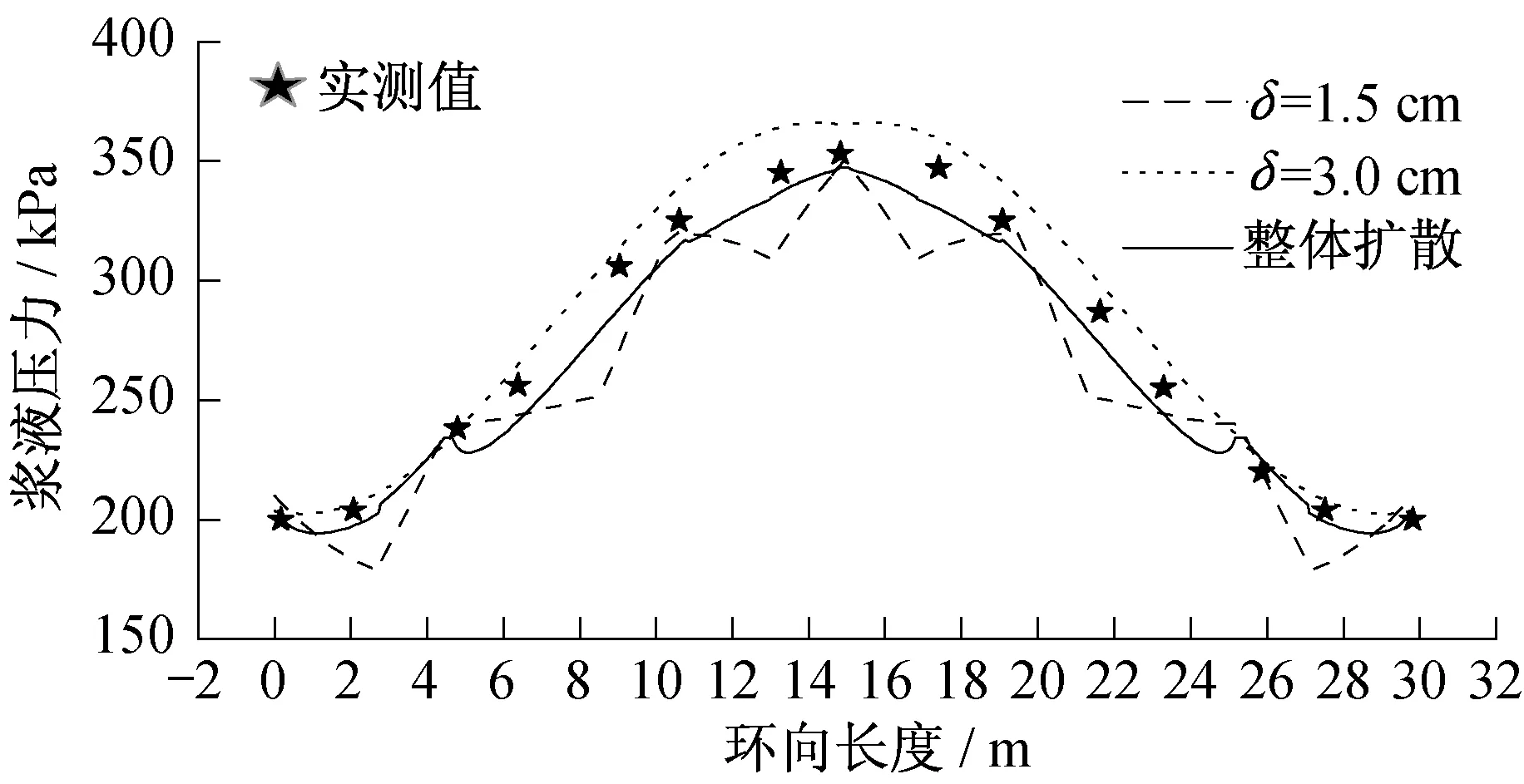
图11 不同模型计算结果对比图Fig. 11 Comparison of calculation results of different models

此外，同步注浆整体扩散模型的计算结果可以得到注浆范围内任一点的浆液压力。由于计算结果左右对称，本文仅取右半部分进行分析。图12分别为注浆孔1，2，3，4 同时注浆时的扩散压力展开云图，其中横坐标表示沿着管片外壁的弧长，其值为0表示隧道顶部，数值随着顺时针旋转增大，其值为14.92 m表示隧道底部；纵坐标表示沿着隧道轴线的距离，其值为0 表示盾尾所在横截面，距离盾尾越远，数值越大；云图表示浆液压力的分布情况，单位为kPa；图中横轴上的圆环表示注浆孔位置。从图中可以看出，隧道顶部和底部区域由于管片外壁较为平坦，重力影响不明显，浆液压力变化幅度较小，而且由于浆液粘滞阻力的影响，距离注浆孔较远范围内浆液压力小于注浆压力值；而在拱肩和拱腰处，管片外壁切线与竖向夹角较小，重力对浆液压力的变化起控制作用，因此等高线在距离注浆孔一定距离后几乎与隧道轴向平行。

图12 注浆孔单孔扩散压力分布云图Fig.12 Contour of diffusion pressure for single grouting

基于不同注浆孔注入的浆液在交汇面处浆液压力相等的原则，对4个注浆孔的计算结果进行整合，得到整个管片外壁右半部的浆液扩散压力分布展开云图，如图13所示。将浆液扩散压力投射到半圆柱形管片外壁，可以直观地观察到浆液扩散压力的起伏情况，如图14所示。从图14可以看出，拱顶部位，浆液压力由于粘滞阻力的影响，出现明显的下凹区，而注浆孔附近会出现一定范围的上凸区。网格的颜色也体现了浆液压力的相对大小，结合图13，可以看出注浆压力整体上呈现着上小下大重力主导的趋势，竖向梯度约为16 kPa·m-1，而在注浆孔附近局部区域浆液压力分布较为复杂，与注浆孔位置，浆液流动方向以及注浆压力与环境压力之间的压力差等因素有关。在盾构正常推进过程中，注浆孔在未发生堵塞时，注浆压力只会略高于外界环境压力。因此，浆液压力的整体竖向梯度与3.1节中的环境压力的分布梯度会近似一致。

图13 同步注浆整体扩散展开云图Fig.13 Contour of overall diffusion pressure

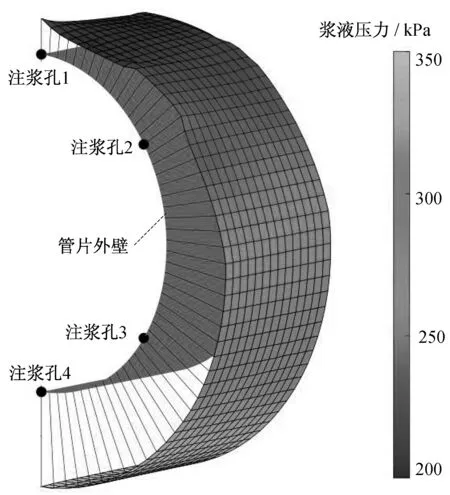
图14 浆液压力立体网格云图Fig.14 Stereoscopic mesh and contour of grout pressure

图15 为注浆孔处浆液沿着隧道轴线纵向扩散时的压力衰减曲线，可以看出在距离注浆孔较近区域内，压力衰减速度较快，而距离注浆孔一定范围内，压力趋于平缓。呈现这种压力衰减规律的原因是因为浆液由注浆孔注入后，浆液的流动速度较大，因此受到的粘滞阻力也比较明显，随着浆液的后续扩散，浆液的流动速度逐渐减小，压力衰减的梯度也随着减缓。

图15 浆液压力纵向扩散衰减曲线Fig.15 Longitudinal diffusion attenuation curve of slurry pressure

4 结论

本文通过分析盾尾同步注浆填充扩散机理，改进了现有的盾尾同步注浆扩散模型中浆液纵、环向流动相互独立的假设条件，将浆液的扩散视为纵环向相互关联的流动模式。此外，盾尾同步注浆施工通常以注浆量或注浆压力作为控制参数。但注浆量控制更多地被认为是一种二次被动反馈控制方式，在盾构机转弯和升降阶段中超欠挖时或者遇到复杂地质情况时（诸如裂隙分布较多，存在岩溶空洞），往往无法有效填满建筑空隙。而注浆压力控制能更好地适应周围土层环境压力的变化，实时调节盾尾注浆流量，减小地层扰动和环境影响。因此，本文以注浆压力为同步注浆控制参数，通过理论推导和数值算法设计得到了盾构隧道同步注浆纵环向整体扩散理论模型和计算程序，并进行了工程实例分析，得到结论如下：

（1）基于Bingham流体本构模型，考虑浆液纵环向关联整体扩散运动，以注浆压力为控制参数，环境压力为边界条件，得到了盾尾同步注浆浆液压力空间分布理论模型。

（2）以压力为边界条件，考虑重力影响，浆液在盾尾间隙内的扩散范围以及扩散锋面形态为不规则环状。基于时空离散的概念，对扩散区域进行离散化，通过构造离散网格节点的平衡方程组，求解注浆压力与浆液扩散半径（浆液扩散锋面）的关系式，进而建立了求解盾尾同步注浆范围内任一点的浆液压力的数值算法。

（3）盾构隧道同步注浆纵环向整体扩散模型相较于环形分布模型，改进了假定条件，不需引入环饼厚度等敏感假定参数，更加贴近工程实际情况。

（4）工程实例分析表明浆液压力整体上呈现着上小下大重力主导的趋势，竖向梯度约为16 kPa·m-1，而在注浆孔附近局部区域浆液压力分布较为复杂，与注浆孔位置、浆液流动方向以及注浆压力与环境压力之间的压力差等因素有关。同步注浆整体扩散理论模型能够较好地反映浆液在盾尾间隙充填过程中的压力分布模式。