近红外偏振无关超透镜研究
2020-06-16蒲欣欣肖相国朱业传刘卫国
蒲欣欣,周 顺,肖相国,朱业传,程 进,刘卫国
(1. 西安工业大学 光电工程学院,陕西 西安 710021;2. 西安应用光学研究所,陕西 西安 710065)
引言
作为聚焦与成像器件,透镜及其光学系统在显微成像、深空探测、微纳制造等诸多技术中具有广泛应用,同时也是对地观测国家重大专项等诸多领域的核心器件。然而,传统折射式透镜因为体积大、质量重、曲面加工困难、难以突破衍射极限等缺陷,不适用于先进成像系统微型化、轻量化、集成化、高分辨率等发展需求。利用微纳结构对光的调控成为国际上竞相发展的前沿技术,基于微纳结构的超薄平面透镜为解决传统透镜存在的难题提供了一种全新的实现方案[1]。由许多亚波长结构单元按照一定功能排列的超表面则很好地弥补了传统透镜的不足,通过对光波振幅、相位及偏振的精准调控,可实现多种光学功能,如光学聚焦、异常反射[2]等。根据结构、材料、设计思想的不同,超表面可以被分为不同的类别,但不同超表面对光束的调控本质是一样的[3-4],通过改变微结构的几何参数获得不同的光学响应,再根据所需相位进行排列便可以实现电磁波的调控。超表面优异的光学性能和超强的波前调控能力,使得各种超薄器件得到了更广泛的发展,在成像、显微术和光谱学领域中展现出独特的优势,现已成为研究最广泛的高集成、微型化光学元件之一[5-6]。
国内外对不同波段下的超表面具有广泛的研究,在可见光波段,斯坦福大学通过改变天线的旋转角度控制圆偏振光的相位,实现了半波片、透镜等光学器件功能。在该波段下受到偏振片的影响,光束强度与第一级衍射级相比非常低[7]。Capasso课题组设计了高性能超表面透镜,透镜由二氧化钛介质棒和玻璃基底组成,解决了可见光频段材料的选择问题,但由于受到几何相位调控的限制必须使用圆偏振入射光[8]。针对近红外波段,2018 年,Gianluca Ruffato 基于几何相位,在1.31 μm工作波长下设计了基底和相位调控单元都为硅的硅矩形超透镜,基底具有较大反射率,导致能量损失严重[9]。武汉大学的郑国兴团队、东南大学崔一平小组等利用几何相位实现了不同波长下的聚焦[10],但几何型相位超表面器件受到光束偏振态的限制,单元结构的几何参数只在某一特定偏振方向发生变化,相位调控单元也只在该偏振光作用下产生对应的相位延迟,偏振片的加入导致入射光能量被削减,能量损失较大,因此器件的能量利用率较低[11-13]。
本文为解决在引入超透镜设计时偏振片会导致能量损失和器件整体利用率低下这一问题,由于圆柱形单元结构不具有手性,因此相同的单元结构所产生的的传输相位不受偏振方向的影响,具有偏振无关性。基于此特性,在近红外1.31 μm工作波长下,构建了一种硅圆柱调控单元。通过 时 域 有 限 差 分 法(finite-difference time-domain,FDTD)仿真了不同硅圆柱半径、不同周期的相位延迟,得到了能够完整覆盖一个周期的硅圆柱直径范围、周期大小对透过率的影响以及周期和波长的关系,基于仿真优化的单元结构完成圆形超透镜的设计,实现聚焦功能。在解决偏振片导致效率低下问题的同时,针对大部分成像目标都是偏振无关的,所设计的偏振无关超透镜在近红外成像领域中具有广阔的应用前景,如近红外摄像仪。
1 相位调控单元设计
光波的3 个基本物理参量是实现电磁波调控的关键,实现对这些物理参量的精准控制,就可以实现对光束的灵活操控,获得所需的功能[14-16],所构建的超表面单元结构如图1 所示。整个单元结构由两层构成,选择具有高透过率、低折射率的SiO2材料作为基底,高折射率、低吸收率的Si 作为相位调控单元,其中P 为单元结构周期,h 为调控单元高度,d 为调控单元直径。
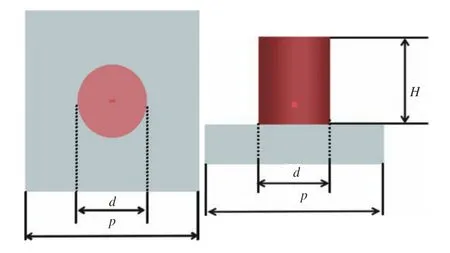
图 1 超表面单元结构示意图Fi g. 1 Schematic diagram of metasurface unit structure
利用FDTD 对所构建的相位调控单元进行分析。相位随着调控单元高度H、直径d 以及单元结构周期P 的变化而变化,在调控单元高度h 和周期P 不变的情况下,通过改变调控单元直径达到调控的目的。直径越大,相位延迟越大;反之,相位延迟越小。获得不同直径硅圆柱的相位延迟差分布图,创建相位延迟差关于半径的拟合函数。
超表面的不同位置处所存在的微结构参数不同,当光波经过相位调控单元,不同位置处的相位延迟也不相同,从而引起出射光波阵面的改变,使入射光经该平面后具有会聚功能。平面微结构所造成的相位延迟差 ∆φ应满足波前重构方程,公式如下:
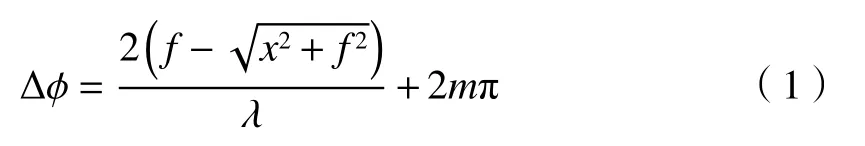
式中: f 为焦距; x为 位置坐标; λ为工作波长。通过理论计算得到的相位延迟差和每一位置处硅圆柱直径相匹配,通过对不同直径的硅圆柱进行排列,使出射光在所设计的焦距处实现聚焦功能。
2 相位延迟分析
硅圆柱相位调控单元的半径r、高度H、单元结构周期P 是3 个影响相位延迟和透过率的基本参数,本文研究了不同参数条件下的相位延迟分布。通过FDTD 进行仿真计算,对单元结构参数进行优化,得到可完整覆盖一个周期的直径范围、高度H 和周期P,验证了所设计的单元结构对相位可进行精准调控。
2.1 调控单元半径r 对相位延迟的影响
在相位调控单元高度H 为0.9 μm、单元结构周期为0.5 μm 的条件下,改变硅圆柱半径,得到不同直径所对应的相位延迟分布差,如表1 所示。

表 1 不同硅圆柱半径对应的相位延迟差Table 1 Phase delay difference corresponding to different radius of silicon cylinder
表1 所示的是不同直径硅圆柱所对应的相位延迟差大小,当硅圆柱半径为0.1 μm~0.22 μm,相位延迟差实现了0~2π 的相位覆盖,说明相位调控单元直径的变化可对光波进行有效调控,确定了相位调控单元的取值范围,该硅圆柱半径所对应的相位延迟差分布图如图2 所示。
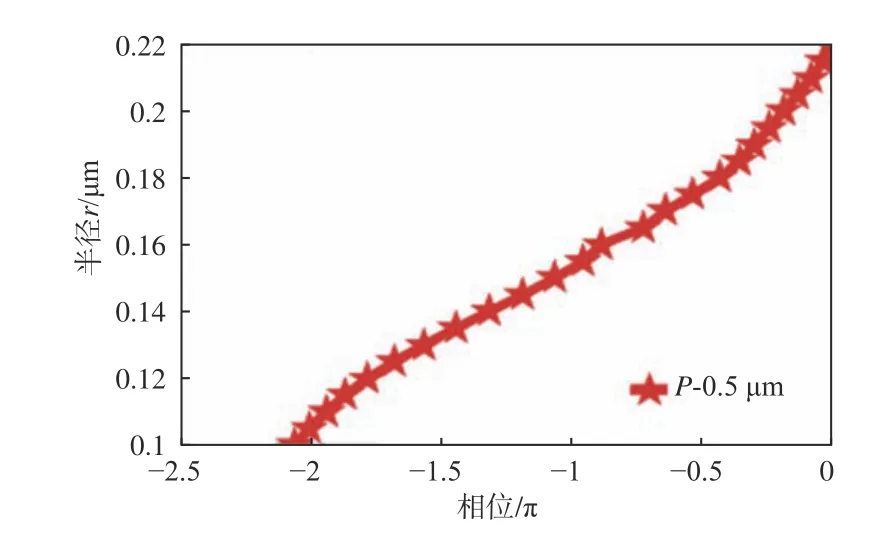
图 2 不同半径对应的相位延迟差分布图Fig. 2 Distribution of phase delay difference corresponding to different radius
如图2 所示,横坐标为相位延迟大小,纵坐标为硅圆柱半径,随着半径r 的变化,相位也发生着变化,在所设计的半径范围内,相位延迟完整覆盖了一个周期。单元结构周期、高度任意一个发生改变都会使相位延迟发生变化,相位延迟随着硅圆柱高度的增大而增大,当硅圆柱直径改变时,有效折射率的变化引起所对应相位发生变化,从而使不同直径的硅圆柱相位延迟不同。硅圆柱高度的增大会使单元结构的深宽比增大,从而增加加工难度,同时,硅圆柱高度越大,所设计的单元结构的失效点也会增多,使该直径所对应的相位调控单元失去相位调控的能力,无法实现完整周期的相位调控。
2.2 调控单元高度H 对相位延迟的影响
相位调控单元的硅圆柱半径r 为0.1 μm~0.22 μm、单元结构周期P 为0.5 μm 的条件下,选取硅圆柱高度为0.8 μm、0.85 μm 和0.9 μm 这3 组数据进行仿真,得到不同高度所对应的相位延迟分布,如表2 所示。

表 2 不同高度对应的相位延迟差Table 2 Phase delay difference corresponding to different heights
从表2 可以看出,为获得完整的相位延迟覆盖,在硅圆柱半径r、单元结构周期P 一定的条件下,适当地增加硅圆柱高度,达到可实现0~2π 完整周期相位覆盖的目的。改变硅圆柱的高度可以对相位进行调控,不同的高度值对应不同的相位延迟,但考虑到加工问题,高度的变化会增加加工难度,不利于器件的批量化生产。将高度作为恒定值,只通过硅圆柱半径r 改变来调控相位,对3 组硅圆柱高度所得到的相位分布进行对比分析,选择0.9 μm 作为最优的高度值。
2.3 单元结构周期P 对相位延迟和透过率的影响
为保证超透镜具有良好的透过率和聚焦效果,研究了不同周期对相位延迟和透过率的影响。在硅圆柱高度H 和半径r 保持不变的情况下,选取单元结构周期分别为0.8 μm、0.6 μm、0.5 μm,3 组不同周期条件下的相位延迟分布如图3 所示。
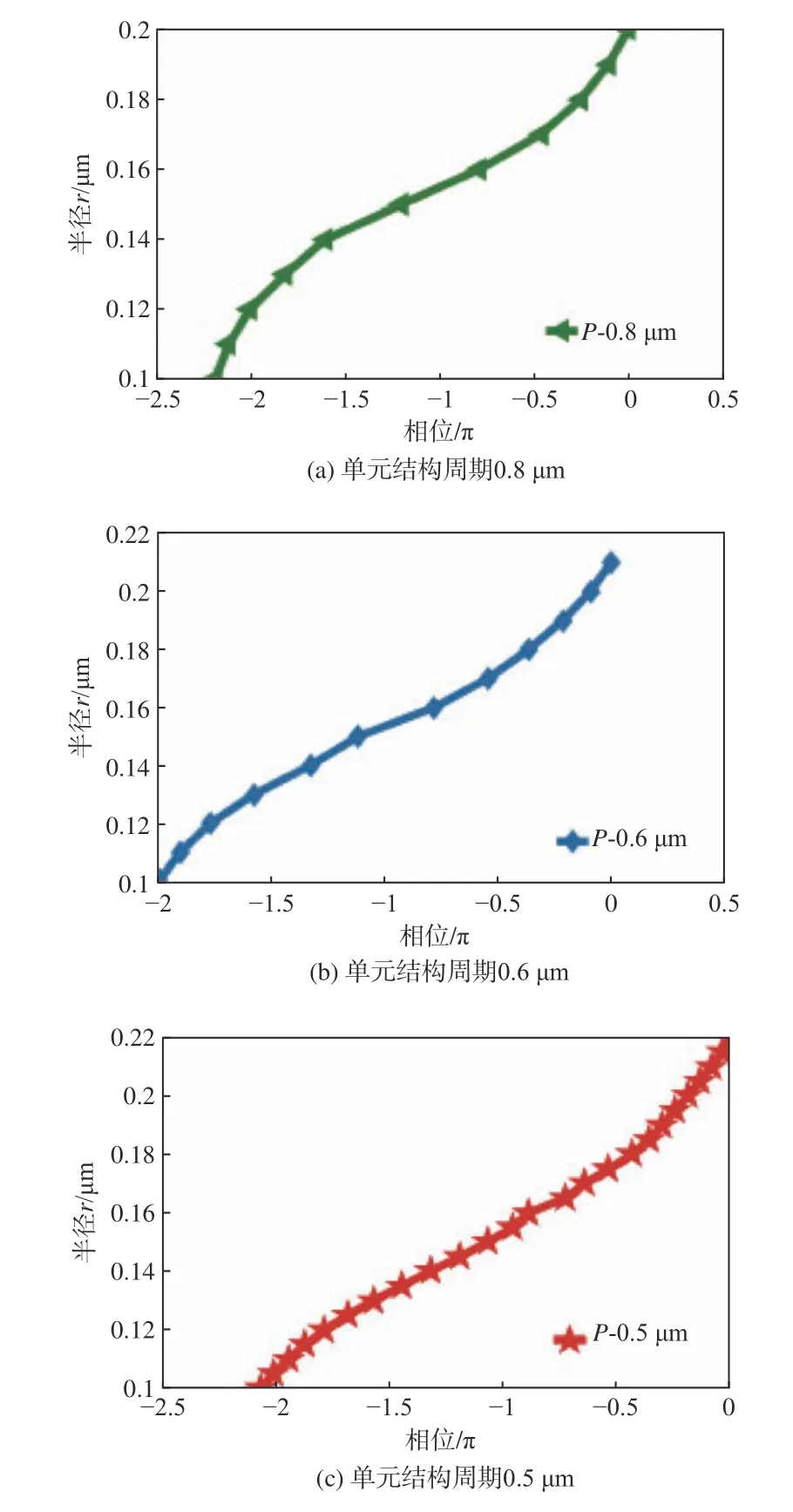
图 3 不同周期对应的相位延迟差分布Fig. 3 Distribution of phase delay difference corresponding to different periods
由图3 可以看出,相位延迟差随着硅圆柱半径的增大而增大,且都实现了0~2π 的相位覆盖,但是不同周期所对应的硅圆柱半径范围不同,周期的减小导致硅圆柱半径取值范围增大。图3 中曲线出现了不平滑节点,这是由于当周期为定值时,2 个硅圆柱之间的距离会影响硅圆柱的相位延迟,当相邻硅圆柱之间的距离过大时,光波进入微结构会直接融空隙中透射,使硅圆柱无法进行相位调控。当相邻硅圆柱之间的距离过小时,易受到光场之间的相互作用,无法获得所需要的相位延迟,最终影响超透镜的聚焦效果和透镜整体的透过率。因此,根据不同单元结构周期所形成的超透镜的透过率来选择合适的周期大小,在保证良好透过率的前提下得到最优周期值。
表3 所示为根据时域有限差分法计算得到的几组不同周期对应的透过率大小及波长和周期的比值。通过3 组数据的对比可以发现,在深宽比和完整周期相位调控的条件下,单元结构的周期越小,超透镜的整体透过率越高。超透镜工作波长不同,周期的大小也不一样,当单元结构过大,接近于一个波长的时候,入射光将直接从硅圆柱之间出射,所设计的硅圆柱结构失去相位调控的能力,无法对光波进行调控改变其出射光波前。当波长和周期的比值越大时,单元结构周期越小,所选取的硅圆柱直径也越小,只能通过增加硅圆柱的高度达到一个完整周期的相位调控,过大的高度值和较小的硅圆柱直径使得深宽比增大,加工工艺受到限制。

表 3 不同周期对应的透过率Table 3 Transmittance corresponding to different periods
3 透镜设计及聚焦性能
通过对硅圆柱半径、高度和单元结构周期的优化,得到硅圆柱单元结构的最优参数值,基于最终的优化参数对半径r 和相位延迟差进行拟合,如图4 所示。图4 中黄色、绿色、紫色3 条曲线分别为对相位延迟差进行二次、三次、四次拟合得到的半径r 关于相位延迟差的拟合方程。通过对比,选择四次拟合的结果作为最优拟合参数,拟合方程为

图 4 相位延迟差关于半径r 的拟合曲线Fig. 4 Fitting curve of phase delay difference with respect to radius r
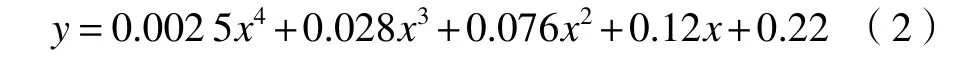
根据(2)式可计算得到相位延迟差所对应的硅圆柱半径r,其中y 为硅圆柱的半径,x 为理论计算的相位延迟差。对硅圆柱半径和相位延迟差进行分析,结合公式(1)得到每一位置处所需相位延迟差的大小和半径,从而完成超透镜的设计。
所设计的超透镜整体示意图如图5 所示。透镜半径为10 μm,焦距为20 μm,对半径不同的硅圆柱进行排列,获得实现聚焦功能所需要的微结构阵列。当平面波垂直入射至基底,经过微结构后发现出射光在19 μm 处发生了会聚现象,如图5 所示。
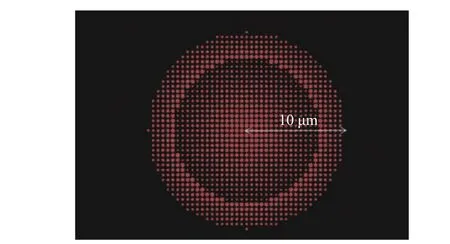
图 5 超透镜整体示意图Fig. 5 Overall schematic diagram of metalens
图6 为模拟圆形超透镜的聚焦示意图。图6(a)为XZ 面的光场分布情况,可以看到所设计的超透镜实现了聚焦,焦距为19 μm,与设计的焦距未完全匹配,这是因为相邻柱子之间耦合作用导致焦移现象发生。图6(b)为XY 面的光场分布情况,入射光经过硅圆柱结构后会聚到一点,实现了聚焦功能,焦点半高宽FWHM=1.4,超透镜的整体透过率达到65%。由图6 可以看出所设计的单元结构不受偏振光的影响,极大地增加了器件的利用率。
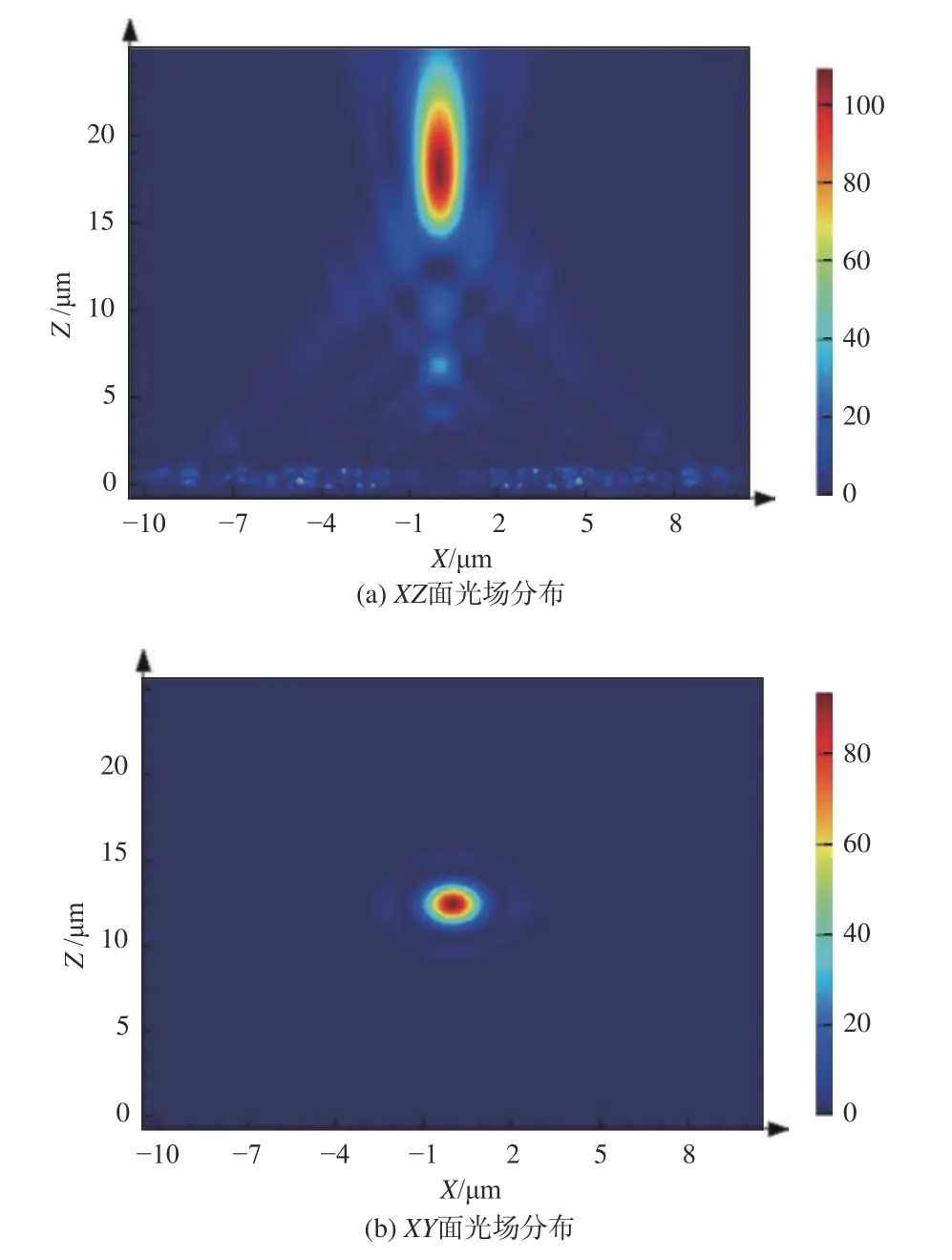
图 6 仿真聚焦示意图Fig. 6 Schematic diagram of simulation focusing
4 结论
基于有效折射率理论,利用圆柱形单元结构对偏振不敏感,设计了一种偏振无关的硅圆柱超透镜,其工作波长为近红外1.31 μm,通过仿真计算,对硅圆柱半径、高度和单元结构周期进行了优化。从仿真结果可以看出,在不考虑偏振光的情况下,所设计的单元结构实现了光波的有效调控,对于垂直入射的平面波,硅圆柱单元组成的超表面结构在透射场中实现聚焦,且透过率达到65%。本文所设计的偏振无关超透镜不仅实现了光的会聚,而且不受偏振态的影响,使器件的利用效率有所提高。根据所设计的器件的工作波长,其在精细激光束、激光雷达以及激光夜视仪等领域也具有重要应用。
