采用分区法生成稀疏谱湍流相位屏

张小琪，倪小龙，刘 智，丛明慧，张 洁

（长春理工大学 电子信息工程学院，吉林 长春 130022）

引言

空气因地面和太阳辅热向上流动，在这个过程中受风速和大气分子运动影响形成大气湍流。大气湍流引起大气折射率的改变，从而导致光束波前发生畸变，引起光斑闪烁、光斑漂移等效应[1]。在空间激光通信研究方向中，要减小误码率保证通信双方通信质量，必须对激光在大气湍流中的传播特性进行研究，以寻求抑制大气湍流效应的方法，所以需要找寻室内可替代的实验环境模拟大气湍流以便进行光通信研究。

现代光学采用数值模拟方法模拟大气湍流的真实状态[2]，常用的器件是液晶空间光调制器（LCSLM）。近些年提出的稀疏谱模型具有细节信息丰富、模拟周期长的优点，在稀疏谱模型下，二维随机场的精确要求达到5 个数量级以上的尺度变化，需要长的湍流相位屏来表示波前的时间演变。相位屏模拟常用方法有功率谱反演法、泽尼克法和次谐波法等[3]，这些方法能够较好地模拟大气湍流的特性，但也存在计算量大、模拟速度比较慢、具有周期性等问题，优化过程十分复杂，往往需要多种方法叠加，导致计算量成倍增加[4]。稀疏谱湍流相位屏应该具有较长的周期，采用上述经典模拟方法的方法是不可行的，因而本文考虑采用一种稀疏谱分区模型得到符合要求的湍流带[5]。

1 稀疏谱基本理论及其相位屏生成方法

稀疏谱的概念最早提出是用于海面模型的研究，后来推演到大气湍流相位屏的研究。稀疏谱模型认为每个随机场的实现都包含有限个随机正弦波分量，其中频率、相位和幅度都是随机的。光谱分量的数量由湍流状态决定，而不是由所需的空间分辨率和湍流尺度决定[5]。

1.1 稀疏谱基本理论

本文采用的稀疏谱模型和传统的大气湍流理论模型一样，相位屏结构函数服从湍流幂律形式：

式中： r0是 相干半径； a为光谱指数。一般认为结构函数和相位波动的空间谱有关，则结构函数可以表示为

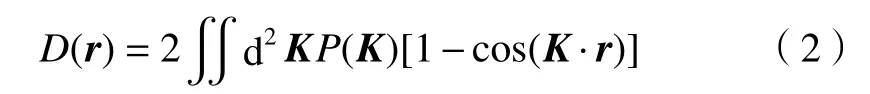
其中 K为波矢，可从波长K 和方向两个方面考虑，其中谱密度可以近似表示为

关于 P(K)，引入归一化结构函数d(y) 和无量纲变量 y=k0r 进行分析，其中： k0=L/2π,K0=l/2π，归一化结构函数可以表示为

稀疏谱模型采用介于内外尺度的幂律函数拟合归一化结构函数，图1 是惯性区内归一化幂律结构函数和归一化结构函数曲线对比图，其中横坐标表示无量纲变量y，纵坐标表示归一化结构函数和幂律结构函数的值。

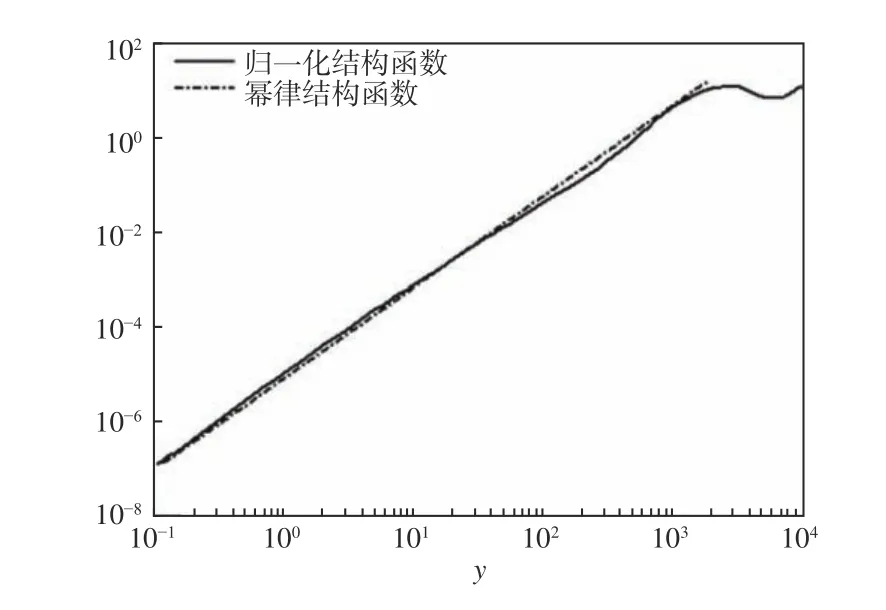
图 1 幂律函数和归一化结构函数Fig. 1 Power law function and normalized structure function

由图1 可见，在K0＜K＜k0时，幂律函数能够很好地拟合归一化结构函数，则

所以公式3 的表述形式是合理的。

1.2 稀疏谱模型下的相位屏模拟方法

稀疏谱模型舍弃了和湍流扰动无关的信息，保留了细节信息。稀疏谱模型能够表示为具有离散随机特点的三角级数形式，通过蒙特卡罗方法计算模拟随机场特性的过程能够减少计算量，产生较长周期的相位数据且保留与大气湍流扰动相关的尺度参数。以功率谱反演法为例，需要先进行傅里叶变换，引入相位畸变后，再作傅里叶反变换得到我们需要的相位屏[6]，这个过程计算量巨大，且需要进行时频域变换。本文不采用经典相位屏模拟方法，避免时频域的变换，从数学分析入手，简化计算过程减小计算量。

类似于传统的傅里叶模型，相位可以表示为

式中：An为是符合随机正态分布的复振幅； Kn是具有均匀概率分布的随机波矢量。由(1)式，稀疏谱模型的结构函数可以表示为

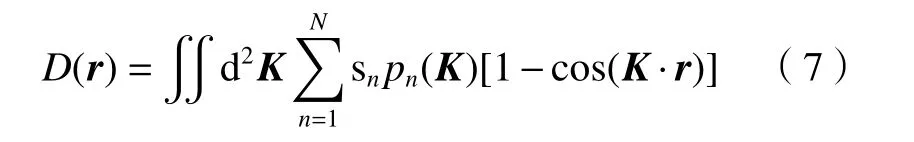
则（7）式要符合（1）式幂律形式的结构函数需要满足：

假设波矢方向服从[-π,π]上均匀分布，且符合相位的统计各向同性，则

其中 φ表示波矢的方向。那么，（8）式可以表示为

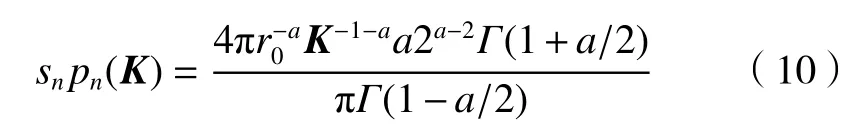
为了减小计算量且使相位屏的周期性尽可能地大，从数学角度出发，采用对数分区的方法对频谱范围[K0,k0]进行分区，将该区间分成N 个子区间：

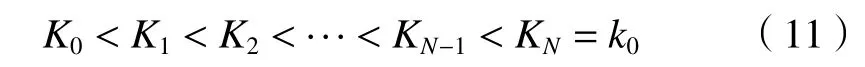
并且要求仅在第n 个区间上支持概率分布 pn(K)。第n 个区间的的频谱可以表示为

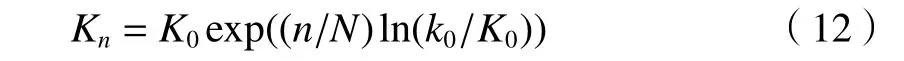
在第n 个子区间上权重为

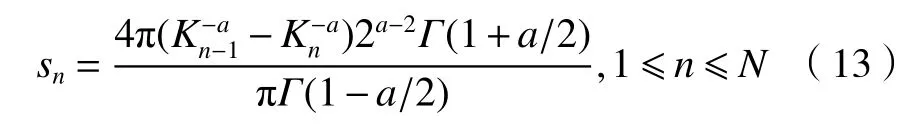
由（10）式和（13）式可以得到第n 区间的波数为

其中ξ 是[0，1]均匀分布的随机数。在这里引入随机数会导致相位的改变，从而导致整个相位屏上的点发生不同程度的相位畸变，以达到模拟大气湍流的效果。

对比使用最多的功率谱反演法，采用这种简单的数学分区方法，计算过程简化了许多，由于实验所需采样点数较多，能够大大减小计算量，因而稀疏谱分区模型具有明显的计算量优势。简单的形式变化和近似替代，而没有时频域的变化，也就避免了傅里叶变化的周期性，所以分区方法能有效保留稀疏谱模型的无限周期性。

2 相位屏数值模拟

2.1 湍流母屏的选择

图2 是大气湍流模拟的理论装置图和实物图。光束的传播路径大致为：激光器发射的红外激光束通过偏振片经分光棱镜进入LC-SLM，电脑将已经编译完成的相位屏信息加载到LC-SLM 的硅板上，LC-SLM 通过电寻址方式使液晶分子发生偏转，从而使光束发生相位畸变。LC-SLM 将光束反射回分光棱镜，最后由相机收集光斑[7]，对光斑的采集可参考文献[8]。

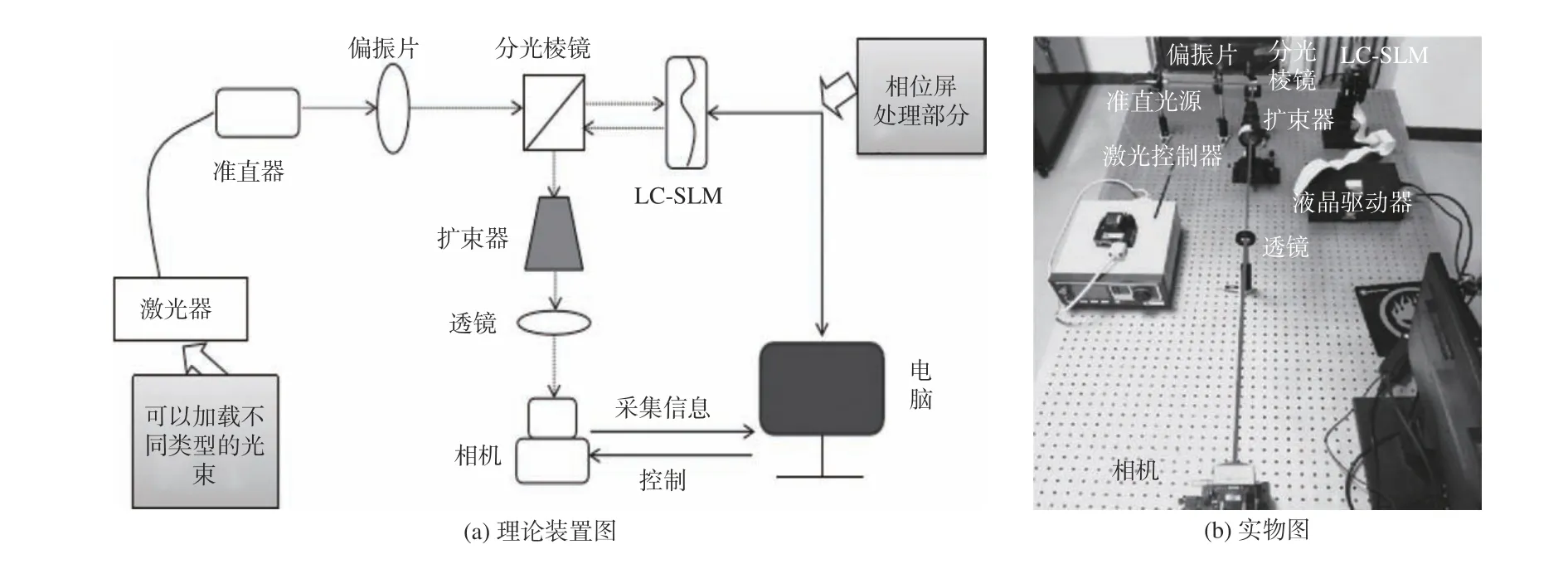
图 2 基于稀疏谱的大气湍流模拟装置Fig. 2 Atmospheric turbulence simulation device based on sparse spectrum

相位屏模拟分为动态模拟和静态模拟两种[9]，现在很少用到静态相位屏法。本文采用动态相位模拟法，即根据风速从一个较大的母相位屏中连续截取出子相位屏，这些子相位屏构成动态相位屏[10]。图3 是动态螺旋状和往复型截取相位屏的示意图，本实验以功率谱反演法旋转截取子相位屏作为对比组实验，因为湍流母屏大小的限制且母屏的生成具有周期性，谱反演方法往往需要作出补偿来弥补这些不足，这个过程计算量十分巨大。

稀疏谱模型理论上可以得到一个非周期性样本，考虑取x 轴远大于y 轴。本实验基于相同的幅度和波矢，生成长带形的湍流相位屏，按照风速方向截取子相位屏并依次加载在液晶上，子相位屏的连续加载形成了动态的湍流模拟效果，如图4所示效果（取部分湍流带）。本实验母相位屏采样点数为512×32 768，取子相位屏分辨率为512×512像素。

图 3 传统子相位屏截取示意图Fig. 3 Schematic diagram of traditional sub-phase screen capture

图 4 长带形湍流相位屏截取子屏示意图Fig. 4 Schematic diagram of sub-screen capture of long strip turbulence phase screen

2.2 稀疏谱相位屏结果分析

图5 是稀疏谱模型下生成的大气湍流相位屏。

图6～图8 分别取相干半径为0.01 m、0.05 m、0.1 m 时稀疏谱分区法生成的相位屏和功率谱反演方法生成的相位屏对比图。由灰度图湍流的密度可以看出在相同相干长度下，稀疏谱分区模型下的相位屏更加清晰，细节信息更加丰富，符合稀疏谱模型的特点，同时这也是稀疏谱模型明显的优点。观察两种情况生成的相位屏，均符合相干长度越小，湍流扰动越强烈的规律，由此，我们可以判断本实验生成的相位屏能够大致符合大气湍流扰动规律。

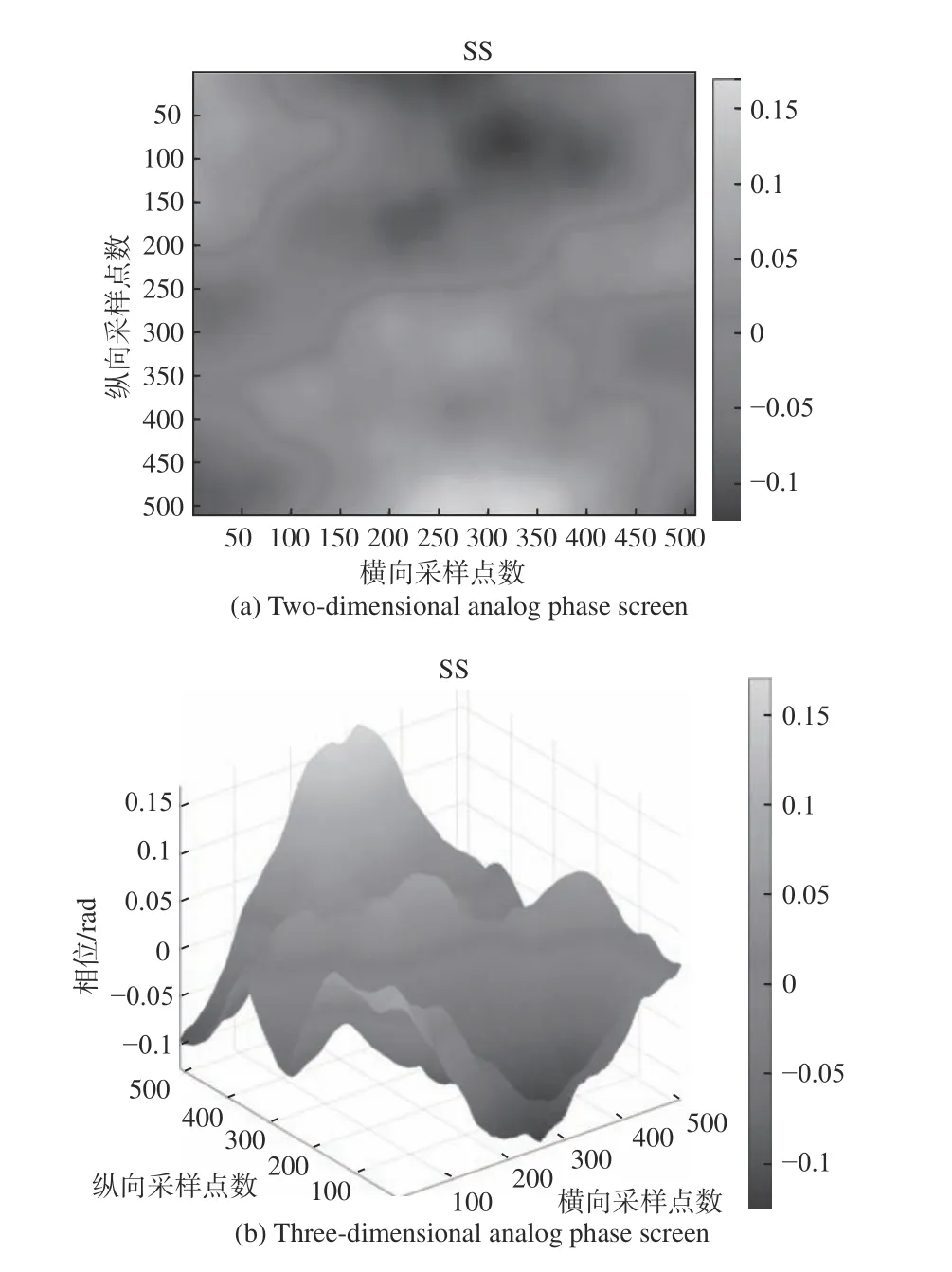
图 5 稀疏谱大气湍流相位屏Fig. 5 Sparse spectrum atmospheric turbulence phase screen

图 6 r0=0.01 m 时大气湍流模拟相位屏Fig. 6 Atmospheric turbulence simulation phase screen when r0=0.01 m

图 7 r0=0.05 m 时大气湍流模拟相位屏Fig. 7 Atmospheric turbulence simulation phase screen when r0=0.05 m

图 8 r0=0.1 m 时，大气湍流模拟相位屏Fig. 8 Atmospheric turbulence simulation phase screen when r0=0.1 m

图9 将采用稀疏谱分区方法和功率谱反演方法生成相位屏的结构函数和真实大气湍流的结构函数进行对比，根据相对误差判断本实验的大气湍流模拟效果。在计算结构函数时，参数均取经典值，相干半径取0.1 m，光谱指数取1.67，关于结构函数的生成方法，均选取相位屏左下角为相位屏半径的计算原点，一共选取500 个采样半径，计算每个采样半径下平均结构函数值作结构函数曲线。由湍流模型的标准结构函数得到理论结构函数曲线，并将理论结构函数和实际得到的结构函数做对比。对于计算误差，可以表示为

经计算，稀疏谱结构函数的平均误差为6.1%，理论上已经能够很好地模拟大气湍流[11]。由图9看出功率谱反演方法存在较大的低频补偿问题，一般采用次谐波法进行频率补偿或者是非均匀步长法[12-14]。而本文采用的稀疏谱相位屏模拟方法在数据量较大时依然能够较好地拟合相位结构函数，并且分区模型计算量大大减小。

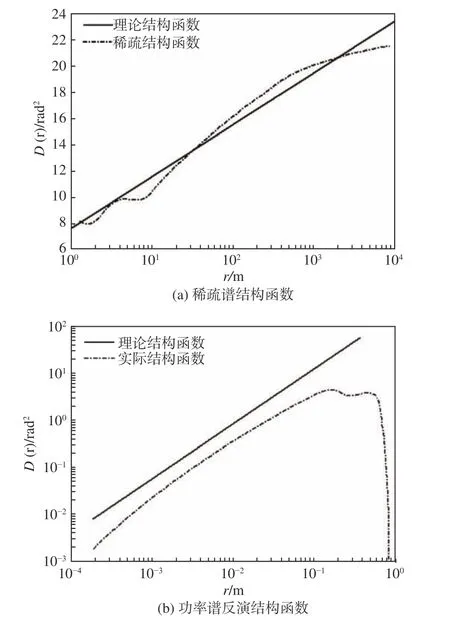
图 9 结构函数对比图Fig. 9 Comparison chart of structure function

光束经过大气湍流后其光斑位置会发生偏移，一般以光斑质心位置的变化来描述光束的偏移量，光束的漂移量是测量大气湍流传输特性的一个重要指标[15]。实验用230×230 个被采集点计算质心位置，质心位置x、y 轴方向计算公式：

其中I 表示光强，对于质心计算，取多幅光斑图片分别计算x、y 方向光斑中心位置，再对多个处理结果求平均值，最终将二维坐标作为光斑质心位置。以质心的偏差作为光束漂移量。

图10 为光斑质心位置的漂移量和真实大气湍流的光斑质心偏移量的对比图。r0为0.01 m、0.05 m、0.1 m 时，均方根误差分别为9.813×10−8m、9.951×10−8m、1.013×10−7m。由图10 可以看出随着大气相干半径的减小，大气湍流的扰动更加强烈，大气湍流光斑质心的均方根误差低至1.013×10−7m，所以稀疏谱模型下的大气湍流的光斑漂移情况基本吻合自由空间大气湍流的真实光斑偏移情况。

图 10 不同相干长度下的光束漂移量Fig. 10 Beam drifting distance at different coherence lengths

3 结论

本文重点研究了基于稀疏谱的大气湍流相位屏的生成方法，采用简单的数学方法分区方法生成相位屏，该方法不需要进行时频域的变换，避免了周期性问题，计算量明显小于经典方法，并且可以看出后期数据量较大时也不需要大量的补偿。利用LC-SLM 实现了对稀疏谱相位屏的加载并收集光斑信息。实验对比了稀疏谱分区方法生成的大气湍流相位屏和均匀功率谱反演法生成的大气湍流相位屏，容易看出，稀疏谱模型下的相位屏具有更加丰富的细节信息，并且湍流模拟效果更加清晰，随着相干长度的减小，湍流扰动也更加强烈。经验证，稀疏谱相位屏结构函数平均误差低至6.1%。将收集到的光斑和真实大气湍流条件下收集到光斑质心位置进行对比，光束偏移量的均方根误差为1.013×10−7m，符合实测大气湍流光斑位置变化规律。综上，本实验研究的稀疏谱分区方法生成的相位屏在理论和实践中都能够很好地模拟真实大气湍流。