空间外差光谱仪光谱降噪方法研究

王新强，张识翼，熊 伟，叶 松，王方原，李 树，李 莉

（1. 桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004；2. 中国科学院安徽光学精密机械研究所 通用光学定标与表征技术重点实验室，安徽 合肥 230031；3. 广西光电信息处理重点实验室，广西 桂林 541004）

引言

空间外差光谱仪（spatial heterodyne spectroscopy，SHS）是可搭载在遥感卫星上用于环境监测的仪器，2018 年我国在高分五号卫星上运用该仪器对大气污染气体进行监测[1]。该仪器具有超高分辨率、高光通量、实时探测等优势，因此得到科学家的高度重视[2-8]。小波分析是1974 年由法国科学家提出的一种处理非平稳信号的技术。目前大多数研究方向都运用第一代小波分析的原理，而小波系数的估计又为传统阈值函数。由于其缺陷性，在运用该算法进行处理时总得不到比较理想的信号。第二代小波变换是1995 年由Sweldens 提出用于实时信号处理等领域的技术。提升小波变换（lifting wavelet transform，LWT）因效率高、实时性强、信息损失小等优势，在信号处理领域得到了广泛应用[9-15]。本文在LWT 的基础上，对空间外差光谱信号进行降噪，分析其方法与传统的小波变换处理氙灯和积分球数据的影响。结果表明，该算法能更好地实现空间外差光谱降噪的目的。

1 空间外差光谱仪

空间外差光谱仪由光源、光阑、透镜、分束器、光栅和CCD 等构成（如图1 所示），它与迈克尔逊干涉仪最大的区别就在于将平面镜用闪耀光栅代替。首先入射光通过光阑A 进入透镜L1，透镜L1 把入射过来的光线准直后形成平行于光轴的光，然后经过入射波面进入到分束器上。分束器将入射光的反射和透射部分分别射向光栅G1和G2，其中2 个闪耀光栅与法线呈 θ角放置，2 束相干光经闪耀光栅衍射后再次射向分束器，然后以一定的夹角出射，最后合束在探测器上。当入射的光谱为 B(σ)时 ，干涉条纹 I(x)表达式为

式中：CCD 的像元大小和噪声分别为x 、 N(x)；系统基频波数为 σ；入射光波数为 σ0。从（1）式可知，SHS 捕获的 I(x) 与 B(σ)之间存在着傅里叶变换的关系。而在试验中，使用傅里叶变换的干涉图最终得到的是混杂着噪声的目标光谱。因此，实际空间外差光谱信号与真实空间外差光谱信号之间存在一定的误差，需要去噪。

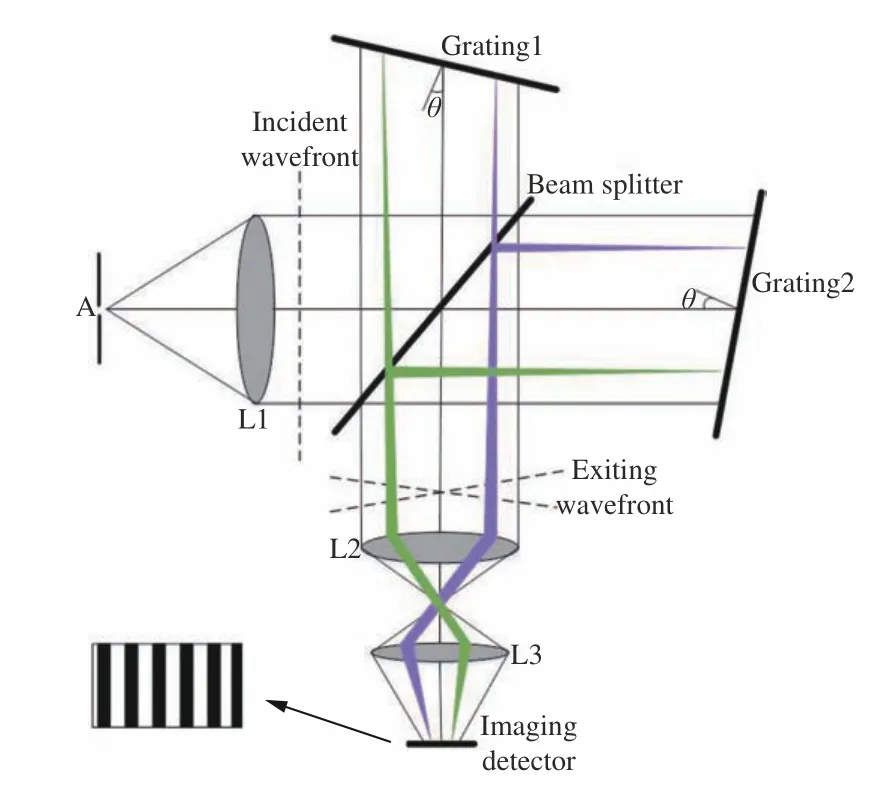
图 1 SHS 系统结构图Fig. 1 Structure diagram of SHS system

2 改进的提升小波变换分析

2.1 阈值的选取

噪声是随机出现在信号中的无规则波形，不能准确预测。对信号的每一层提升小波分解都采用相同的阈值，则可能会造成噪声滤除不彻底或信号损失的情况。因此提出一种根据不同层数而选择不同阈值的方法，数学表达式为

式中： Ti为第 i层的小波系数阈值；噪声的标准差为σi。估计噪声的标准差公式如下：

2.2 传统的小波变换

设信号为 f(t)， 小波系数为 φ(t)，则小波分析的数学式为

式中： φ∗为 φ(t)的 复共轭； a为 伸缩参量； b为平移参量。从（4）式可以看出，小波分析是基于傅里叶变换的，选定小波函数作为窗函数，通过时频拉缩和平移以达到小波匹配原始信号的目的。传统的方法用软硬阈值法来估计信号的小波系数。

硬阈值函数的表达式为

软阈值函数的表达式为

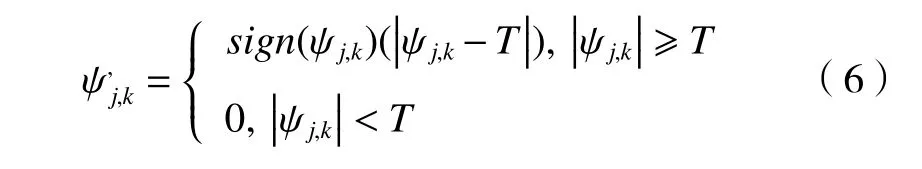
在（5）式和（6）式中，实际信号的小波系数和阈值分别由 ψj,k和 T表示。从以上数学表达式中可知：（5）式在阈值为±T 时不可导又不连续。其系数在±T时的不连续性会使信号在降噪时发生误差，造成振荡和伪吉布斯现象；虽然（6）式中的小波系数在函数域中处处连续，但在 ±T处依旧存在间断点。因此通过减小软阈值估计的小波系数使信号更为平滑，从而在一定程度上减少了振荡和伪吉布斯现象。但造成了实际信号与真实信号出现误差，这会使噪声去除更加不彻底和失去更多重要的细节特征，严重影响降噪效果。

2.3 提升小波变换

从以上结果可知，第一代小波分析是在傅里叶分析的基础上得到了改进，因而它也存在傅里叶带来的缺点。在空间外差光谱的反演过程中，需要利用傅里叶变换，这样会造成缺陷的叠加。相比较而言提升小波变换是不需要傅里叶分析进行构造的方法。它不仅在时域上实现小波变换且继承了小波变换的特性；可以根据实际需要来灵活地构建小波函数，实现信号与噪声的精准分离，避免了信号的损失；另外还采用整数的变换系数。 ai是第 i分解级别的近似系数，它分为3 个步骤。

1） 拆分

将 ai分为2 个不相交的子集。利用数据之间的关联性拆分为奇数索引据点（）和偶数索引数据点（），其中 k=1,2,···,length(ai)/2，即：

2） 预测（双提升）

3） 更新（原始提升）

针对小波变换阈值函数的缺点，在提升小波变换中运用一种双因子的阈值法来估计小波函数[16]。该阈值函数为

将LWT 分解并阈值处理的信号进行LWT 重构能突出细节特征和降噪，由于SHS 采集到的数据中含有各种复杂的噪声，因此需要把重构后的信号利用中值滤波来处理以弥补LWT 的不足。

3 数据处理与分析

3.1 干涉图和空间外差光谱

为了验证算法的有效性，使用了2 组不同仪器采集的数据。数据分别来自HEP-765-S 钾盐探测空间外差光谱仪：光谱范围为756.8 nm～771.7 nm，光谱分辨率为0.029 nm，图像像素为1 024×1 024，氙灯为光源；中科院自行研制的水汽探测空间外差光谱仪，光谱范围为930 nm～955 nm，光谱分辨率为0.05 nm，图像像素为1 024×1 024，积分球为光源，采集二维干涉图如图2 所示。

图 2 二维干涉图Fig. 2 Two-dimensional interferogram

分别任取一行干涉图，切趾、差分去基线、相位校正，然后作傅里叶变换，得到含有噪声的氙灯和积分球光谱曲线，如图3 所示。可以看出空间外差光谱信号中包含了明显的高频随机噪声，目标光谱的特征及重要的细节已无法进行有效识别。

3.2 分析改进LWT 降噪结果

图 3 FFT 变换光谱Fig. 3 FFT transform spectrum

图 4 氙灯降噪光谱Fig. 4 Xenon lamp denoising spectrum

分别运用了3 种算法对氙灯光谱信号进行处理，结果如图4 所示。图4（a）为小波变换软阈值算法处理效果，从图中可知该算法能抑制氙灯光谱曲线的噪声并使曲线平滑，但由于实际光谱信号与估计的光谱信号之间有误差，造成了信号过度平滑而丢失了重要的细节特征。另外由于实际氙灯信号线形相对简单，用硬阈值函数处理氙灯信号与软阈值结果基本一致，处理结果如图4（b）所示。相比小波算法，本算法由于结合了软、硬阈值函数优点，运用LWT 分解将信号更为精确地分为高、低频和科学的阈值选取等，既使得光谱信号中的噪声得到滤除，重要细节特征得到保留，也减少了因为传统处理方法处理造成的峰宽扩大。以实测低噪氙灯光谱信号为对比标准，如图4（c）所示，本算法结果图4（d）与其更为接近。

图5 为利用3 种算法处理后的积分球光谱信号。图5（a）为小波变换软阈值函数处理结果，从图中可以看出，因为实际的空间外差光谱信号与估计的光谱信号之间的不一致性，以及阈值函数间断点造成了噪声抑制不完全，出现较大尖峰噪声；而图5（b）硬阈值法处理效果比软阈值法好，信号被平滑却出现波形振荡现象；图5（d）为本文算法处理结果，从效果来看噪声被滤除且2 种小波变换阈值法都忽略的信号中重要细节特征在该算法得到了保留与突出，与图5（c）的实测积分球低噪光谱有较好的一致性。

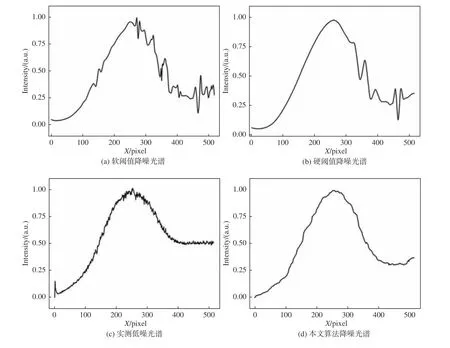
图 5 积分球降噪光谱Fig. 5 Integrating sphere denoising spectrum

3.3 性能分析

为了更为全面地说明该算法的可行性，从2 个定量指标方面分析处理结果，表达式如下：

式 中： f(n)为 理想 的空 间外 差 光 谱 信 号； s(n)为 降噪空间外差光谱信号； N 为空间外差光谱信号的长度。

从表1 和表2 的数据结果分析可知：硬阈值算法在信噪比（signal to noise ratio，SNR）和均方差（mean square error，MSE）方面都要比软阈值算法好，而本算法在降噪后最接近原光谱，同时在信噪比和均方差方面都要远远优于其他2 种算法。在氙灯处理过程中，本算法比软、硬阈值算法在SNR 上分别提高了24.6%和21.5%，MSE 分别减少了43.2%和40.2%；积分球处理过程中SNR 分别提高了31.0% 和30.6%，MSE 分别减少了51.5%和51.2%。因此本算法不仅能够滤除空间外差光谱信号中的噪声，提高信噪比，而且还能够保留和突出空间外差光谱信号中的细节特征。本程序进行多层分解和阈值选取等方法融合后运行速度还比小波变换阈值法快，因此，该算法比小波变换软、硬阈值方法更有效，更实用。

表 1 不同算法的降噪效果评价（氙灯）Table 1 Evaluation of denoising effects with different algorithms (Xenon lamp)

表 2 不同算法的降噪效果评价（积分球）Table 2 Evaluation of denoising effects with different algorithms (Integrating sphere)

4 结论

空间外差光谱技术是近年来发展起来的主要应用于卫星遥感和大气观测领域的新型超分辨技术。本文采用基于双因子阈值函数和阈值选取的中值滤波算法，并把这种算法与提升小波分析相结合，进行空间外差光谱降噪处理。相对于传统的小波变换，基于提升小波变换的算法降噪效果更好，因此该算法具有一定的实用性。但提升小波分解层数需要不断地调整，且噪声估计不够精确，因此基于提升小波变换的算法在空间外差光谱消噪方面有更大的改进空间。