模逆矩阵的求法及其应用

翁世有

(苏州市职业大学 数理部，江苏 苏州 215104)

在通信过程中，特别是在军事、外交、商贸等领域，经常要对语音、数据、图像等信息进行加密和解密，以保障信息的安全。矩阵及线性方程组理论作为应用工具之一，在推广到模算术的密码系统，即由剩余系构成的有限域中时，涉及到矩阵同余和求模逆矩阵的问题。对于该问题，文献[1]研究了剩余类环上的二阶可逆矩阵问题，文献[2]给出了Zm上m阶可逆矩阵的计数问题。本研究将给出模逆矩阵的存在条件和求法，并给出在密码学中和求解多元未知数线性同余式组中的简单应用。

1 预备知识

1.1 模m同余

设A=(aij)m×n和B=(bij)m×n是整数矩阵，m是正整数，若

aij≡bij(modm)，1≤i≤m，1≤j≤n，

则称A和B关于模m同余，记作A≡B(modm)。

1.2 同余性质

命题1 设A和B都是m×n矩阵，满足A≡B(modm)，C=(cij)n×r和D=(dij)s×m都是整数矩阵，则有AC≡BC(modm)，DA≡DB(modm) 。

该性质可由数论同余的性质极易证明，略去。

2 模逆矩阵

2.1 定义

设A和B都是n×n 矩阵，满足AB≡BA≡E(modm)，其中E是单位矩阵，m是正整数，则称B为A的模m的逆矩阵。

2.2 模逆矩阵的性质

命题2 若B为A的模m的逆矩阵，且C≡B(mod m)，则C也是A的模m的逆矩阵。

事实上，因 C≡B(modm)，由命题1得，CA≡BA≡E(modm)，故C也是A的模m的逆矩阵；反之，若B与C都是A的模逆矩阵，由定义2，CA≡BA≡E(modm)，再由命题1可得CAC≡BAC(modm)，又AC≡E(modm)，所以C≡B(modm)。

3 模逆矩阵的求法

3.1 伴随矩阵法

3.2 初等变换法

由此，设P1，P2，…，Ps是初等矩阵，使得P1，P2，…，PsA=E，那么P1，P2，…，PsE=A-1。

在求模逆矩阵时，应注意倍法变换中所乘的数都是整数，逆矩阵中的元素取自模m的非负最小正剩余构成的集合。

4 模逆矩阵的应用

4.1 在密码解密中的应用

在模算术密码系统中[5]，经常由26个英文字母对应0-25个非负整数。 设多字母密码系统中，明文长度为n的数剧组为x1i，x2i，…，xni，密文中与它对应的是长度为n 的数据组y1i，y2i，…，yni，(i=1，2 ，…，n)，则有

这n个同余式可以用同余矩阵表示为

其中X和Y都是n阶方阵，其i行j列的元素分别是xij和yij，若，则得到加密矩阵为，满足，

那么A-1(mod26)就是秘钥。

4.2 在求解素数模的多元未知数线性同余式组中的应用

在数论中，求解多个模(两两互素)的线性同余式组的问题，可以用孙子定理。但是对于同一个模的同余式组，可以使用模逆矩阵或者线性方程组理论来解决。

例4求解下列三元同余式组

解：方法一(用模逆)

方法二(方程组理论)

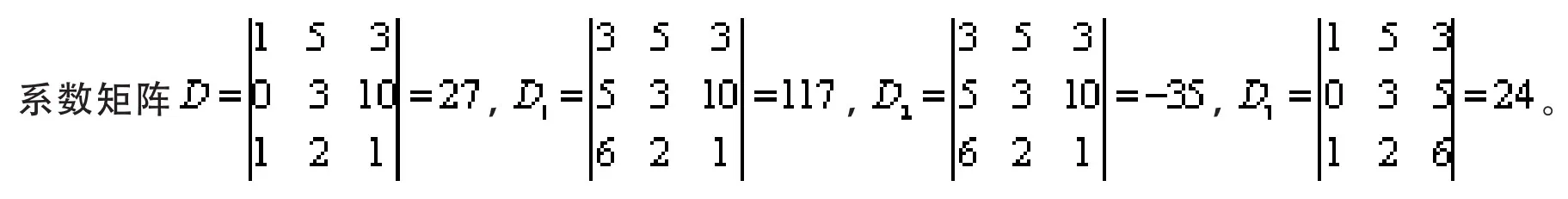
解三个一次同余式

Dx1≡D1(mod13)，Dx2≡D2(mod13)，Dx3≡D3(mod13)，得x1≡0(mod13)，x2≡4(mod13)，x3≡11(mod13)。

5 结论

本研究介绍了模逆矩阵的定义及基本性质，研究了模逆矩阵的存在条件，给出利用伴随矩阵和初等变换求模逆矩阵的两种求法，并通过例题展示了求模逆矩阵与传统的求逆矩阵的差异，给出了在模算术密码系统中模逆矩阵与加密钥的关系和求解多元未知数线性同余式组中模逆矩阵的应用。