基于卫星导航/惯性单元松耦合的低速智能电动汽车航向角估计
2020-06-16陆逸适高乐天余卓平
熊 璐,陆逸适,夏 新,高乐天,余卓平
(1.同济大学 汽车学院,上海 201804;2.同济大学 新能源汽车工程中心,上海 201804)
近年来,低速智能电动汽车发展迅速,组合定位技术是支撑其发展的关键技术,航向角估计是组合定位算法中的重要组成部分[1]。准确的航向角也是车辆轨迹跟踪控制的必要前提[2-3]。双天线GNSS(global navigation satellite system)接收机可直接输出车辆的航向角,然而,受制于成本,GNSS接收机输出的航向角通常采样频率较低,并且伴随有较大噪声和时间延迟[4],实时控制难以直接应用。智能汽车大多配备有高精度GNSS接收机、磁力计和惯性单元等传感器,现有研究大多利用这些多源传感器通过估计手段间接获取航向角。这些研究主要分为两类:GNSS/INS(inertial navigation system)组合方法,磁力计与IMU(inertial measurement unit)组合方法。
在GNSS/INS组合的方法中,航向角通常与俯仰角、侧倾角、速度和位置等状态一同在惯性导航系统INS中被解算,然后通过一个滤波器估计INS的误差,从而对惯性导航的误差进行修正[5]。当车辆正常行驶时,由GNSS/INS组合系统的误差状态方程可知,航向角误差在任意时刻并不完全可观[6-7],航向角误差只有在载体满足一定水平加速度激励的条件下才可以被准确估计,进而使用该误差对惯性导航中航向角进行修正。但对低速智能电动汽车而言,车辆本身无法提供较大的加速度激励,在常用的GNSS/INS组合架构下,航向角误差的可观性较差,从而导致航向角的精度难以保证。
也有学者通过利用磁力计对地磁进行测量,从而在进行姿态角解算时通过地磁对姿态角进行辅助估计。在无人机的应用中,方根在等学者对三轴磁力计进行了倾斜补偿,然后使用拓展卡尔曼滤波算法融合加速度计、陀螺仪和磁力计信息对无人机的姿态进行了估计[8]。Yoon等学者设计了一个随机滤波器,保证了在磁力计受干扰的条件下航向角估计器与磁力计的隔离[9]。然而,在电动汽车环境下,车辆磁场分布较为复杂,微弱的地磁很容易被车载电器周围磁场干扰,从而导致较大的角度测量偏差,进而导致航向角误差。
本文在低速智能电动汽车清扫车平台下,利用智能汽车搭载的GNSS和IMU传感器设计了航向角估计器,主要贡献在于创新性地基于残差自适应RAE(residual adaptive estimation)卡尔曼滤波器设计了GNSS/IMU松耦合(loosely coupled,LC)组合的航向角估计器:提出了基于IMU的航向角积分方法,推导了松耦合条件下误差动态与测量模型;针对GNSS信号质量时变问题,基于本文提出的航向角误差动态和测量模型,使用残差自适应卡尔曼滤波算法对航向角误差进行了估计。解决了IMU长时间积分累积误差问题,GNSS航向角测量频率低、噪声时变和存在异常值的问题。最后,通过在不同GNSS信号条件下进行的多组实车试验,验证了本文提出的航向角估计算法的有效性。
1 基于GNSS/IMU组合的航向角估计
受GNSS/INS组合方式启发,本文提出了GNSS/IMU LC组合的航向角估计方法。该方法架构如图1所示,主要包含3个模块:GNSS航向角接收模块,基于IMU的航向角积分模块,二者的误差通过一个RAE卡尔曼滤波算法进行滤波处理,滤波后的航向误差经过反馈作用于基于IMU的航向角积分模块。图1中,ψGNSS为GNSS接收机输出航向,ψI为IMU积分所得航向角,eψ为航向角估计误差,kψ为反馈系数。
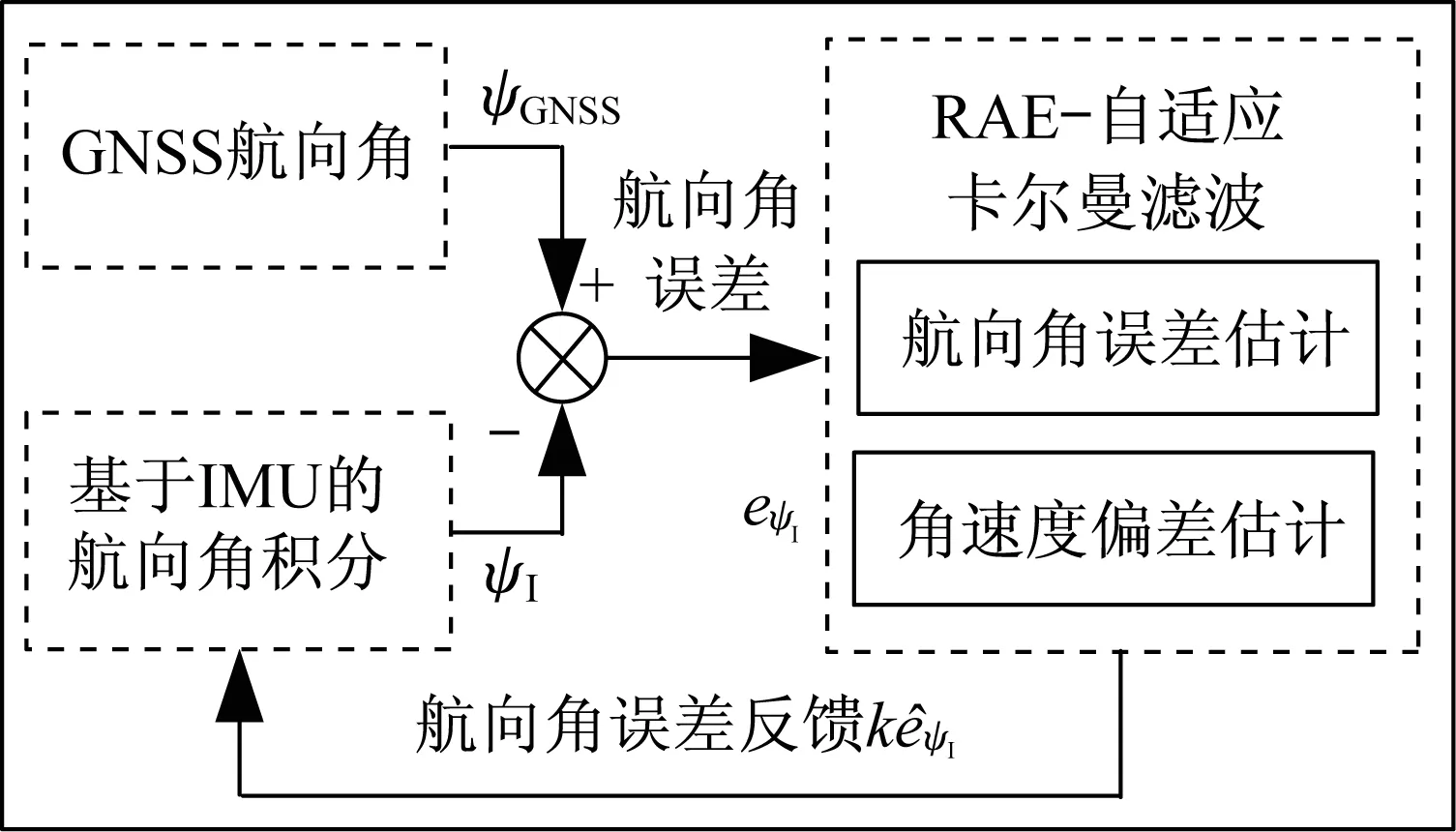
图1 航向角估计方法架构Fig.1 Structure of heading angle estimation method
1.1 基于IMU的航向积分方法
基于IMU的航向角积分方法由下式给出:
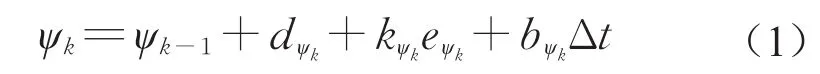
式中:下标k表示k时刻,k-1表示k-1时刻;ψk-1表示航向值;dψk表示k时刻横摆角速度增量,从IMU直接获取;eψk由航向角误差估计模块估计;bψk表示角速度零偏,由静止时IMU输出的角速度获取;Δt为IMU采样时间。
1.2 航向误差估计方法
1.2.1 航向误差估计测量模型
假设IMU积分得到的航向角和GNSS接收机输出的航向角满足如下关系:
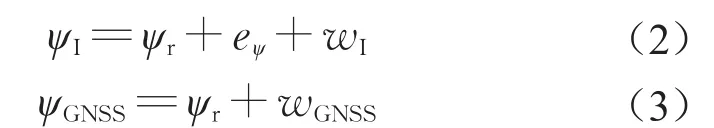
式中:ψr表示真实航向角;wI和wGNSS分别表示积分所得航向和GNSS接收机输出航向的高斯白噪声。
将式(2)和(3)作差可得航向角误差的测量方程
链路聚合技术是一种高效、高可靠性的技术,能够低成本的解决企业网络交换设备之间级联造成的带宽瓶颈,同时也提供了多线冗余的功能,现在已成为企业交换网络中主流的应用。

式中:η=wI-wGNSS表示高斯白噪声。
1.2.2 航向误差估计过程模型
航向角误差估计的动态由下式给出:

式中:上标点表示导数;w1和w2分别表示航向角误差动态和零偏的白噪声。进一步将连续方程改写为离散方程可得
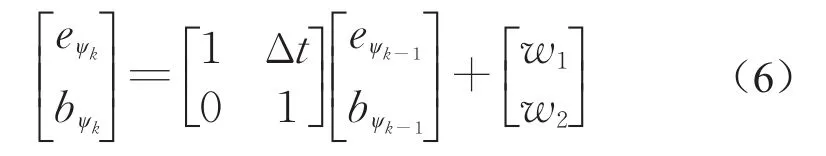
基于式(4)和式(6)所描述的系统,即可通过卡尔曼滤波算法对航向角误差进行估计。
1.3 本文自适应卡尔曼滤波算法
卡尔曼滤波算法结构如图2所示。图中,Gk表示卡尔曼滤波增益,Pk-1|k-1为k-1时刻协方差矩阵,Pk|k为k时刻协方差矩阵,Ck|k-1为测量矩阵,Ak-1表示k-1时刻系统矩阵,Pk|k-1为k-1时刻对k时刻预测的状态误差协方差矩阵,Rk为测量噪声协方差矩阵,I为单位阵,为k时刻最优状态,为k-1时刻最优状态,为k-1时刻预测k时刻的状态,zk为k时刻测量量,dt为时间步长,Γk-1为过程噪声的输入矩阵,Qk-1过程噪声协方差矩阵。
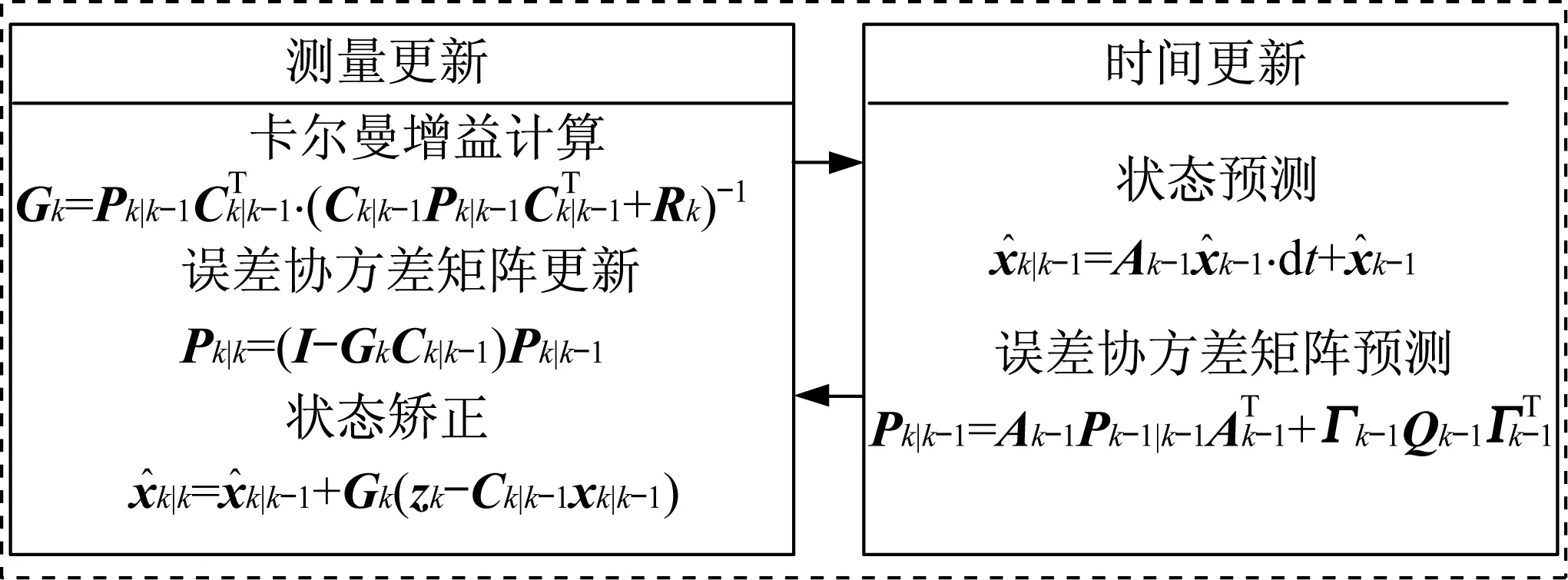
图2 卡尔曼滤波算法Fig.2 Kalman filter
因为GNSS信号易受干扰,在实际使用卡尔曼滤波时,测量噪声的协方差矩阵需要进行在线自适应估计,以保证滤波效果的稳健性。而系统噪声主要由IMU的噪声决定,一般变化较小,不再进行自适应。
k时刻航向角误差测量的新息dk和残差εk分别定义为
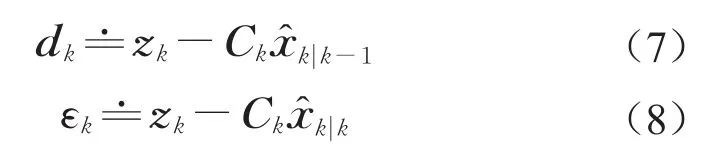
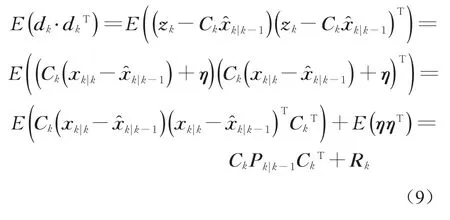
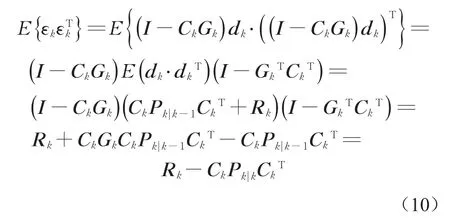

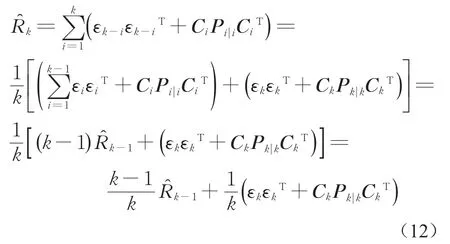
为了使算法对当前GNSS接收机输出的速度和位置统计特性具有更好的动态性能,使用渐消因子对过去时刻的测量值进行部分遗忘,削弱过去测量信息对当前估计的影响,渐消因子b为(0,1)之间的实数,根据渐消因子得到渐消系数αk为
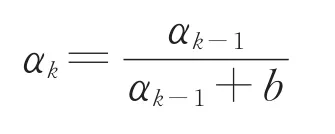

由于式(13)中包含(εkεkT+CkPk|kCkT),需要迭代运算,为了保证计算的合理性,避免引起滤波异常,因此需要对的各个元素的大小进行限制。这里需要对各个测量值依次进行约束,对于第i个量测有
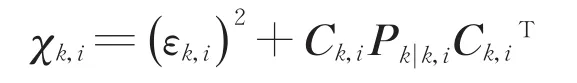
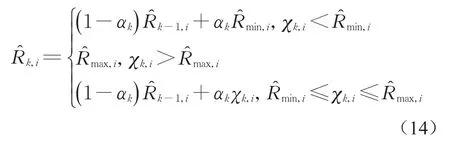
2 航向角误差反馈策略
前面已提到,GNSS信号易受外界环境干扰,如遮挡、多路径效应等,造成航向角测量中出现异常值,经过异常值进行量测更新后,即使测量噪声协方差矩阵已经进行了自适应处理,估计所得的航向角误差也不应再反馈至基于IMU的积分算法中,需要对这种异常情况设计策略对航向角误差反馈加以约束,如图3所示。当标志位Fψ=1时,反馈的航向角误差为0。

图3 航向角误差反馈策略Fig.3 Feedback strategy of heading angle error
图3中,下标GNSS表示对应GNSS接收机的变量,变量下标T表示相应变量的阈值,E()和Var()分别表示变量的期望和方差,下标E和V分别表示期望和方差,RRMS_Lati和RRMS_Longi分别表示GNSS接收机输出的纬度和经度的均方差误差,PPDOP表示几何精度因子。
3 试验结果与分析
为了对本文提出的算法进行验证,进行了离线和在线试验验证。离线试验是通过数据采集设备采集实车试验数据,然后使用Matlab/Simulink运算平台对算法验证。在线试验是通过嵌入式处理器在线接收IMU和GNSS信息,在处理器中对算法在线实时验证。
3.1 试验平台介绍
试验平台车为一台智能电动清扫车,如图4所示。该车作业最大车速为5 km·h-1。用于离线试验测试平台如图5所示。华测公司的P2组合导航产品测得的航向角用于作为参考值,Trimble BD982 GNSS接收机用于提供测量航向角,ADIS16490提供横摆角速度增量和横摆角速度信息,三者的串口信息通过STM32F103单片机转为CAN(controller area network)信号通过一台NI CompactRIO 9082数据采集设备采集,数据采集程序基于Labview 2013搭建,实车试验采集的数据在Matlab/Simulink中经过本文提出的算法处理对航向角进行估计。

图4 试验平台车:低速智能电动清扫车Fig.4 Test vehicle:Low speed autonomous electric sweeper
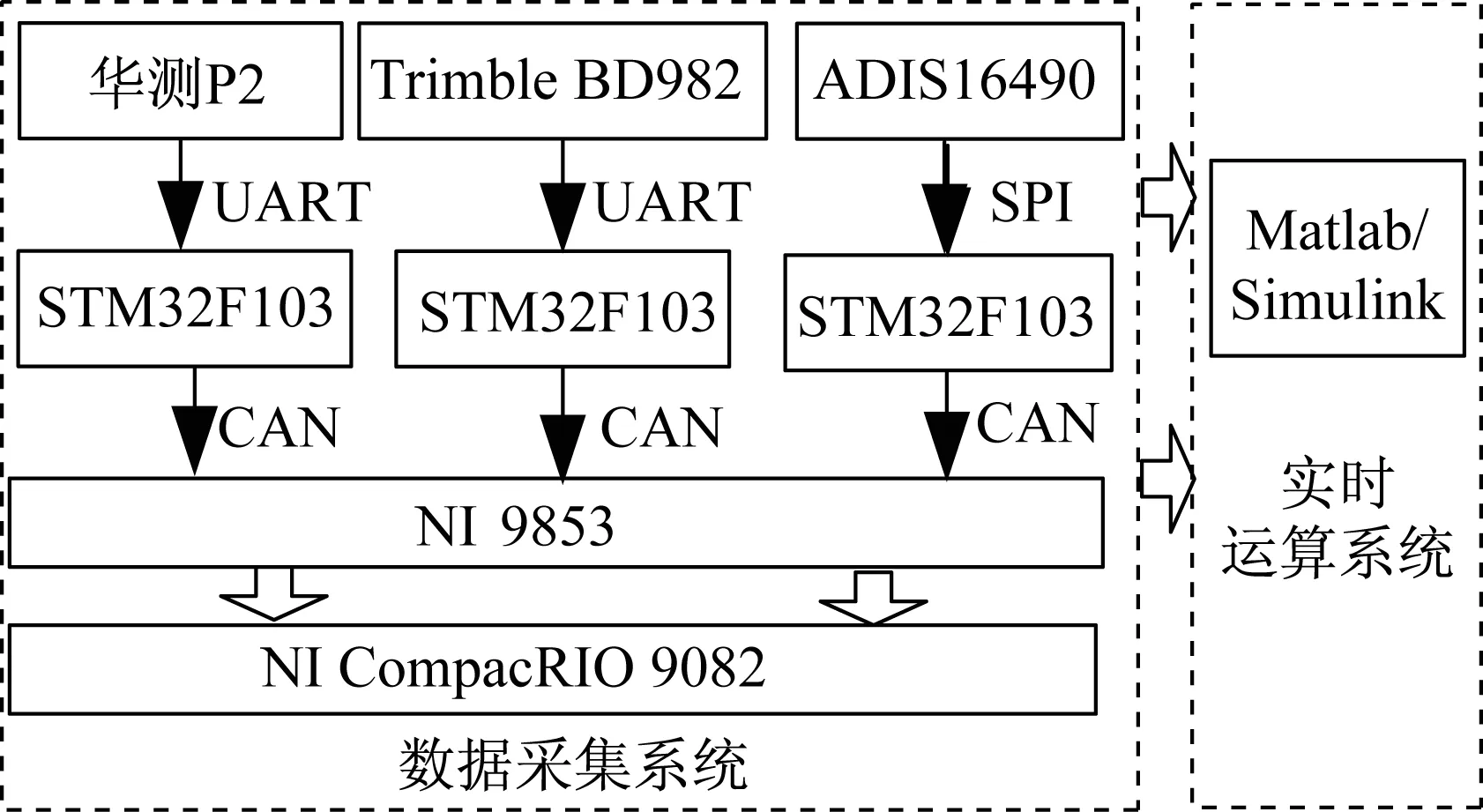
图5 离线测试试验平台Fig.5 Test platform for offline validation
实车在线试验验证平台如图6所示。与图5不同的是,这里使用了一块内核为DSP28335的工业级嵌入式控制器作为算法运算平台,控制器运行周期为10 ms。由于控制器在线数据采集变量个数受限于控制器资源,故只展示主要结果,更多算法细节在离线试验结果中展示。
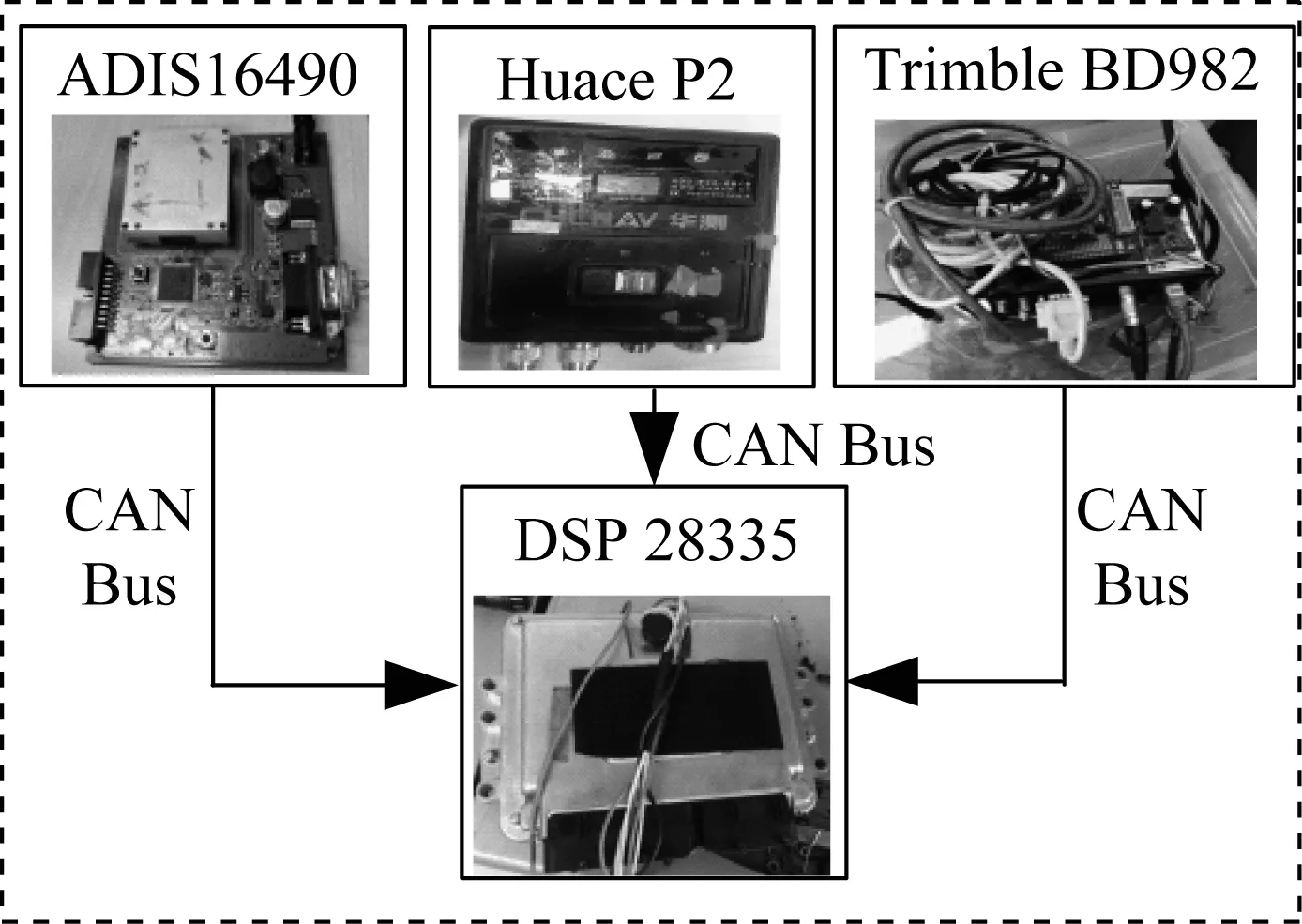
图6 在线试验验证平台Fig.6 Test platform for online validation
3.2 讨论与分析
图7和图8分别给出了离线和在线试验结果。由于离线仿真软件设置的计算精度与在线控制器相同,两种试验结果也基本相同,在离线试验中额外给出了测量协方差自适应结果。
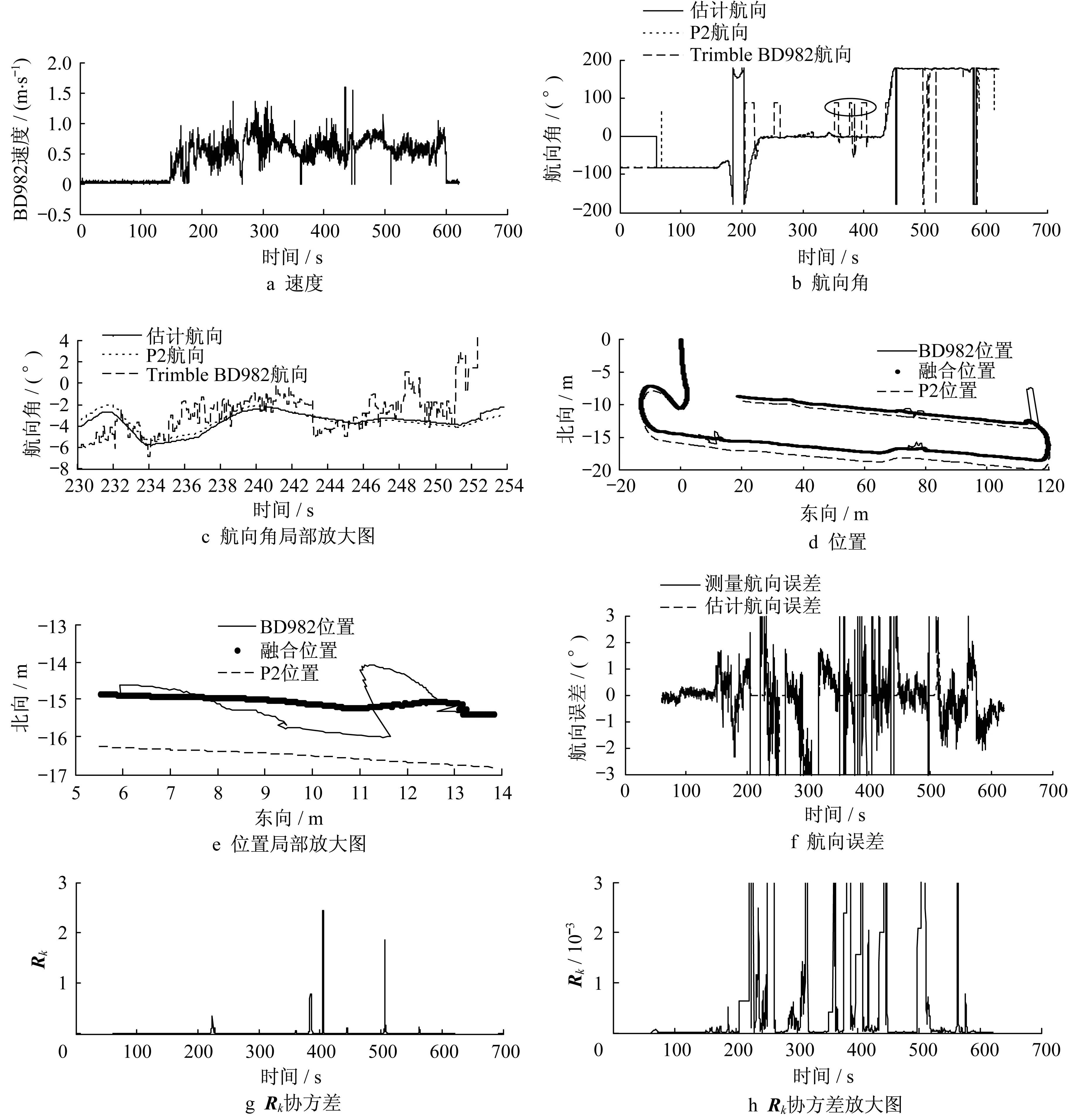
图7 离线试验结果Fig.7 Results of offline test
试验过程中,车辆行驶速度在1.5 m·s-1以下。Trimble BD982 GNSS接收机直接输出的航向角噪声较大,由图7b、图7c、图8b和图8c可以看到,航向角误差经过自适应卡尔曼滤波后噪声明显可以被削弱。由图7f可以看出,误差经过反馈至积分所得航向中对积分累积误差进行修正,由航向角局部放大图可以看到,修正后航向角相比于BD982更加平滑。图7b和图8b中圈出的GNSS测量航向异常值也可经过算法滤除。图7g和图7h中也可看到,自适应卡尔曼滤波中的协方差矩阵可随着测量噪声变化而改变,以减弱时变噪声对算法的影响。在实际应用中,将估计所得航向应用于车辆组合定位中,通过航向将车速分解至导航坐标系,进一步积分得到位置,如图7d和图8d。当GNSS接收机输出位置产生异常点时,如图7e和图8e,位置反馈被切断,位置由积分算法推算得到。可以看到使用估计所得航向进行推算得到的位置能够避免跳点,平滑度过GNSS信号异常区域,与华测P2推算所得位置较为接近。
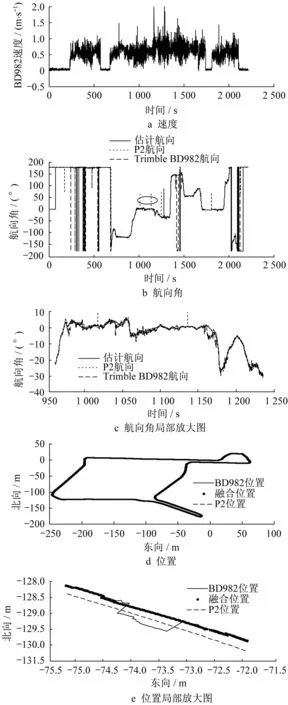
图8 在线试验结果Fig.8 Results of online test
总体上,由图7与图8以及表1和表2可以看出,航向角平均误差小于0.2°,航向角误差均方差小于0.6°,最大误差小于3°。误差较大的点出现在GNSS信号异常区域,由于华测P2中所使用的GNSS接收机为Novatel 718D板卡,而本研究中所使用的是BD982,二者差异可能也会导致两者航向产生误差,笔者团队后面将更换GNSS接收机对本文航向算法进一步验证。

表1 离线试验误差表格Tab.1 Estimation error of offline test (°)

表2 在线试验误差表格Tab.2 Estimation error of online test (°)
4 结论
基于低速智能电动汽车,本文研究了基于GNSS/IMU松耦合组合的航向角估计算法。得出以下结论:
(1)提出了GNSS/IMU松耦合条件下的航向角估计方法,设计了基于IMU的航向角积分方法,推导了松耦合条件下误差动态与测量模型,并基于此模型设计了航向角误差估计方法,从而对航向角间接估计。
(2)针对GNSS信号质量时变问题,使用残差自适应卡尔曼滤波算法对航向角误差进行了估计,为了减小计算量,基于渐消因子通过递推方式对测量噪声协方差矩阵进行了自适应。针对GNSS信号质量设计了航向角误差反馈修正策略。在不同GNSS信号条件下进行的多组实车试验验证了本文提出的航向角估计算法的有效性。
