离心叶轮叶片载荷分布优化设计*
2020-06-16任霁筇赵新君邵伟龙王国欣闻苏平
任霁筇 赵新君 邵伟龙 郭 伟 王国欣 闻苏平
(1.西安交通大学能动学院;2.沈阳鼓风机集团股份有限公司)
0 引言
随着各行业对离心风机需求的不断增大,离心风机在工业生产中的能耗占比也逐年攀升。因此,研发设计成本低、效率高且节能的风机非常重要。
早期离心式风机的设计和优化研究通常更依赖于设计者的经验和大量的试验验证,导致风机的设计普遍存在开发周期长、投入成本高等缺点。最近三十年,CFD技术的蓬勃发展极大地推动了离心式风机设计研究的发展,相对准确地计算风机内部流场的细节,并分析各部件的损失类型和损失占比,以及各种因素对风机气动性能的作用影响使CFD技术开始逐渐取代部分的试验研究,广泛应用在风机性能的验证和设计优化等方面。
目前,基于CFD技术对离心式叶轮进行设计研究的方法主要包括正问题和反问题设计方法两大类。对于正问题设计方法,研究者通常先选定一个初始几何结构,然后根据数值模拟结果不断修正,直到获得满意的结果。这种设计方法因操作相对简单而被广泛应用,在近些年的发展也相对成熟[1]。但这种设计方法需要大量的几何参数来精确地表示叶片的几何结构,目标函数形状通常相当复杂,需要大量计算并难以在设计中获得可用于类似设计问题的通用技术。相比之下,反问题设计方法则很好地补充了这些问题。反问题设计方法是通过给定叶片表面速度分布或者压力的分布等相关物理量,反向求解叶轮的几何形状结构。这种设计方法可以有效降低目标函数的复杂度,将设计任务简化进而减少总体优化时间。此外,由于反问题设计的设计参数与内部流场的关系更为密切,相较于正问题设计,可以得到优化后的叶片载荷分布,而非几何控制点的最优组合,这是一个更为普遍的结果,方便推广应用于类似的设计问题。
此外,单纯基于反问题设计思路并依靠CFD计算来设计流体机械部件仍存在一定盲目性,为进一步提高优化设计效率,工程上通常把数值计算方法和数值优化方法结合起来,以优化流体机械的结构及性能。
建立在“近似函数”理论上的优化方法作为一种快速兴起的优化算法,相对于梯度优化算法、直接搜索方法和全局优化算法等方法既克服了单一优化算法容易陷入局部最优解的缺点,又兼顾了数值算法的高效性。该方法通过利用数学模型逼近输入变量和输出变量,并采用近似模型来代替详细数值计算,以此减少所需的计算次数。同时,采用拟合模型的响应函数,提高收敛速度并确保全局优化。常用的拟合模型包括人工神经网络和响应面法这两类优化方法[2-5]。
W.Jansen[6]首次提出用流线曲率法计算扭曲叶片形状,通过给定叶片表面相对速度分布控制叶片表面载荷,计算得到叶片几何形状,再通过计算流场反复迭代进行修正。卢金玲等[7]建立了将反问题计算和神经网络、遗传算法结合起来的优化设计方法,间接地参数化叶片几何形状,并通过对混流泵的优化设计,证明了该方法的有效性。席光等[8]以叶片角为控制参数对混流泵叶片形状参数化,利用人工神经网络建立响应关系后再用遗传算法寻优,过程中针对设计变量多的问题,建立子系统对变量进行分类优化。Cho等[9]利用人工神经网格并基于非梯度的粒子群算法,对离心式压缩机的子午面与叶片型线进行优化,优化得到的叶轮效率和压比分别提高了1%、9.3%。Bonaiuti等[10]应用响应面法和多目标遗传算法分别对离心和轴流压缩机载荷分布进行优化,对于离心叶轮,轮盘侧载荷后加载、轮盖侧前加载以及叶片负倾斜,能够有效抑制叶轮内部二次流的发展,从而提高叶轮效率,研究还表明:叶片前缘载荷与喘振和堵塞裕度关系密切,载荷值为正时,不利于小流量工况条件下的叶轮运行,反之情况相反。
本文采用数值模拟的方法对某离心式风机叶轮的内部流场进行分析,基于反问题设计方法并结合响应面法与多目标遗传算法对叶轮叶片进行了优化设计,得到了比原始机翼型叶片叶轮具有更高效率的三元叶片离心叶轮,研究成果对同类型离心式叶轮叶片的优化设计也具有工程指导意义。
1 研究对象及反问题设计参数选取
选取了某离心风机叶轮为研究对象,该叶轮原始叶片为机翼型叶片。机翼型叶片结构相对复杂、制造成本高,且在运行过程中容易出现叶片磨损与积灰。而圆弧型单板叶片是由钢板轧制成型,强度高耐磨性更好,加工难度与制造成本相对较低。因此在不牺牲风机性能的前提下,应用优化方法设计出三元流单板叶片代替原有机翼型叶片。
1.1 几何模型
风机的工作介质为空气,设计工况下进口体积流量Qn=85 400m3/h,叶轮转速n=1 450r/min,进口压力Pin=101 325Pa,进口温度Tin=293K。叶轮基本结构参数如表1所示,三维实体模型与子午面几何分别如图1和图2所示。

表1 原始叶轮结构参数Tab.1 Structural parameters of original Impeller

图2 原始叶轮子午面几何Fig.2 Meridian geometry of original impeller
1.2 反问题设计参数选取
反问题设计的基本思想是叶片由一系列涡表示,涡的强度通过周向平均环量给定,由所给定的叶片周向平均速度环量分布,可以迭代计算得到叶片的几何形状[11]。
本文研究的离心叶轮叶片的优化设计首先根据一元流动理论计算出叶片前缘、尾缘环量,然后对叶片的载荷分布和积叠方式等相关变量进行优化,从而实现离心式叶轮的优化设计。
1.2.1 叶片前缘、尾缘环量计算
假定气体在叶轮进口处无预旋,叶片进口处环量(rVθ)1为0,而叶片出口环量(rVθ)2的初始值可以根据流动角与平均环量的关系确定。其中,叶片的流动角定义为该点相对速度和子午面之间的夹角,流动角β和叶片环量rVθ有如下关系:

出口流动角β2和出口子午速度V2m分别用以下关系式计算:


1.2.2 叶片载荷分布方式
叶片载荷分布方式的给定有不同的方法[12-13],本文通过分别给定近轮盘侧和轮盖侧从叶片前缘至尾缘的载荷分布(简称:轮盘侧、轮盖侧叶片载荷分布),从而实现叶片载荷分布的设置,叶片载荷分布的形式选择由两条线段的分布来表示,如图3所示。

图3 叶片载荷分布给定方法Fig.3 Given method for impeller load distribution
图3中横坐标是叶片的无量纲子午长度,纵坐标是环量rVθ沿无量纲子午长度的变化率(即载荷),叶片前缘及后缘附近的载荷分布均呈抛物线形。从图中可以看到,在轮盘侧和轮盖侧各需要4个设计变量来控制叶片载荷分布:
NC:第一段抛物线与直线的衔接处的无量纲子午长度;
ND:第二段抛物线与直线的衔接处的无量纲子午长度;
Slope:直线斜率,控制载荷分布的形式,正值表示后加载,负值表示前加载;
DRVT:前缘载荷,该值控制着叶片进口冲角。
研究采用设计工况下进口零冲角,因此轮盘、轮盖侧前缘载荷DRVT均为0。
综上所述,轮盘侧、轮盖侧叶片的载荷分布控制参数一共有6个。
1.2.3 叶片倾斜
叶片倾斜是叶片造型过程中的另一个重要参数,它会产生叶片展向的力,进而影响叶轮内部的流场载荷分布[14-15]。
叶片倾斜通过沿准正交线轮盘侧至轮盖侧的叶片包角变化来实现。积叠的准正交线可以选取在叶片前缘至尾缘的任意位置,对于离心式叶轮,通常设置在叶片尾缘。叶片积叠方式的定义如图4所示,图中θ是叶片尾缘某点的包角(柱坐标系中的角坐标)。从图4中可以看到,叶片尾缘轮盘侧到轮盖侧的叶片包角发生变化时,就能够改变叶片尾缘倾斜角,叶片尾缘倾斜如图5所示。当轮盘侧、轮盖侧叶片包角取相同的值,叶片尾缘的倾斜角度为0。

图4 积叠方式定义图Fig.4 Definition diagram of stacking mode
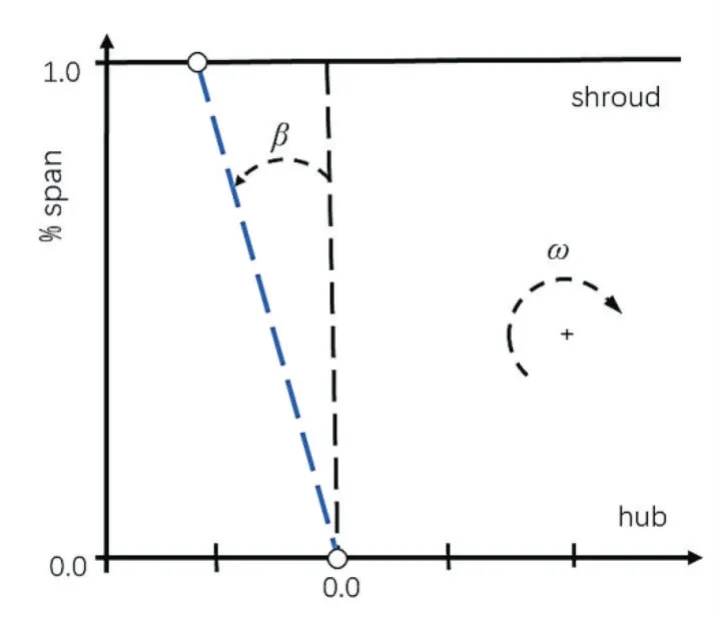
图5 叶片尾缘倾斜示意图Fig.5 Schematic diagram of blade trailing edge tilt
2 数值求解方法
使用Numeca软件完成研究对象的网格划分、流场计算及计算结果的后处理。
叶轮网格的划分由AutoGrid5模块自动生成HI拓扑结构,并对叶轮进出口分别进行了延伸。检验计算网格无关性过程中,对比了单流道叶轮在470 000,650 000,840 000,1 020 000和1 200 000网格数时的全压效率和全压,发现网格总数从840 000增加到1 200 000时,全压效率与全压的相对变化较小。因此,为减少计算量,本文采用840 000的单流道网格数进行计算分析。为了确保计算结果的准确性,网格正交性均>10°,长宽比均<2000,延展比均<5。网格划分如图6所示。

图6 原始叶轮网格划分示意图Fig.6 Schematic diagram of original impeller grids
数值计算使用FINE/Turbo模块进行。Spalart-Allmaras湍流模型作为连接代数Baldwin-Lomax模型和两方程k-ε模型之间的“桥梁”,由于其鲁棒性好,处理复杂流动能力强,近年来受到了许多数值计算工作者的欢迎。与Baldwin-Lomax模型相比,S-A模型的主要优势是湍流涡粘性场总是连续的;相比于k-ε模型,SA模型的主要优势是其鲁棒性和较低的CPU时间及内存使用率。因此选取Spalart-Allmaras一方程湍流模型对时均湍流三维雷诺平均N-S方程进行定常求解,并采用多重网格、隐式残差光顺以及当地时间步长等加速收敛技术提高收敛速度。
工作介质设置为空气,进口边界条件设置为总压Pin=101 325Pa,总温Tin=293K,轴向进气,出口边界条件设置为质量流量,固定壁面、绝热、无滑移,当全局残差达到10-6时认为计算收敛。
3 基于响应面法与多目标遗传算法的叶片载荷分布优化
基于响应面法与多目标遗传算法对离心叶轮进行优化。保持子午流道不变,通过控制叶片载荷分布及叶片倾斜,生成优化方案。
3.1 响应面法
响应面方法RSM(Response Surface Method,RSM)是将试验设计和数理统计相互结合起来的数值优化方法,由于它的易操作性被广泛应用于数值最优设计。应用RSM主要包含选择响应面的近似函数模型和用于评估响应函数的一组试验点,并基于试验的结果构造响应面的逼近函数,评估函数的逼近性能后,再应用于优化设计研究。
RSM用多项式近似目标函数,且通常使用一阶或二阶多项式函数:

式中,X为设计参数;β为回归系数,该值表示了自变量对因变量作用的大小;Y是样本点响应值。求解多项式拟合的关键就是求出回归系数β,通过标准最小二乘法确定,它使一组点的预测值与实际值偏差的平方和最小化。
为了评估响应面函数对试验点的拟合程度,即响应面模型的预测能力,引入相关系数R2进行评估。用于拟合多项式的回归分析,其定义如下:
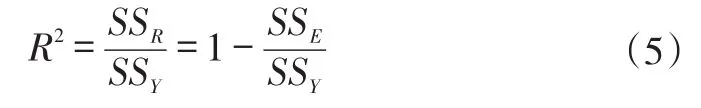
其中,SSY是响应值和相应均值差的回归平方和;SSR是响应值和相应估计值差的平方和;SSE是相应估计值和相应均值差的平方和。
3.2 多目标优化算法
在流体机械的优化设计过程中,需要对不同目标同时进行优化,属于多目标优化MOP(Multi-objective Optimization Problem,MOP)的范畴。MOP的数学表达式为:
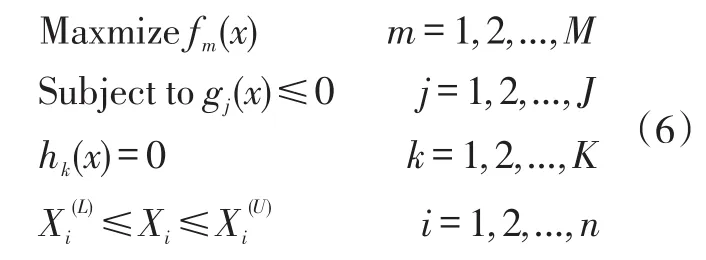
式中,fm(x)是第m个子目标函数,M是子目标函数的数量;g(ix)是第j个不等式约束条件,J是不等式约束条件的数量;h(kx)是第k个等式约束条件,K是等式约束条件的数量;Xi是第i个设计变量,n是设计变量的数量,则分别是第i个设计变量取值的上限与下限。
第二代非劣排序遗传算法NSGA-Ⅱ[13](Nondominated Sorting Genetic Algorithm-Ⅱ,NSGA-Ⅱ)是多目标优化算法中的一种优秀算法。
在NSGA-Ⅱ算法中,作为交叉操作与变异操作的运算机制使用是一种称为SBX(Simulated Binary Crossover)的方法。其中,交叉算子为:
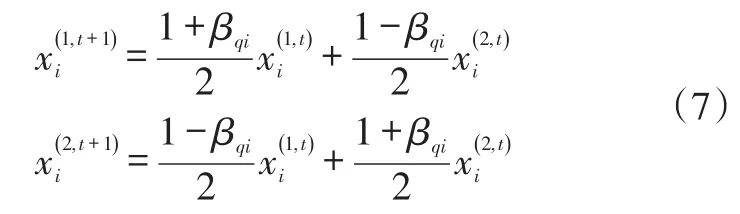
变异算子为:
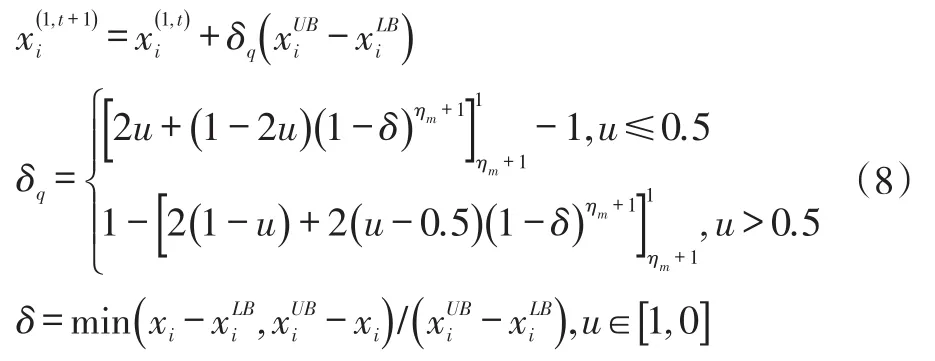
3.3 叶片优化设计流程
叶片优化过程中设计变量共有7个:控制轮盘侧叶片载荷分布的NCH,NDH,SlopeH,控制轮盖侧叶片载荷分布的NCS,NDS,SlopeH,以及控制叶片倾斜的Stacking。给定初始设计变量的取值及范围,如表2所示。

表2 设计变量初始取值及范围Tab.2 Initial value and range of design variables
为保证风机在全工况下运行时都具备较高的效率,选取风机在设计点、相对流量80%和120%流量点的全压效率作为优化目标,另外考虑到叶片强度等机械方面要求,同时选择任意位置准正交线上,轮盘、轮盖侧叶片包角最大差值MaxLean(叶片倾斜)作为补充优化设计目标。风机全压效率定义如下:

采用响应面方法建立函数的近似模型,通过最小二乘回归,得到与设计变量相关的气动性能近似响应函数,并对模型的有效性进行验证。
建立近似模型后,将多目标遗传算法应用于所获得的响应函数,首先优化得到最优解的Pareto前沿,然后在Pareto前沿选择不同设计变量组合的最佳方案,整体优化设计流程如图7所示。

图7 优化设计流程图Fig.7 Flow chart of optimization design
3.4 优化结果
在获得的Pareto前沿中,选择其中一个较优配置作为优化叶轮,对应的设计变量取值如表3所示。

表3 优化叶轮设计变量取值Tab.3 Design variable values for optimized impeller
优化叶轮的叶片载荷分布及叶轮三维实体模型图分别如图8和图9所示。

图8 优化叶轮叶片载荷分布Fig.8 Blade load distribution for optimized impeller

图9 优化叶轮三维模型图Fig.9 3D model for optimized impeller
4 结果与分析
4.1 总体结果分析
经数值计算,优化前后叶轮主要气动性能对比如图10和图11所示。经过载荷优化后,优化叶轮在设计工况下达到了原始叶轮全压,全压效率为96.71%,相对于原始叶轮全压效率提高1.3%,在全工况范围内,全压效率均有明显提高。

图10 优化前后叶轮全压效率对比Fig.10 Total pressure efficiency comparison of original and optimized impellers

图11 优化前后叶轮全压对比Fig.11 Total pressure comparison of original and optimized impellers
4.2 流场分析
图12~图17依次为设计流量工况、80%流量工况优化前后叶轮出口截面和90%叶高位置相对速度分布图以及120%流量工况优化前后叶轮出口截面和95%叶高位置相对速度分布图。
通过分析可知:原始叶轮出口位置,叶片非工作面靠近轮盖一侧在不同流量下均存在较大的流动分离,且流动分离随流量的减小而逐渐增大。优化叶轮下,各流量工况在该位置的流动分离现象均得到了明显改善。
通过对图14分析可知:优化设计显著改善叶轮出口非工作面盖侧流动的同时,也使得盘侧的流动分离增大。
通过对图18进行补充分析可知:在120%流量工况95%叶高位置,原始叶轮在叶片压力面中段存在小面积的低速区,而在叶片吸力面出口附近出现大面积的边界层分离。优化叶轮相较于原始叶轮在显著改善非工作面流动的同时则在一定程度上使工作面的流动分离加剧。

图12 叶轮出口截面相对速度分布图(设计流量)Fig.12 Relative velocity distribution of impeller at outlet(design flow rate)

图13 90%叶高相对速度分布图(设计流量)Fig.13 Relative velocity distribution at 90%blade height(design flow rate)

图14 叶轮出口截面相对速度分布图(80%流量)Fig.14 Relative velocity distribution of impeller at outlet(80%flow rate)

图15 90%叶高相对速度分布图(80%流量)Fig.15 Relative velocity distribution at 90%blade height(80%flow rate)

图16 叶轮出口截面相对速度分布图(120%流量)Fig.16 Relative velocity distribution of impeller at outlet(120%flow rate)

图17 95%叶高相对速度分布图(120%流量)Fig.17 Relative velocity distribution at 95%blade height(120%flow rate)
5 结论
本文基于离心风机反问题设计思路,选取叶轮的轮盘、轮盖侧叶片载荷分布及叶片尾缘倾斜作为优化设计变量,并采用响应面法与多目标遗传算法相结合的优化策略,对设计变量进行优化,使叶片靠近轮盖侧非工作面在不同流量下的流动分离均得到了有效抑制,得到了比原机翼型叶轮更高效的三元单板型离心式叶轮。对比优化前后离心叶轮的性能和流场表明:
1)经过载荷优化后,优化叶轮在设计工况下达到了原始叶轮全压,全压效率为96.71%,相较于原始叶轮全压效率高1.3%,在全工况范围内,全压效率也均有明显提高。
2)原始叶轮出口位置,叶片非工作面靠近轮盖一侧在不同流量下均存在较大的流动分离,且流动分离随流量的减小而逐渐增大。优化叶轮下,各流量工况在该位置的流动分离现象均得到了明显改善。
