全景式数学教育对“迁移”的全景解读

张宏伟

[摘要]对“迁移”这个概念追根溯源、旁征博引，综合、创新性地提出应该从9个维度去理解、厘清“迁移”这个概念——数学中的迁移，并不仅仅是学习者将“先验因素”移动到新情境中（或另一种情境），更重要的是“移植”。同时，提出了“自体迁移、异体迁移、逆向正迁移、顺向正迁移”等概念，并总结出了“‘全景式数学教育使用‘迁移功能进行有效教学的基本流程”，分享了“负迁移的破解——‘垂线教学案例片段”“跨学科、跨领域的顺向正迁移案例”“逆向正迁移案例”三个非常经典的全景式数学教育“迁移”教学实录。

[关键词]迁移;全景式数学教育;全景解读;移植;全景式数学案例

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）17-0014-04

全景式数学教育团队精选了小学数学教学中常用的几十个核心概念，对其构成逻辑、具体内涵及其发展，以及如何更有效地用其教学等方面进行了全面、深入、立体的解读，并选摘了其中20个汇编成《小学数学20个核心概念的全景解读》一书。下面，就分5个模块展开对“迁移”这个概念的全景式解读。

一、概念构成逻辑的分析与追溯

综上，我们认为数学中“迁移”中的“移”是移植，即指将已有的知识经验、思想方法、身体五觉、情感态度等不仅转移至新的问题情境中，而且在新的情境中生根、发芽、繁殖、复活、应用。

3.“迁移”概念的整体解读

（1）“迁移”在汉典中的解释

①离开原来的所在地而另换地点。

②由于自然力的作用从一地移向另一地。

（2）“迁移”在辞海中的解释

①搬移;从一处搬到另一处。

②变迁，变化。

③指时间的流逝。

二、课程标准、心理学与教育学专著等对“迁移”的界定和论述

《当代教育心理学》指出，迁移是指“在一种情境中的技能、知识和理解的获得或态度的形成对另一种情境中的技能、知识和理解的获得或态度的形成的影响”。

《小学数学教学中的“迁移”》指出，迁移教学的实质就是让学生运用旧知识探索新知识，发现新规律，不断重组自己的认知结构。而马春圣在《迁移规律及其在小学数学教学中的运用》中强调，迁移的实质就是学习者运用原有认知结构的观念对新课题进行对比、分析、概括的过程，即原有认知结构与新课题的“同化、顺应的过程”。

《什么是学习的迁移》指出，学生在学习过程中，总是按照自己已有的知识经验来掌握新知识、新技能的。这些已有的知识经验会对学习新知识、新技能发生一定的影响，这种现象，在心理学上叫作学习的迁移（包括知识的迁移和技能的迁移）。已有的知识经验对新知识、新技能的学习起积极的促进作用，这是正迁移;相反，起消极的妨碍作用，就是负迁移。

《义务教育数学课程标准（2011年版）》没有给出迁移的详细阐述，但培养和发展学生的迁移能力是小学数学教学承载的任务之一。

三、全景式数学教育团队对数学学习概念“迁移”的理解

结合上述的追溯，参照心理学、教育学、课程标准和名家的研究，加之我30多年的教学实践与感悟，窃认为数学中的“迁移”应该从以下9个维度去理解、厘清和应用。

1.数学中的迁移，不仅仅指知识、技能、思想、经验和方法等智力因素的迁移，还包括身体五觉、情感态度等非智力因素。这一点和类推截然不同，类推更偏向理性，而迁移则感性与理性并重，比如爱屋及乌不是类推，而是情感的迁移。（注：文中把学习者以前在学习中获得这些可迁移的因素统称为“先验因素”。）

2.数学中的迁移，并不仅仅是学习者将过往学习中的上述“先验因素”移动到新情境（或另一种情境）中，更重要的是“移植”，即这些“先验因素”在新情境（或另一种情境）中能生根、发芽、生长、繁殖，并发挥作用，使得新问题因为这些“先验因素”的应用而得到有效解决或形成新障碍，即前面的学习对后续学习的影响。我们认为这种影响几乎无所不在，一切新的有意义的学习都是在原有的学习基础上产生的，不受学习者原有认知结构影响的学习是不存在的。

3.迁移的发生起于当下问题情境的诱发。学习者通过对当下问题的觉察（包括判断、分析、表征等等），唤醒身心中与之相关、类似的“先驗因素”，产生共情、类比（类化）、移植、类推的冲动，并付诸行动。

4.就迁移前后的情境对比而言，数学中的迁移最起码应包含两个基本类型：一是学习者在简单环境中习得的“先验因素”迁移到复杂的环境中，它仍然能复活、开花、结果，实现新成长。二是在认知的低阶段习得的上述因素迁移到高阶段。

5.就迁移前后的领域对比而言，迁移可以是同领域的进阶性或退阶性迁移，也可以是从一个领域到另一个领域的迁移。

6.从迁移的对象来说，包括自体迁移和异体迁移。自体迁移是学习者自己学习的“先验因素”对当下或后续学习的影响。异体迁移是他人的“先验因素”被自己觉察到，继而对自己当下或后续的影响。在课堂学习中，包括同学的“先验因素”对自己当下和后续学习的影响，以及教师的“先验因素”的影响。

7.从迁移对新（另一种）情境所起的作用来看，分为正迁移和负迁移。我们又把正迁移细分为逆向正迁移和顺向正迁移。关于正迁移，我们通常注意到的是顺向正迁移，而往往会忽视或者不能够充分地利用逆向正迁移。

8.关于顺向正迁移，大部分教师都是研究数学内部的迁移，而全景式数学教育不仅考虑到数学内部的迁移，还考虑到跨学科的迁移。

9.教师备课时，要充分调查、了解、分析每个学生的“先验因素”，并做出教学应对：比如，对于缺失“先验因素”的可能要设计相应的生活实践活动进行补充，对于可能产生负迁移的思考如何引导学生突破，对于不充分的如何进行丰盈，等等。

四、“全景式数学教育”使用“迁移”功能进行有效教学的基本流程

第1步入境——教师或者学生共同营造新的问题情境。

第2步觉察——学生通过对当下问题情境进行感觉、判断、分析、理解和表征。

第3步唤醒——学生唤醒身心中与新的问题情境相关、类似的“先验因素”，产生共情、类比（类化）、移植、类推和尝试解决新问题的冲动。

第4步移植——学生尝试把一些“先验因素”单独或者综合与新情境进行匹配，同时尝试用这些“先验因素”并结合当下的新的解决条件对新问题进行同化。如果解决成功，则为正迁移，并强化迁移意识;如果造成障碍，则为负迁移，负迁移发生后，学生尝试置换、调整、重新组合“先验因素”，再次尝试，如此反复，抑或另辟全新的蹊径，抑或顺应。

第5步应用和巩固。

第6步升华——学生回顾问题解决历程，并对自己的心路进行再次觉察，强化经验或形成新的“先验”，为后续的学习奠定更高阶或者新的迁移基础。

五、全景式数学教育中的“迁移”教学典型案例

任何知识的学习都会受前学习经验的影响，有的是正向的、有的是负向的，教师要避免负迁移带来的影响，充分发挥正迁移的助长功能，从而促进学生更好地学习。

[案例1]负迁移的破解一“垂线”教学片段

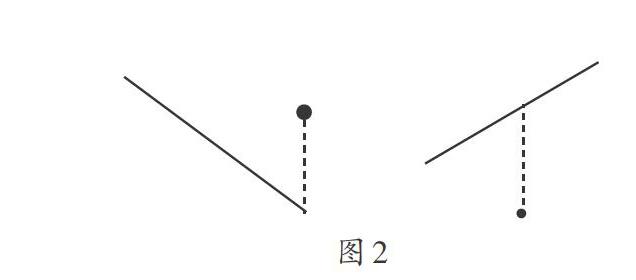
过直线外一点作已知直线的垂线段时，大致可分为如下三种情况：

对于图1-1，所有学生都能顺利完成，而对于图1-2、图1-3，很多学生会出现如下错误：

出现这种错误的原因是学生生活中的垂直和垂线经验的负迁移。生活中常见的房屋、门窗上的垂直、使用铅锤确定是否垂直的现象，以及测量各种物体高度（一般是垂直于地面）等的生活经历对学生造成的影响，使得学生缺少“斜的垂直”的实际生活体验，形成“垂直、垂线”是直上直下的思维定式，迁移到数学上，就会对图1-2、图1-3两个图形的作图理解出现障碍。

为了突破负迁移带来的影响，帮助学生积累与图1-2、图卜3作图相应的实际生活体验，建立正向的迁移，我们把学生带到操场上玩起了立定跳远游戏。

像这样画了三条不同方向的起跳线后，学生站在起跳线上并不都是面向一个方向的，而是对着自己的正前方，其实这也就是找到了已知直线的垂直方向。学生跳完之后，组员用皮尺测量每个人跳远的长度，测量的过程就是找到了直线外一点到已知直线的垂线段，其长度就是点到已知直线的距离。活动结束后，学生回到课堂上画垂线段时，图1-2、图卜3的作图问题便迎刃而解。这个课例提醒我们，很多负迁移的影响是学生储备的经验单一、不完整造成的，我们在教学中一定要注重对学生的“先验因素”进行补充、矫正和丰富，以期破除负迁移、建立或强化正迁移，实现高效的教与学。

[案例2]跨学科、跨领域的顺向正迁移案例

学习百分数这个主题单元时，大多数学生对于将问题“甲比乙多百分之几”转化成“乙比甲少百分之几”理解非常困难。比如：男生人数比女生多1/2，那么女生人数比男生少几分之几？由于受低年级学习过的“甲比乙多2个，就是乙比甲少2个”数的大小比较的经验影响（负迁移），一开始，大多数学生都会误认为“男生人数比女生多1/2，就是女生人数比男生少1/2”。为了解决这个问题，我们就与语文教师协作，给学生补上了语文领域的顺向正迁移的“先验因素”——语文的语法——“承前省”。

1.语文教师教学“承前省”

例1：船里装载的是新米，把船身压得很低。（叶圣陶《多收了三五斗》）

师：什么把船压得很低？

生：新米把船压得很低。

师：“新米”一词没写出来，你是怎么知道的？

生：我是联系前一句话知道的。

师：这个例子中省略“新米”一词会使语言更加简练，这在语文上叫省略主语，也就是承接前文省略主语，简称“承前省”。

例2：四大娘的脸色立刻变了，一句话也没说，提了水桶就回家去。（茅盾《春蚕》）

师：谁一句话也没说就回家了？谁提了水桶就回家了？

生：四大娘。

师：句中后面几个分句的主语因为承接前一分句的定语“四大娘”而省略。

例3：家破人亡之感立时袭进他的心，禁不住渗出两滴眼泪来，望出去，电灯人形都有点模糊了。（叶圣陶《潘先生在难中》）

师：这个例子中后面几个分句的主语承接前一分句宾语的定语“他”而省略。

2.数学教师教学过程

（1）师生一起在语文学习的基础上弄清楚数学中的“承前省”

数学其实也是有“承前省”的。比如“男生比女生多的人数占女生人数的几分之几”省略为“男生比女生多几分之几”，“女生比男生少的人数占男生人数的几分之几”省略为“女生比男生少几分之几”。

（2）“承前省”还原式解决问题

①男生有6人，女生有4人，男生比女生多几分之几？

第一步，将“男生比女生多几分之几”还原为“男生比女生多的人数占女生人数的几分之几”。

第二步，男生比女生多的人数是2人，女生是4人，男生比女生多的人数占女生人数的几分之几就是求2人占4人的几分之几。

第三步，列式（6-4）÷4=1/2。

②男生有6人，女生有4人，女生比男生少几分之几？

将“女生比男生少几分之几”还原为“女生比男生少的人数占男生人数的几分之几”，即2人占6人的几分之几→1/3。

（3）比较感悟

在①②中，学生悟出：虽然男女生人数都是相差2人，但①是拿2人和女生人数比，②是拿2人和男生人数比。引導学生将其和低年级学过的“男生有6人，女生有4人，男生比女生多几人？男生有6人，女生有4人，女生比男生少几人？”进行比较，学生就会发现：男生比女生多2人就是女生比男生少2人，具体的数量是可以颠倒叙说的。但是，这2人和男生比占1/3，这2人和女生比占1/2，是不能颠倒的。至此，学生进一步理解和掌握“甲比乙多（少）几分之几”的本质含义。

（4）跟进练习

练习1：松树有8棵，柳树有10棵。

①松树比柳树少（）棵。

②柳树比松树多（）棵。

③松树比柳树少几分之几？还原为（），就是求（）棵是（）棵的几分之几，列式__。

④柳树比松树多几分之几？还原为（），就是求（）棵是（）棵的几分之几，列式__。

⑤先把①②和③④比較，让学生发现“量”可以反着说，“率”不能反着说。

练习2：奶糖比水果糖多2/3千克，能不能说水果糖比奶糖少2/3千克？（能）奶糖比水果糖多2/3，能不能说水果糖比奶糖少2/3 7（不能）

教学中发现，通过将知识跨学科顺向正迁移，能帮助学生突破学习困难，促进学生更好地理解新知。

[案例3]逆向正迁移案例

逆向正迁移是指后面的学习影响前面的学习。如发展心理学和教育心理学的学习对先前普通心理学的理解产生影响，这就是逆向正迁移。逆向正迁移可以使原有的经验、知识结构得到充实、修正、重组或者重构等。顺向正迁移和逆向正迁移既有区别，又相互联系。我们往往更多地重视和应用顺向正迁移，而忽视逆向正迁移，显然这是不够全面的。事实上，逆向正迁移在学习中也起着很重要的作用。后面学习到的知识、思想、方法、情感、态度等，倒过来也可以迁移到以前学过的内容和情境中，这种逆向正迁移，会让学生打通知识间的连接，对以前学过的相应内容产生豁然开朗的之感，学生也能理解得更深入、更透彻，跃至更高阶的数学思维阶段。

如57+98=57+100-2，对于二、三年级学生的教学是基于生活的实际情景，通过现场实操帮助学生理解两种不同的简便算法：

小明收集家里废品到小区收购站售卖，一月份收入57元（5张10元+7张1元），二月份收入98元（9张10元+8张1元），怎么能很快算出小明两个月一共收入了多少元？

第一种想法：从57元中拿2元（一2）放入98元中凑成100，即57+98=57 2+100。

第二种想法：假设小明2月份兜里装着1月份的57元去卖废品应得98元，结果收购员没有零钱，直接给了小明100（+100），小明应该返还收购员2元（-2）即57+98=57+100-2。

此时，学生能看出两种简便算法都有+100、都有一2，但几乎所有的学生都认为这两种算法绝对不是一回事。到了高年级，学生学习了等式的性质、等量代换、运算律以及负数的认识后，就会意识到57+98=57 2+100和57+98=57+100-2本质上是一回事。

又如，学生在四年级学习乘法分配律后，再回过头来看二年级学过的两位数乘一位数的口算（23x4→先算20x4=80→再算3x4=12→最后用80+12=92），就能发现其原来就是在使用乘法分配律：23x4=（20+3）x4=20x4+3x4=80+12=92。其理、其情逆向迁移到二年级学习过的内容，学生对两位数乘一位数的口算和乘法分配律的算理都有了更为深刻的理解，而且对口算和分配律的学习情感也得到丰盈和升华，更重要的是，让学生打通和发现了二年级和四年级知识的联系，让学生有一种通透、惊喜和豁然开朗之感。

最后，需要强调和说明的是，顺向迁移与逆向迁移是高度相关、密切联系、相互影响、相互转化的。

（责编金铃）