基于粒子群算法的桥梁多目标维护决策优化

程 健，黎恩华

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引 言

桥梁是长期暴露在环境中承受荷载作用的构件,其性能会随着时间的增加而降低,导致其完成设计预定功能时失效概率增加。本文采用可靠度指标对桥梁性能进行评估,通过可靠度指标大小与桥梁容许可靠指标进行对比,来决定是否对桥梁进行维护。对同一桥梁,采用不同维护方式必然带来不同的性能提升和维护费用,因此对结构而言,需要对维护方式决策进行优化。

粒子群算法具有算法规则简单,需要调整参数少,计算收敛速度快,在工程应用中得到广泛使用。彭建新[1]等将粒子群算法用于桥面铺装的维护决策中;徐龙[2]等采用粒子群对路面维护资金进行优化分配,使预算能进行合理利用。

本文将简支梁看做由T梁组成的串联系统,将该桥中各梁的维护成本和维护效应分别用m行n列矩阵R和C表示,行数代表T梁的根数,列数代表一根T梁的维护策略数,采用多目标粒子群算法,以全桥可靠度大于容许值作为约束条件,以维护后桥梁可靠度最高和所需维护成本最低为目标函数对各T梁维护策略进行筛选,最终得到该桥最有维护策略的pareto最优解集。

1 JC法可靠度分析方法

1.1 结构可靠度理论

结构可靠性由安全性、适应性、耐用性组成;结构可靠度表征结构完成其设计时预定功能的概率。能完成该功能的概率被称为可靠概率,用Ps来表示;反之称为失效概率,用Pf来表示。通过这两个指标。可对结构实际情况有更具体的表征。

1.2 JC法

结构的可靠性分析中,通常将可能影响结构性能的重要参数视为随机变量X=(X1,X2,…,Xn)T,其中Xi表示第i个随机变量,相应的结构的极限状态函数表示为:Z=g(X)=g(X1,X2,…,Xn)。采用JC法计算可靠度,首先要对结构极限状态函数进行泰勒展开并保留一阶偏导项,设展开点为x*:

(1)

根据式(1),可以近似地得出极限状态函数Z的均值和方差:

(2)

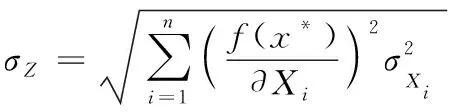
(3)

根据式(2)和式(3)即可求得可靠度指标值β:

(4)

2 粒子群算法

粒子群算法是将鸟类寻找食物的思维方式用来对实际问题进行优化的,一群鸟在空间内寻找同一时间几乎只有一块的食物,没有鸟知道食物的具体位置,每只鸟只知道食物距离自己的大概距离,并将该距离在鸟群中共享,根据每只鸟所记录的其自身最优位置(个体极值)和同一确定时刻鸟群中所有鸟中位置最优的鸟所在位置(群体极值)来对鸟群速度和位置进行更新。粒子群算法的主要参数有m(种群规模),w(惯性权重,表示继承先前粒子的能力),C1、C2(学习参数,前者为自身学习,后者为粒子间互相学习),最大迭代次数(Gmax运行结束判定条件)。

3 实例

3.1 桥梁横断面

30 m跨径预应力简支T梁桥,桥梁安全等级为二级,由6片预应力简支T梁组成,桥面宽度为13.75 m,保护层厚度为50 mm,平均温度20℃,平均湿度80%。主梁混凝土采用C50,普通钢筋采用HRB335,预应力筋采用高强度低松弛钢绞线直径15.2 mm共计27根,强度标准值为1 860 MPa,桥面铺装采用5cm厚沥青铺装层和9 cm厚C30混凝土。横断面跟T梁断面如图1所示。

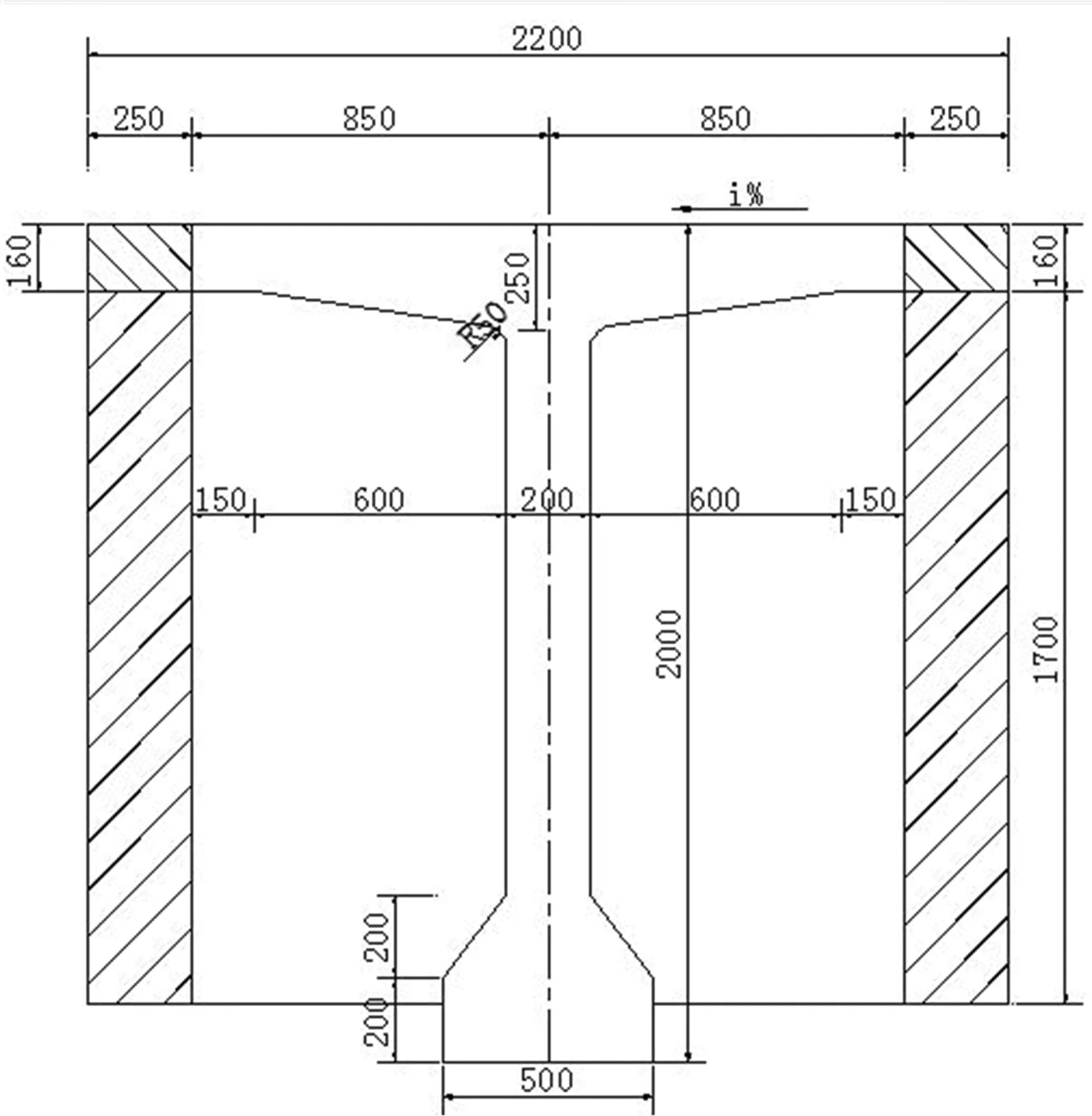
图1 T梁标准截面图(单位:cm)

3.2 混凝土碳化和钢筋初锈时间判定

根据徐善华[3]、王鹏[4]关于混凝土碳化和钢筋初锈时间的研究,得到钢筋初锈时间如下:

K=KmcKjKco2KpKsKeKf=2.1762

(5)

X0=4.86*(-RH2+1.5RH-0.45)×

(c-5)×(lnfcu,k-2.30)=35.5601(mm)

(6)

(7)

3.3 抗力影响因素和车辆荷载

本文选取了对可靠度影响较为显著的几个变量(表1)作为研究对象。

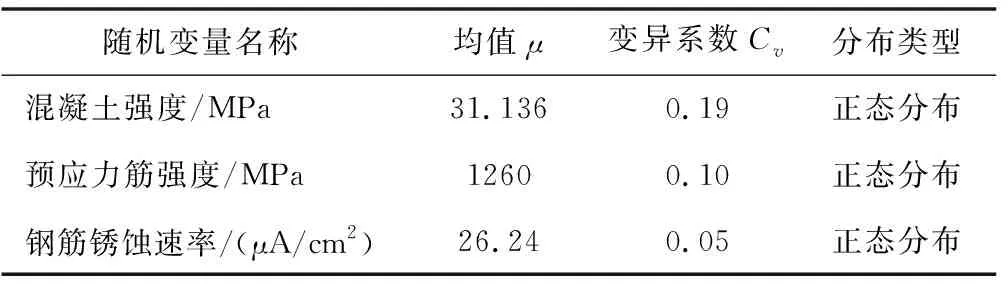
表1 随机变量统计参数表

采用有限元软件MIDAS建立模型，如图2所示,计算各根主梁在车辆荷载下的跨中最大弯矩(表2),主梁编号,如图3所示。

图2 桥梁结构有限元模型

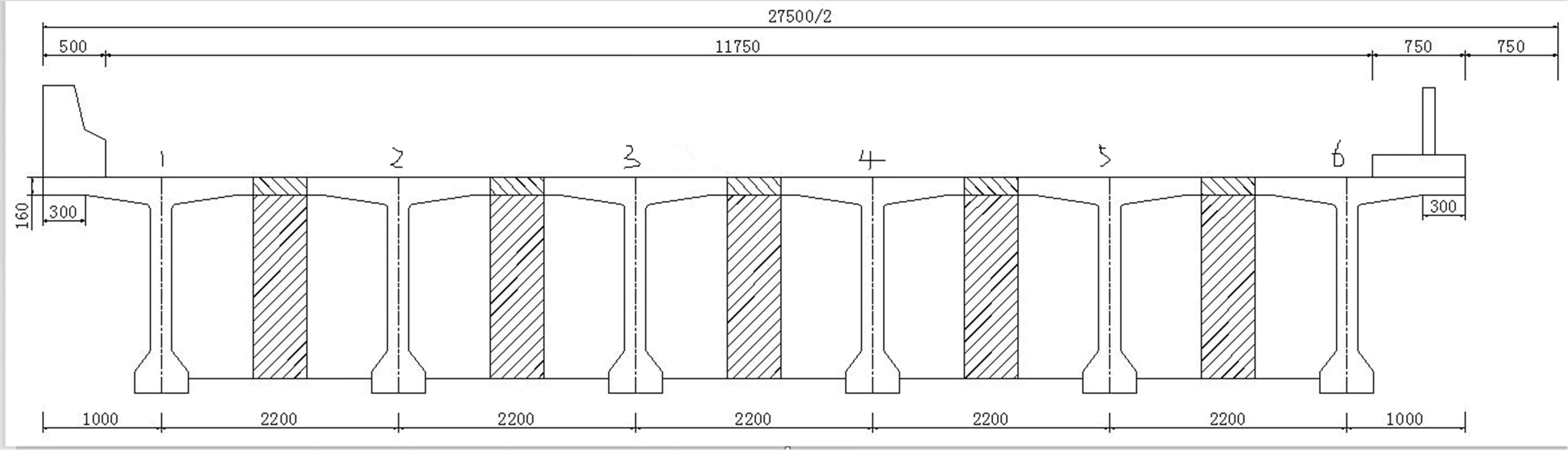
图3 横断面布置图(单位:m)

表2 各主梁车辆荷载下最大弯矩值

3.4 可靠度计算结果

根据《公路工程结构可靠度设计统一标准》[5],二级安全等级桥梁容许可靠度为4.2,将该桥参数代入基于MATLAB编制JC法可靠度计算程序,得到各主梁可靠度进而以串联系统原理计算全桥可靠度,各主梁及全桥可靠度,如图4所示。

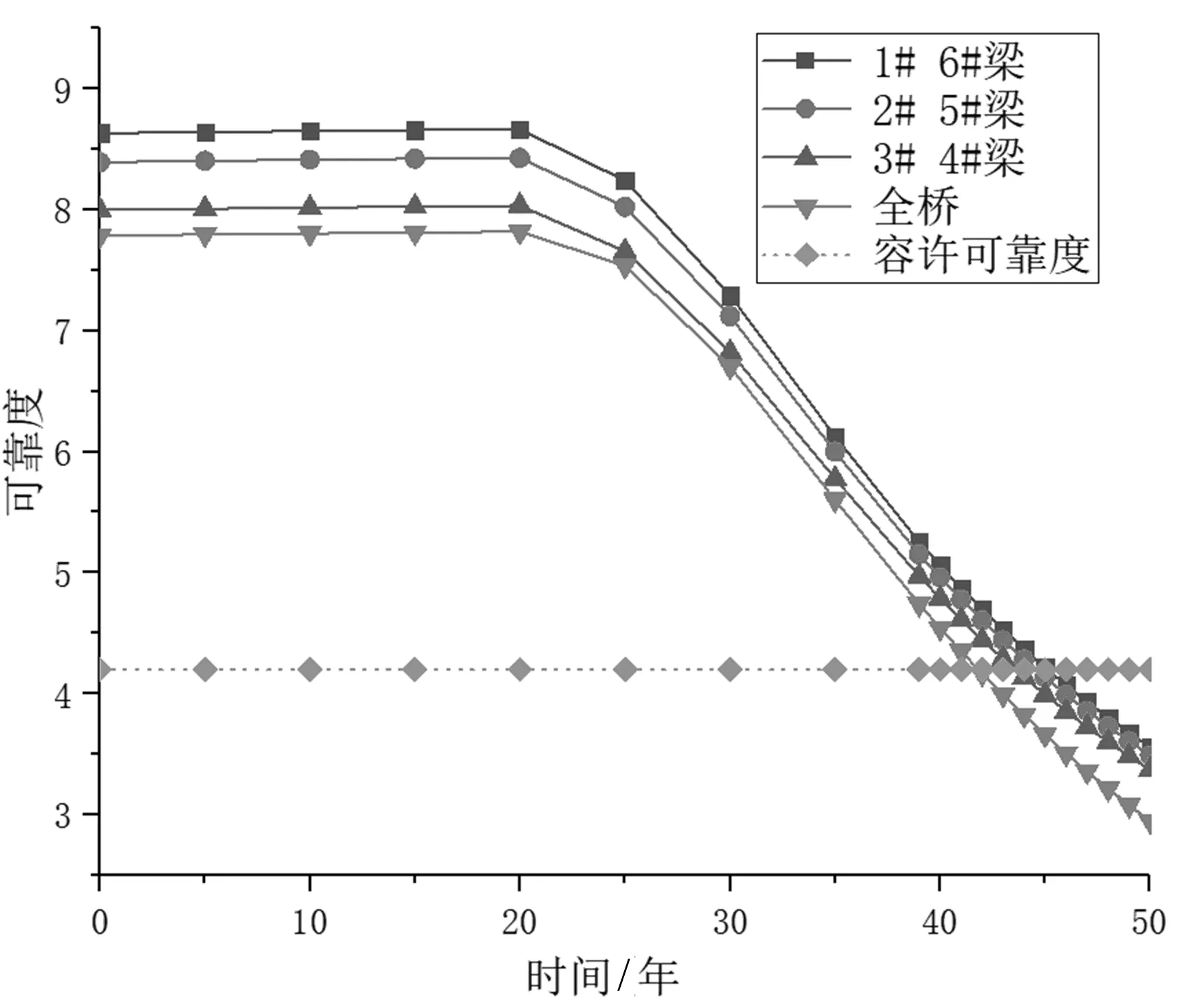
图4 桥梁可靠度时变图

从图4中可以看出,前20年可靠度变化很小,这是因为预应力筋尚未开始腐蚀;20年之后,预应力筋在锈蚀后强度降低,导致结构抗力下降迅速,可靠度下降明显;42年之后,全桥可靠度开始低于容许值,需采取相应维护措施,来保证桥梁在维护期内具有足够性能。

4 多目标维护决策模型

4.1 维护效应模型与维护成本模型

本文考虑采用体外预应力法进行维护,根据彭灿[6]的研究,主梁和边梁所需维护成本和维护效应相差很小,采用他的计算方法和《公路工程概算定额》[7],得到。下面以表3所示单根T梁维护效应和维护成本。

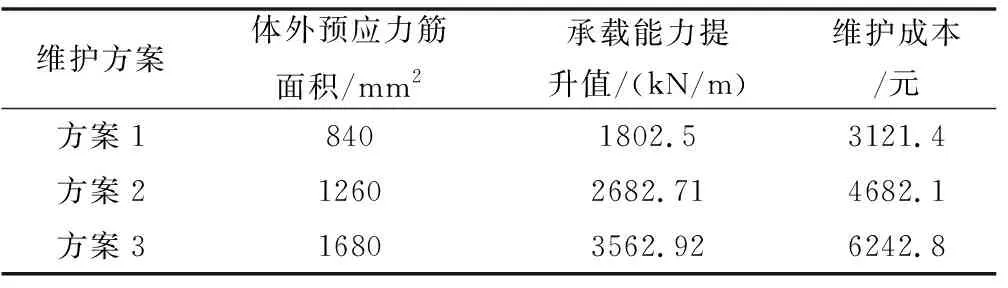
表3 单根T梁维护效应和维护成本

4.2 多目标决策模型

考虑该桥50年维护期进行维护决策优化,以维护成本最低和全桥可靠度最大为目标函数,以全桥可靠度大于容许可靠度指标4.2为约束条件,建立多目标优化模型:

s.t.βi(t)>[βi]

(8)

4.3 非劣解的判定及约束处理

在本例中,将约束处理融入非劣解选取中,对于不等的i、j,若不存在下列的任一项,则保留i为非劣解:

(1)F1(i)F2(j);

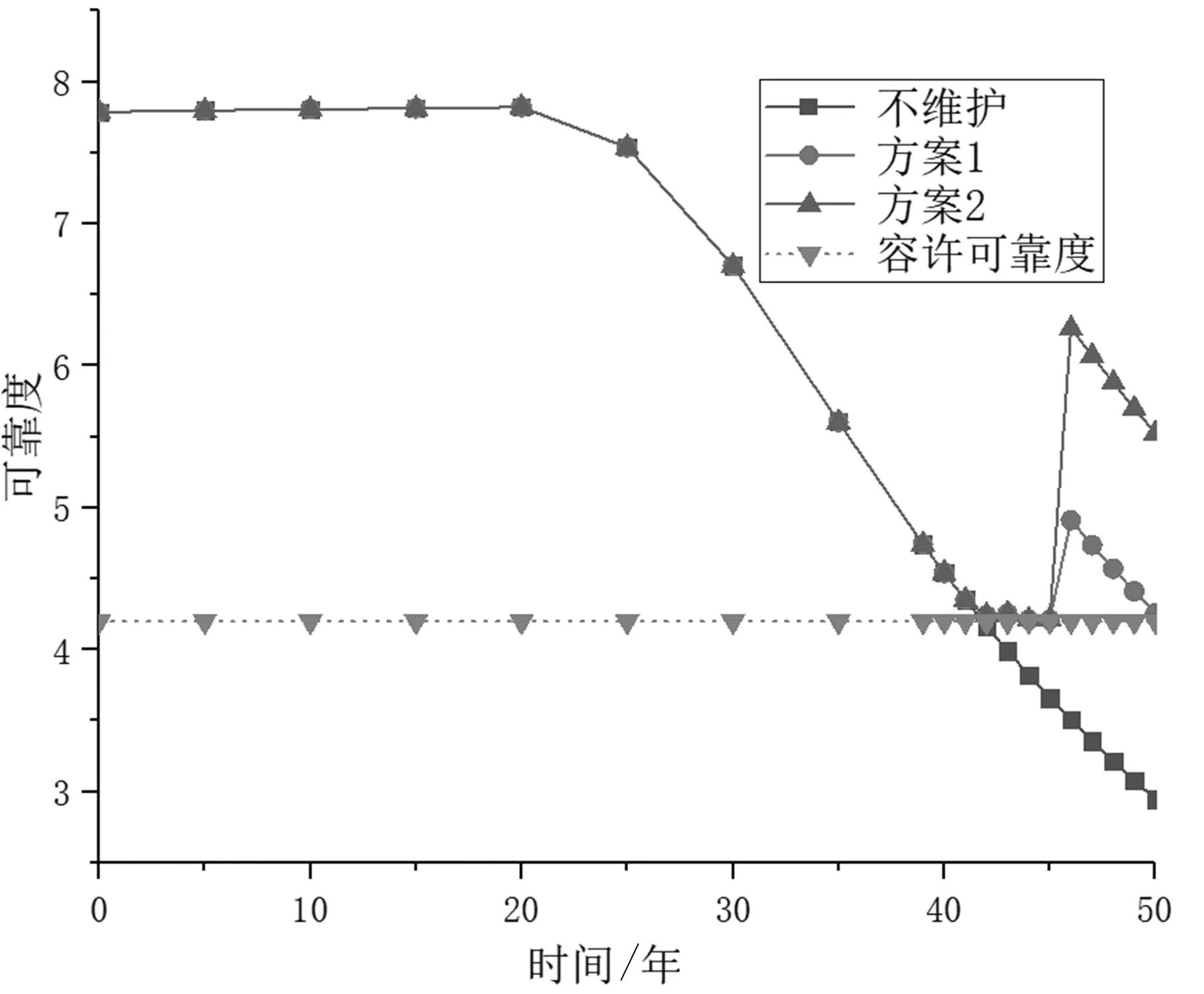
(2)F1(i)

(3)F1(i)=F1(j)&F2(i)>F2(j);

(4)βi(t)<[βi]。

(9)

4.4 维护决策结果

采用 多目标粒子群算法对式(8)进行维护决策优化,维护优化结果如图5所示。

图5 维护优化结果

图5中18个方案(其中两个点图中重复)均为pareto最优解,在这些方案中,不存在任何一个方案与其他方案相比花费维护资金更多而全桥可靠度更低,且均能使桥梁满足容许可靠度要求。下面以方案1和方案2为例,来演示维护后桥梁可靠度变化，如图6所示。

图6 维护后全桥梁可靠度时空图

5 结束语

本文基于可靠度理论,对桥梁的性能进行评定,并在此基础上引入多目标粒子群算法对桥梁维护决策进行优化,使得有限的维护成本效益最大化，得到一系列pareto最优解供管理者参考。本文在进行维护决策优化时,采用的是简支梁桥,其失效模式较为简单且体系可靠度易求得,对于具有更复杂的失效模式和结构体系的桥梁维护决策优化还需进一步研究。