120 MeV电子直线加速器束流准直研究

孙 彬 王 煜 黑东炜 李斌康 谭新建 翁秀峰 刘 军 张小东 付竹明

（西北核技术研究院 强脉冲辐射环境模拟与效应国家重点实验室 西安710024）

基于光阴极微波电子枪的S波段常温直线加速器，可以产生低发射度、低能散、精确时间同步的高品质束流。电子束团在传输过程中，会受到束线上的各种元器件误差的影响，如果束流偏离设计的中心轨道，就会影响束团发射度等参数，为了获得更好的束流参数，应要对束流轨道进行测量和控制。传统机械准直方法的精度通常在百微米量级，难以满足120 MeV电子直线加速器的50 μm以内的准直要求。20世纪80年代逐渐发展起来了一种基于束流的准直技术，该方法不依赖机械测量工具的高度精密性，通过逐个扫描四极磁铁的电流值，配合束流位置检测器（Beam Position Monitor，BPM）的读数，通过计算消除束流轨道和四极铁之间的偏差，使电子束团精准地通过四极铁磁中心，达到减小二极场踢力扰动，抑制发射度增长，在相同电子枪和束线lattice的情况下，使加速器获得更好的束流品质［1-4］。

1 基于束流的准直方法

120 MeV电子直线加速器由光阴极微波电子枪、两段3 m长SLAC型S波段行波加速管、发射度补偿螺线管线圈、加速段螺线管线圈、锁模激光器系统、同步控制系统、三套速调管微波功率源及各类电源和磁铁等组成，如图1所示。电子束设计指标为：电荷量0.1～0.5 nC，归一化发射度＜1.0 mm·mrad，能散＜0.3%（均方根值（Root Mean Square，RMS）），束团长度1～3 ps（RMS）［5］。

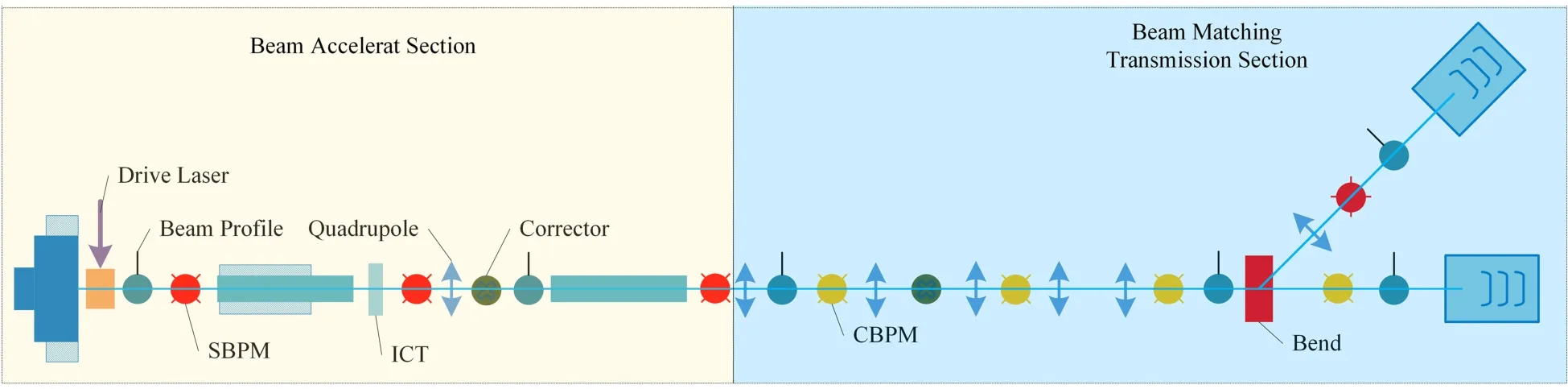
图1 120 MeV电子直线加速器结构Fig.1 Configuration of 120 MeV electron linear accelerator

电子束流轨道受到四极铁磁场、磁铁电源抖动、环境温度和束线局部温度等众多因素影响，如果束流通过四极铁时轨道偏离了四极铁的磁中心，四极铁将对束流产生一个二极分量的作用力，从而给束流轨道带入扰动［6］。为了抑制器件磁中心偏移对束流的作用，基于束流的准直技术是120 MeV电子直线加速器提高束流品质的有效途径之一。

消色散校正法是一种新型的基于束流的准直技术，最早应用于国际直线对撞机（International Linear Collider）上，用来对束流轨道进行控制。该方法相比其他轨道校正算法具有极大的优势，不仅对束流轨道进行控制，还可以减少束流方向上的色散，束流能量变化对轨道影响减小。DFS不但可以计算出四极铁误差，而且还可以求出BPM的电中心误差，采用四极铁电移支架等精密移动装置，可以较好地消除四极铁横向位置误差。该方法已广泛应用于大型直线加速器装置中，例如美国斯坦福直线加速 器 中 心（Stanford Linear Accelerator Center，SLAC）的直线加速器相干光源（Linac Coherent Light Source，LCLS）［7］、瑞士 PSI的 Swiss FEL［8］、德国DESY的FLASH［9］、欧洲的EXFEL［10］等。DFS算法采用改变束流能量代替改变四极铁强度，将束流轨道变化归结到四极磁铁位置偏差，通过对不同能量的BPM数据分析，就可以得到四极铁和BPM的偏移量，其最大优势在于在束流轨道准直的同时，也能将束流能量改变引起的轨道变化消除，其对能量变化不敏感的准直效果在能量可调的直线加速器上是其他准直方法无法比拟的。

使用DFS方法校正束流轨道，需获取不同能量下的相应位置BPM的测量数据，假设横向坐标上只考虑四极铁误差和校正子，第i个BPM的读数如式（1）所示。

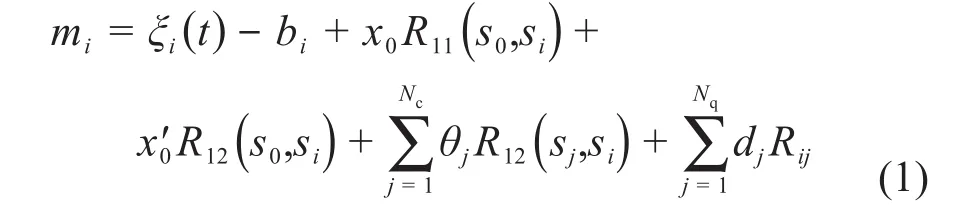
式中：ξ代表BPM的随机误差；θ代表校正子的弯转角度；b和d分别代表BPM和四极铁的理想轨道横向坐标偏差；R11（s0，si）和R12（s0，si）为束线纵向位置s0～si的传输矩阵相应元素，同样的R12（sj，si）为第j个校正子到第i个BPM的传输矩阵的对应元素；Nc和Nq分别代表校正子数量和四极铁数量；Rij是与四极铁横向坐标偏差dj的响应系数，计算方法如式（2）所示。

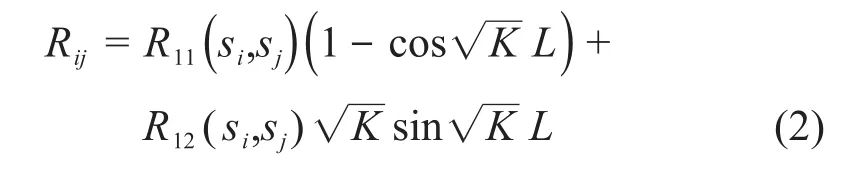
式中：K为第j个四极铁的归一化强度，K=(e/βγmc2)dBy/dx；有效长度 L；四极铁出口位置为 sj，当si＜sj时，Rij=0。

当调节上游加速管微波功率源高压，BPM读数的变化量Δmi表示为：

不考虑其他误差的影响，比如BPM精度、功率源抖动或者磁铁强度误差等，可以列出下面的矩阵，假设有M个四极铁和N个BPM：

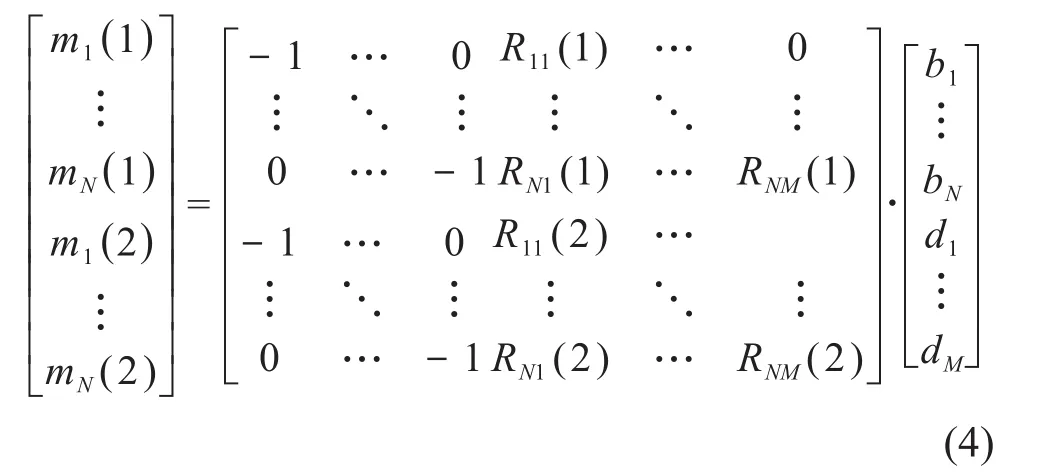
式中：mi（k）代表第k次能量的第i个BPM的读数；Rij(k)代表第j个四极铁偏差对第i个BPM读数的响应系数，bi和dj分别代表第i个BPM和第j个四极铁偏差［11-12］。通过计算获得四极铁和BPM的横向位置误差，调整四极铁位置使束流通过四极铁中心。在计算中，需根据具体情况添加软约束条件，可以较好地解决四极铁个数总是大于BPM个数带来的方程解有可能远大于0的问题，其定义为：

式中：si代表第i个四极铁的位置；Δqi代表第i个四极铁的横向位置误差，经过几次重复操作，就可以实现束流匹配段的高精度准直。

2 模拟计算结果

在120 MeV电子直线加速器轨道准直主要对束流匹配段（即图1右侧区域，如图2所示）准直。束流匹配段拟采用消色散校正法，束流匹配传输段由4个四极铁、4个四极铁电控移动平台、4个腔式束流位 置 检 测 器（Cavity Beam Position Monitor，CBPM）、一个校正子组成（图3），使用的条带式BPM的位置分辨率为10 μm@0.5 nC，腔式BPM的位置分辨率为1 μm@0.5 nC。

四极铁平移台由两套滑台组成：水平滑台和斜滑台机构，可以实现水平和高度两个方向上的位移调节，均采用光栅尺读数反馈闭环控制，调节精度和重复性误差≤±3 μm，移动范围为3 mm。迄今为止，DFS算法应用场景主要为高能电子加速器上，电子束能量均在GeV级别，例如ILC中心能量150～250 GeV，FLASH 0.37～1.25 GeV，对于120 MeV以下的中低能加速器应用较少。影响DFS算法效果的因素有非线性、BPM精度、束流抖动、磁铁尺度误差、射频抖动等［10］，在较低能量下束流抖动和磁铁尺度误差会比高能量时更大。结合加速器运行情况，使用Mad-X软件对DFS算法进行模拟计算。

120 MeV电子直线加速器元件横向准直误差，螺线管约80 μm，四极铁约100 μm，BPM约200 μm，各项元器件误差均会反应在下游BPM测量的数据上。根据加速器实际运行情况，测量了在匹配传输段入口处SBPM的数据作为束流抖动情况，测量数据的抖动是束流抖动和测量误差共同作用的结果，如表1所示。

图3 CBPM和四极铁电移支架Fig.3 CBPM and quadrupole mover

表1 束流在不同能量下测量得到的抖动测量情况Table 1 Beam jitter in different energy

图4 束流匹配段各四极铁和CBPM代号Fig.4 Code name of quadrupole and CBPM in linac beam matching section

120 MeV电子直线加速器没有为每块四极磁铁出口都配备了相应的BPM，所以只能进行分两组校正 ，｛Quad1M，CBPM2，Quad3M，CBPM3｝和｛Quad2M，CBPM2，Quad4M，CBPM3｝，在一组进行校正时，另外两块四极铁电源关闭。

以第一组校正为例，按测量数据给定模拟误差Quad1M的x方向位置误差为100 μm，Quad3M的误差-80 μm，CBPM2的误差为-120 μm，CBPM3 的误差为 150 μm，束流扰动在～25 μm、15 μm、12 μm、9 μm、6 μm的情况下的DFS算法校正计算结果如图5所示，每次迭代计算20次。

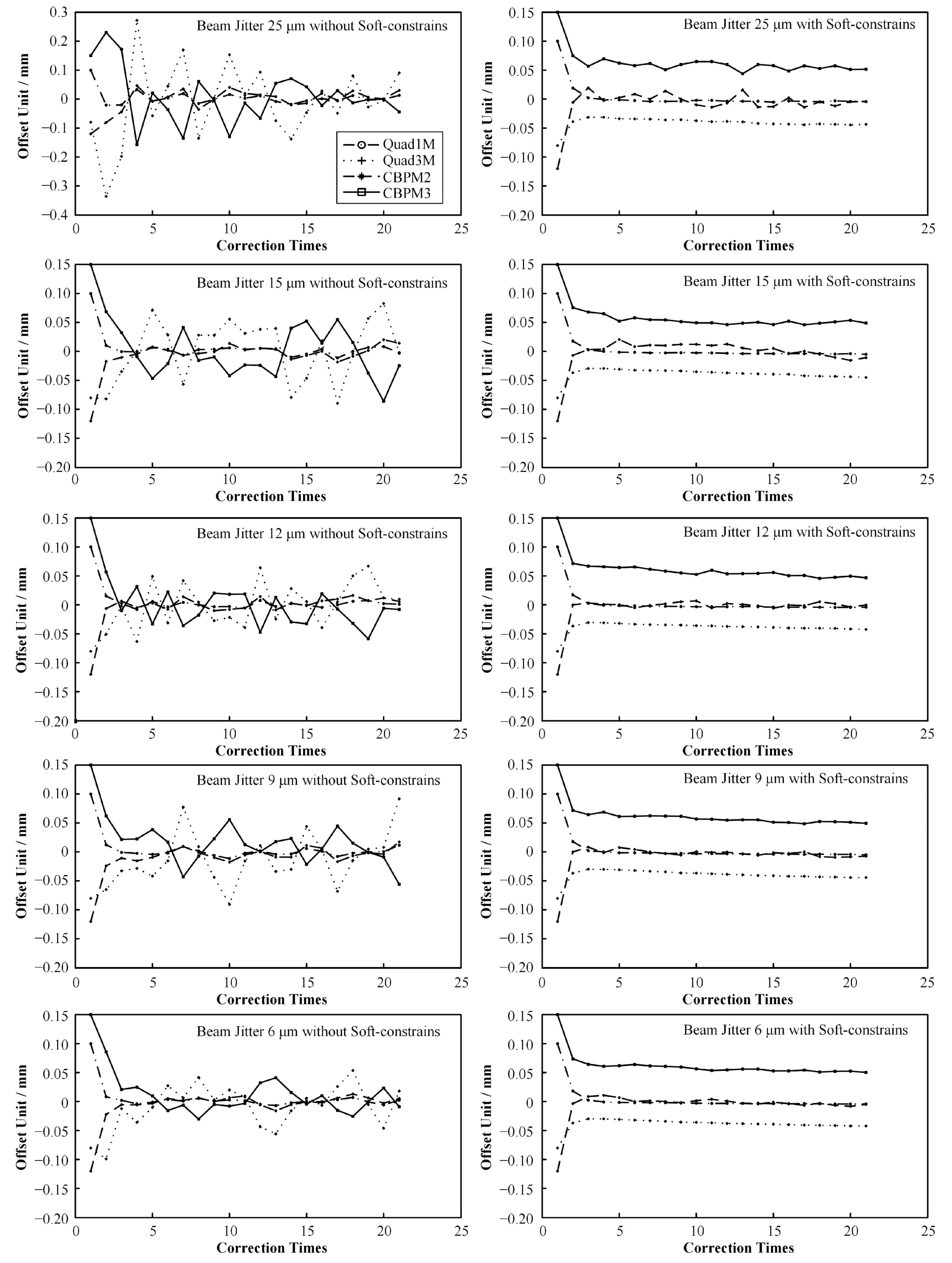
图5 不同束流扰动情况下（25 μm、15 μm、12 μm、9 μm、6 μm）DFS算法的模拟实验结果Fig.5 Simulation result of DFS in different beam jitters(25 μm、15 μm、12 μm、9 μm、6 μm)

在束流扰动为9 μm以上的情况下，算法在不加软约束的情况下难以收敛，所以120 MeV电子直线加速器使用DFS算法在下游设备Quad3M、CBPM3上难以得到较好的准直效果。当算法增加软约束条件情况下，算法鲁棒性提高明显，在25 μm束流扰动的情况下依旧可以收敛，但是增加软约束以后，算法在低束流抖动的情况下收敛结果比未加软约束的情况下差。模拟计算结果表明：对于120 MeV电子直线加速器，DFS算法可以较好地进行在线束流准直工作，同时根据束流实际抖动情况，选择是否增加软约束可以提高准直效果和精度，具体模拟计算数据如表2所示。

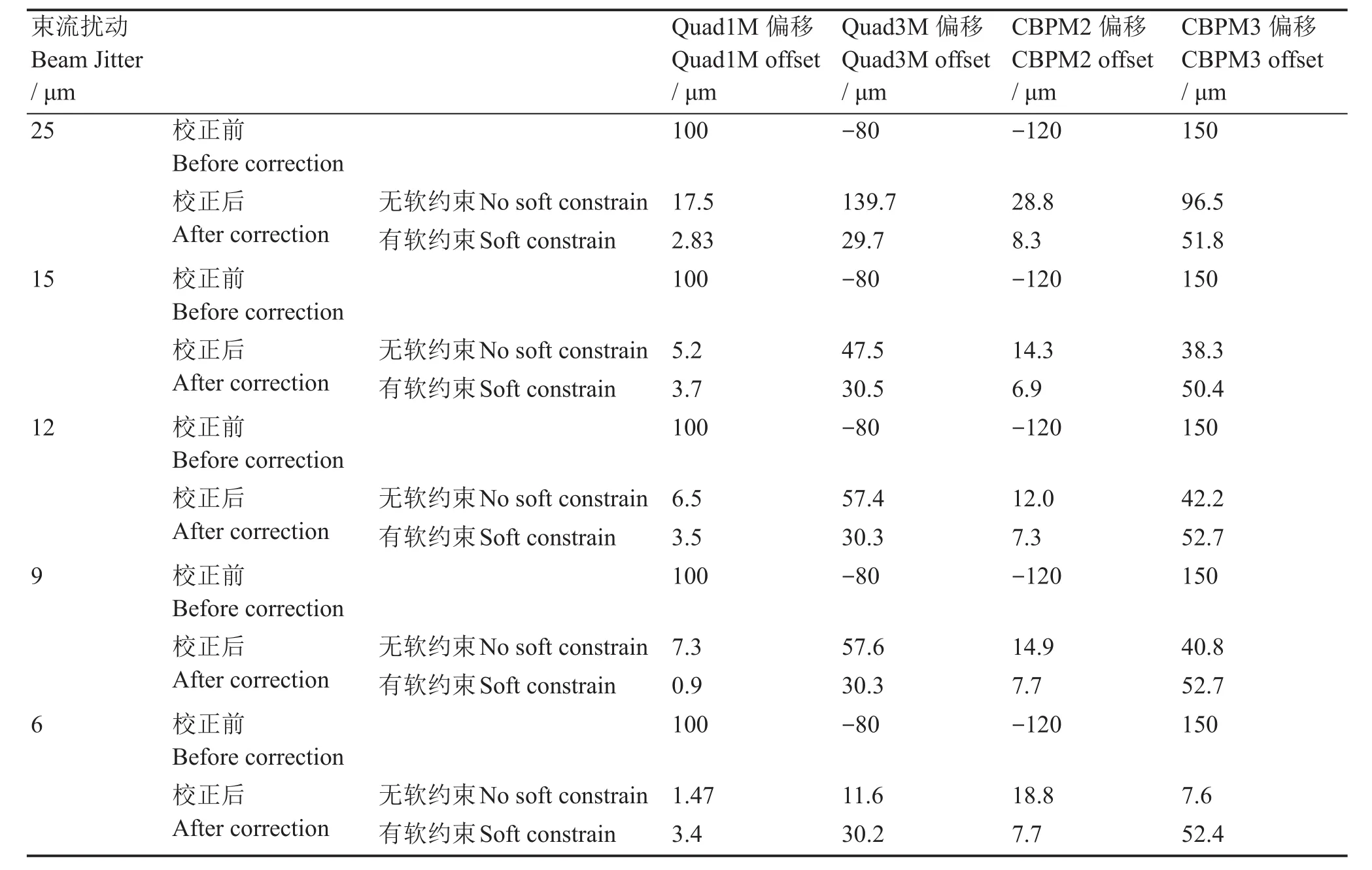
表2 经过DFS算法校正后四极铁和BPM的中心偏移Table 2 Quadrupole and BPM center offset after correction

3 结语

本文给出了120 MeV电子直线加速器进行BBA准直的设计方案，通过模拟计算表明了DFS算法在对于120 MeV能量可调电子直线加速器装置有很好的效果，将四极铁和BPM的准直误差由百微米降低到50 μm左右，四极铁移动器对四极铁位置进行调整减少了束线中校正子的数量，DFS算法减小了四极铁中心偏差和校正子二极场带来的色散误差，有效提高了末端束流品质。模拟计算为下一步在120 MeV能量可调直线加速器应用DFS算法进行束流准直工作和加速器下一步能量升级工作打下了良好的基础。