基于组件计算的燃耗实验基准题建模分析

汪天雄 张滕飞 吴海成 刘晓晶 熊进标 柴 翔

1（上海交通大学核科学与工程学院 上海 200240）

2（中国原子能科学研究院核数据重点实验室 北京 102413）

多群数据库是核工程科学计算的基础数据来源，其合理性将直接影响数值模拟的精度。采用实验数据开展多群数据库的验证和确认［1］，能够大幅提高所建立多群数据库的可信度。SFCOMPO-2.0［2-3］（Spent Fuel Isotopic Composition Database）是经济合作与发展组织（Organisation for Economic Co-operation and Development，OECD）核 能 机 构（Nuclear Energy Agency，NEA）实验分析测量数据库的最新版本，现已被广泛用于核安全分析、乏燃料后处理及优化、堆芯设计领域。该数据库包含了8种不同堆型、44座反应堆、750个乏燃料样品的堆芯、组件及栅元信息，以及其破坏性放射化学分析得到的主要核素浓度数据。SFCOMPO-2.0数据库为反应堆物理组件程序的校核提供了有力的验证工具，如Bamidele Ebiwonjumi等基于此数据库开展了STREAM程序的验证校核［4］。

MOX（Mixed Oxide Flue）燃料的使用有利于提高核燃料的利用率，减少核废料，已成为乏燃料后处理及新型堆芯设计的主要研究方向。为了应对研发MOX燃料和可燃毒物多群常数库的需求，有必要建立该多群常数库的燃耗基准实验计算例题，用于该库的燃耗基准检验。本工作从SFCOMPO-2.0数据库中选取H.B.Robinson-2压水堆、Beznau-1压水堆及Takahama-3三种压水堆的燃耗基准实验，采用DRAGON组件程序［5-6］构建二维单栅元模型［4］，并利用转化关系将模拟结果与实验值进行对比和分析，从而为MOX燃料和可燃毒物多群常数库燃耗基准检验奠定基础。

1 计算模型

本 文 选 择 了 Takahama-3、Beznau-1、H.B.Robinson-2三座反应堆的试验样品进行建模计算。试验样品的乏燃料核数组分可通过SFCOMPO 2.0数据库查询。

针对不同反应堆试验样品，分别建立了对应单栅元计算模型，计算模型边界条件均设置为全反射边界条件，如图1所示。其中，单栅元计算模拟忽略了燃料芯块与燃料包壳间的气隙。经敏感性分析，气隙结构并不会对模拟结果的精度造成明显影响，因此在后续的计算过程中忽略了气隙区域以提高计算效率。

首先选取了Takahama-3反应堆的SF95、SF97系列样品，燃料类型为UO2。燃料棒包壳外径为9.5 mm，内径为8.22 mm，燃料芯块直径为8.05 mm。

图1 单栅元计算模型Fig.1 Pin cell model

Beznau-1反应堆本文模拟所选取的样品点分别位于M109和M308燃料组件，燃料类型为MOX燃料，M108组件包含D3、B6系列样品，M308组件包含K7系列样品。组件程序采用单栅元计算模型模拟D3、B6、K7系列样品。其中，包壳外半径为0.536 cm，包壳内半径为0.474 cm，燃料区域半径为0.464 6 cm，栅元边长为1.412 cm。

H.B.Robinson-2反应堆模拟样品点分别位于BO-5燃料组件的P8、N9、E14燃料棒之上，燃料类型为UO2。其中，包壳外半径为0.535 cm，包壳内半径为0.473 cm，燃料区域半径为0.465 cm，栅元边长为1.43 cm。

实际堆芯运行中，慢化剂中的硼浓度随燃耗的变化数据可以在SFCOMPO-2.0数据库中查询。为了提高计算精度，我们在计算过程中对燃耗步进行了细分，而对于未给出硼浓度的燃耗点采用线性插值的手段得到对应的硼浓度值。线性插值假设在已知两个时间点间，硼浓度随时间线性变化，而实际情况下，硼浓度随时间的变化可能是非线性的。这会导致建模计算中插值计算得到的硼浓度与实际情况存在一定偏差。

在计算中，每一步计算采用的燃耗值根据SFCOMPO-2.0数据库给出的功率变化时间点定义。值得注意的是，不同燃耗点下不光存在燃耗值的区别，慢化剂的材料及功率密度也相应地有所变化。以Takahama-3反应堆为例，表1列出了SF95样品点的燃耗信息。其中，Sample-1、Sample-2、Sample-3等表示SF95燃料元件轴向不同位置的测量点。

2 数值结果

在计算过程中，我们首先对比了DRAGON程序中两种不同的核数据库（WIMS-D4 69群和WIMSD4 172群）对于计算结果的影响。该数据库是经过检验的权威数据库，被广泛应用，能够满足三种压水堆燃耗计算的要求。计算结果表明：两种数据库对于计算精度的影响可以忽略。因此，在后续的模拟计算过程中统一选取WIMS-D4 172群数据库进行计算。对几何模型进行网格剖分，为了平衡计算效率及计算精度，经过敏感性分析，选取燃料棒内部平均划分16个平源区、包壳平均划分为两个平源区、冷却剂划分为三个平源区的网格剖分方案，具体如图2所示。最后，对不同燃耗步划分方式进行敏感性分析，确定了用于计算的燃耗步划分方案，表2列出了以Takahama-3反应堆SF95系列样品的燃耗步划分。本文后续核素的核子密度计算统一基于网格敏感性分析及燃耗步敏感性分析的结果。

计算结果与SFCOMPO-2.0数据库实验基准值对比结果整理成图表。其中表3为SF95-Sample-2的计算结果，图3为相对偏差柱状图。结果表明：234U与235U的相对偏差分别为-8%和12%。238Pu、239Pu、241Pu、241Am、242mAm、154Eu、106Ru、125Sb的相对偏差超过20%。242Pu相对偏差为11%。其余核素偏差均在10%以内。

由于234U可通过（n，γ）反应产生235U，计算程序中234U的（n，γ）反应截面与实际值的偏差可能是造成234U计算存量小于实际存量的原因，而235U计算存量相比于参考值偏高可能是由于模拟计算燃耗深度与实际燃耗深度的不匹配导致的。238Pu通过一系列（n，γ）反应生成241Pu，而241Pu可通过辐射俘获反应生成242Pu，亦可通过β-衰变生成241Am，241Am可通过中子俘获反应生成242mAm。由于本研究中燃耗计算采用了组件的平均功率作为输入功率，不可避免与实际运行的功率存在偏差，燃耗计算的功率小于实际功率可能造成242Pu核素计算值小于实验值，241Am、242mAm计算值高于实际值。242Cm通过α衰变产生238Pu，而238Pu可通过辐射俘获反应产生239Pu，计算程序中242Am经过中子俘获反应生成242Cm偏多，可能导致242Cm衰变产生238Pu增多。154Eu由153Eu通过中子俘获反应产生，其消失路径包括β-衰变产生154Gd及通过中子俘获反应生成155Eu，而燃耗计算中中子通量密度会影响154Eu存量。106Ru通过裂变产出及105Ru通过中子俘获产生，消失途径包括中子俘获反应及β-衰变。106Ru存量与裂变碎片产额及中子通量密度有关，106Ru计算裂变产额大于实际裂变产额或中子通量密度小于实际中子通量密度可能导致其计算结果大于实验值。144Nd由144Ce β-衰变产生的144Pr经β-衰变产生。144Ce计算偏差为-6%，这可能造成144Nd与实验值偏差-10%。125Sb核素裂变产额大于实际裂变产额可能导致其计算结果与实验值偏差较大，且125Sb存量较小，基准实验值的不确定性较大也可能会加剧这样的偏差。

图2 空间网格剖分Fig.2 Mesh generation for calculation

表2 SF95样品燃耗步划分Table 2 Depletion calculation steps of SF95 sample

图3 Takahama-3-SF95-Sample-2计算结果相对偏差Fig.3 Schematic of relative deviations for Takahama-3-SF95-Sample-2

SFCOMPO-2.0数据库提供的H.B.Robinson-2反应堆乏燃料组分参数，仅包括铀和钚及其同位素以及148Nd核素的存量信息。表4为H.B.Robinson-2反应堆Sample A计算结果，图4为相对偏差图。结果表明：235U、239Pu、241Pu、242Pu相对偏差超过10%，且最大偏差不超过25%。其余核素偏差均在10%以内。

计算结果中148Nd核素存量相对偏差为-1%，表明实际燃耗深度大于计算燃耗深度，这可能是235U核素计算存量大于基准值且相对偏差大于10%的原因。239Pu、241Pu及242Pu核素燃耗计算存量对计算燃耗历史有较大的敏感性。通过SFCOMPO-2.0数据库得到的计算程序的燃耗历史可能存在较大偏差，这可能是239Pu、241Pu及242Pu核素计算结果存在较大相对偏差的原因。

表5为Beznau-1反应堆Sample BM1计算结果，图5为计算结果相对偏差。从图5可以发现，236U、238U、238Pu、137Cs、144Nd、145Nd、148Nd核素相对偏差在10%以内，其余核素相对偏差均超过10%。

其中，234U相对偏差为-86%，235U相对偏差为19%，148Nd核素相对偏差为9%。234U核素在初始MOX燃料和乏燃料中存量均较小，存在较大的不确定度，可能是造成234U计算结果与基准值存在较大偏差的原因。而148Nd、235U及239Pu核素计算结果均大于基准值，可能是由于实际MOX燃料初始组分与计算程序的组分不同引起的。106Ru通过裂变产生及105Ru通过中子俘获反应产生，消失途径包括中子俘获反应及β-衰变。106Ru存量与裂变碎片产额及中子通量密度有关，106Ru计算裂变产额小于实际裂变产额或中子通量密度大于实际中子通量密度可能导致其计算结果小于实验值。

表3 Takahama-3-SF95-Sample-2计算结果与基准实验值对比Table 3 Comparisons with experimental data for Takahama-3-SF95-Sample-2

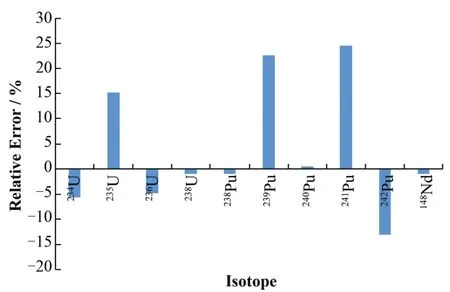
图4 H.B.Robinson-2-SampleA计算结果相对偏差Fig.4 Schematic of relative deviations for H.B.Robinson-2-SampleA

表4 H.B.Robinson-2-SampleA计算结果与基准实验值对比Table 4 Comparisons with experimental data for H.B.Robinson-2-SampleA

表5 Beznau-1-Sample BM1计算结果与基准实验值对比Table 5 Comparisons with experimental data for Beznau-1-Sample BM1

上述三座反应堆样品模拟计算结果表明，234U、235U与实验值有一定偏差。实际234U与中子的234U（n，γ）235U反应截面与计算程序中的截面不同可能是造成这种偏差的原因。此外，234U在新燃料中含量很低，对234U初始含量的确定带有较大的不确定性，这也可能导致计算结果产生偏差。在计算程序燃耗链中均未考虑234U及235U两种核素（n，2n）反应以及自身的α衰变反应，这是可能造成235U核素模拟结果均高于实验值的系统偏差。计算燃耗功率与实际燃耗功率偏差可能导致一些对燃耗计算功率敏感的核素的计算结果与实际有一定偏差，如：238Pu、239Pu、240Pu、241Pu、242Pu、241Am等。计算程序中125Sb核素裂变产额大于实际裂变产额可能导致其计算结果与实验值偏差较大。

图5 Beznau-1-Sample BM1计算结果相对偏差Fig.5 Schematic of relative deviations for Beznau-1-Sample BM1

3 结语

本文基于单栅元模型对SFCOMPO-2.0燃耗实验基准题中Takahama-3反应堆的SF95-sample-2样品、H.B.Robinson-2反应堆中Sample A样品及Beznau-1反应堆中的Sample BM1样品进行了计算、对比和分析。结果表明：多数核素的模拟结果与实验值吻合较好。同时，Sample BM1相比于其他两种样品计算得到的U元素和Nd元素的相对偏差均偏大。由于Sample BM1燃料棒所处的周边环境更加复杂，造成Sample BM1样品点周围中子通密度畸变，因此单栅元计算模型无法精确模拟样品点周围中子通量密度变化可能是造成Sample BM1样品计算结果与实验值偏差更大的原因。采用全组件模型的数值验证是未来的研究方向之一。此外，计算结果表明：Pu、Am、Cs、Eu、Ce、Sb、Ru核素相比其他核素偏差偏大，这一方面是由于这些核素存量较小，导致其计算结果对燃耗历史较为敏感。实际燃耗历史与模拟计算燃耗历史的差异，可能是导致计算结果偏差波动较大的原因。