在“操作”中建构“规律”——《三角形的内角和》教学

吉守兵 蔡金林

【探学内容】

苏教版四年级下册第78、79 页。

【探学过程】

一、探学铺垫

1.出示动态结构图。

（动态呈现“点”——“射线”——“平角”——“钝角”——“直角”——“锐角”——“三角形”）

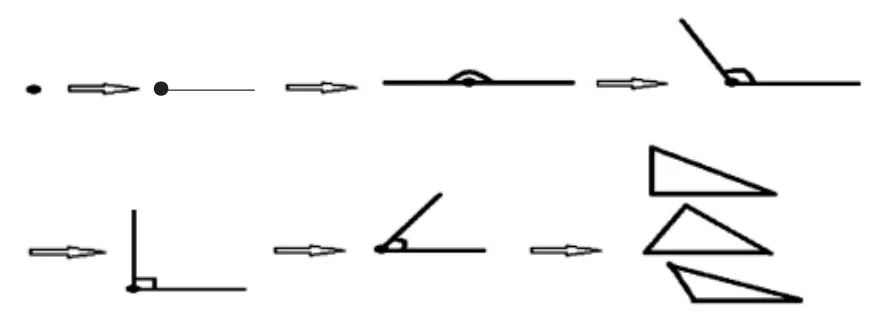
图1

师：仔细观察，把你的发现分享给大家。

生：我发现由“点”引出射线，引出180°的“平角”，变成一个“钝角”，又变成一个90°的“直角”，再变成一个“锐角”。

师：猜一猜这个锐角有多少度？到底是多少度？有什么办法呢？

生：用量角器量一量。（学生用量角器量出锐角度数，并介绍量的方法）

师：（由“角”变成三个不同的“三角形”）这还是角吗？

生：三角形。

2.建立“内角”概念，引入课题。

师：今天，我们从角的角度进一步认识三角形。

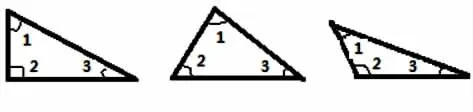
图2

师：为了方便研究，我们把三角形的三个角标上符号，用∠1、∠2、∠3 来表示，这三个角都在三角形的内部，我们把它叫做三角形的三个内角。你认为三角形的内角和指什么呢？

生：三角形三个内角的度数和，就是∠1+∠2+∠3 的度数和。

师：下面我们就一起来研究三角形的内角和。（板书课题：三角形内角和）

二、探究学习

1.从特殊开始，引发猜想。

●研究三角尺上的三角形内角和。

探学要求：

（1）指一指：每块三角尺上的三个内角。

（2）说一说：三角尺上每个内角的度数。

（3）算一算：每块三角尺上三个内角的度数和。

（学生按活动要求独立操作）

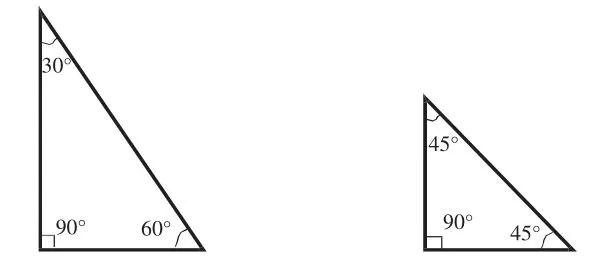
图3

生：第一块三角尺上三个内角是90°、60°和30°，90°+60°+30°=180°。

生：第二块三角尺上三个内角是90°、45°和45°，90°+45°+45°=180°。

●研究两块三角尺拼成的三角形内角和。

师：这两块三角尺都有一个角是直角，通过计算，内角和都是180°。如果把两个这样的三角尺拼起来，拼成的大三角形内角和是多少呢？

探学要求：

（1）拼一拼：用两个同样的三角尺拼成一个较大的三角形。

（2）标一标：标出拼成的较大三角形的每个内角的度数。

（3）算一算：算出拼成的较大三角形的内角和。

（学生按要求自试自探）

师：请小组内交流，做好分享准备。

图4

生：我是这样拼的，拼成的大三角形的三个内角都是60°，60°+60°+60°=180°。

生：我是这样拼的，拼成的大三角形的三个内角是120°、30°和30°，120°+30°+30°=180°。

师：关于三角形的内角和，我们举了三角尺的例子，通过计算这两个三角形的内角和等于180°，而两个相同的三角尺拼起来的大三角形内角和也等于180°，那其他的三角形内角和会是多少度呢？请你们猜一猜。

生：我猜其他三角形的内角和也是180°。

2.由特殊到一般，验证猜想。

师：同学们都认为其他三角形的内角和也都是180°。这是大家根据特殊三角形得到的一个猜想。（板书：猜想 三角形的内角和等于180°？）

师：猜想是我们学习研究的开始，猜想对不对，还需要我们进一步的验证。（板书：验证）

师：请看这三个三角形，不知道它们的度数，就不能像刚才那样，通过已知的度数算出来了，请你想办法验证你的猜想。

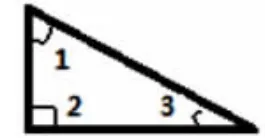
图5

图6

图7

探学要求：

（1）想一想：独立思考验证三角形内角和是180°的方法。

（2）选一选：任选一个三角形操作。

（3）做一做：按自己思考的方法操作，并把过程写在《探学单》里。

（4）说一说：验证的方法。

（学生自主探寻验证三角形内角和是180°的方法。自试自探）

师：请把你们验证三角形内角和是180°的方法在组内进行交流。（实施第一次互助互探）

（学生组内交流后，教师呈现预设资源或学生生成的有效资源1）

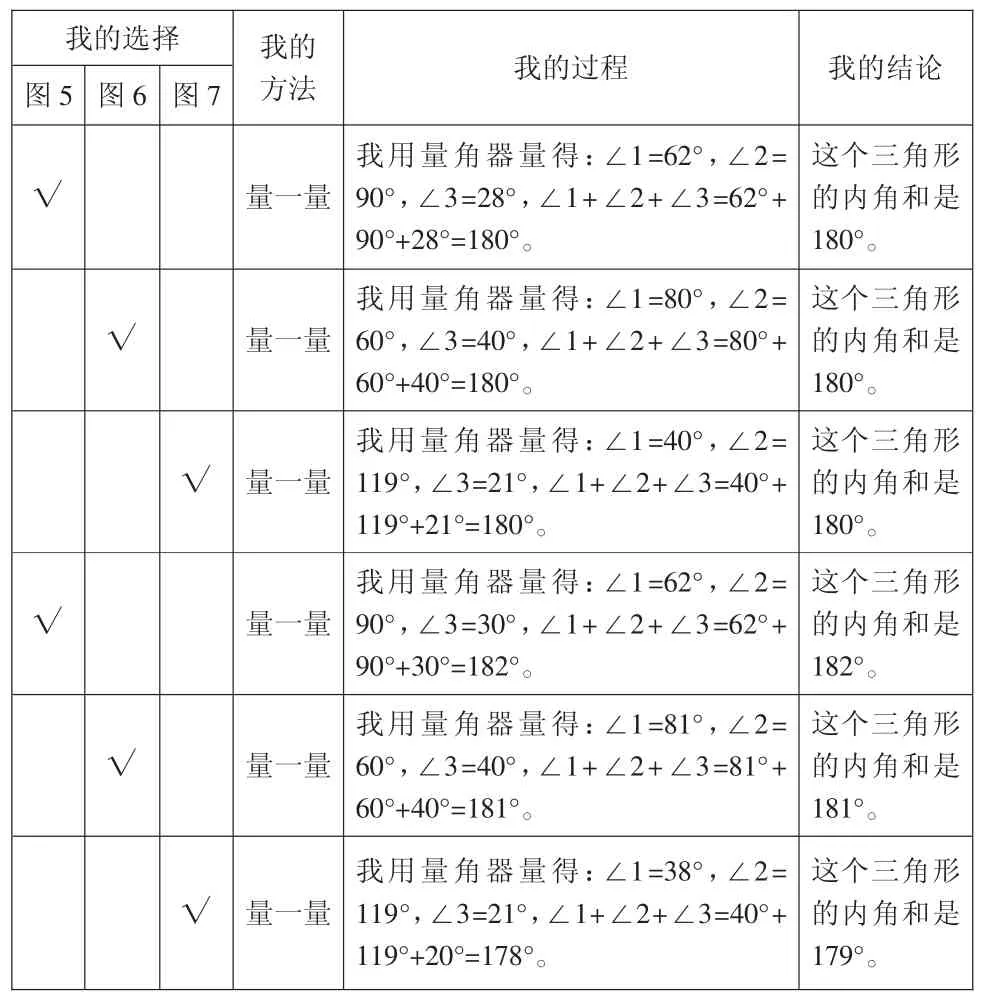
我的选择我的方法我的过程我的结论图5 图6 图7√量一量我用量角器量得：∠1=62°，∠2=90°，∠3=28°，∠1+∠2+∠3=62°+90°+28°=180°。这个三角形的内角和是180°。√量一量我用量角器量得：∠1=80°，∠2=60°，∠3=40°，∠1+∠2+∠3=80°+60°+40°=180°。这个三角形的内角和是180°。√ 量一量我用量角器量得：∠1=40°，∠2=119°，∠3=21°，∠1+∠2+∠3=40°+119°+21°=180°。这个三角形的内角和是180°。√量一量我用量角器量得：∠1=62°，∠2=90°，∠3=30°，∠1+∠2+∠3=62°+90°+30°=182°。这个三角形的内角和是182°。√量一量我用量角器量得：∠1=81°，∠2=60°，∠3=40°，∠1+∠2+∠3=81°+60°+40°=181°。这个三角形的内角和是181°。√ 量一量我用量角器量得：∠1=38°，∠2=119°，∠3=21°，∠1+∠2+∠3=40°+119°+20°=178°。这个三角形的内角和是179°。

师：我们来看看他们是怎么做，怎么想的呢？在组内再次交流。（实施第二次互助互探）

师：请把你们组内交流的结果与全班同学分享吧。（实施交互群探）

生：他们都是用量一量的方法，先分别量出三角形三个内角的度数，再算出三个内角的和。我发现得出的三个内角的和有的是180°，有的比180°多一点，有的又比180°少一点，这是什么原因呢？

生：可能是我们测量方法的问题，也可能是我们测量后读数的问题，造成测量结果的误差。

师：测量的方法会有误差，还不能正确的验证我们的猜想。那有没有更好的方法来验证我们的猜想呢？

（教师呈现预设资源或学生生成的有效资源2）

师：请看这些同学的方法，在组内交流。（实施第三次互助互探）

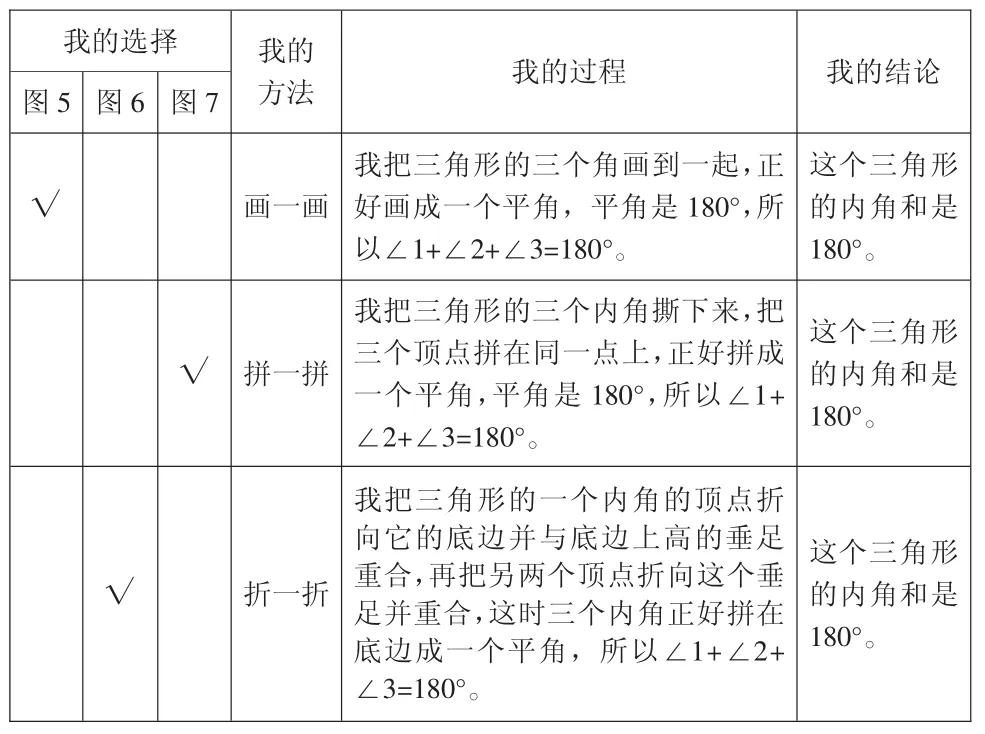
我的选择我的方法我的过程我的结论图5 图6 图7√画一画?我把三角形的三个角画到一起，正好画成一个平角，平角是180°，所以∠1+∠2+∠3=180°。这个三角形的内角和是180°。√ 拼一拼我把三角形的三个内角撕下来，把三个顶点拼在同一点上，正好拼成一个平角，平角是180°，所以∠1+∠2+∠3=180°。这个三角形的内角和是180°。√折一折我把三角形的一个内角的顶点折向它的底边并与底边上高的垂足重合，再把另两个顶点折向这个垂足并重合，这时三个内角正好拼在底边成一个平角，所以∠1+∠2+∠3=180°。这个三角形的内角和是180°。

师：现在，请把你们组内交流的结果分享给大家。（实施交互群探）

生：画一画的方法，把图5 三角形的三个内角画在一起，正好得到一个平角，平角是180°，说明这个三角形的内角和是180°。我认为三个三角形，三个内角画在一起，都能得到一个平角。

生：拼一拼的方法，把图5、图6、图7 任意一个三角形的三个内角撕下来，把三个顶点拼在同一点上，也正好得到一个平角，平角是180°，所以这个三角形的内角和是180°。

生：我觉得拼的时候三个内角既不能有重叠，边与边之间又不能有缝隙。

生：折一折的方法，应该是把图6 三角形任意一个内角的顶点折向它的底边，再把另两个顶点折向这个顶点，这时三个内角正好拼在底边成一个平角，就验证这个三角形的内角和是180°。

生：要先找一个内角对边上高的垂足，然后再把这个顶点折向底边并与底边上高的垂足重合……

生：我发现图5、图6、图7 三种三角形都可以通过画一画、拼一拼、折一折的方法，把三个内角拼到一起，构成一个平角，验证三角形的内角和是180°。说明三角形的内角和是180°。

师：刚才，验证的是老师提供给你们的三角形，通过验证，这三个三角形内角和的确是180°。现在请拿出课前准备的三角形，（举起来）你们做的三角形各不相同。选择一种你喜欢的方法快速地验证它的内角和。

探学要求：

（1）做一做：选择你喜欢的方法验证。

（2）议一议：在组内交流你的验证方法和结果。

（3）说一说：用下面的语言格式汇报你再次验证的结果。

（语言表达：我用……方法，验证我做的三角形内角和是……）

生：我用折一折的方法，验证了我做的三角形内角和是180°。

……

师：你们自己做的三角形，大小可能不同，形状也可能不同，但是，通过你们的验证，它们的内角和也都等于180°。

3.了解历史，感悟内化探学方法。

师：在历史上，有许多科学家也都研究过三角形的内角和。例如：法国数学家、物理学家帕斯卡，他在12 岁的时候，就通过自己的研究，发现任意三角形的内角和都是180°。想知道他是怎么研究的吗？

（播放帕斯卡研究过程的录音和课件）

师：帕斯卡也是从特殊想起，通过推想、验证，得出结论的。

4.通过验证，得出结论。

师：现在，我们能得出什么样的结论了？

生：任意三角形的内角和都等于180°。

师：在数学学习中，重要的不是我们知道什么，而是我们是怎么知道的。回顾一下，我们刚才经历了怎样的一个过程，才得到三角形的内角和等于180°这个结论的？

（组内交流，集体分享）

生：我们先在特殊三角形的操作活动中引发猜想——三角形内角和是180°，然后在动手操作中探寻验证猜想的方法，最后得出结论三角形内角和等于180°。

生：我们还经历了自试自探、互助互探、交互群探的自主学习、互助合作的探究学习过程。

三、探学达标

1.计算。

（1）如图8：∠1=75°，∠2=40°，∠3=（ ）。

（2）如图9：∠1=∠2=∠3，求∠3 的度数。

（3）如图10：你知道∠？的度数吗？

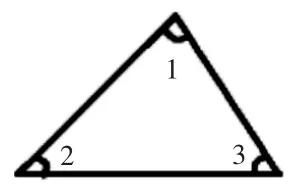
图8

图9

图10

2.操作。

（1）你能画出有两个内角是直角的三角形吗？

（2）你能画出有两个内角是钝角的三角形吗？

（3）你能画出有两个内角是锐角的三角形吗？

探学要求：

（1）画一画：根据要求动手画一画。

（2）说一说：你发现什么？

四、探学总结

1.同学们，今天的这节课，我们一起研究了……通过学习你们都有哪些收获？

2.拓展延伸。

图11