赛塘流域ISVC方法应用中的关键问题分析
2020-06-14臧文斌刘可新
李 匡,刘 舒,臧文斌,刘可新
(1.中国水利水电科学研究院 防洪抗旱减灾工程技术研究中心,北京 100038;2.中国水利水电科学研究院 北京中水科水电科技开发有限公司,北京 100038)
1 研究背景
状态变量初值修正ISVC(Initial State Variable Correction)方法[1]是利用平稳期的预报流量和实测流量建立目标函数,采用优化算法对状态变量初值进行修正,最后利用修正后的状态变量初值重新进行洪水预报。该方法可以应用于历史洪水模拟及实时洪水预报,特别是由于其具有独立性强,适用范围广,不损失预见期等特点,在实时预报中具有一定的应用潜力。在应用时,有以下关键点需要注意,一是平稳期选择;二是平稳期阈值。本文分别对其进行分析讨论。
2 ISVC方法简介
2.1 方法原理典型的洪水预报过程图如图1所示。一场洪水预报过程从计算开始时间到计算结束时间。预报时间一般选在造峰雨结束之后。预报开始时间之前为预热期,预热期内从计算开始时间到流量起涨时间称为平稳期,平稳期内一般只有零星小雨,主造峰雨还未到来,流量也比较平缓,没有明显的上涨过程。

图1 洪水预报过程
水文模型计算时,在平稳期内,由于只有零星降水,预报流量主要来自于状态变量初值,平稳期预报流量的准确性即可反映状态变量初值的准确性。因此可以将平稳期的预报流量与实测流量拟合结果的好坏作为目标函数,采用自动优化算法来修正状态变量初值。由于状态变量初值对洪水预报具有连续性和系统性的影响,平稳期预报准确,整场洪水的预报也更准确。因此,利用修正后的状态变量初值重新进行洪水预报,通常情况下有望显著提高洪水预报精度。基于以上原理,提出基于状态变量初值修正的洪水预报方法,即ISVC方法。
2.2 方法步骤ISVC方法具体计算步骤如下:(1)采用连续模拟至预热期开始时刻的状态变量初值进行洪水预报。或基于经验,人工赋值一套较为合理的状态变量初值进行洪水预报;(2)通过观察预热期内的实测和预报的洪水过程,确定平稳期;(3)计算平稳期内预报流量与实测流量的平均均方根误差NRMSE,判断NRMSE是否大于阈值;如果是,则进行第(4)步,如果不是,则不进行修正,计算结束;(4)计算平稳期的预报流量与实测流量的偏差U;(5)按照U确定初始状态变量修正时对应参数的取值范围;(6)采用粒子群算法寻找最优初始状态变量值;(7)重新进行洪水预报。
2.3 关键点
(1)平稳期选择。平稳期是预热期内计算开始时间到洪水开始起涨的时间,平稳期内主降水还未到来,只有零星降水,预报流量主要受状态变量初值的影响,流量变化平缓。ISVC方法根据平稳期的预报流量和实测流量进行状态变量初值的修正,因此平稳期的选择非常关键。
平稳期采用人工选定方式。人工观察初次预报的预热期内的计算情况,选择实测和预报流量没有明显起涨、主降水开始的时刻作为起涨点,预热期内计算开始时间到起涨点之间为平稳期。
对于历史洪水,平稳期较容易确定;在实时预报时,对于实时洪水,由于河道流量、降水过程是动态变化的,起涨点、主降水开始时刻不易确定,因此,预报员应根据实时流量、降水情况、天气预报以及经验动态滚动确定平稳期。
(2)平稳期阈值。在使用ISVC方法时,不是所有的洪水都需要进行状态变量初值的修正。由于模型输入和模型参数不可避免的出现误差,状态变量初值也会出现误差,但是一定范围内的误差是正常的,因此需要设置平稳期阈值,当初次预报的洪水平稳期误差大于平稳期阈值时,认为该场洪水的状态变量初值误差较大,需要进行修正。当初次预报的洪水平稳期误差小于等于平稳期阈值时,则认为该场洪水的状态变量初值误差合理,不需要进行修正。
在水文预报中,评价预报过程准确度的指标是确定性系数NS,是取值范围小于等于1的数。当NS越接近于1,表明预报流量与实测流量误差越小,当NS=1时,计算值等于实测值。确定性系数适合于有起涨、消退现象过程的评价,对于变化平缓,甚至没有变化的过程,确定性系数的评价并不准确。例如:序列中数据完全相同的两组序列,按照NS的计算公式,分母为0,计算出的NS为无穷大,这显然是不合理的。而平稳期的流量变化平缓,因此用确定性系数计算出的数值不能反映实际情况,归一化误差不受数据序列过程取值的限制,计算出的数值越接近于0,表明误差越小,适合于对平稳期误差的评价。本文平稳期误差采用以下4种归一化误差计算值。
平均相对误差[2](ERE),计算公式如下:

对观测值均值归一化的平均均方根误差[2](ERm),计算公式如下:

对每个观测值归一化的平均均方根误差[2](ERd),计算公式如下:

归一化绝对误差[2](ENAE),将预测的平均绝对误差对观测值的均值归一化,计算公式如下:

式中:QCt为预报流量;QOt为实测流量;QAO为实测流量均值;n为资料序列长度。
当预测无误差时,4种误差的计算结果为0。
ISVC方法目的是对不合格洪水进行修正,以提高预报精度。对于历史洪水,可以通过洪峰误差、洪量误差判断洪水是否合格,而对于实时作业预报时的洪水,由于实测洪峰洪量均不可知,无法计算洪峰误差、洪量误差,无法直接判断是否合格。因此,需要找到平稳期阈值与整场洪水是否合格之间的关系,通过阈值反映洪水是否合格。如果平稳期误差超过阈值,则认为该场洪水不合格,需要修正,反之不修正。
平稳期阈值在编制洪水预报方案时确定。具体的阈值确定方法是,按照预报方案对历史洪水进行模拟预报,统计平稳期误差与合格率。由于洪水预报是连续性的过程,一般情况下,平稳期误差越小,洪水合格的概率越大,平稳期误差越大,洪水合格的概率越小。按照平稳期误差从小到大的顺序排列洪水,分析误差与合格率之间的关系。当平稳期误差大于某一值时,洪水合格率显著降低,这个值就是阈值。
阈值与流域洪水预报方案有关,由于预报方案采用的预报模型、计算时段长、选用的历史洪水等有可能不同,因此不同预报方案,对应的阈值也不相同。阈值确定的核心是历史洪水资料,从统计学的规律来说,更多的样本更能反映统计规律,因此在确定阈值时,需要尽可能多的历史洪水。
在进行实时洪水预报时,阈值是判断是否进行修正的标准。由于流域下垫面条件的变化、水利工程的建设、雨水情测站的调整,以及历史洪水的资料累积,需要及时对预报方案进行调整。此时需要根据预报方案的调整情况,对阈值进行调整。
3 研究对象
3.1 误差评价指标采用ISVC方法对流域洪水进行应用,比较状态变量初值修正前后的的预报成果。用以下3个指标评价修正效果的好坏[3]。
(1)洪峰相对误差

(2)次洪径流深相对误差

(3)确定性系数

式中:QOP、QCP分别为洪峰实测、预报流量;RO、RC分别为次洪实测、预报径流深;QAO为实测流量均值;n为资料序列长度。
图1中柱状图为降水量,实线为实测流量,虚线为初始预报流量,图中竖线左侧为预热期。
3.2 研究模型及其状态变量选择典型的新安江模型[4]进行研究,新安江模型在湿润和半湿润地区有着广泛的应用。在新安江模型中,上层土壤含水量WU、下层土壤含水量WL、深层土壤含水量WD、产流面积比FR、自由水库蓄水量S、壤中流QI、地下径流QG的初值对洪水预报有影响。各状态变量均具有很强的敏感性,对任何一个取值的改变均能对预报结果造成明显的影响。取值范围如表1所示:

表1 新安江模型状态变量取值范围
其中WUM、WLM、WDM、SM为新安江模型的模型参数,通过编制洪水预报方案确定。Q0为计算开始时刻的流域出口流量。
3.3 研究区域及数据赛塘水文站位于赣江二级支流泸水干流,地理位置为东经114°43′40″,北纬27°12′40″,控制流域面积3004 km2。流域多年平均降水量为1553 mm,为典型的湿润地区。赛塘水文站以上流域布设有赛塘、章庄、排头、平都、路口、洋溪、金田等7个雨量站,赛塘流域内无蒸发站,流域附近设有吉安蒸发站。吉安蒸发站所在的牛吼江与泸水均为赣江支流,赛塘水文站与吉安蒸发站直线距离仅20 km,水文气象特性相似。
赛塘流域被划分为4个计算单元,第1单元包含3个雨量站,第2单元包含2个雨量站,第3单元和第4单元均包含1个雨量站。采用泰森多边形法设置雨量站权重。赛塘流域测站分布、计算单元划分见图2。
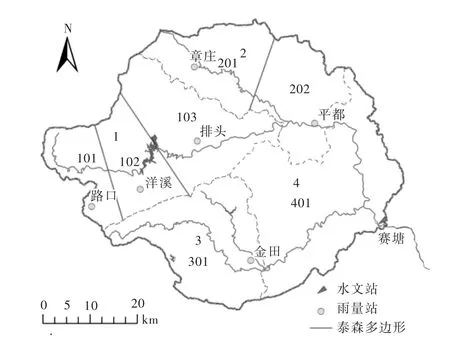
图2 赛塘流域
收集到赛塘流域1992—2018年间的63场洪水资料,包括时段雨量资料、赛塘站流量资料、吉安站日蒸发资料等。采用新安江模型编制预报方案,计算时长为3小时,合格洪水场次为50场,合格率为79.3%,精度评定为乙级。
采用ISVC方法进行修正,平稳期阈值确定为归一化均方根误差NRMSE=58%,共有17场洪水满足修正条件,修正后精度提高的洪水有12场,变好率为70.6%[5]。
4 平稳期选择
4.1 平稳期选择实例赛塘流域洪水主要有两种类型,一种是直接由降水形成的单洪峰洪水过程,另外一种是先有较小降水形成一次较小的洪水过程,然后紧接着由较大降水形成另外一次较大的洪水过程。对于第一种类型洪水,确定其平稳期较为简单,以第14场1997090205号洪水为例说明。该场洪水的开始时间为1997/8/30 8∶00,结束时间为1997/9/5 8∶00,主降水在1997/9/1 2∶00到来,主降水到来之前,实测流量和预报流量均较为平稳,因此选择1997/8/30 8∶00到1997/9/1 2∶00作为平稳期,如图3(a)所示,图中红色竖线为起涨点,红线左侧即为平稳期。对于第二种类型洪水过程,则可以以第一场小的洪水过程作为平稳期,以第11场1995070102号洪水为例,该场洪水开始时间为1995/6/24 8∶00,结束时间为1995/7/3 8∶00,6/25 8∶00-6/29 14∶00出现一次小的洪水过程,洪峰流量523 m3/s,随后在6/29 14∶00-7/3 8∶00出现大的洪水过程,洪峰流量2170 m3/s,两个洪峰相差较大,评价预报精度时以后一个较大的洪峰为评价对象,因此前期的小洪水过程可以作为平稳期,选择6/25 8∶00-6/29 14∶00为该场洪水的平稳期,如图3(b)所示,中间竖线左侧即为平稳期。在实时洪水预报时,对于第二类洪水,往往无法一次准确判断其平稳期,此时可以根据实测及预报降雨、实时河道流量等,结合预报员经验动态调整平稳期。

图3 典型洪水平稳期选择
4.2 平稳期选择影响分析ISVC方法中平稳期应选择主降水还未到来,只有零星降水,流量未发生明显起涨的阶段。如果选择的平稳期中包含了流量发生明显起涨的阶段,将会对修正效果产生明显影响。这是因为起涨的流量主要是由于降水造成的,不能准确反映状态变量初值对流量的影响,会对修正过程造成干扰。
以第7场1994042523号洪水和第23场2000102223号洪水为例进行说明。第7场洪水在4/23 8∶00-4/24 05∶00有少量降水,但是流量还未起涨,4/24 05∶00-4/24 14∶00有较为明显的降水过程,流量也开始起涨,因此设置两个平稳期4/23 8∶00-4/24 05∶00,以及4/23 8∶00-4/24 14∶00;第23场 2000102223号洪水在10/18 8∶00-10/19 08∶00有少量降水,流量未起涨,在10/19 08∶00-10/21 08∶00有明显降水,流量开始起涨,因此设置两个平稳期10/18 8∶00-10/19 08∶00以及10/18 8∶00-10/21 08∶00。对两场洪水在两种平稳期下分别采用ISVC方法对该场洪水进行修正,以判断不同平稳期下ISVC方法的修正效果。
修正结果见表2、图4和图5。表2中第7场洪水修正前的洪峰误差为-43.39%,洪量误差为-43.37%,确定性系数为0.2926;第一种平稳期下的洪峰误差为-14.41%,洪量误差为-4.21%,确定性系数为0.867;第二种平稳期下的洪峰误差为-40.51%,洪量误差为-35.01%,确定性系数为0.4342。第23场洪水修正前的洪峰误差为-40.53%,洪量误差为-35.22%,确定性系数为0.3754;第一种平稳期下的洪峰误差为-19.67%,洪量误差为-0.65%,确定性系数为0.7721;第二种平稳期下的洪峰误差为-29.29%,洪量误差为-18.64%,确定性系数为0.7236。
两场洪水在两种平稳期下的修正结果都比原有结果好,但是第二种平稳期下的修正效果明显不如第一种平稳期。这正是因为第二种平稳期下包含了由于降水产生的流量,使得计算出的平稳期误差没有第一种平稳期下计算的平稳期误差大,导致对状态变量初值的修正幅度没有第一种平稳期下的修正幅度大。平稳期降水产生的流量对状态变量初值的修正造成了干扰,导致修正效果变差。

表2 两场洪水不同平稳期修正结果误差统计
图4和图5为两场洪水两种平稳期下修正结果与修正前结果的对比。

图4 第7场洪水过程修正结果

图5 第23场洪水过程修正结果
以上结果表明,平稳期的选择对ISVC方法的应用有着明显的影响。由于ISVC方法修正的是状态变量初值,平稳期内受其他因素(降水等)影响越小,对状态变量初值修正越有利。因此在选择平稳期时,需要选择实测流量与预报流量均未明显上涨,且主降水开始时刻或者造成平稳期流量上涨的降水结束时刻之前作为平稳期。
5 平稳期阈值影响分析
阈值的设定对ISVC方法的修正效果有着明显的影响。如果阈值设置较小,则认为有较小误差的洪水也需要进行修正,需要修正的洪水场次增多,可能会造成对原有预报效果较好的洪水修正后效果变差的情况;如果阈值设置较大,则认为有较大误差的洪水才需要进行修正,需要修正的洪水场次少,则可能漏掉部分需要修正的洪水场次。
以赛塘流域洪水为例,分别设置三种不同的阈值来分析其对修正效果的影响。设置阈值ERE=30%、ERE=58%和ERE=80%,相应需要修正的洪水场次为40场、17场和5场。修正后的效果如表3所示。
由表3可知,在3种阈值下,需要修正的洪水场次分别为40、17、5次,所需修正的洪水场次逐渐减少,而修正后精度提高的场次分别为23、14、3次,提高率分别为57.5%、70.6%、60%,表明阈值为58%时修正效果最好,而阈值为30%时修正效果最差,阈值为80%时效果次之。这是因为当阈值为30%时,需要修正的洪水场次多,将部分平稳期误差较小,整体预报误差也较小的洪水进行了修正,导致了修正后效果变差,例如第19、27、35、39、45、56号洪水修正前为合格,修正后为不合格;当阈值为80%时,需要修正的洪水场次大大减小,仅有5场,这导致了部分平稳期误差较大,整体误差也较大的洪水不满足修正条件,没有被修正,例如第7、14、23、36、40、48、49、50、57、58场洪水,其初次预报误差较大,均不合格,但是不满足修正条件而没有被修正。赛塘流域平稳期阈值为30%和80%分别对应为过度修正和修正不足。

表3 3种阈值下修正效果统计
平稳期阈值为30%时,参与修正的洪水场次有40场,其中有23场修正后变好,17场修正后变差,特别是第19、27、35、39、45场等5场洪水由修正前的合格变为修正后的不合格,精度下降明显。5场洪水修正前后精度统计如表4所示。5场洪水修整前平稳期的ERE误差在30%~50%之间,修正后虽然平稳期误差变小,但是整场洪水精度变差。
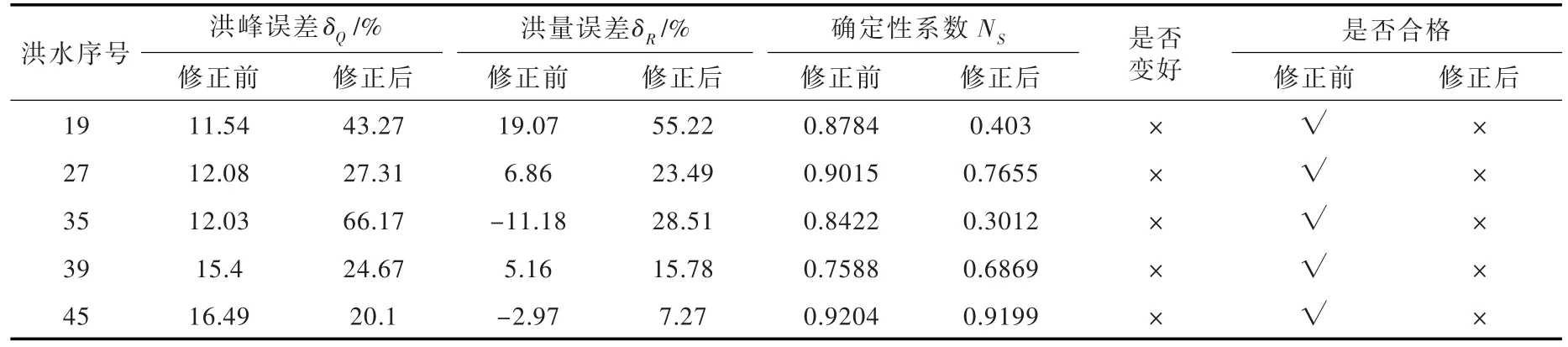
表4 5场洪水修正效果统计
平稳期存在一定误差是正常的,不能过分追求平稳期的预报精度,这样反而会影响到整场洪水的预报精度。在设置平稳期阈值时,应该根据多场历史洪水详细分析,选择合适的平稳期阈值,以避免在修正时出现过度修正和修正不足等情况。
6 结论
本文以赛塘流域为例分析了ISVC方法中的关键点--平稳期以及平稳期阈值,结果表明,二者均对修正结果有着重要影响。
赛塘流域两场洪水不同平稳期下的计算结果表明,平稳期选择对修正结果影响显著,对第7场洪水的洪峰、洪量、确定性系数有明显影响,对第23场洪水的洪峰、洪量有明显影响。同时,第23场洪水是在主降水过程前,还有一次较小降水过程的洪水,修正结果表明,平稳期包含小降水过程形成的洪水过程在内时的修正结果比不包含时更好,因此,对于此类洪水,选择平稳期时,应选择包含小降水过程形成的洪水过程在内作为平稳期。在实时预报中,对于此类洪水应动态选择其平稳期。
平稳期阈值的设置既不能太小也不能太大,阈值设置过小,则需要修正的洪水多,可能存在过度修正的问题;阈值设置过大,则需要修正的洪水少,可能存在修正不足的问题。赛塘流域平稳期阈值分别设置为30%、58%、80%,需要修正的场次分别为40、17、5,修正后精度提高率分别为57.5%、70.6%、60%,分别对应为过度修正、适度修正、修正不足。因此,在确定平稳期阈值时,应尽量选择更多的洪水场次,找出平稳期阈值与整场洪水之间的规律,避免出现过度修正和修正不足的问题。
