基于缓波布置构型的深水立管动力优化机理研究

阮伟东，孙 博，廖小伟

(浙江工业大学 建筑工程学院，浙江 杭州 310023)

钢悬链线立管作为一种较好的油气输送解决方案，在深水油气开发中得到了广泛的应用。但是，随着水深不断增大以及环境愈发恶劣，钢悬链线立管遭受顶端浮体往复运动、无规则水动力荷载和循环土壤抵抗力等作用，可能会产生过大的弯曲应力以及立管顶端和触地区的疲劳损伤破坏。因此巴西国家石油公司研发中心[1-2]针对不同立管布置构型开展极限荷载工况、涡激振动和波致疲劳等研究，发现缓波型立管在结构性能和经济方面是较为合适的深水布置构型。如图1所示，可采用在立管下半段等间距捆绑一定数量浮力块的方法，通过浮力块提供的浮力使立管隆起进而产生缓波波形[3]。该布置可以有效降低立管顶端张力，缓解浮式结构运动对立管触地区的耦合作用，从而提高该区域的疲劳寿命，因此在深海油气开发中得到了越来越广泛的应用。

目前国内外学者对深水环境下缓波型立管动力响应进行了较为广泛的研究。Tanaka等[4]、Pina等[5]、Yang等[6]以及Ai等[7]以最大动应力、疲劳寿命、工程造价以及浮力段参数为优化目标，采用遗传算法、粒子群算法和拟牛顿法等优化算法对缓波型立管进行线型优化设计，获得优化后的浮力块数量、尺寸及其安装位置等参数。此外，孙丽萍等[8]和Sun等[9]研究了深水缓波型柔性立管力学性能在不同布置参数下的变化规律，指出浮力块尺寸和相对位置是高敏感性参数。王金龙等[10]和Wang等[11]结合欧拉·伯努利梁理论和Keller Box有限差分法建立了深水缓波型立管力学分析模型，发现浮式结构运动、管内流体和海流荷载对缓波型立管力学特性具有显著影响。Kim等[12]指出缓波型钢质立管可以有效减缓立管触地区的局部动力屈曲，触地点的应力明显降低，短期疲劳损伤也相对较小。紧接着，王孟义等[13]基于RQ非线性海床土模型建立了缓波型立管三维模型，研究了再贯入阶段土体弱化效应对缓波型立管动力响应的影响。上述研究针对缓波型立管动力响应和疲劳损伤进行了深入的研究，但并未就如何通过构建缓波布置构型实现深水立管动力优化的机理开展更深入的探究。

图1 深水缓波型立管布置构型[3]

通过改进细长杆理论模型，充分考虑管内流体以及海床与立管相互作用等影响因素，基于浮力段等效优化原则引入浮力段参数，建立悬链线、缓波型以及多重缓波型三种立管布置构型的计算模型，将不同布置构型下的立管轴向和法向运动、动态轴力以及曲率响应进行对比研究，为深水缓波型立管的构型设计和结构优化提供一定参考。

1 细长杆理论模型

鉴于深水立管长径比非常大，因此采用立管轴心线描述其构型位置和瞬时形态，基于修正细长杆理论求解立管动力响应特征[14-15]。该理论模型最大优点是其运动控制方程直接建立在整体坐标系下，省去了在不同坐标系间进行坐标变换的繁琐，计算效率得到较大提高，而且包括了全部几何非线性和边界非线性特征。

1.1 模型控制方程

如图2所示，在三维笛卡尔坐标系中，深水立管的构型位置和瞬时形态通过位置矢量r(s,t)进行表达，该矢量是关于立管弧长s和时间t的函数。基于右手螺旋法则，细长杆件轴心线上任意一点正交坐标向量记为(t,n,b)，其中切线方向单位向量t=r′，法线方向单位向量n=r″/|r″|，次法线方向单位向量b=t×n。假定立管横截面与轴心线始终垂直，即不考虑立管横截面发生剪切变形。基于动量守恒以及动量矩守恒原理(图3)建立深水立管运动平衡方程：

(1)

式中：EI为立管抗弯刚度；λ=Tw-EIκ2为拉格朗日乘子，Tw为立管壁厚张力，κ为立管曲率；q为单位长度立管受到的分布式外荷载(其中作用在立管上的水动力荷载包括附加质量力、拖曳力和弗劳德-克利洛夫力)；ρ是立管单位长度质量；上标˙表示对时间求偏导，′表示对弧长求偏导。作用于立管上的附加质量力、拖曳力和弗劳德-克利洛夫力分别采用以下公式进行计算：

(2)

(3)

(4)

其中，ρo和ρi分别为海水密度和内流密度；Ao和Ai为立管外部和内部横截面面积，At=Ao-Ai为立管横截面面积；po和pi分别为静水外压力和静水内压力；Do为立管外径；g为重力加速度；Ca，Cat，Cd和Cdt分别为法向和切向附加质量系数、法向和切向拖曳力系数；af和vf分别为水质点加速度和速度矢量；ey为y方向单元矩阵；T和N为转化矩阵，I为单位矩阵，转化矩阵T和N分别表述为：

T=r′Tr′,N=I-T

(5)

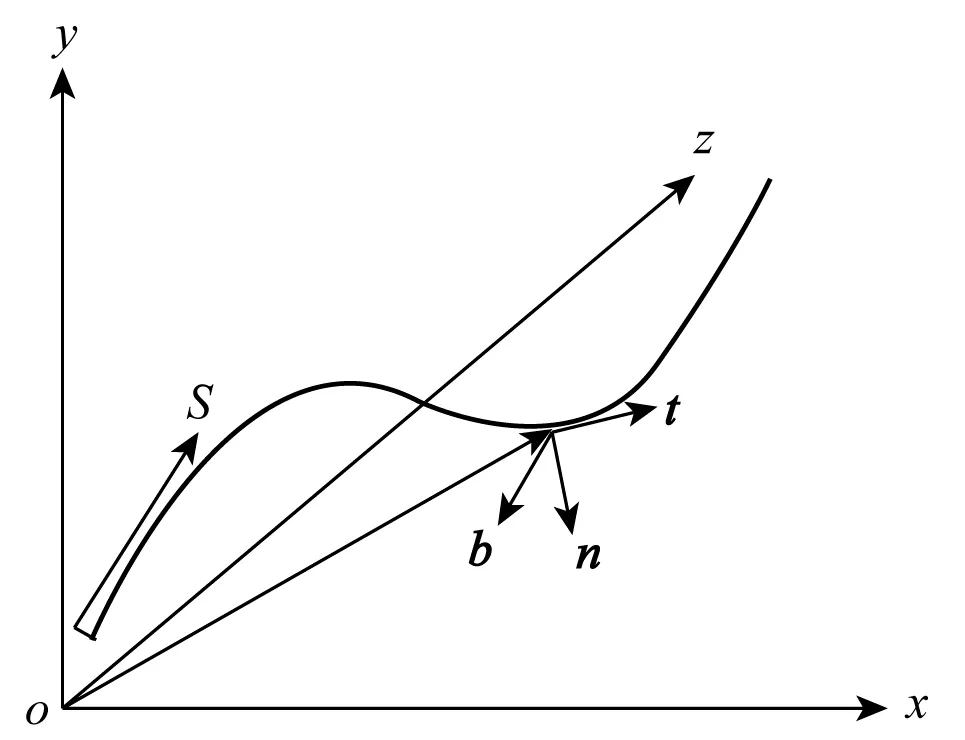
图2 细长杆坐标系示意

图3 细长杆微分单元受力示意

由于立管内部流体流场非常复杂，因此假定立管横截面上流体输送速度相同，从而将管内流体简化为细长体活塞流进行研究[16]：

(6)

其中，u为管内流体流速，该方程右端第一项为内流引起的惯性力，第二项是由立管转动而引起的科氏力，第三项是由于流体要保持与立管的曲率相等而变更其流向所引起的向心力。

最终，细长杆理论模型的运动平衡方程可以修正为：

(7)

其中，

M=(ρtAt+ρiAi)I+ρiAiCaN+ρiAiCatT

(8)

(9)

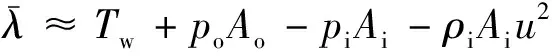
考虑立管静水内外压、管内流体流速以及环向应力引起的轴向变形(该轴向变形与泊松比成正比)等影响，基于小伸缩变形假定推导改进轴向变形约束方程：

(10)

式中：EA为立管轴向刚度；υ为立管泊松比。考虑到立管遭受海水以及管内流体静水压力作用，因此定义不同位置立管受到的静水内外压力。相对于静水外压，还需要考虑立管内部顶端压强，该理论模型将内部顶端压强等效为静水内压高度进行数值计算。此外，该运动控制方程中浮力段外径、单位长度重力以及水动力系数不同于其他立管段参数。

1.2 浮力段等效优化

如图4所示，实际海洋工程中一般将浮力块夹紧于立管中间段上，使其浮力和重力共同作用于悬垂立管上形成环状波形的系统布置，从而有效解耦立管触地区与浮体运动的关系，同时降低立管顶端张力。浮力块一般由具有低吸水性的复合泡沫塑料制作而成，具有较低的流体分离特性。为了避免浮力块滑移致使立管布置形式发生改变，实际工程中需要确保浮力块紧密捆绑于立管上，因此柔性立管铠装层可能会遭受较高的应力。同时进行夹紧作业时要避免夹具损伤立管外套，防止海水渗入管内间隙进而腐蚀立管结构。此外，浮力块经过一定服役周期后会发生浮力损失，因此所设计的立管波型布置要能顺应浮力块浮力损失约10%的情况[17]。

图4 夹紧于立管上浮力块模型[17]

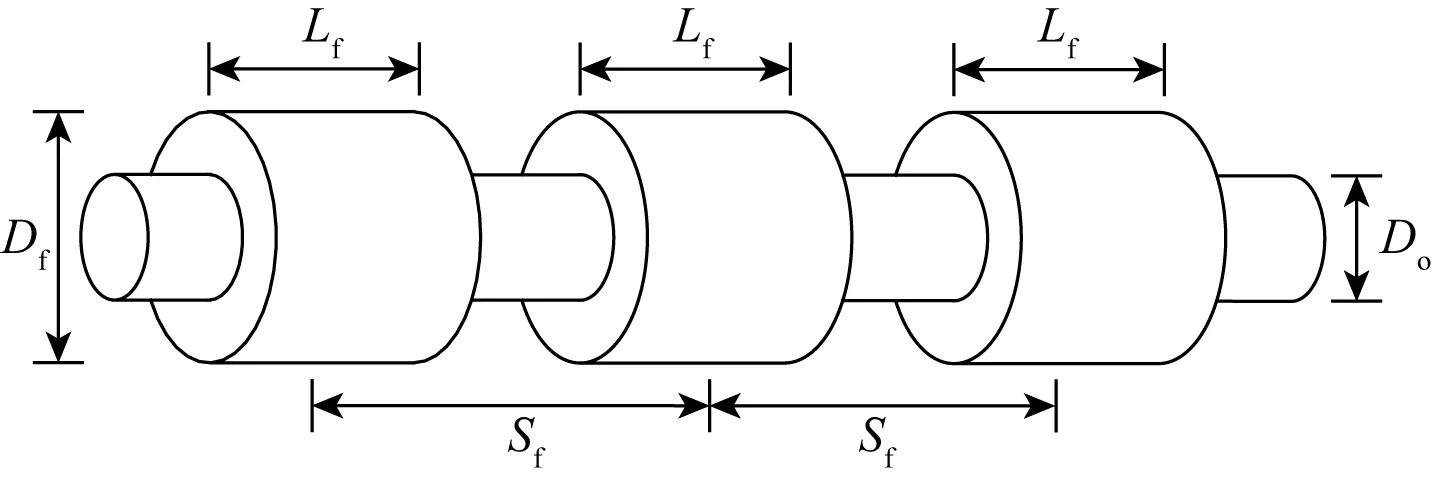
图5 浮力段模型示意

为了便于进行理论分析，对捆绑有浮力块的立管段(简称浮力段，如图5所示)进行等效处理，简化为一段内外径均匀的立管结构。图中Lf为浮力块长度，Df为浮力块外径，Sf为浮力块节距。基于单位长度浮力段水动力荷载以及浮力等效原则，浮力段等效外径De、单位长度等效重力we以及等效水动力系数Cde和Cτe可表达为：

(11)

(12)

(13)

(14)

其中，w为立管单位长度重力，ρf为浮力块材料密度，mfh为浮力块附属索具质量，Cτn为作用于浮力块横截面的切向拖曳力系数。浮力段等效法向和切向附加质量系数可参考拖曳力系数等效过程。

1.3 有限元离散

由于控制方程(7)和(10)呈现较强的非线性特征，因此采用伽辽金法对该偏微分方程进行有限元离散处理，简化为一系列时域计算下非线性常微分方程。为了有效提高微分单元控制方程的计算效率，分别采用埃尔米特三次插值形函数ai(s)和二次插值形函数pm(s)来离散立管形态位置和改进拉格朗日乘子等参数。因此三维笛卡尔坐标系中立管位置矢量、改进拉格朗日乘子、分布荷载、质量矩阵以及轴向应变可以采用张量求和准则近似表达。以位置矢量r为例，其张量求和表达式为：

rn(s,t)=uin(t)ai(s) (n=1, 2, 3;i=1,2, 3, 4)

(15)

(16)

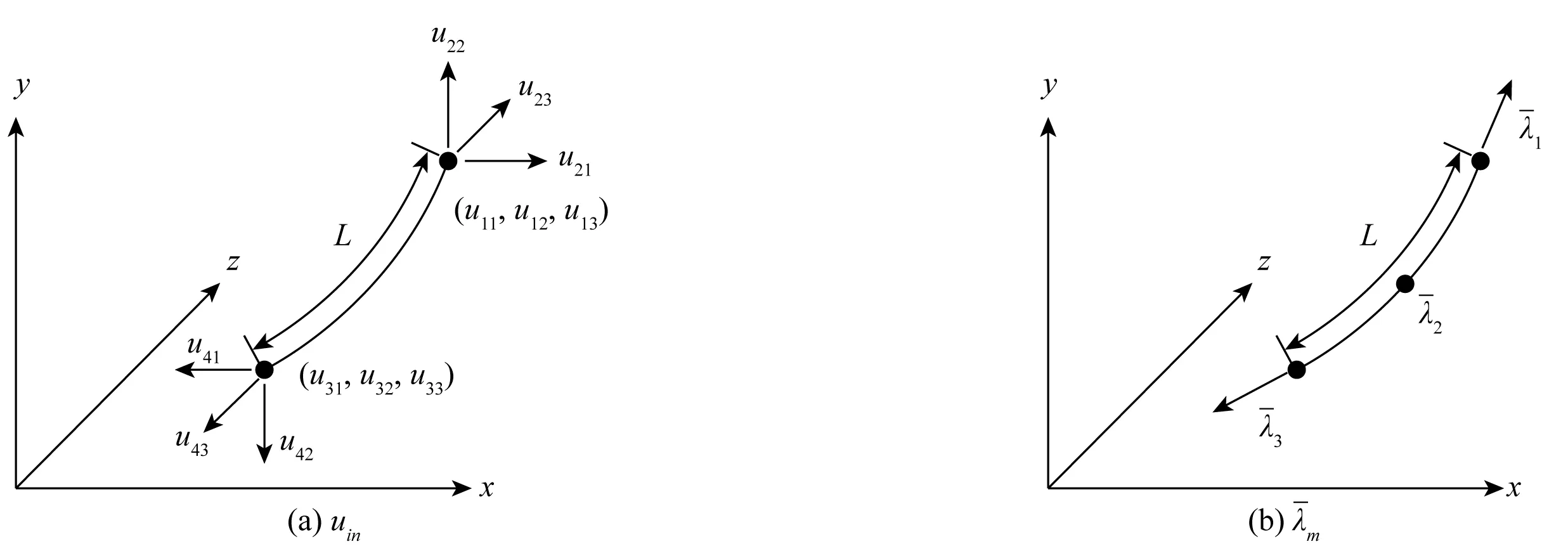
图6 立管微分单元节点变量示意

采用伽辽金法对偏微分方程(7)和(10)分别乘以ai(s)和pm(s)沿着立管单元长度进行积分计算，基于张量求和表达可以推导得到以下常微分方程组：

(17)

(18)

式中：基于张量求和准则的表达式详见参考文献[18]。

1.4 数值计算

2 工程算例

以某水深600 m海域为研究背景，分别建立悬链线立管、缓波型立管以及多重缓波型立管三种深水立管布置构型，采用上述理论模型开展基于缓波布置构型的深水立管动力优化机理研究。柔性立管主要参数见表1，不同构型布置参数见表2。

表1 立管裸管与浮力段主要参数

注：考虑浮力块以及附属索具等参数，对浮力段参数进行等效简化获取相应等效参数。

由于Szczepanski等[19]指出浮体垂荡会加剧缓波型立管垂弯区和拱弯区的应力集中，因此本研究通过在立管顶端施加沿y轴简谐运动，模拟浮式结构垂荡运动。海流剖面图采用幂次法则进行模拟，沿着正x轴方向为海流正向，其幂次法则指数取值为7。此外，根据Aubeny等[20]研究，海床法向刚度取为6.0 kN/m2。

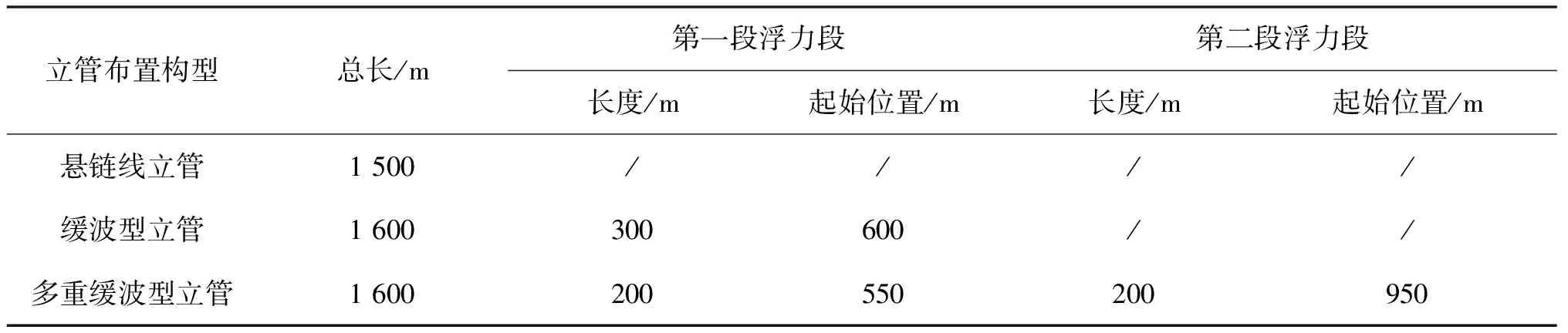
表2 不同立管布置构型参数

注：浮力段和悬垂段编号从悬挂点沿着立管轴心线进行计数，立管划分单元长度为5 m。

3 不同立管布置构型运动响应对比

由于浮式结构运动对海洋立管动力响应的影响较为显著，因此基于上述工程算例，忽略海流对立管运动的干扰，通过在三种布置构型的立管顶端施加不同振幅作用下的简谐垂荡运动(周期为15.2 s，振幅分别为1 m、2 m、3 m和4 m)，研究浮式结构激励运动沿着深水立管的传递过程和运动特征，深入探究缓波布置构型对立管动力响应的影响规律和对触地区运动的解耦机理。图7为基于改进细长杆模型和OrcaFlex有限元模型的多重缓波型立管静态构型、轴力以及曲率对比，而图8为基于改进细长杆模型和OrcaFlex有限元模型的多重缓波型立管动态顶端轴力、末端轴力以及最大曲率对比，从图中可以看出采用改进细长杆模型计算得到的深水立管整体构型、轴力以及曲率等结果与OrcaFlex有限元数值模拟结果非常吻合，充分验证了文中所提出理论模型的可行性和精确性。

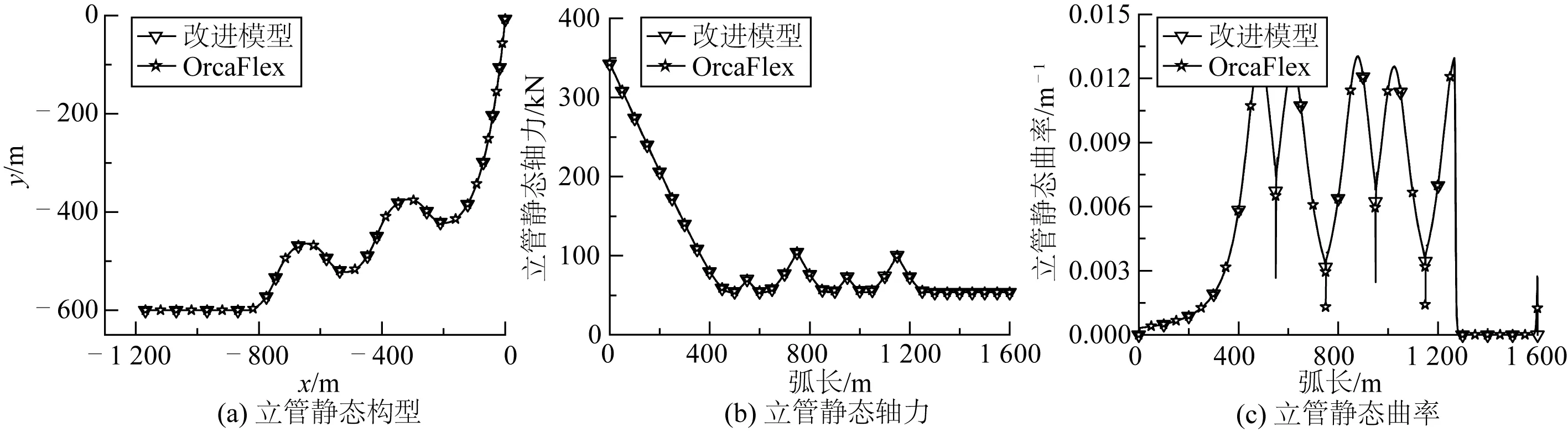
图7 基于改进模型和OrcaFlex模型的多重缓波型立管静态构型、轴力以及曲率对比

图8 基于改进模型和OrcaFlex模型的多重缓波型立管动态顶端轴力、末端轴力以及最大曲率对比

图9至图16为不同垂荡运动作用下悬链线立管、缓波型立管和多重缓波型立管的轴向速度和加速度包络线、法向速度和加速度包络线、最大轴力分布、动态轴力幅值、最大曲率分布以及动态曲率幅值曲线。表3为不同垂荡振幅作用下三种立管动力响应计算结果。

从图9和图10中可以看出悬链线立管、缓波型立管和多重缓波型立管的最大轴向速度和加速度都位于立管顶端。在浮式结构垂荡激振作用下，悬链线立管的轴向速度和加速度包络线沿着立管悬垂段缓慢平滑下降，当传递到触地区时迅速衰减到零，并沿着流线段小幅波动；而缓波型立管和多重缓波型立管通过构建缓波构型致使立管轴向速度和加速度在第一个悬垂段得到大幅衰减。通过对比图11和图12，可以发现这三种立管的最大法向速度和加速度并非发生于立管顶端(即外部激振振源处)，立管法向运动与轴向运动传递规律有显著不同，立管法向速度和加速度并非沿着悬垂段不断衰减下降，而是不断加剧增大(最大值远大于顶端外部激振响应)，其中悬链线立管的最大法向速度和加速度位于立管触地区，而缓波型立管和多重缓波型立管的最大法向速度和加速度则产生于第一个垂弯区，通过缓波构型成功将顶端浮式结构运动和立管触地区运动进行解耦处理。

图9 不同垂荡运动作用下三种立管轴向速度包络线

图10 不同垂荡运动作用下三种立管轴向加速度包络线

图11 不同垂荡运动作用下三种立管法向速度包络线

图12 不同垂荡运动作用下三种立管法向加速度包络线

相同工况下悬链线立管顶端动态轴力和轴力幅值都要显著大于缓波型立管和多重缓波型立管(图13和图14)。由此可见，通过捆绑浮力块构建缓波构型可以有效降低立管顶端动态轴力及其幅值响应。相同垂荡工况作用下，缓波型立管顶端动态轴力及其幅值略大于多重缓波型立管。虽然该工程案例中多重缓波型立管浮力段长度要比缓波型立管浮力段长度增长100 m，但对立管轴力影响并不显著。这是因为立管轴力分布不仅与浮力块长度有关，与浮力段位置也相关。当浮力段整体往立管顶端偏移时，立管顶端轴力将会随之减小。通过对比可以发现，基于缓波布置构型的立管在第一个悬垂段轴力幅值下降非常显著，立管触地区轴力幅值非常小；而悬链线立管的轴力幅值在触地区仍然非常大，仅略小于顶端轴力幅值；当浮式结构运动越来越剧烈，悬链线立管触地区轴力幅值过大可能会产生压缩荷载，进而导致柔性立管发生“鸟笼效应”失效模式。此外，立管触地区的轴力幅值都会出现局部波峰。

图13 不同垂荡运动作用下三种立管最大轴力分布

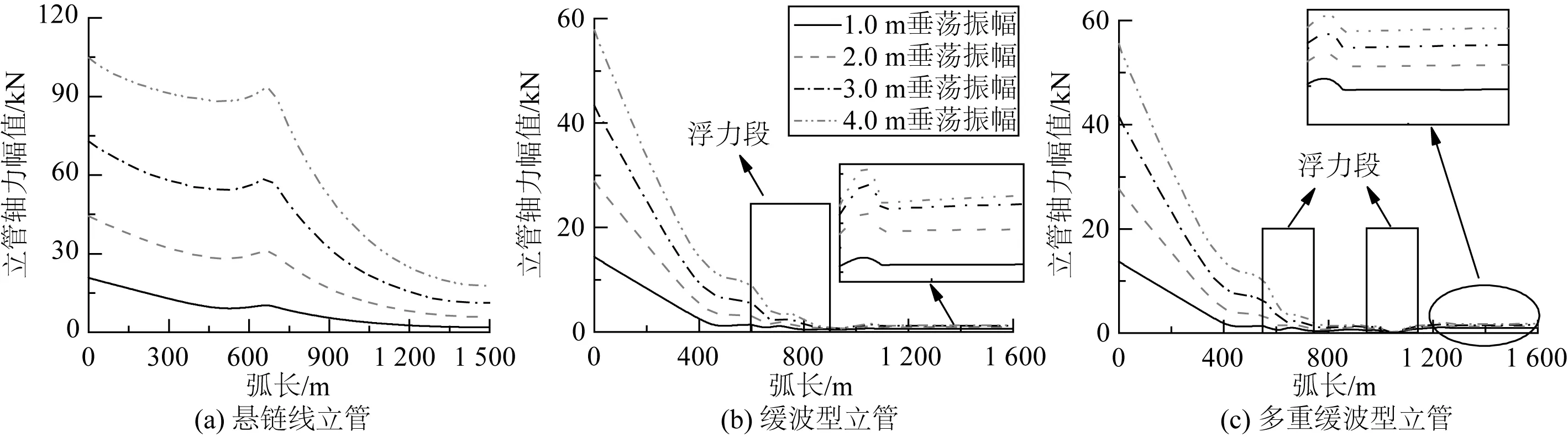
图14 不同垂荡运动作用下三种立管轴力幅值分布

由图15可知，当垂荡振幅为1 m时，悬链线立管触地区的最大动态曲率为0.009 72 m-1，小于相同工况下缓波型立管和多重缓波型立管触地区的最大动态曲率(分别为0.012 43 m-1和0.012 88 m-1)；随着垂荡振幅不断增大，悬链线立管触地区最大动态曲率显著增大，而缓波型立管和多重缓波型立管触地区的最大动态曲率则增大比较缓慢：4 m垂荡振幅作用下三种立管布置构型触地区最大动态曲率分别为0.024 45 m-1、0.012 64 m-1和0.013 03 m-1。这是由于在排除海流对立管力学性能影响的前提下，可以采用悬链线理论对深水立管进行静态分析，其中立管顶端轴力Ttop与局部最大曲率κ的关系为κ=wa/(Ttopsinθtop)。式中：wa为立管表观重力，与立管自重、管内流体重力以及浮力相关；θtop为立管悬挂角。当立管以及浮力块的尺寸和布置确定时，立管顶端轴力Ttop与局部最大曲率κ呈现反比例关系。

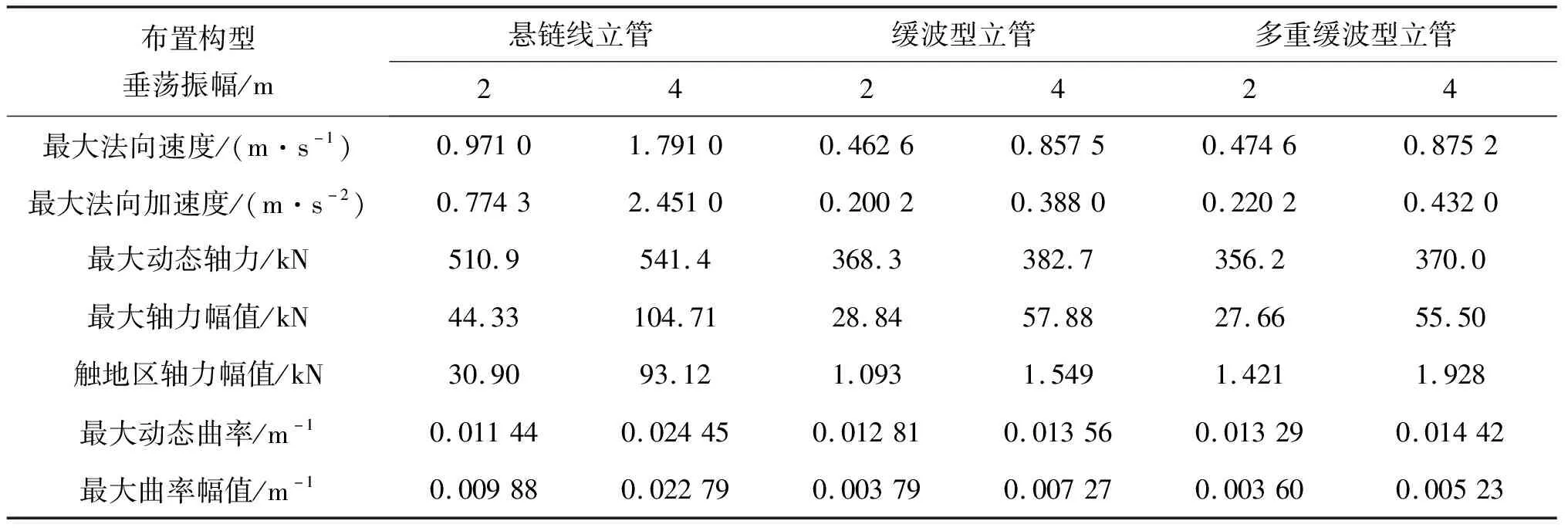
表3 不同垂荡振幅作用下三种立管动力响应

图15 不同垂荡运动作用下三种立管最大曲率分布

因此，在相同立管尺寸和悬挂角工况下，缓波型立管和多重缓波型立管通过浮力段降低顶端轴力，但从另一方面导致了这两种立管布置构型的静态局部最大曲率要大于悬链线立管。当浮式结构运动不显著时，悬链线立管触地区动态曲率也不显著，故而比缓波型立管和多重缓波型立管要小；当浮式结构运动加剧时，缓波布置构型通过有效解耦浮式结构与立管触地区的运动响应，减缓立管触地区的法向运动，进而缓波型立管和多重缓波型立管的动态曲率响应要远远小于悬链线立管。图16为不同垂荡运动作用下三种立管曲率幅值分布。

图16 不同垂荡运动作用下三种立管曲率幅值分布

从图16中可以看出三种立管布置构型的最大曲率幅值都发生在触地区。当浮式结构运动显著时，在降低触地区曲率幅值以及提升疲劳性能方面，多重缓波型立管最优，缓波型立管其次，悬链线立管最后。随着垂荡幅值增大，多重缓波型立管在触地区抗疲劳性能将会越来越明显，当垂荡振幅为5.0 m时，缓波型立管和多重缓波型立管触地区最大曲率幅值分别为0.008 56 m-1和0.006 06 m-1。由此可见，基于缓波布置构型的深水立管可以有效提高触地区的疲劳寿命。

4 海流作用下立管动力响应分析

鉴于立管缓波型布置构型对海流极其敏感，基于三种海流工况(-1.0 m/s，0 m/s和1.0 m/s)研究不同立管布置构型在顶端振幅4.0 m和周期15.2 s的简谐垂荡运动作用下的运动响应，探究海流对基于缓波布置构型的深水立管的影响作用。图17～21为不同海流流速作用下悬链线立管、缓波型立管和多重缓波型立管的布置构型、最大轴力、轴力幅值、最大曲率以及曲率幅值分布曲线。表4为不同海流流速作用下三种立管动力响应计算结果。

图17为不同海流流速作用下三种立管布置构型，从图中可以看出缓波型立管和多重缓波型立管构型对海流比较敏感。当海流从-1 m/s转变为1 m/s，悬链线立管静态触地点x坐标从-258.9 m后退到-290.4 m；而缓波型立管和多重缓波型立管静态触地点x坐标则出乎意料地从-632.2 m前进到-625.5 m和从-843.4 m前进到-835.7 m。此外，通过构建两个缓波波形，可以大大降低立管浮力段波峰与悬垂段波谷的高度差，进而改善管内流体输送环境。

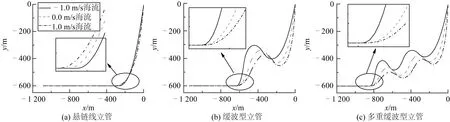
图17 不同海流流速作用下三种立管布置构型

如图18和图19所示，海流对悬链线立管的动态轴力和轴力幅值较为敏感，而对缓波型立管和多重缓波型动态轴力影响呈现多元化。从图中可以看出，三种海流工况下，缓波型立管最大顶端轴力分别为377.3 kN、382.7 kN和393.8 kN；而多重缓波型立管则为365.1 kN、370.0 kN和380.4 kN。可见海流对基于缓波型布置的深水立管顶端区域的动态轴力影响并不大，但对立管触地区和流线段影响却较为显著。

图18 不同海流流速作用下三种立管最大轴力分布

图19 不同海流流速作用下三种立管轴力幅值分布

图20和图21分别为不同海流流速作用下三种立管最大动态曲率和曲率幅值分布，从图中可以看出，海流对悬链线立管触地区动态曲率和曲率幅值影响非常显著，对缓波型立管和多重缓波型立管曲率影响则较为显著。此外，海流对缓波型立管和多重缓波型立管曲率幅值影响最为显著的区域位于第一段悬垂段与浮力段交界处。当海流从-1 m/s转变为1 m/s，悬链线立管触地区最大动态曲率从0.149 10 m-1下降到0.014 48 m-1，降幅高达90%；而缓波型立管和多重缓波型立管触地区最大动态曲率分别从0.036 26 m-1下降到0.007 90 m-1和从0.037 32 m-1下降到0.007 81 m-1。与此同时，悬链线立管触地区曲率幅值从0.148 60 m-1下降到0.013 95 m-1；而缓波型立管和多重缓波型立管触地区曲率幅值在0 m/s海流工况下最大。三种海流工况下多重缓波型立管触地区最大曲率幅值为0.005 23 m-1，而缓波型立管触地区最大曲率幅值则为0.007 27 m-1，比多重缓波型立管高39%。由此可见多重缓波型立管触地区的抗疲劳性能要优于缓波型立管。综上所述，多重缓波型立管相比于缓波型立管在浮式结构和海流共同作用下的动态曲率优化没有显著优势，但在曲率幅值方面却有一定竞争力。

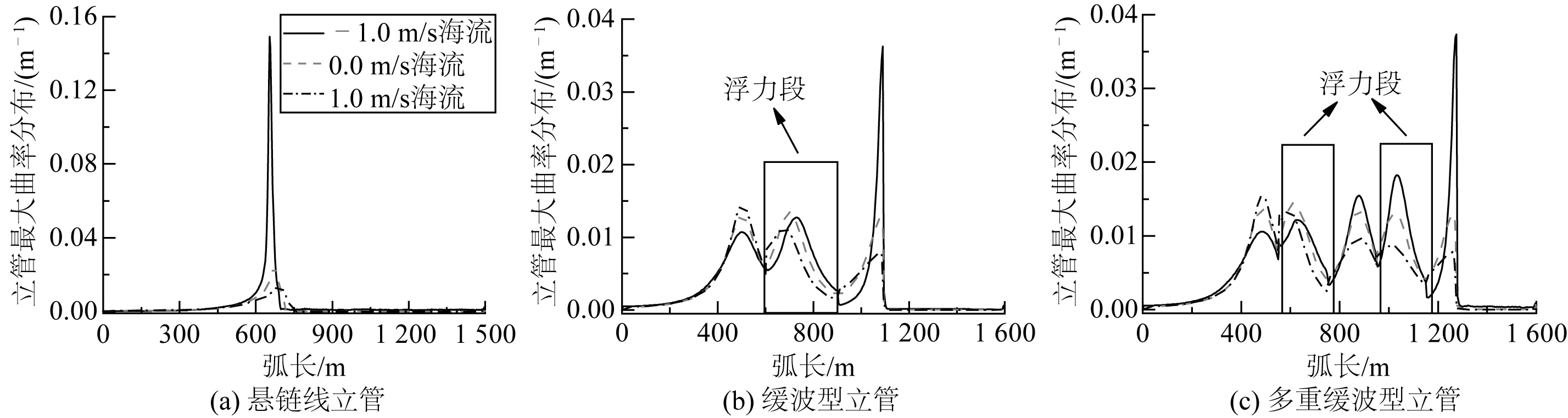
图20 不同海流流速作用下三种立管最大曲率分布

图21 不同海流流速作用下三种立管曲率幅值分布

表4 不同海流流速作用下三种立管动力响应

5 结 语

鉴于缓波型立管能够通过构建缓波构型降低立管顶端张力并解耦浮式结构与立管触地区运动，提出基于多重波形串联布置的深水缓波型立管构型概念，采用改进细长杆理论建立悬链线、缓波型以及多重缓波型三种立管布置构型计算模型，探究基于缓波布置构型的深水立管在浮式结构运动以及海流荷载作用下的响应特征和性能优势，通过对比分析三种立管构型的动力响应和运动传递得出如下结论：

1)基于缓波布置构型的深水立管通过构建缓波构型在第一段悬垂段大幅衰减顶端浮式结构运动响应，有效降低了立管触地区的法向运动响应，极大优化了立管触地区的动态曲率及抗疲劳性能。

2)在不考虑海流影响的前提下，立管局部最大曲率与顶端轴力呈反比例关系。因此，一般情况下，悬链线立管的顶端轴力虽然大于缓波型立管和多重缓波型立管，但是其静态曲率要小于缓波型立管和多重缓波型立管。

3)相比于缓波型立管，多重缓波型立管在动态轴力以及曲率等方面没有显著优势，但在触地区曲率幅值响应上具有一定竞争力。当浮式结构运动剧烈时，多重缓波型立管触地区抗疲劳性能要优于缓波型立管，悬链线立管最差。