不同浸没长度下串列双立管涡激振动数值模拟

武 磊，赵伟文，万德成

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室 船海计算水动力学研究中心(CMHL)，上海 200240)

深海柔性立管因其长细比大，易产生高阶模态涡激振动，进而造成立管结构疲劳损伤乃至破坏，成为海洋工程领域长期以来研究的热点问题之一。区别于刚性圆柱涡激振动，柔性立管在海洋来流的作用下更容易激发出高阶模态的涡激振动，并表现出多模态振动的特性。关于柔性单立管涡激振动问题的试验研究以及数值研究已广泛开展，Wu等[1]对细长柔性单立管涡激振动问题的研究进展进行了总结。随着深海中海洋平台立管数量的逐渐增加，多立管涡激振动问题越发常见。相较于单立管涡激振动情形，立管间的尾流干扰以及立管间距的影响使得多立管涡激振动响应更为复杂。

由于多立管涡激振动研究的开展难度较大，目前关于多立管涡激振动的研究主要集中在双立管情形，且多为试验研究。柔性双立管涡激振动试验研究主要集中在串列、并列以及错列双立管布置形式，主要关注点包括不同立管间距下双立管的涡激振动响应特性[2-6]以及上游立管固定情况下下游立管的振动响应特性[7-8]。Assi[8]通过水槽试验发现，在上游圆柱固定且双圆柱顺流向间距固定为2倍圆柱直径时，在横流向间距小于2倍圆柱直径的工况中，下游圆柱振动表现为典型的流致振动(wake-induced vibration，简称WIV)，在横流向间距为3倍圆柱直径的工况中则表现为明显的涡激振动(vortex-induced vibration,简称VIV)。

目前关于柔性双立管涡激振动的数值研究较为有限。González等[9]通过求解雷诺平均纳维尔-斯托克斯(Reynolds-averaged Navier Stokes，简称RANS)方程和结构动力学控制方程，对Huera Huarte等[7]的试验进行了数值验证计算。计算结果表明，流固耦合计算的数值稳定性受单个时间步内流场与结构场耦合次数的影响较大，而流场网格质量、内迭代次数以及时间步的影响不大。Lin等[10]参考Huera Huarte等[3]的试验，采用离散涡方法(Discrete vortex method，简称DVM)模拟阶梯流中柔性双立管的涡激振动，数值结果与试验结果吻合良好。Chen等[11]采用重叠网格方法对Huera Huarte等[3]的试验工况进行了数值模拟，研究发现立管间距为3倍立管直径时，下游立管表面出现了明显的尾流重附着现象。Wang等[12]通过数值模拟研究了雷诺数为500时立管间距对串列柔性双立管涡激振动响应的影响，研究结果表明当立管间距足够大使得上游立管的尾涡可以从上游立管分离时，上游立管表现为典型的VIV，而下游立管表现为WIV。

从以上分析可知，目前关于柔性双立管涡激振动的试验研究主要关注不同布置形式下立管间距对双立管涡激振动响应的影响，未关注来流剖面沿立管展向分布的影响，而数值研究主要针对模型试验工况进行验证计算且相关研究工作比较有限。

因此，采用viv-FOAM-SJTU求解器，研究阶梯流中立管浸没长度对串列柔性双立管涡激振动响应的影响，求解器的有效性已被Duan等[13]、Fu等[14]和Wu等[15]验证。第一部分介绍采用的数值方法；第二部分介绍数值模拟的计算模型及工况设置；第三部分给出数值结果并进行必要的分析，该部分首先参考Huera Huarte等[3]的试验进行验证计算，然后改变立管浸没长度并给出各工况下的数值计算结果；最后对全文的数值计算结果进行总结。

1 数值方法

1.1 切片理论

图1 切片模型

考虑到深海柔性立管的轴向尺度较大，若对其涡激振动进行全三维数值模拟将消耗大量计算资源，因此采用切片理论对流场进行简化。切片理论即使用二维流场切片沿立管展向进行均匀划分，并认为将切片所受水动力进行插值可得到模型整体受力，切片理论的有效性已被Herfjord等[16]证明。如图1所示为立管的切片模型。

1.2 流场控制方程

针对每个切片，通过求解不可压缩RANS方程得到切片所受的流体力。RANS方程表述如下：

(1)

(2)

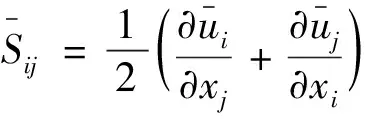
1.3 结构动力学控制方程

结构动力学计算部分，将立管视为两端简支的小位移欧拉-伯努利弯曲梁模型，忽略顶张力随时间的变化。来流中均质立管在顺流向及横流向的受力平衡方程可表示为式(3)、(4)。

(3)

(4)

式中：EI为立管弯曲刚度；T(z)=T-ωs(L-z)为立管轴向张力，其中T为立管顶张力，ωs为立管在水中的单位长度重力，已考虑浮力影响，L为立管长度；m、c、k分别为单位长度立管的质量、阻尼以及刚度。

考虑到立管两端边界条件为简支，即位移和弯矩为0，通过有限元方法将式(3)、(4)离散，可得到立管的结构运动控制方程，即式(5)、(6)中的二阶常微分方程，详细推导过程可参考文献[17]，其求解采用纽马克-贝塔(Newmark-β)[18]法。

(5)

(6)

式中：M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵；x、y分别为立管结构顺流向和横流向的位移响应，变量上方的圆点代表对时间的导数；Fx、Fy分别为立管顺流向和横流向所受的水动力载荷。阻尼矩阵C基于瑞利阻尼模型获取，表述如下：

C=αM+βK

(7)

图2 流固耦合求解流程

(8)

流场部分和结构动力学部分的耦合计算通过流固耦合模块完成，如图2所示。在每个时间步内，首先将流场计算模块求解得到的各切片所受流体力，插值映射到各结构节点上；然后，依此计算结构位移响应；进而将结构节点位移映射到流场，以完成流场网格的更新；最后完成时间步的向前推进。其中，流场网格的变形操作采用OpenFOAM自带的Laplace方法完成。

2 问题描述

文中的数值计算模型参考Huera Huarte等[3]开展的阶梯流中串列双立管涡激振动系列试验。由于模型试验只关注下游立管的振动响应，只在下游立管上安装测量仪器，因此双立管的结构参数略有不同，详细参数如表1所示(上标a代表上游立管)。

模型试验中，双立管串列布置，立管间距为3D。双立管处于阶梯流中，即立管下部40%长度处于均匀流中，流速为0.55 m/s，立管上部60%长度处于空气中。本文的数值模拟中，首先对试验工况进行验证计算；然后将流速设为0.3 m/s，并改变立管浸没长度，计算浸没长度在40%～70%(间隔15%)立管长度下的双立管振动响应。

表1 立管模型的主要结构参数

由于立管上部处于空气中的部分长度所受的升阻力较小，参考Chen等[11]研究忽略立管处于空气中部分长度所受的升阻力载荷。因此双立管处于空气中的长度部分不设置切片，网格总量得以减小。图3为阶梯流中串列双立管的切片布置示意，切片沿立管轴向均匀布置，其数量随立管浸没长度改变。所有切片的计算域以及网格划分一致，如图4所示，网格y+值约为3。流体沿x正向流动，流动入口距上游立管15D，流动出口距下游立管30D，上下边界分别距立管中心15D。靠近立管中心区域的网格划分较密，靠近计算域边界的网格较为稀疏。流体控制方程的边界条件设置为：流动入口的速度边界条件与来流一致，流动出口设置为相对值为0的压力出口，双立管表面设置为无滑移边界，垂直于切片上下侧面以及立管展向边界方向的速度设为0。

结构动力学计算部分，将立管模型均匀划为80个结构单元，总共81个结构节点。其中，处于均匀流场中的结构单元数随浸没长度均匀变化。

图3 串列双立管的切片布置

图4 切片网格划分

3 计算结果及分析

3.1 试验工况验证计算

为确保数值计算结果的有效性，首先参考试验工况开展了验证计算。验证计算工况选取立管间距S=3D，顶张力T=110 N，流速U=0.55 m/s。针对试验工况的验证计算共选取3套网格，网格1、网格2以及网格3中单个切片的网格量分别为26 000、45 000以及80 000。图5给出了3套网格中的上下游立管横流向以及顺流向的振动位移均方根曲线，可以看出网格2与网格3的计算结果基本吻合，而网格1由于过分稀疏，计算结果稍差。整体而言，求解器的网格收敛性良好，因此文中选取网格2作为计算网格。

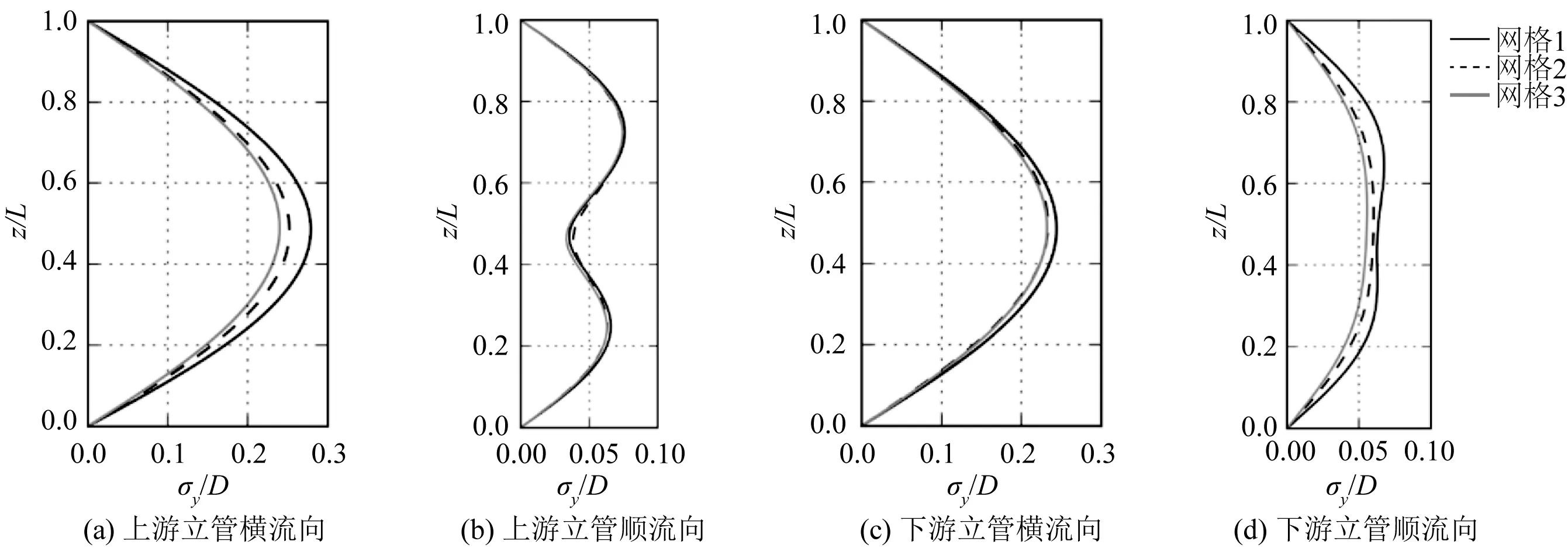
图5 立管横流向及顺流向位移均方根

图6为下游立管中间节点的横流向振动位移时历曲线，可以看出中间节点的横流向振幅最大值可达0.8D。图7给出了下游立管的瞬时振动轮廓叠加图。其中图7(a)、7(b)、7(c)分别表示模型试验中下游立管相对平衡位置的横流向振动轮廓、顺流向振动轮廓以及相对于平衡位置的顺流向振动轮廓；图7(d)、7(e)、7(f)分别是与试验结果相对应的数值模拟结果。

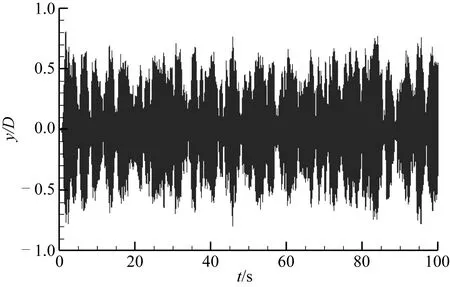
图6 下游立管中间节点横流向振动时历曲线

图7 下游立管的瞬时振动轮廓叠加图((a)、(b)、(c)为试验结果，(d)、(e)、(f)为数值结果)

可以看出，下游立管横流向及顺流向的主振模态均为一阶，数值计算结果与模型试验结果基本一致。模型试验中，下游立管横流向振幅范围为-0.75D～0.68D，顺流向振幅范围为-0.03D～0.18D；与试验结果相对应的数值模拟结果分别为，横流向振幅范围-0.74D～0.68D，顺流向振幅范围-0.04D～0.17D，数值误差在可接受范围内。

图8给出了下游立管中间节点的位移功率谱密度(Power spectral density，简称PSD)，其中图8(a)、8(b)分别为模型试验中横流向及顺流向的位移功率谱密度，图8(c)、8(d)分别为与试验结果相对应的数值结果。可以看出，模型试验中，下游立管的横流向振动为单一频率的一阶振动模态，频率约为6 Hz；顺流向振动的主振模态仍为一阶，主振频率约为6 Hz，同时存在较为微弱的二阶模态成分，频率约为12.5 Hz，可以看出，下游立管顺流向表现出了多模态振动特性。数值模拟中，下游立管的横流向振动响应与试验结果一致，为单一频率的一阶振动模态，主振频率为6 Hz；顺流向主振频率仍为6 Hz，并且位移功率谱中同样发现了较微弱的二阶模态成分，而频率约为14 Hz，与试验结果有一定的误差。引起顺流向二阶振动频率误差的原因可能是，数值模拟中采用二维切片模拟流场，忽略了尾涡的三维效应，并且在将水动力载荷映射到结构单元时对每个切片所代表的立管长度范围采用均匀插值，难以精确模拟实际水动力载荷的分布，因此造成数值计算所得的振动频率与试验结果存在误差。但总体而言，数值模拟结果与试验结果基本一致，求解器的有效性较为可信。

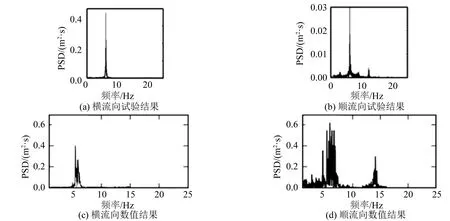
图8 下游立管中间节点的位移功率谱密度

3.2 浸没长度对立管涡激振动的影响

基于对试验工况进行的验证计算，文中进一步研究了浸没长度对立管涡激振动的影响。选取的计算工况是来流速度为0.3 m/s，串列双立管的浸没长度分别为0.40L、0.55L、0.70L，分别记为工况1、工况2、工况3，其余的计算设置与3.1节中的验证计算工况一致。本节将分别介绍不同浸没长度下上游立管及下游立管的涡激振动响应特性。

3.2.1 上游立管振动响应

图9(a)和图9(b)分别给出了上游立管横流向及顺流向沿立管展向的无量纲化位移均方根。可以看出上游立管的横流向振动在各工况下均为一阶，而顺流向振动仅在工况1中为一阶，在工况2和工况3中主振模态增大为二阶。随着浸没长度的增加，立管整体所受的水动力载荷有所增大。由于数据取样时间的差异，尽管工况2和工况3的最大位移均方根基本相同，但立管横流向的位移均方根整体上呈现出增大的趋势。图9(b)展示的顺流向位移均方根结果则有所不同。在工况1中，立管顺流向主振模态为一阶，频率较低，立管的顺流向振动得以充分发展，其最大位移均方根大于后两种工况；而在工况2和工况3中，立管顺流向的主振模态变为二阶，振动频率较高，立管的顺流向周期性振动来不及充分发展便已进入下一周期，因此最大位移均方根较工况1有明显的减小。

图9 上游立管无量纲化位移均方根

上游立管横流向和顺流向的展向位移功率谱密度分别在图10和图11中给出。图10为3种工况中上游立管横流向位移功率谱密度。可以看出，3种工况中上游立管的横流向主振模态均为一阶，主振频率分别为3.3 Hz、3.2 Hz、3.1 Hz，且工况3的振动频率包含较微弱的一阶高频率成分。图11为3种工况中上游立管顺流向位移功率谱密度。工况1是频率为6.7 Hz的纯一阶振动模态，工况2、工况3则是主振频率为8.6 Hz的二阶振动模态。随着浸没长度的增加，立管整体承受的水动力载荷增加，更容易激发出高阶振动模态。高频率的振动会直接影响立管的振动位移能否得到充分发展，这解释了图9(b)中3种工况中立管的顺流向最大位移均方根的差异。

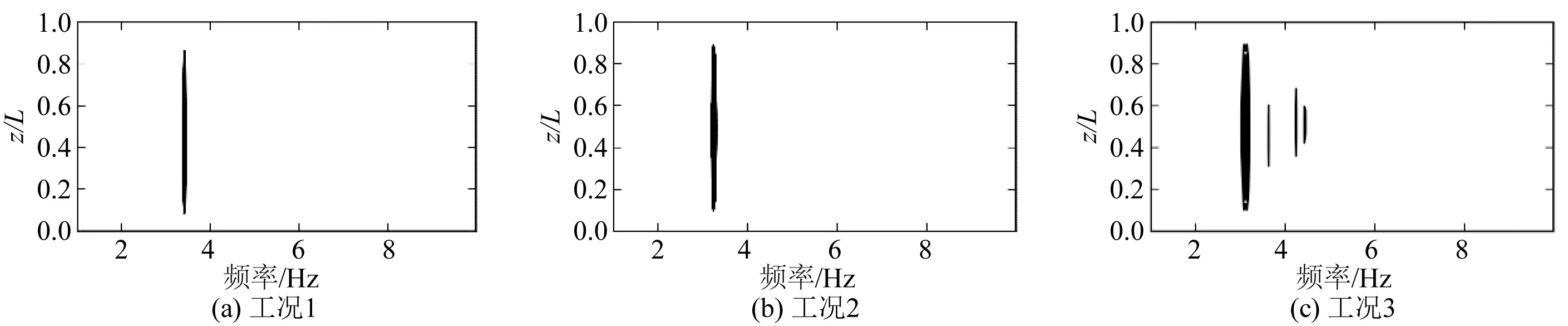
图10 上游立管横流向的展向位移功率谱密度

图11 上游立管顺流向的展向位移功率谱密度

3.2.2 下游立管振动响应

图12(a)和图12(b)分别给出了下游立管横流向及顺流向的无量纲化位移均方根沿立管展向的分布。从图12(a)可以看出，三种工况中下游立管的横流向主振模态均为一阶，且由于工况2和工况3中下游立管整体承受的水动力载荷增加，立管的最大位移均方根均达到了0.15D，约为工况1的两倍；关于顺流向的振动响应结果，工况1中下游立管仍表现出一阶振动，而工况2和工况3则均呈现出二阶主振模态。与上游立管顺流向的位移响应类似，工况2和工况3的顺流向最大位移均方根均小于工况1，仅为0.025D，约为工况1的三分之一。这是由于工况2和工况3中下游立管的主振频率较高，其顺流向的周期性振动来不及充分发展便已进入下一周期。

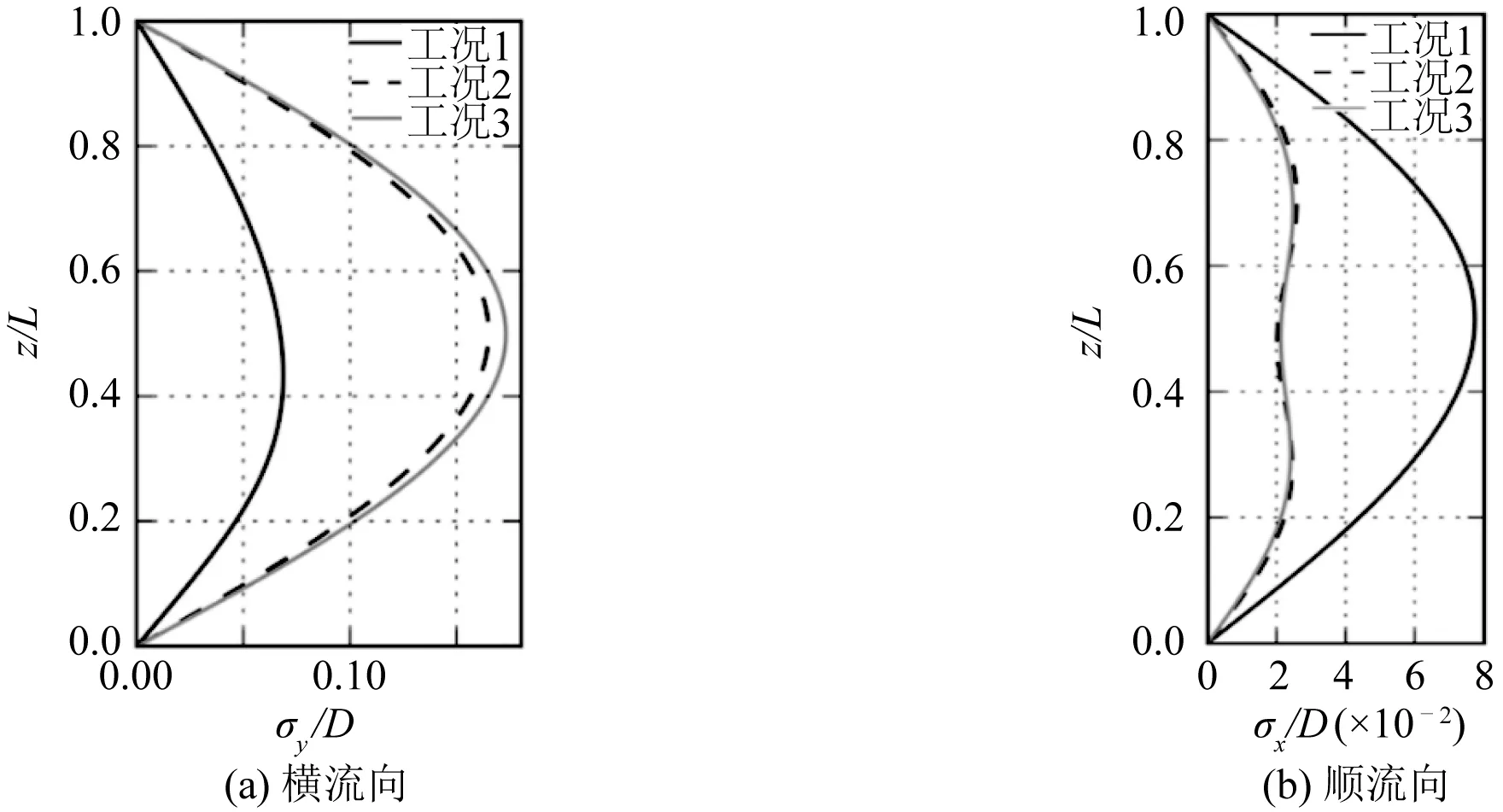
图12 下游立管无量纲化位移均方根

综合比较图9和图12可以发现，3种工况中上下游立管在横流向及顺流向的主振模态均保持一致。这可能是由于计算工况中流速设置的较小，对应的雷诺数仅为4 800，上下游立管的泻涡差异未得到充分激发。同时，由于上下游立管的间距较小，下游立管同时经受远方来流及上游立管尾流的作用，在3种工况中，下游立管的横流向及顺流向的位移均方根均大于上游立管。

图13和图14分别给出了下游立管横流向及顺流向的展向位移功率谱密度。3种工况中下游立管的横流向主振模态均为一阶，主振频率分别为3.4 Hz、3.2 Hz、3.1 Hz。从图14可以看出，工况1中下游立管顺流向表现为频率为6.8 Hz的单一频率一阶振动模态，工况2和工况3中下游立管顺流向则体现出了多模态振动特性。工况2和工况3的主振模态均为二阶，且伴随有较高比重的一阶频率成分。工况3中各阶模态的频率范围较工况2更广，这是由于立管浸没长度的增加使得立管承受的水动力载荷增加，且下游立管受到上游立管尾流的影响更大。

综合分析图10、图11、图13以及图14，随着浸没长度的增加，上下游立管受到的水动力载荷增加，立管顺流向的主振模态也会增大。同时，下游立管受到上游立管尾流的影响，下游立管在顺流向的振动更容易表现出多模态振动特性。

图13 下游立管横流向的展向位移功率谱密度

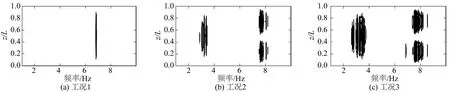
图14 下游立管顺流向的展向位移功率谱密度

为进一步说明下游立管顺流向振动的多模态特性，图15和图16分别给出了工况2和工况3中下游立管在不同时段的顺流向位移时空云图，图中实线等值线代表正值，虚线等值线代表负值。图15(a)中下游立管表现为纯二阶振动，图15(b)中则表现为纯一阶振动，而在图15(c)中则同时出现了二阶振动与一阶振动。可以看出，工况2中下游立管的顺流向振动表现出明显的多模态振动特性，随着时间的推移，立管的主振模态在二阶与一阶间切换。在图16给出的工况3中下游立管的顺流向位移时空云图中，同样观察到了多模态振动的特性。图15和图16给出的下游立管顺流向振动的多模态特性与图14(b)、图14(c)的结果一致。工况2和工况3中下游立管顺流向的多模态振动特性可以解释为，浸没长度的增加导致上游立管的尾流对下游立管的泻涡影响较大，使得下游立管泻涡频率不稳定，进而造成了下游立管顺流向的多模态振动。

4 结 语

基于深海立管流固耦合求解器viv-FOAM-SJTU，对阶梯流中串列双立管涡激振动开展数值模拟。首先针对试验工况开展验证计算，数值结果与试验结果吻合良好，验证了求解器的有效性。为研究不同浸没长度下串列双立管的涡激振动响应，选取了浸没长度分别为0.40L、0.55L和0.70L的3种工况展开计算，计算模型与模型试验保持一致，流速设置为0.3 m/s。通过对3种工况中上下游立管的位移响应及频率响应进行分析，得出了以下结论：

1)随着浸没长度的增加，立管整体承受的水动力载荷增加，上下游立管的顺流向主振模态均从工况1中的一阶转变为工况2和工况3中的二阶。

2)在横流向振动均为一阶的情况下，由于工况2和工况3中立管承受的水动力载荷较大，上下游立管的横流向位移均方根值均大于工况1；关于顺流向振动，由于工况2和工况3中立管的主振模态均为二阶，立管的周期性振动来不及充分发展便进入下一振动周期，因此工况2和工况3中上下游立管的顺流向位移均方根值均小于工况1。

3)随浸没长度的增加，下游立管的泻涡受上游立管的尾流作用加强，泻涡频率变得不稳定，使得工况2和工况3中下游立管的顺流向振动表现出了明显的多模态振动特性。