基于格子Boltzmann方法的斜坡堤越浪数值模拟研究
2020-06-14李薪丰张庆河张金凤刘光威
李薪丰,张庆河,张金凤,刘光威, 2
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300350; 2.清华大学 水沙科学与水利水电工程国家重点实验室,北京 100084)
斜坡式海堤是海防工程中常见的结构物,海堤发生破坏可能给人们的财产与生命安全带来重大损失。越浪往往是造成海堤破坏的重要因素,因此海堤越浪研究具有重要意义。早期的越浪研究主要集中在物理模型试验,随着波浪理论和计算机技术的发展,越来越多的数值方法,如基于N-S方程的OpenFOAM、Fluent、Flow-3D等开源或商业软件[1-3],以及基于拉格朗日方法的光滑粒子流体动力学(SPH)模型[4-5],被应用于越浪过程的研究。
近年来,格子Boltzmann方法(lattice Boltzmann method,简称LBM)作为新型的流体数值模拟方法,凭借其算法简单,计算效率高,并行计算可扩展性好,能方便处理复杂边界条件等优势,在涉及流体模拟的很多领域得到了广泛应用[6],但目前应用LBM对波浪问题进行模拟的工作还只见于少量文献[7-10]。Liu等[11]指出,LBM方法在波浪研究中未能得到广泛应用的原因在于,已有文献在利用LBM模拟波浪时存在较为严重的波浪衰减问题。Liu等[12]进一步分析了波浪衰减原因,并提出了压力修正格式,解决了波浪衰减问题,为LBM应用于波浪模拟奠定了基础。
为进一步验证修正格式LBM模拟波浪和结构物相互作用的能力,将采用刘光威[13]建立的二维数值波浪水槽,对光滑斜坡堤上规则波与不规则波越浪进行模拟,并将计算结果与已有试验数据以及其他数值模型的模拟结果进行比较。
1 数值模型
对于斜坡堤越浪问题,参考坐标系如图1所示,坐标原点O固定在入口与底面相交处,x轴正方向为波浪的传播方向,y轴正方向为结构物的高度方向,SWL表示海边界静水位。
图1 斜坡堤越浪问题的参考坐标系
1.1 LBM方法
在LBM模型中,流体抽象为大量的粒子,这些粒子在简单的网格上进行碰撞和迁移,根据反映粒子分布状态的分布函数和宏观物理量之间的关系即可获得密度和速度等宏观流动信息。LBM只描述粒子的统计行为,而不关心粒子的个体行为,也可以看做是Boltzmann方程的特殊离散形式。
传统的LBM在模拟波浪时,采用单相流模型,只对水相进行模拟,通过自由表面边界条件来表示气相对水相的影响,为考虑外力项(如重力)需要在LBM模型中添加作用力项,正是由于自由表面边界条件与作用力项的耦合误差,造成非物理流动引发了波能衰减与数值振荡。为消除耦合误差,Liu等[12]将重力引入压力梯度项,采用如下不带作用力项的多松弛(MRT)模型的控制方程:
(1)
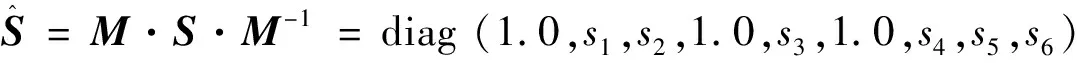
(2)
式中:ωα为各个离散速度方向的权系数,在D2Q9模型中,ω0为4/9,ω1~ω4为1/9,ω5~ω8为1/36。其对应的离散速度如下:
(3)
通过下式可以从分布函数中得到与流体运动有关的宏观信息,用于计算碰撞步中的平衡态分布函数:
(4)
Liu等[12]采用修正压强格式后,将重力引入压力梯度并将其从LB方程右侧的作用力项中移除,当模型中外力项只包含重力时,方程中就不存在作用力项,进而避免了由于自由表面边界条件与作用力项耦合而带来的误差。

1.2 边界条件
模型采用主动吸收式速度入口造波方法[13]。速度入口造波方法只需要给出计算边界处水质点运动速度以及水位。首先根据正确的波浪理论计算出造波边界处的理论水位ηT以及水质点的理论运动速度uT。然后根据理论水位ηT判断造波边界处各个格点的体积分数φ:
(5)
式中:yc为格点的垂向坐标,h为静水位,r为缓启动系数,其表达式如式(6)所示:
(6)
式中:Tramp是设置的缓启动时间。根据理论水位、水质点理论运动速度以及格点垂向坐标计算边界格点的速度:
uc=(φ×r)uT(yu,t)
(7)
式中:yu为计算格点流速时的垂向坐标,当格点位于理论水位下方时,使用格点垂向坐标yc计算流速;当格点位于理论水位上方时,使用静水位h计算流速。
模型采用出流边界消波方法[13],边界处采用带垂向分布的出流流速:
(8)

(9)
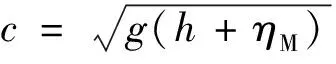
将出流边界消波方法应用于速度入口边界条件,则可以实现吸收反射波的效果,此时ηR=ηT-ηM。主动吸收速度入口造波边界上格点的水平流速为:
(10)
由于LB方法在计算过程中只求解密度分布函数,实际应用中往往将边界上的速度或压强等宏观量作为已知条件,因此采用非平衡态外推数值格式来实现边界上由宏观量重构密度分布函数的过程[12-13]。
1.3 自由表面模型
界面追踪模型采用Thuerey[14]提出的基于VOF方法的单相自由表面LB模型[12-13]。根据离散单元的体积分数φ追踪自由表面,即按照体积分数来定义气相、界面和液相格点:

(11)
式中:b为单元的孔隙率,体积分数φ定义如下:
(12)
其中,Al(x,t)为x格点所在单元体内流体的面积,Ac为单元的面积,m(x,t)为单元体内液相流体质量。该模型从分布函数的物理意义出发,由格点x迁移至相邻格点的分布函数可被视为从格点流出的质量,而由相邻格点迁移至格点x的分布函数被视为流入格点单元的质量。则从t时刻到t+1时刻格点α方向的质量变化Δmα为:
(13)

(14)
则t+1时刻的格点单元液相流体质量为:
(15)
有了新时刻的质量之后,通过式(12)计算所有界面格点新时刻的体积分数,然后根据式(11)更新界面格点新时刻的状态。
2 光滑斜坡堤上越浪的LBM模拟
2.1 光滑斜坡堤上规则波的越浪模拟
Saville[15]对坡度为1∶3和1∶1.5的光滑斜坡堤上规则波越浪进行了大量的试验研究。Soliman[16]和闫科谛[1]分别利用基于求解RANS方程和VOF方法的二维破波数值模型(BWNM)、三维OpenFOAM模型对越浪过程进行了详细的数模研究,并与Saville[15]的试验数据进行了比较。Shao等[4]和Ni等[5]分别利用基于SPH方法的二维ISPH模型、二维DualSPHysics模型也进行了类似的数值试验。这里采用基于LBM建立的二维数值波浪水槽对规则波作用下光滑不透水斜坡堤越浪进行模拟,并将计算结果与Saville[15]试验值以及其他模型的模拟值进行比较。采用无量纲平均越浪量Q作为比较参数,其定义如式(16)所示:
(16)
其中,H0是深水波高;g为重力加速度;q为平均越浪量,m3/(m·s)。q的计算方法为:模拟过程中实时输出越过斜坡堤堤顶竖直面的流体体积通量φ,即为每个时间步的堤顶瞬时越浪量q(t),对q(t)进行积分运算,再除以积分段时间间隔,即可得到平均越浪量q。
试验海堤剖面如图2所示,海堤设置在坡度为1∶10的缓坡上,其中dt、ds、Rc分别表示海边界静水位(SWL)以下水深、结构趾部SWL以下水深、SWL以上结构顶面(干舷)高度。文中选取海堤坡度为1∶3的16组算例进行了模拟,16个算例的深水波高均为1.0 m。按照原型比尺进行模拟,详细的试验参数和计算结果如表1所示,其中Ht为造波边界处的波高值,T为周期。
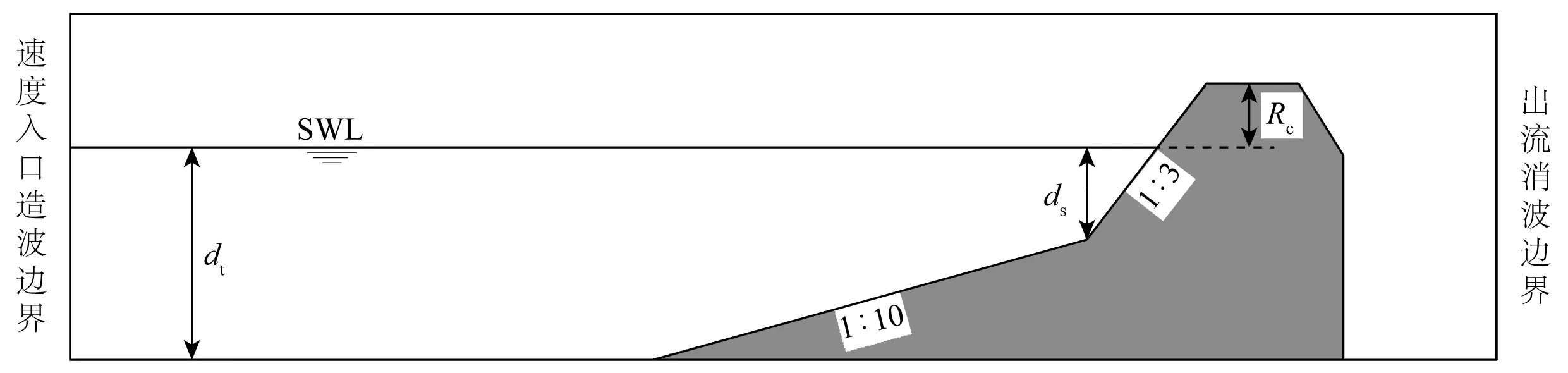
图2 规则波作用下斜坡堤断面
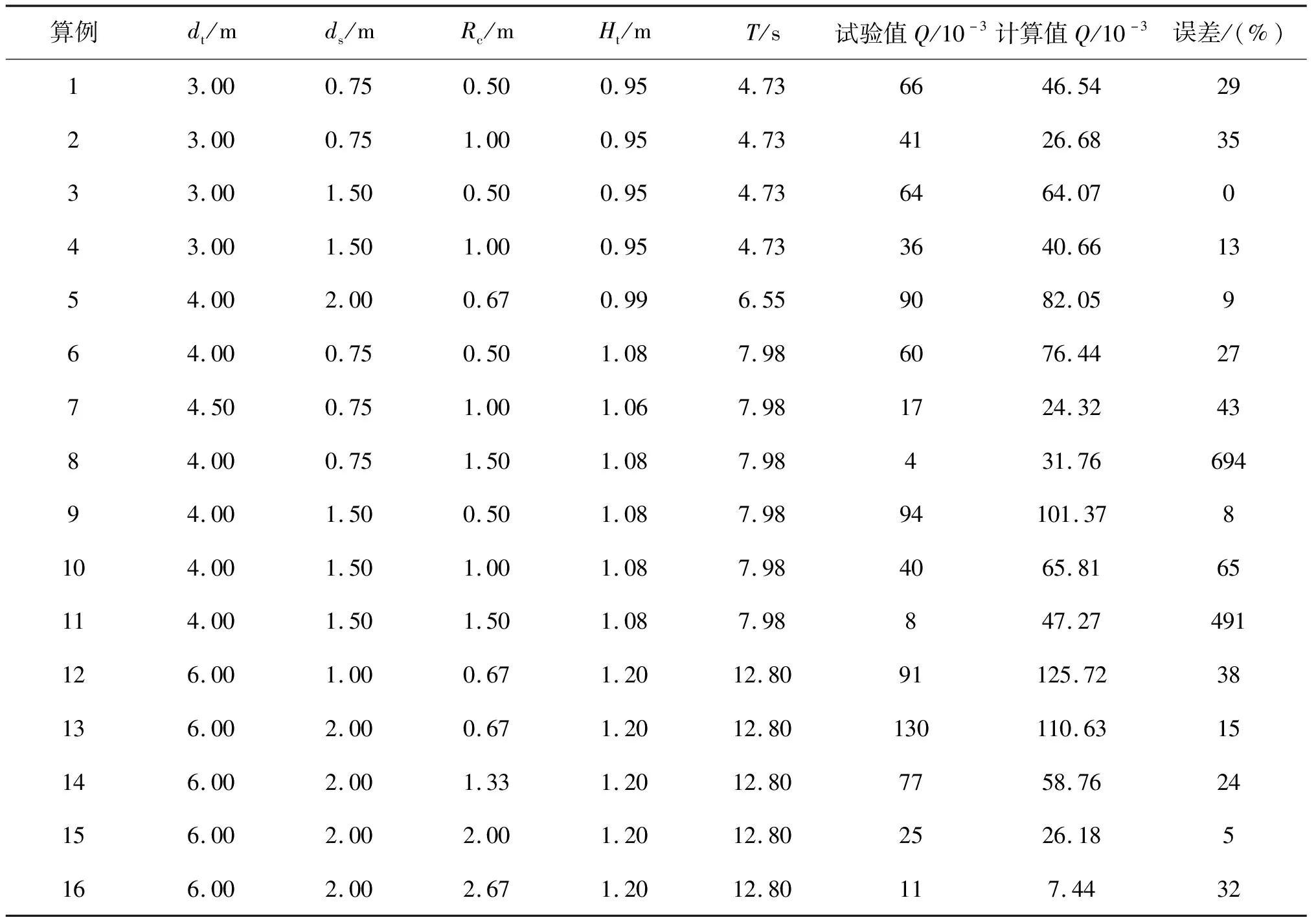
表1 规则波越浪试验条件和结果
在LBM计算中,造波边界距离缓坡堤脚约4倍波长。同物模试验中的统计方法,计算越浪量时去除前几个波浪越浪的结果,取第4至第5个波浪越浪过程Q的平均值作为结果。以算例6为例,由图3的计算结果可以看出,统计时间段内波浪越浪量基本已达到准稳态。
图4为试验值与各模型模拟值的比较,其中LBM的模拟结果整体上与试验数据吻合较好,在合理的精度范围内,表明对越浪的预测没有系统性偏差。最差的结果出现在算例8和算例11中,这两组的越浪量试验值在所有算例中最小,被严重高估。除了Soliman[16]的二维BWNM模型,其他模型在算例8和算例11中也均出现了越浪量被严重高估的现象,且均为偏差最大的组(如图4所示)。Soliman[16]的模型中越浪量被严重高估的两组为算例11和算例7,其中算例7同样为越浪量试验值较小的情况。
对于其他算例LBM计算的平均偏差为24.50%,同样去除算例8和算例11的情况下Shao等[4]和Ni等[5]的SPH模型的平均偏差分别为18.88%和17.20%。闫科谛[1]采用OpenFOAM模型仅计算了算例1~11,故剩余9组的平均偏差为24.38%。Soliman[16]去掉误差最大的两组后平均偏差为20.24%。由以上数据可见,SPH模型的越浪量模拟误差最小,各数值模型的预测水平基本相当,LBM的模拟结果略差于其他数值模型。
各模型在越浪量较小,越浪过程中破碎比较剧烈的情况下模拟偏差均较大,可能与实验室在越浪较小时测量误差较大有关[4-5]。LBM相较于其他模型误差偏大的原因还在于二维条件下LES紊流模型不完全适用,未来可以通过引入RNG k-ω等模型来改善模拟结果。另外,与采用拉格朗日法的SPH模型相比,LBM、BWNM、OpenFOAM模型均采用欧拉网格法,使用的基于VOF方法的自由表面模型仅为一阶精度,精度较低,在处理自由表面问题方面的性能比不上SPH模型,因此模拟误差较大。未来可进一步在LBM中开发高精度的自由表面模型来弥补此不足。

图3 算例6的各个周期的平均越浪量
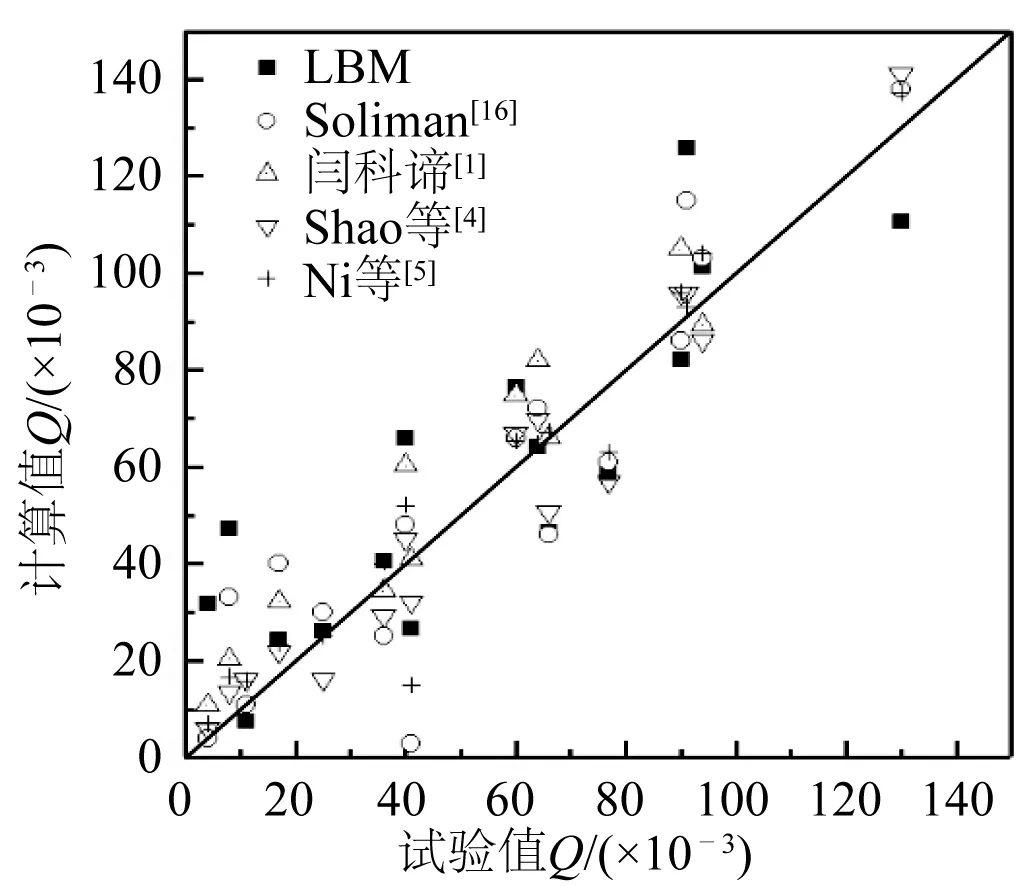
图4 规则波作用下不同模型越浪量计算值与试验值比较
2.2 光滑斜坡堤上不规则波的越浪模拟
Van der Meer和Janssen[17]针对不规则波作用下海堤越浪进行了大量试验,并进一步建立了越浪公式。Soliman[16]和Shao等[4]分别利用Van der Meer和Janssen[17]试验数据对其二维BWNW模型、ISPH模型进行了进一步验证。这里也将使用二维LBM模型对不规则波作用下坡度为1∶1、1∶2和1∶4的光滑不透水斜坡堤越浪进行模拟,并将计算结果与Van der Meer和Janssen[17]试验值及其他模型模拟值进行比较。
试验断面如图5所示,各算例静水深dt均为8.0 m,其中Rc为干舷高度,造波边界距离斜坡堤堤脚约3倍有效波长。采用Goda[18]修正的Jonswap谱生成不规则波,波谱增强因子γ=3.3。在计算中,频谱由50个分量频率表示,有效频率范围为0.5fp至3.5fp,fp为谱峰频率。各算例详细参数如表2所示,其中Hs为有效波高,Tp为谱峰周期,Tm为平均波周期。
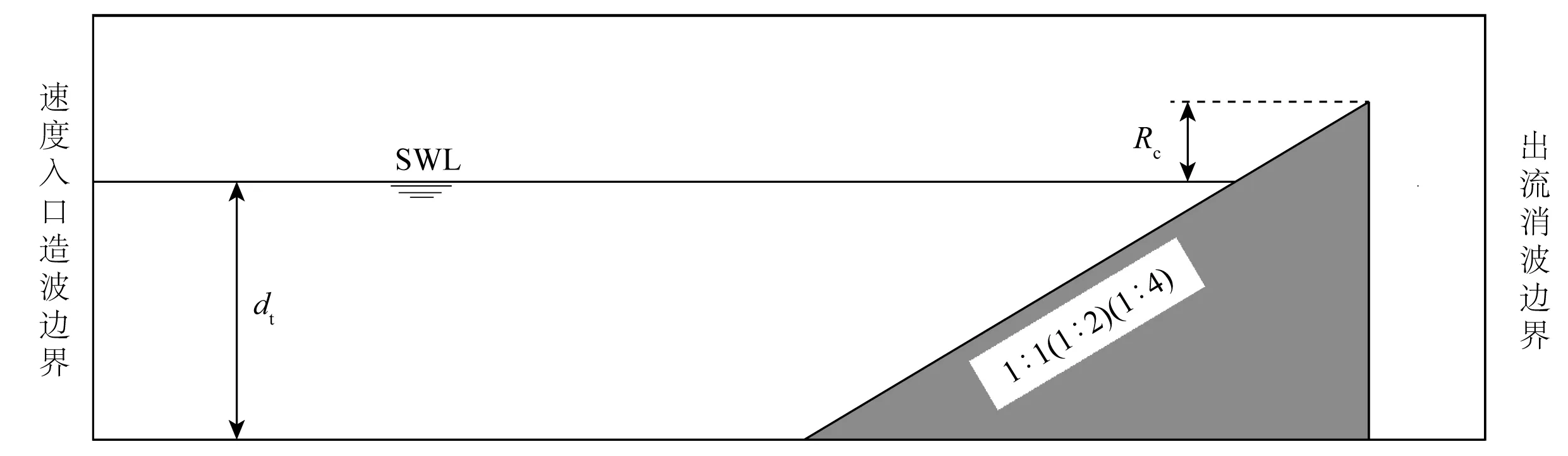
图5 不规则波作用下斜坡堤断面

表2 不规则波越浪试验条件和结果
算例4的累计越浪量历时曲线如图6所示,从图中可以看出不规则波越浪表现出明显的随机性,各个周期的越浪量明显不同,因此采用平均越浪量q作为评价指标研究不规则波越浪。根据Soliman[16]的研究,模型运行30 s左右波浪越浪量趋于稳定。Shao等[4]在SPH的计算中发现越浪需要50 s的时间才能变得稳定,故采用50~180 s内的模拟结果计算平均越浪量。在LBM计算中,发现需要15Tp的时间越浪过程才能稳定,即66.45~91.20 s的时间。图7为从15Tp开始统计的算例4的平均越浪量历时曲线,可以看出255Tp以后平均越浪量开始趋于稳定,因此文中取15Tp~315Tp时间段内的结果来计算平均越浪量。
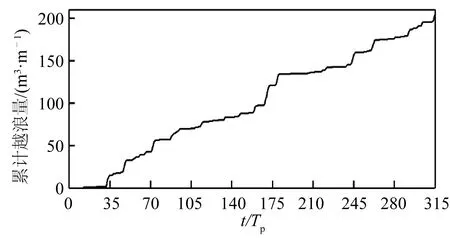
图6 算例4的累计越浪量历时曲线
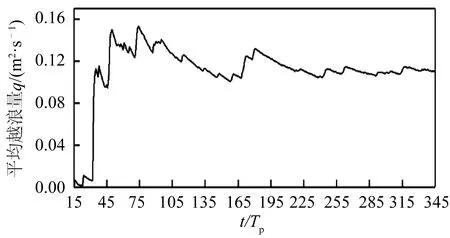
图7 算例4的平均越浪量历时曲线
图8显示了LBM的模拟结果与Van der Meer和Janssen[17]实验室数据,以及Soliman[16]利用BWNM模型模拟结果和Shao等[4]利用ISPH模型模拟结果的对比。结果表明,各个模型均能较好地预测平均越浪量。LBM的预测平均偏差为19.31%,相比之下,BWNM模型的预测平均偏差为27.77%,LBM模型的模拟结果略优于Soliman[16]的模型。SPH模型仅计算了坡度为1∶1和1∶4的算例,故算例1~4与算例10~11的平均偏差为15.44%,预测的准确性方面在三个模型中表现最好。
根据Soliman[16]的描述,越陡的海堤越容易产生非破波越浪,而越平缓的海堤越容易产生破波越浪。这与图9和图10所示的坡度分别为1∶1、1∶4的算例4、算例10的越浪过程波面图相一致。LBM对于坡度为1∶1、1∶2、1∶4算例的平均偏差分别为11.18%、12.52%、52.53%,由此可以看出LBM对于破碎情况越剧烈的越浪,模拟误差越大。因此,可以进一步提高LBM自由表面模型的精度以及开发合理的二维紊流模型来改善破碎波模拟结果,进一步改善LBM模拟精度。
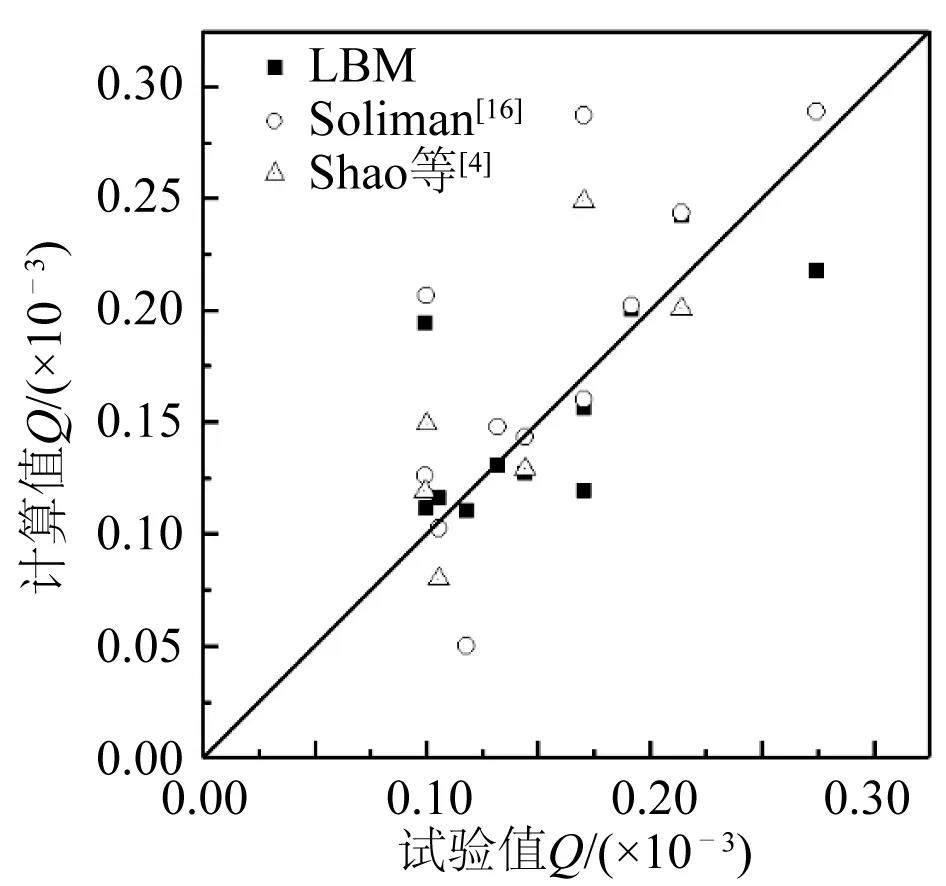
图8 不规则波作用下不同模型越浪量计算值与试验值比较

图9 算例4的越浪过程波面图

图10 算例10的越浪过程波面图
3 结 语
采用刘光威[13]基于LBM方法建立的二维数值波浪水槽,通过主动吸收式速度入口造波,出流边界消波的方法对光滑斜坡堤在规则波与不规则波作用下的越浪进行了模拟,模拟结果与试验值吻合较好,与N-S方程模型和SPH模型模拟精度基本相当,证明了此模型具有模拟斜坡堤越浪的能力。若要对小越浪量等波浪破碎剧烈的情况实现更为准确的模拟,LBM模型还需要进行不断发展与完善,进一步提高自由表面模型的精度以及开发更为适用的二维紊流模型。
就计算时间来看,LBM具有较高的并行计算效率,与基于不可压缩N-S方程的传统CFD模型和SPH相比有更好的并行可扩展性[13]。以文中的不规则波算例为例,这些算例的模拟均在“天河1-A”超算平台上进行,使用未加密的均匀正方形网格,如算例4模拟时间共1 915.2 s,使用48个CPU核,模拟网格数为91 540个,计算用时为30 min。LBM数值波浪水槽的建立有望为研究原型尺度的三维波浪和结构物相互作用提供更为迅捷的模拟手段,值得进一步推广。
