后挖沟深度对深海海底管道屈曲影响数值分析
2020-06-14李修波刘可安王华昆王鸿飞
李修波,刘可安,王华昆,王鸿飞
(1.上海中车艾森迪海洋装备有限公司,上海 200240; 2.株洲中车时代电气股份有限公司,湖南 株洲 412001; 3.天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
目前,海底管道仍是海上石油和天然气最可靠和最有效的运输方式之一[1-3]。为避免铺设于海床之上的海底管道遭受不必要的损伤(海浪、沉积物、抛锚、拖网等),需要将海底管道挖沟埋设于海床之下一定深度[4]。此外,挖沟埋设还可起到对管道保温、为管道可能产生的竖向整体屈曲提供一定的阻力等作用[5-6]。当前,海底管道的埋设方式主要有预挖沟埋设、边铺管边埋设和后挖沟埋设[7]。随着海底管道服役水深的增加,深水环境下的埋设方式主要为后挖沟埋设,海底管道靠等效自重坠入沟底,管道沟自然回填。海底挖沟机是管道后挖沟埋设的主要设备,主要有水力冲射式、机械式和犁式[4]。对于深水环境,水力冲射式挖沟效率较低,挖沟设备较复杂[4];而犁式挖沟机在深海环境下性能卓越,适用范围广[8]。SMD公司在海底管道、电缆挖沟埋设方面,设计出多种系列型号的海底挖沟机,SMD拥有的水下挖沟犁产品代表了世界挖沟技术的先进水平[9-12],如MPS、APP、AMP、VMP,挖沟深度可达1.8 m、2.5 m或更深,管道外径可达700~1 460 mm。
采用犁式挖沟机进行管道后挖沟埋设的过程中,需要预先利用机械手将海底管道抬离海床一定高度,放置于托管架上;在挖沟、埋设过程中,海底管道在托管架与沟底之间始终存在一段距离的隆起悬跨;此时,海底管道出现大挠度变形,导致截面椭圆化,在深水外压作用下极易产生局部屈曲失效[13-14]。后挖沟深度H是海底挖沟机的一个重要工程设计参数,同时,其也是影响管道悬跨屈曲程度的一个重要因素。在对SMD现有犁式挖沟机参数后挖沟深度H优化的过程中发现,优化的前提条件是挖沟过程中存在的悬跨在外部静水压力作用下,不会导致管道发生屈曲破坏,也就是说,首先要确保挖沟埋设的过程中不会对海底管道产生额外的损伤。
对于海底管道的悬跨问题,Brazier[15]在弹性范围内对海底管道在弯矩和拉力组合作用(如海底管道的铺设)下的非线性屈曲响应进行了分析,主要侧重于管道铺设段的屈曲失效;对犁式挖沟机挖沟埋设过程中造成的悬跨问题,王红平[16]、郭钽[17]、迟令宝[18]和于贵芙[19]分别从理论分析、有限元仿真等方面展开了研究,主要侧重于悬跨是否对管道产生塑性损伤。在挖沟埋设的过程中,海底管道除了遭受管道重力和安装作用力,还遭受外部静水压力。上述研究并未对挖沟埋设造成的管道悬跨(管道截面椭圆化)在遭受外部静水压力作用下的屈曲压溃问题展开分析研究。同时,目前很少有研究涉及建立在外部静水压力下,遭受集中力造成的悬跨段(管道后挖沟埋设)的屈曲压溃响应的关系表达式。
因此,采用ABAQUS软件,分别建立了作业前和作业中两种工况下的悬跨模型,分析了机械手对接触部分管道的损伤;进一步,建立作业中不同管径和不同后挖沟深度下的管跨局部屈曲数值模型,对处于外部静水压力作用下的悬跨管的屈曲失效展开分析;最后,在后挖沟深度与外部静水压力组成的区域内,建立临界关系曲线,并划分出工作区和压溃区,为深海管道后挖沟埋管的施工提供工程参考。
1 后挖沟埋设海底管道有限元模型
采用海底挖沟犁对海底管道进行后挖沟埋设的过程中,在挖沟机挖沟作业之前,需要将预先铺设于海床之上的海底管道提升一定的高度,放置到托管架,形成悬跨段,如图1(a)所示;在挖沟铺设作业过程中,海底管道始终存在从挖沟机托管架到沟底的悬跨段,如图1(b)所示。
Brazier[15]研究了管道在纯弯曲作用下的屈曲问题,推导出了屈曲公式;同时,Brazier也指出,在出现纯弯曲作用下的屈曲失效之前,管道截面出现了椭圆化,如图2所示。因此,根据海底挖沟机的作业特点和流程,需要对遭受多种载荷的海底管道,在不同作业阶段形成的管跨段(管道截面椭圆化)进行相应的分析,确保其在挖沟埋设过程中安全可靠。

图1 作业前和作用中海底管道悬跨示意

图2 管道屈曲压溃前管道截面椭圆化示意
相关模型数据以SMD AMP500[11]挖沟犁为例,托管架间距ΔL=18 m;作业时前托管架距海床最低高度ΔH=0.2 m;后挖沟深度H=1、1.5、2、2.5、3、4 m(其中,1、1.5、2、2.5 m是该型号挖沟机可达到的挖沟深度,3、4 m为数值分析数据),简化模型如图3所示。

图3 作业前和作业中管道悬跨示意
目前,我国主要选用标准为API的单层结构管道进行铺设,文中主要研究对象为单层管道。采用API X65型管道进行数值分析,模型参数见表1[20]。在后挖沟埋设过程中,鉴于海底管道自然落入沟内,须确保海底管道的负浮力状态,为便于数值分析,这里取等效加速度g=9.8 m/s2。

表1 API X65管道参数
建立后挖沟状态下管道受力分析的有限元模型,采用静力分析,以准静态的方式模拟悬跨对压溃压力的影响。根据管道受力模型特点,可建立1/2对称模型,以降低计算成本。管道采用壳单元S4R模拟,壳单元沿厚度方向取7个积分点,海床与机械手均设为刚体,不考虑其变形;管道与机械手、管道与海床均设为硬接触,不考虑管土之间的相互作用。将管道剖分为5部分,根据网格收敛性检验,最终机械手加载区单元取0.1 m,两段区域单元取2 m,中间区域单元取0.8 m,如图4所示。对管道对称面设置对称约束,管道的一端设置成固定约束;另一端仅限制X方向位移,不限制重力方向(Y向)和轴向位移。数值模拟过程中,先对模型施加沿Y轴负向的重力载荷,使其自然下垂至沟槽中;然后通过托管架提升管道,模拟抓举过程导致的截面变形;最后施加外部静水压力,计算对应变形截面的局部屈曲载荷。

图4 网格划分示意
在采用ABAQUS进行有限元模型的过程中,材料的应力应变曲线采用Ramberg-Osgood(R-O)模型来表示。R-O模型如下:
(1)
式中:参数采用试验得到的数据[20],n为10.7,σy为448 MPa。
为了研究挖沟深度对管道压溃的影响,分别模拟作业前和作业中机械手对悬跨管道的损伤,再以准静态的方式分析悬跨导致的局部椭圆化对管道压溃压力的影响。
1.1 机械手对预铺设管道的损伤模型
机械手将预铺设于海床之上的海底管道抬升起一定高度,造成悬跨管道,建立作业前(图5(a))和作业中(图5(b))两种状态的数值模型。

图5 作业前和作业中海底管道悬跨示意
1.2 后挖沟深度对压溃压力的影响模型
研究的主要内容是后挖沟埋设深度与管道所处外部静水压力作用下的海底管道屈曲失效的关系,所遭受的环境载荷主要为管道自重、浮力、抬升部位的托举集中力和管道外部静水压力。对于实际管道,管道服役环境始终遭受外部静水压力,当机械手抬升预铺设的管道时,若造成管道悬跨过大(管道截面椭圆化过大),可能会造成管道的局部屈曲进而引发屈曲传播,导致大面积的管线破坏。因此,需要进一步研究悬跨管道对压溃压力的影响,数值模型如图5所示。
2 有限元结果分析
2.1 机械手对预铺设管道的损伤
作业前和作业中,悬跨段受力分析,分别如图6、图7所示。

图6 作业前管道悬跨部分的应力分析示意

图7 作业中管道悬跨部分的应力分析示意
在未施加水压的情况下,机械手将海底管道抬升一定高度,造成管道悬跨,致使管道截面椭圆化。对同一提升高度(托管架间距18 m,提升高度H+ΔH=2.2 m)下的作业前和作业中的静力分析,造成管道出现最大应力的位置相同,但最大应力值不同(作业前σmax=258.5 MPa;作业中σmax= 287.5 MPa),作业中造成的悬跨比作业前造成的悬跨对海底管道的损伤更大,这一结论与文献[16-17]一致。
分别对不同挖沟深度和不同管径下,管道与机械手接触部分损伤情况展开数值分析,结果如图8所示。对于同一挖沟深度下不同管径的管道,管径越大,管道与机械手接触部分的应力越大;对于同一管径的管道,随着挖沟深度的增加,管道与机械手接触部分的最大应力值不断增加,管道截面椭圆化越严重。
当机械手与海底管道接触部分的应力值小于管道钢的塑性极限时,管道截面材料虽未进入塑性阶段,但管道截面发生椭圆化,如图9所示。此时,管道将产生弹性变形,载荷卸载时,管道可恢复至初始状态(管道埋入海床一定深度时,管道截面可恢复至正圆的初始状态)。
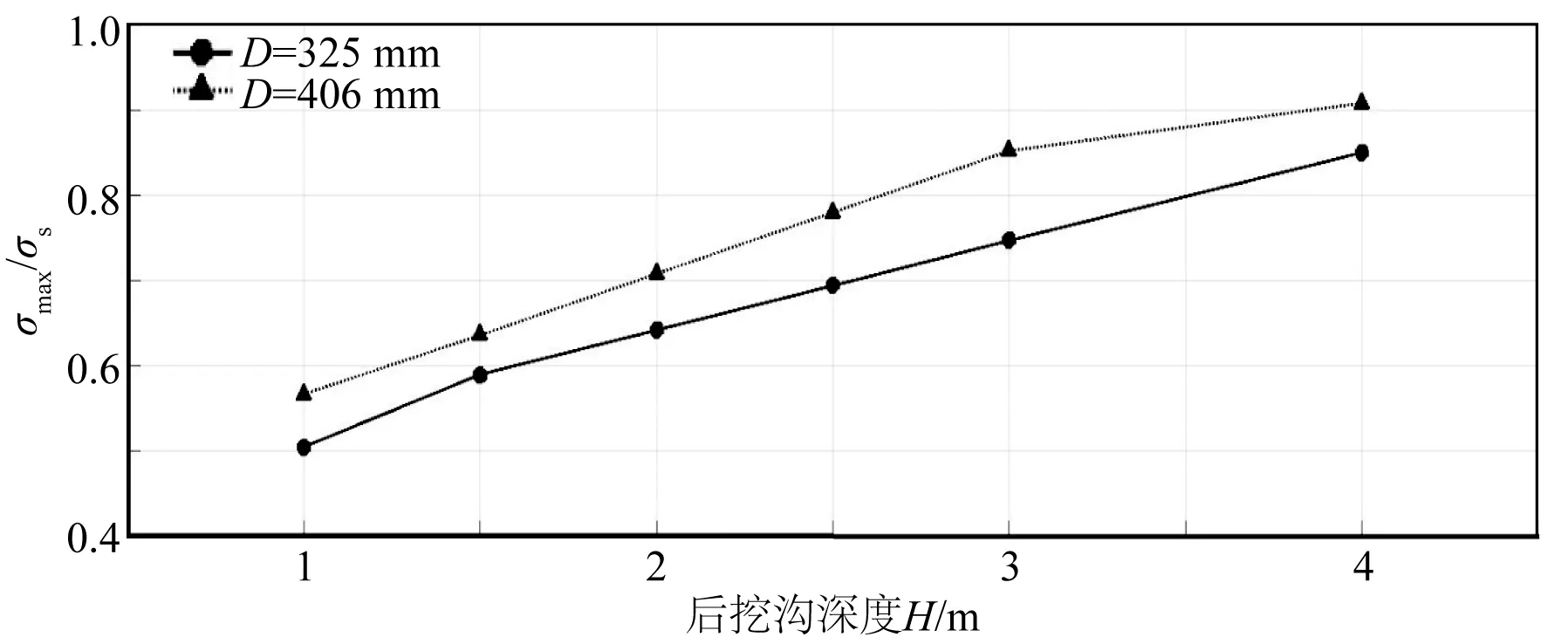
图8 作业中不同管径下的后挖沟深度与管道悬跨部分应力比之间的关系

图9 作业中悬跨段管道截面椭圆化示意
当机械手与海底管道接触部分的应力值大于等于材料的塑性极限时,管道将产生塑性变形,载荷卸载时不可恢复到初始状态(管道埋入海床一定深度时,管道截面依旧保持椭圆形)。利用参数α来表示管道的安全裕量,安全裕量α的表达式如下:
(2)
式中:σmax为作业中管道与机械手之间的最大应力值;σs为管道的屈服强度。当α≤0时,管道的上的应力最大值σmax≥σs,即管道进入塑性变形状态。
同时,对上述参数拟合,建立不同管径下后挖沟深度与安全裕量α之间的关系曲线,如图10所示。在文中对于管径D=325 mm而言,当H/D=17.5(托管架间距18 m,后挖沟深度H=5.7 m)时,管道变形将进入塑性变形区域,也就说,当挖沟深度H<5.7 m时,管道还处于弹性变形阶段,但管道截面呈现椭圆形。

图10 作业中不同管径下后挖沟深度与安全裕量α之间的关系曲线
2.2 后挖沟深度对压溃压力的影响
后挖沟深度H的增加,不但增加了悬跨的高度(H+ΔH)(如图3(a)所示),还增大了机械手对悬跨管道接触部分的应力(如图8所示)。悬跨段接触部分的应力不断增加,加剧了截面的椭圆化,如图9所示;管道截面的椭圆化,是影响管道压溃压力的一个重要因素[13-14]。在模拟过程中,在机械手将管道提升一定高度之后,对管道施加外部静水压力,进而模拟后挖沟深度对管道压溃压力的影响。
由2.1结论可知,机械手在作业过程中对海底管道造成的悬跨对管道产生的损伤更大,在此基础之上,研究作业中后挖沟深度对压溃压力的影响,如图11所示。进一步分析可知,管道与机械手接触的位置出现最大的接触应力,即塑性压溃位置首先在此处出现。

图11 作业中管道悬跨压溃示意
分别对不同后挖沟深度和不同管径下,管道与机械手接触位置处出现塑性压溃的临界压力展开系统分析。文中通过参数β来表示不同后挖沟深度和不同管径下,悬跨管道出现临界压溃的难易度。难易度β的表达式如下:
(3)
式中:Pc为作业中悬跨管道出现临界压溃时的水压。
对于同一后挖沟深度下的不同管径的管道,管径越大,管道与机械手接触部分出现压溃的压力更小,也就是说,管道越粗,越容易出现管道的压溃失效,结果如图12所示;对于同一管径的管道,随着后挖沟深度的增加,机械手对管道的损伤加大,即管道的安全裕量减小,如图10所示,管道出现塑性压溃的临界压力值也不断降低,如图12所示。

图12 作业中不同挖沟深度下与临界压溃压力的关系
同时,对上述参数拟合,建立不同管径下后挖沟深度H/D与难易度β之间的关系曲线,如图13所示。在文中对于管径D=406 mm而言,当H/D=13(托管架间距18 m,挖沟深度H=5.278 m)时,悬跨段管道的最大应力只要达到管道的塑性极限,管道就会进入屈曲失效阶段。

图13 作业中不同管径下后挖沟深度与难易度β之间的关系曲线
3 后挖沟深度与管道外部静水压力的关系分析
在MATLAB中选择不同的拟合方式,通过比较,线性拟合的偏差值最小,进而得到拟合表达式。后挖沟深度与临界压溃压力的关系建立如下数学表达式:
(4)
式中:a、b拟合参数。
以管径D=325 mm为例,后挖沟深度与临界压溃压力的临界关系曲线,如图14所示。临界关系曲线将后挖沟深度与外部静水压力组成的区域分为安全工作区和压溃区两部分,临界曲线的左下部分为安全工作区,右上部分为压溃区。

图14 作业中后挖沟深度与临界压溃压力的临界关系曲线示意
4 结 语
通过对犁式挖沟机的后挖沟深度对压溃压力的影响展开系统分析,可得到以下结论:
1)犁式挖沟机的机械手使海底管道出现一定的悬跨段,机械手与悬跨段管道接触之间的应力随管道外径的增大而增大;接触部分的悬跨管变形虽未进入塑性区,但管道截面发生椭圆化。
2)犁式挖沟机的后挖沟深度对悬跨段管道出现压溃的压力值产生影响,后挖沟深度越大,临界压溃压力值越小;不同管径的悬跨段管道出现压溃的压力值随后挖沟深度的变化趋势是一致的。
3)犁式挖沟机的后挖沟深度与临界压溃压力的关系基本呈现线性关系;文中建立的临界压溃压力与管径、屈服极限和后挖沟深度的函数表达式,为工程施工提供参考。
