0-1整数规划问题的DNA四面体步行者计算模型

杨新木，杨 静*，殷志祥，唐 震，崔建中

(1.安徽理工大学 数学与大数据学院，安徽 淮南 232001；2.上海工程技术大学 数理与统计学院，上海 201620；3.安徽理工大学 电气与信息工程学院，安徽 淮南 232001；4.淮南联合大学 计算机系，安徽 淮南 232001)

近年来由于科技高速发展，传统的电子计算机存储量小，计算速度不够快，科学家们正努力寻找其他运算速度更快。存储量更大的新型计算机，如量子计算机、人工神经网络计算机等。1994年，美国加利福尼亚大学Adleman[1]博士利用DNA编码解决了图论中的NP完全问题——有向图的Hamilton路径问题。分子自组装的原理是利用分子与分子或者分子中某一片段与另一片段的分子识别，相互通过非共价作用形成具有特定排列顺序的分子聚合体。DNA分子结构特征和独特的分子间的相互作用，非常适合作为自组装的材料，可以合成一系列具有复杂结构的物质。2006年，Rothemund[2]提出了一种全新的DNA自组装的方法——DNA折纸术，通过DNA折纸术，Rothemun得到了三角形、方形、矩形、五角星、笑脸等精细复杂的二维结构，如图1所示。2010年，Pei[3]等人首次构建出新型三维纳米结构的DNA探针自组装平台，该平台具有合成简单，稳定性好和产率高等优点。2017年，Tikhomirov[4]采用微米级DNA折纸阵列，成功描摹蒙娜丽莎和公鸡等图像，并发现自组装成阵列不受瓦片表面图案变化的影响。2019年，晁洁等[5]利用DNA自组装设计了一种DNA导航器系统，该系统可以在二维DNA折纸平台上定义的十个顶点根树上执行单分子并行深度优先搜索。

图1 DNA折纸术图形

本文利用DNA折纸术[6]构建一个DNA四面体步行者，并将其应用于求解0-1整数规划问题。该模型利用DNA折纸术和探针技术，可以大大降低普通的自组装模型所造成的困扰，从而进一步提升DNA计算模型的准确性。

1 DNA折纸术和0-1整数规划

1.1 DNA折纸术和DNA四面体

1.1.1 DNA折纸术

DNA具有结构稳定、易识别、容易操作等优点，一直是科学家们研究的热点。DNA折纸术的原理是将一条较长的DNA单链(通常称为脚手架链)与经过一系列步骤设计的较短的DNA片段(通常称为订书钉链)，通过碱基互补配对原则能够可控地构造出高度复杂的纳米图案或结构，在新兴的纳米领域中具有广泛的潜在应用。DNA折纸术与传统的DNA自组装相比，更容易组合出结构稳定、高度复杂的纳米结构，并具有纳米可寻址性。Shih[7]等人采用DNA折纸术的方法，首次制造出三维结构，揭开三维纳米DNA结构自组装的序幕。Ke[8]等人设计出一个空心四面体立体结构。Han[9]等设计和构建自组装DNA纳米结构，利用DNA折纸术组装了一系列具有高曲率DNA纳米结构。Zhang[10]等人利用DNA折纸术构建出具有高度复杂性和可编程性的有限尺寸线框DNA纳米结构。Gopinath[11]等人利用DNA折纸术定向自组装到光刻图案的结合位点上，使分子发射器与光子晶体腔可靠且可控地耦合。Tang[12]等利用DNA折纸术建立了动态与非门计算模型。同年，王飞[13]等人利用DNA折纸术相继提出多种维度不同模式的荧光阵列构建方案，在生物传感、新型荧光探针设计等领域得到广泛应用。

1.1.2 DNA四面体

DNA四面体结构是利用DNA折纸术通过巧妙的DNA序列设计，应用互补配对原则，各链自动杂交组合而成的具有四面体形状的DNA三维纳米结构，如图2。

图2 DNA四面体结构

Ke[8]等利用DNA折纸术构造了DAN四面体笼，该四面体通过4个三角形的平面进行封闭，三角形的每条边大约是54 nm。它是由多条订书钉链和一条支架DNA杂交，而非彼此杂交，因此反应对计量关系的精确度要求相对较低，这可以显著提高组装的成功率和产量。Li[14]等设计出一种基于DNA四面体的DNA芯片和一种通用的基于DNA四面体的微阵列平台，用于检测不同类型的生物活性分子，体现了DNA四面体在生物传感器方面应用的潜能。林美华[15]设计一种四面体DNA纳米结构探针应用于生物传感器当中，该DNA四面体表面不仅探针多而且还能够精确的控制探针之间的距离，具有传质速率快，灵敏度高等优点。樊春海[16]等人基于DNA纳米结构设计的生物传感器，可以对蛋白质、核酸、小分子以及细胞的高灵敏监测，并能保持优异的检测性。Yang等[17]人先利用折纸术构建DNA四面体，再利用DNA四面体作为基底构建探针，去解决0-1整数规划问题。该模型能够降低伪解的产生，提高求解效率。DNA四面体在分子诊断、分子输送和药物靶向治疗等方面具有良好的应用前景。

1.2 0-1整数规划

整数规划是从1958年由戈莫里[18]提出割平面法之后形成独立分支的。整数规划是线性规划的重要部分。整数规划的一种特殊情形是0-1规划，即变量只取0或1两种的整数规划问题。许多的NP完全问题也都可以转化为0-1规划问题。但是到目前为止任然没有非常好的算法来解决这种问题。

有不少学者先后利用DNA计算尝试解决0-1规划问题。首次取得突破性进展是殷志祥[19]提出基于表面的DNA计算模型求解一般形式的0-1整数规划问题。朱建鹏等[20]人利用DNA芯片的独特优势，针对特殊的0-1规划给出了DNA计算模型。赵鑫月等[21]人利用DNA折纸术构造订书钉链，与反应溶液中的脚手架链形成二级结构，求解0-1整数规划问题，该方法容易操作，具有很强的并行性。

1.3 0-1整数规划问题的基本算法

步骤1：生成给定问题的变量取值为0或1的所有可能组合，即问题所有的可能解；

步骤2：利用每一约束条件剔除非可行解（保留可行解）；

步骤3：生成生余解；

步骤4：重复进行步骤2、3。我们可以排除所有的非解，从而得到问题的所有可行解；

步骤5：比较各可行解对应的目标函数值，进而得到最优解；

2 0-1整数规划问题的DNA四面体步行者计算模型

2.1 生物算法

步骤1：通过DNA探针找出0-1整数规划问题的所有可能解；

步骤2：通过荧光个数找出第一个满足约束条件的可行解；

步骤3：进一步通过纳米金颗粒个数找到同时满足第一个和第二个约束条件的可行解；

步骤4：重复上述步骤，直到找到所有满足约束条件的可行解；

步骤5：通过目标函数，在所有可行解中找出0-1整数规划问题的最优解。

2.2 DNA四面体步行者

利用折纸术构建DNA四面体步行者，将底边三个DNA单链和DNA四面体固定，分别用F1、F2、F3表示这3个“足”。然后将一段DNA单链其固定在DNA四面体的顶点上作为探针，用于检测与其互补的核酸序列。本文探针分为3个DNA单链小片段，分别用表示，如图3(a)。如图3(b)是一个完整的DNA折纸卡槽，DNA折纸卡槽中包含有3组助行器，每组助行器分别用A1、A2、A3表示，并且A1、A2、A3固定在折纸基底上面。靠近DNA折纸卡槽顶端有3个载着相同的纳米金颗粒的DNA机器，它通过碱基互补配对原理固定在DNA折纸卡槽顶端。3个相同的DNA机器与 3个不同的 DNA 片段（x，y，z）部分互补，3个不同的DNA片段可以携带也可以不携带纳米金颗粒。其中DNA四面体上的探针与完全互补，DNA四面体上的探针与完全互补，DNA四面体上的探针与完全互补。

图3 DNA四面体步行者和DNA折纸卡槽

2.3 DNA四面体步行原理

DNA四面体的3个“足”与DNA链A1、A2、A3部分互补DNA链A1、A2、A3固定在DNA折纸基底上。首先，DNA四面体的2个“足”F1、F2与DNA链A1、A2部分互补，还有一个“足”F3是自由足，详细过程见图4(a)。首先加入DNA链和，其中DNA链与DNA链A1完全互补、DNA链与DNA链A2完全互补、DNA链与DNA链A3完全互补。然后DNA链与A1通过DNA链置换成功把“足”F1解链，F1变为自由“足”，此时DNA链A3与“足”F3链发生碱基互补配对，相当于把足“F3”固定在折纸基底上，DNA四面体步行者往前行走一步并且逆时针旋转，见图4(a)(b)。经过一段时间让其完全反应，其次在加入DNA链和A1，DNA链与A2发生链置换成功的把“足”F2解链，F2变为自由“足”，此时DNA链A1与“足”F1链发生碱基互补配对，相当于把足“F1”固定在折纸基底上，DNA四面体步行者往前行走一步并且逆时针旋转，见图4(b)(c)。经过一段时间让其完全反应，最后再加入DNA链和A2，DNA链与A3发生链置换成功的把“足”F3解链，“足”F3变为自由“足”，DNA链A2与“足”F2链发生碱基互补配对，相当于把足“F2”固定在折纸基底上DNA四面体步行者往前行走一步并且逆时针旋转，见图4(c)(d)。重复以上过程，DNA步行者可以在DNA折纸基底上以逆时针120°完成行走。DNA四面体步行者在折纸卡槽中步行一周如图5。

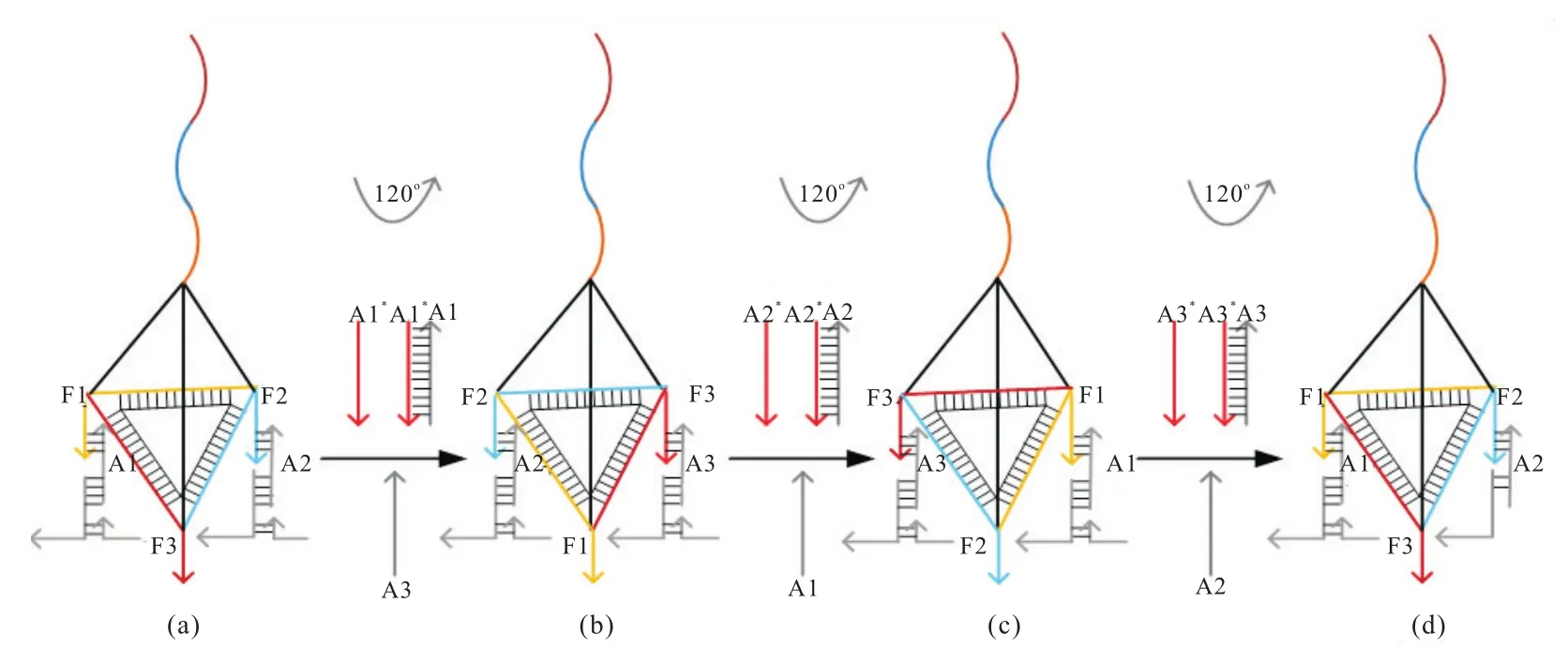
图4 DNA四面体步行者原理图

图5 折纸卡槽中DNA四面体步行者过程图

2.4 实例分析

讨论如下0-1整数规划的DNA计算模型。

步骤1：生成变量的所有的可能解。因为实例分析中的0-1整数规划问题含有3个变量，每个变量都有2种取值（0或1），所以一共有23个可能解。首先利用DNA折纸术折叠出带有探针的DNA四面体步行者和DNA折纸卡槽，DNA折纸卡槽中固定有3个助行者和3个相同的DNA机器，DNA 机器与不同 DNA 片段（x，y，z）部分互补，DNA片段可以携带纳米金颗粒也可以不携带纳米金颗粒，故共有23种可能，并且DNA片段（x，y，z）携带的纳米金颗粒分别与DNA四面体上的探针x*,y*,z*完全互补。探针上携带有纳米金颗粒记为1，没有携带纳米金颗粒的记为0。

步骤2：用23个DNA四面体步行者在载有不同的DNA折纸卡槽的折纸基底行走，经过一段时间，可得到该问题的所有可能解。如2号解，DNA机器上只有DNA片段x携带纳米金颗粒，DNA片段y和z都不携带纳米金颗粒，DNA四面体步行者在助行器上面步行一周，最后探针上只有x携带有纳米金颗粒，所以x取1，y和z都取0，这样就得到2号解，详细过程见图6。类似地，可得到(x,y,z)取值的所有可能解，分别为1号解(0,0,0)、2 号解(1,0,0)、3 号解(0,1,0)、4 号解(0,0,1)、5 号解(1,1,0)、6 号解(1,0,1)、7 号解(0,1,1)、8 号解(1,1,1)。这8种可能解对应的DNA四面体步行者所携带的纳米金颗粒的个数和位置如图7。

图6 2号解的示意图

图7 8种可能解

步骤3：删除不满足约束条件的解。对第一个约束条件，DNA四面体探针上的纳米金颗粒要大于等于 2，满足条件的有 5，6，7，8 号解；对第二个约束条件，由于约束条件不涉及变量y，所以y位置中的纳米金颗粒不再考虑。只考虑5，6，7，8号解，DNA四面体上的探针x和z的纳米金颗粒数量要小于等于1，即为满足第二个约束条件的可行解，它们是5或7号解；对第三个约束条件，只考虑5，7号解，只要考虑DNA四面体上的探针y和z的纳米金颗粒数量要小于等于1，即为满足第三个约束条件的可行解，即5号解，同时也满足第一个和第二个约束条件，所以可行解只能是5号解。

步骤4：得到满足该约束条件的可行解，实例分析中的可行解只有5号解，同时也是唯一解，5号解也是最优解，目标函数的最小值为5。5号解得结构示意图如图8。

图8 解的示意图

2.5 复杂度分析

模型的复杂度通常包括时间复杂度和空间复杂度。时间复杂度通常与其生化反应时间有关，由于生化反应具有很高的并行性，这是传统计算机所不具备的能力。空间复杂度通常与其计算深度有关。该模型中使用的DNA短链数与变量的表示形式和变量数有关，模型的计算深度与模型的约束有关，因此模型的复杂度与变量n呈线性关系。以上分析表明，该模型大大降低了整数规划问题的复杂度，是一种较为有效的模型。

3 小结

本文基于DNA折纸术设计了一个DNA四面体步行者计算模型，结合DNA链置换和纳米金颗粒来搜寻0-1整数规划问题的最优解。DNA折纸术和DNA链置换是DNA自组装中最重要的两种技术手段。基于DNA折纸术和DNA链置换所设计的计算模型，有如下优点：首先，结构简单，可以解决多个变量的0-1整数规划问题，具有很好的通用性。其次，DNA四面体上的探针具有高度特异性、高度灵敏性、较好的可控性，而且效率高，没有副产物，错误率非常低。最后，用纳米金颗粒易于标记并且对DNA链置换几乎没有任何影响，很容易观察到最后DNA四面体上的探针上的纳米金颗粒的位置。