差分吸收光谱测量臭氧浓度信号去噪的实验研究

郑海明，刘 佳

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

1 引 言

随着国家对火电厂污染物排放的要求越来越严格，臭氧同时脱硫脱硝技术凭借投资和运行成本廉价、系统简单、占地面积小等优点，已成为烟气污染物控制技术的发展趋势[1]。在实施这项新技术的同时，臭氧浓度在线监测必不可少。差分吸收光谱(DOAS:differential optical absorption spectroscopy)法的本质是基于分子对光辐射的选择性吸收，将臭氧的吸收带分为随波长慢变化的“宽带吸收带”和随波长快速变化的“窄带吸收带”。其中窄带吸收主要是由于臭氧分子的特征吸收造成的，宽带吸收主要是由于分子的米氏散射与瑞利散射引起的。差分吸收光谱技术的关键就在于如何准确获得所测气体的特征吸收光谱[2]。

在实际的气体测量中，环境和仪器本身的噪声会对臭氧的吸收光谱造成很大的影响，从而影响后期特征光谱的获取，导致测量结果不准确。常用的去噪方法有：小波变换、Savitzky-Golay滤波和傅里叶变换滤波。小波变化具有很好的时频局域特性，能通过伸缩和平移对信号进行多尺度分析，是一种很好的信号分析手段，本文利用wdencmp函数和wden对信号分别进行了阈值去噪、Savitzky-Golay滤波去噪，在滤波的同时保留了原始光谱的高频分量，从而减少了光谱吸收峰高度和宽度的失真，选用了不同的窗宽对信号进行了处理；傅里叶变换在信号的频域里进行分析处理，滤除噪声的频率后逆傅里叶变换，能很好地滤除高频噪声。对比3种滤波方法处理后的光谱图，信噪比与均方根误差发现Savitzky-Golay滤波具有良好的去噪效果，可以提高臭氧的反演精度。

2 去噪原理

2.1 小波变换去噪原理

一个含噪的一维信号模型可表示为

s(k)=f(k)+ε·e(k)

(1)

式中：s(k)为含噪信号；f(k)为有用信号；ε为噪声系数的标准偏差;e(k)为噪声信号，k=0,1,…,n-1。

在实际工程中，e(k)通常表现为高频信号，f(k)通常表现为低频信号或者一些比较平稳的信号。小波去噪的原理是：对于一个给定的信号，首先把它展开成小波的平移和伸缩之和。高频部分随机噪声的小波系数非常小，可以设定一个阈值，对于小于该阈值的小波系数置零，最后利用处理得到的小波系数重构原信号即可实现去噪[3]。小波变换对信号降噪的实质就是：抑制信号中的无用部分，恢复信号中有用部分的过程。

2.2 Savitzky-Golay滤波去噪原理

Savitzky-Golay滤波即把采集到的光谱数据划分为多个窗口，选取滤波所需要的窗宽和拟合阶次，对窗内的数据进行最小二乘拟合，每一个数据点都用它本身和其周围在窗内的数据点的线性组合来代替。将滤波的窗口向前移动一点，重复以上步骤即可实现降噪。Savitzky-Golay滤波的关键是窗宽和窗内拟合阶数的选择。Savitzky-Golay滤波可以在平滑数据的同时更好地保护高频成分。

2.3 傅里叶变换去噪原理

傅里叶变换滤波，是一种时频转换的数学分析方法。信号通常在频域里表现的更直观，更容易进行分析。其基本变换公式[4]为：

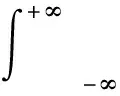
(2)

式中：f(t)为非周期性连续时间信号；F(ω)为信号f(t)的连续频谱；ω为相应的频率。

傅里叶变换滤波的基本思想是把信号分解成一系列不同频率正弦波的叠加，把信号从时域转换到频域，以提取时域信号的频率特征。通过傅里叶变换，得到光谱信号的频率响应信息，变换后频谱图中的高频部分对应的就是光谱信号中的噪音部分[5]。因此，在频谱中界定一点，大于这一点即认为是高频噪声，截取这一点之前的频谱进行逆傅里叶变换从而得到去除噪声后的光谱信号。

3 实验装置

实验通过流量计控制氮气与氧气的配比，利用臭氧发生器产生不同浓度的臭氧来进行研究。图1为测量实验装置的示意图，分别利用搭建的实验台测量通入待测气体前与通入待测气体后的光强。氙灯发出的光通过准直透镜准直后，进入气体吸收池吸收;然后，在另一端的准直透镜汇聚后，进入光纤光谱仪完成数据的采集;最后，将采集到的数据传输到电脑，利用Matlab软件进行分析处理。其中气体吸收池的材料为聚四氟乙烯，可以防止臭氧气体的腐蚀，气体吸收池两端分别与臭氧发生装置和大气相连。

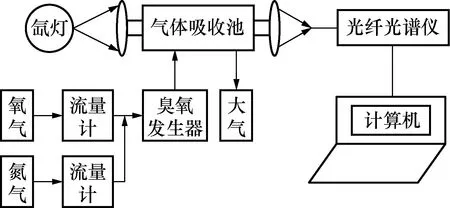
图1 测量实验装置示意图

4 实验吸收光谱的处理

将光谱仪进行预热后，首先测量采集实验的暗电流谱。采集背景谱与通入臭氧气体的吸收谱，在数据处理过程中扣除暗电流的影响，进行臭氧吸光度的计算，如图2所示。

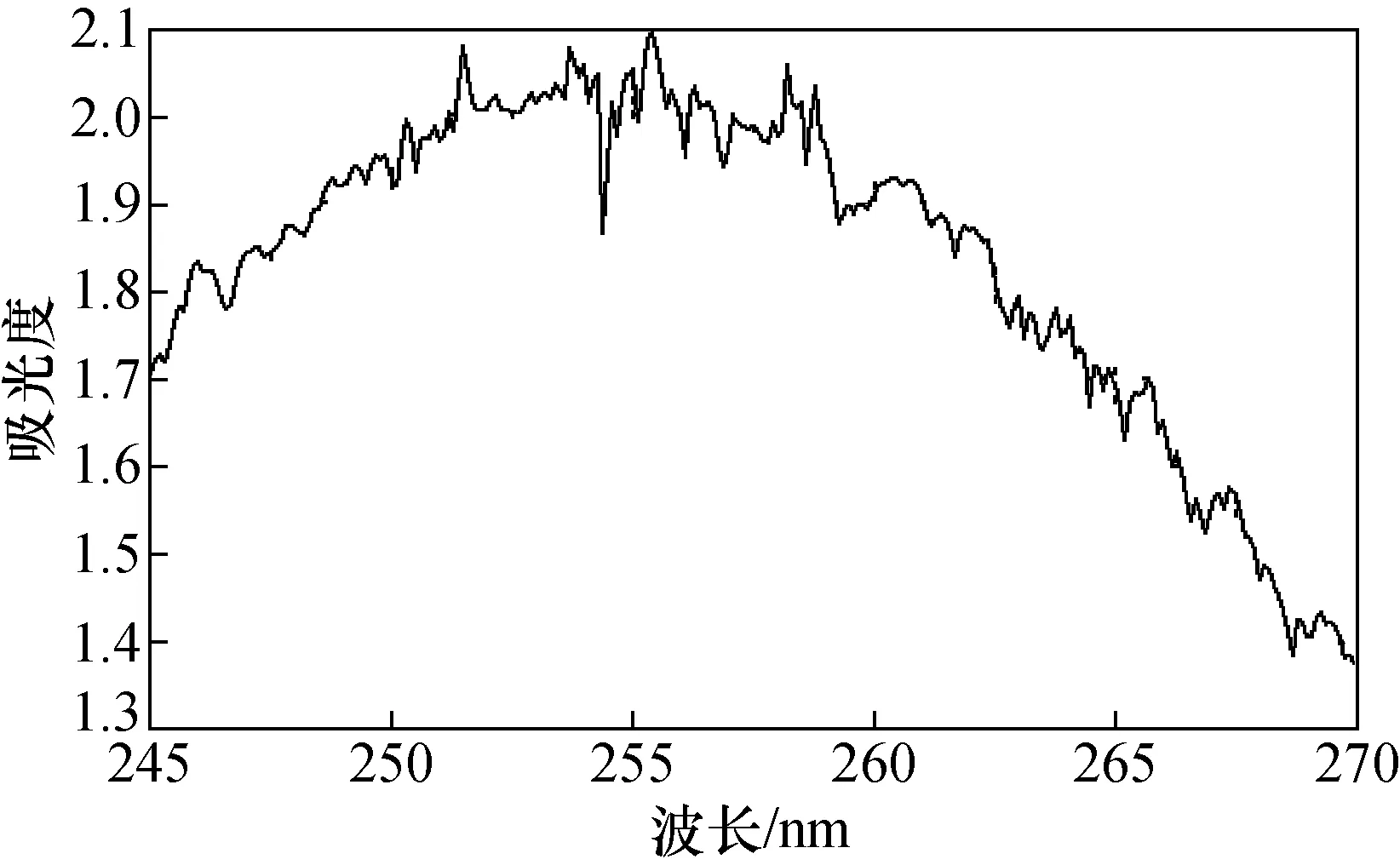
图2 含噪声的臭氧吸光度

4.1 小波变换数据处理

对光谱信号处理比较有效的几种小波系主要包括：Symlets(sym)小波系、Daubechies(db)小波系和Biorthogonal(bior)小波系。其中对于污染气体去噪最常用的是db小波母函数。本文采用常用的db5小波作为小波母函数，小波分解层数为2，对信号进行了阈值去噪。关于阈值函数的选取，张磊等[6]提出在实际应用中硬阈值效果往往更好，可以很好地保留信号边缘等局部特征。邵理堂等[7]也提出当有效信号的幅度和尺度与噪声相差不大时，使用硬阈值效果较好。本文阈值函数选择了硬阈值函数。

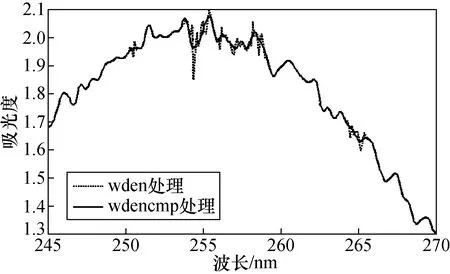
图3 wden与wdencmp函数去噪后的臭氧吸光度

首先选择了利用ddencmp函数产生信号默认阈值，之后利用wdencmp函数进行信号去噪处理，实验结果如图3实线所示。本文进一步选择了自动去噪函数wden对信号进行去噪，此时小波去噪的自适应阈值选择规则包括rigrsure阈值、heursure阈值、sqtwolog阈值、minimaxi阈值。与rigrsure阈值和minimaxi阈值相比，heursure阈值和sqtwolog阈值更加灵活，能够根据不同层的噪声调整阈值，在信号去噪方面更加有效，可以提取出微弱信号[8]。从特征信号提取的角度考虑，选择了heursure阈值，实验结果如图3虚线所示。wdencmp函数和wden函数是小波去噪最常用的函数。通过图3发现，利用两种函数进行滤波处理后的波形，在与原图保持了较高相似度的同时，均取得了良好的去噪效果；两种函数处理后的波形基本吻合，在细节处理方面略有不同。通过图4的放大图发现，wden函数更多地保留了信号的突变部分，wdencmp函数相对更加平滑。

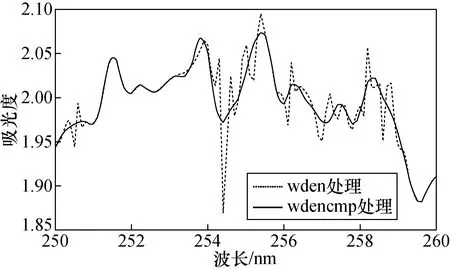
图4 wden与wdencmp函数去噪后的细节对比

4.2 Savitzky-Golay滤波数据处理

针对Savitzky-Golay 滤波最优参数的研究[9]，本文选取拟合阶次为4次拟合，分别选择窗宽(即为截取的数据个数)为5，9，11，15，27为滤波窗宽，对光谱信号进行拟合，窗宽即窗口中的数据点。经过多组数据处理，发现当滤波窗宽为5时，信号去除噪声的效果并不明显。随着滤波窗宽的增加，去噪效果增加，但是如果滤波窗宽过大会导致许多特征吸收峰减少。滤波窗宽为27时发现许多特征信号被滤除。经过多组数据的处理，发现滤波窗宽选择11时能很好的拟合原始数据，完整的保存了信号的特征峰值。图5所示是窗宽选择为5，11，27时信号Savitzky-Golay 滤波去噪后的波形图，可以明显看到窗宽为11时滤波效果最好。

4.3 傅里叶变换滤波数据处理

通过对臭氧吸收曲线的实验数据与臭氧吸收截面的观察分析，发现在245～270 nm波段间有一些独立的吸收峰呈周期性变化。波峰与波峰之间的距离为0.3 nm，实验取25 nm为一个周期，设定频率即为波数。对这一波段的数据进行傅里叶变换，结果如图6所示。

经过多组数据的处理认为频率大于1的部分为高频噪声，对其进行滤除，剩下的数据进行逆傅里叶变换后得到去除噪声后的波形如图7所示。

通过观察图7发现，傅里叶变换去噪后得到的信号比较平滑，但与原始信号的相似性低，在245～250 nm波段明显可以观察到没有很好的拟合原始信号。从根本上分析，傅里叶变换只在频域范围内进行处理，直接截去高频系数的方法趋于单一，有些比重较小的有用信号可能被滤除掉。

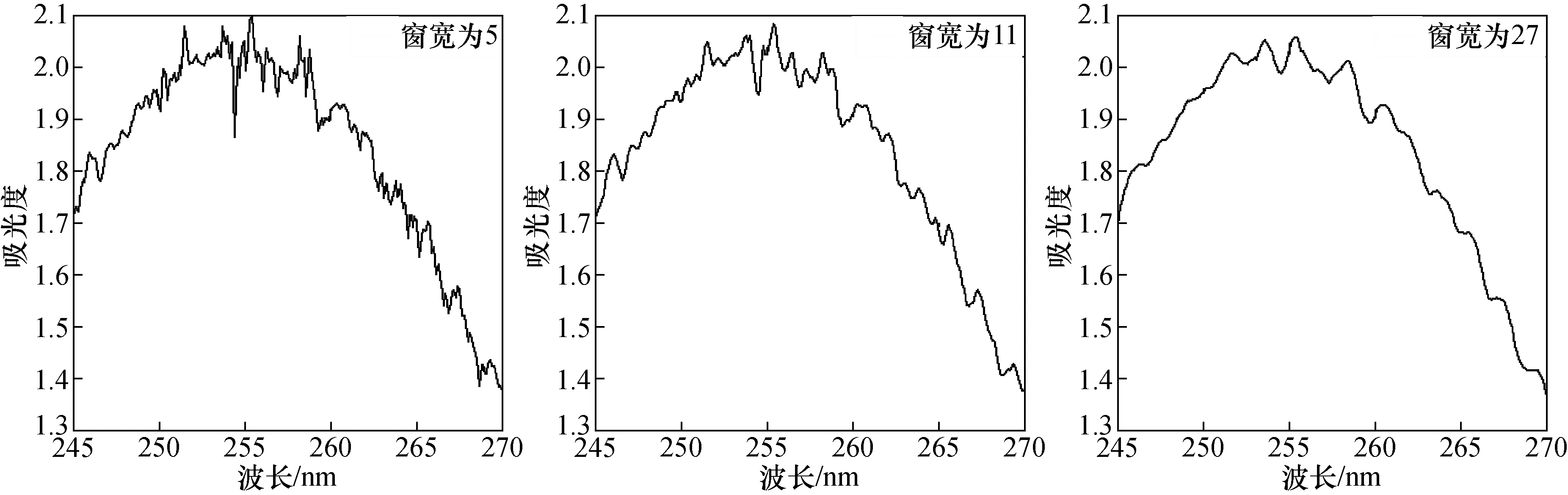
图5 窗宽为5、11、27时Savitzky-Golay 滤波后臭氧吸光度

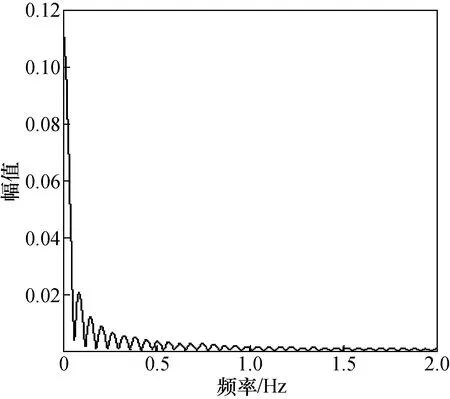
图6 傅里叶变换图

5 实验结果分析与评价

本文信噪比(SNR)定义为

SNR=10 log10(ps/pn)

(3)

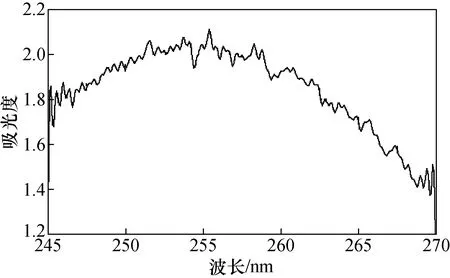
图7 傅里叶变换去噪后的臭氧吸光度

均方根误差(er)定义为

(4)

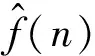
氮气流量为1 000 mL/min，氧气流量分别为 5 mL/min，10 mL/min，15 mL/min，20 mL/min，30 mL/min，40 mL/min的情况下，利用3种去噪方法分别求取信噪比与均方根误差。

表1为3种滤波方法的信噪比。研究发现：通入5 mL/min氧气时信噪比最低；随着氧气流量的增加，信噪比逐渐增大，在通入20 mL/min氧气附近时信噪比最大；随着通入氧气流量的再次增加，信噪比逐渐减小。说明通入氧气量在15 mL/min到30 mL/min时，测量较为准确。

对比这3种滤波方法的信噪比，可以发现：3种滤波方法均取得了良好的滤波效果。Savitzky-Golay滤波去噪效果最好，其次是小波去噪，只有傅里叶变换去噪相对来说较差，小波中wden函数的信噪比相对wdencmp函数更高。傅里叶变换滤波效果差，除了本身只能在频域范围内进行处理，分析其原因有以下两点：

(1)傅里叶变换适合滤除那些具有近似周期性的波动信号，通过观察臭氧的吸收曲线发现：臭氧在245～270 nm这个波段间的周期性吸收并不十分明显。

(2)虽然通过多组数据处理确定频率大于1 Hz的部分为高频噪声，但是仍然存在误差。

表2为3种滤波方法各自的均方根误差。在臭氧为低浓度的情况下，傅里叶变换去噪反而效果最好，这体现了信号在频域范围内进行处理的优势，信号较弱的情况下也能较为准确地滤除高频噪声。但从整体效果来看，小波变换去噪与Savitzky-Golay滤波去噪效果较好[12]。

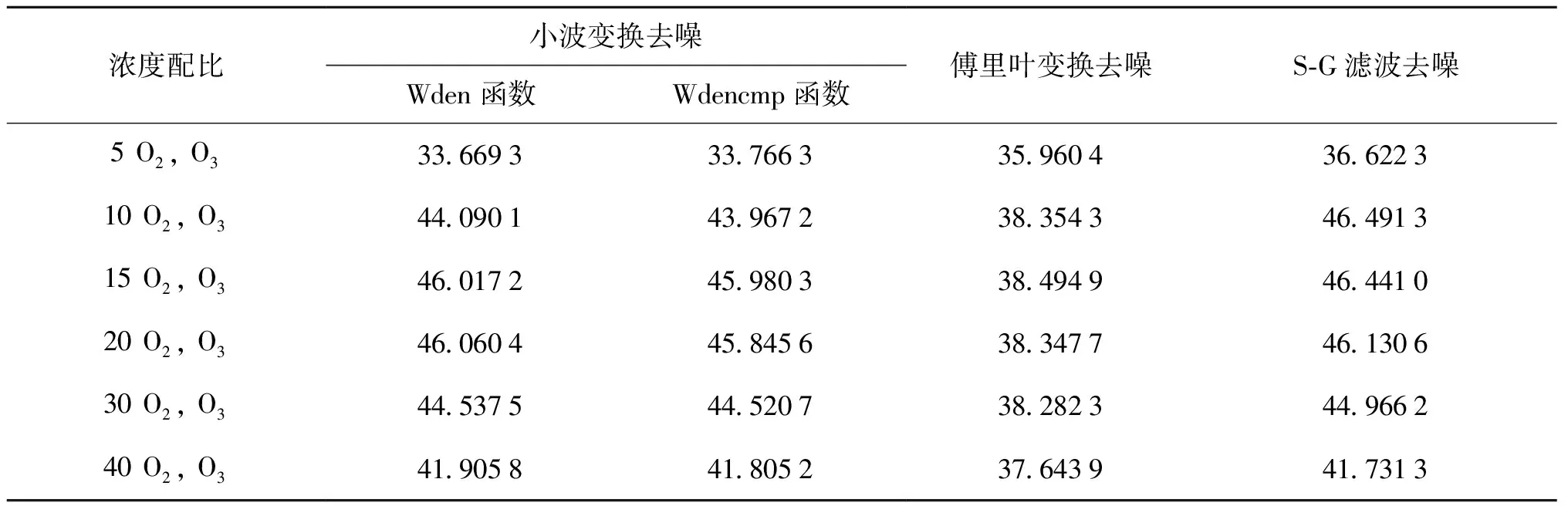
表1 3种去噪方法的信噪比

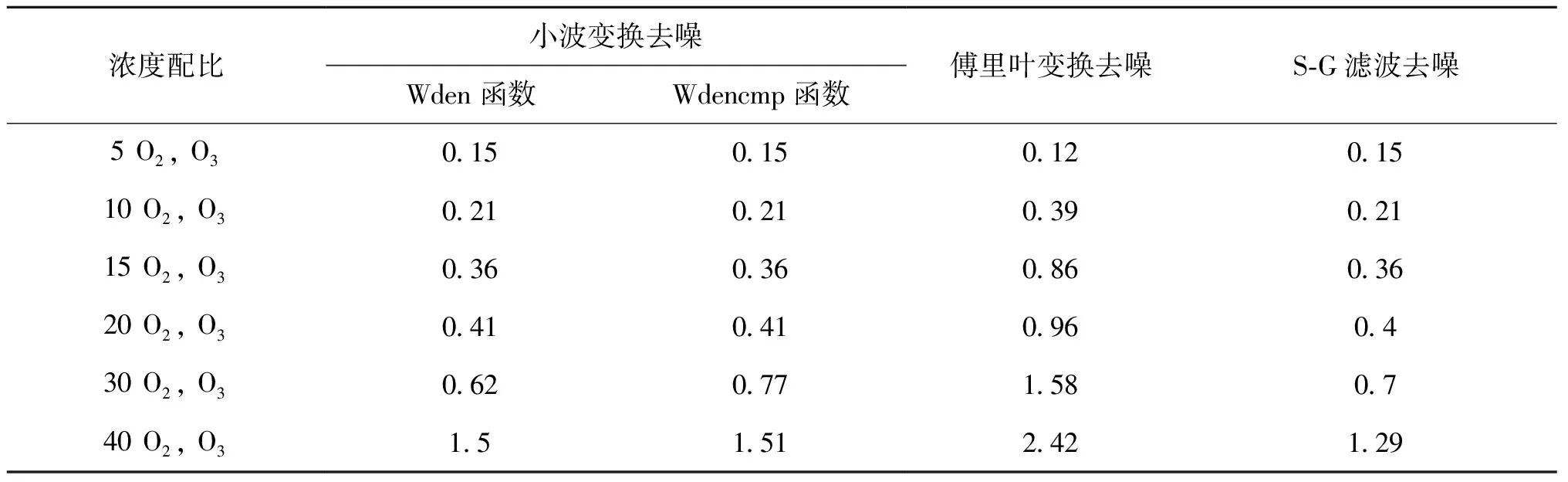
表2 3种去噪方法的均方根误差

小波变换与Savitzky-Golay滤波在信噪比与均方根误差方面均取得了不错的效果，为选取适合本系统最佳的滤波方法，比较了两者的细节图，如图8和9所示。

图8 wden函数小波变换细节图

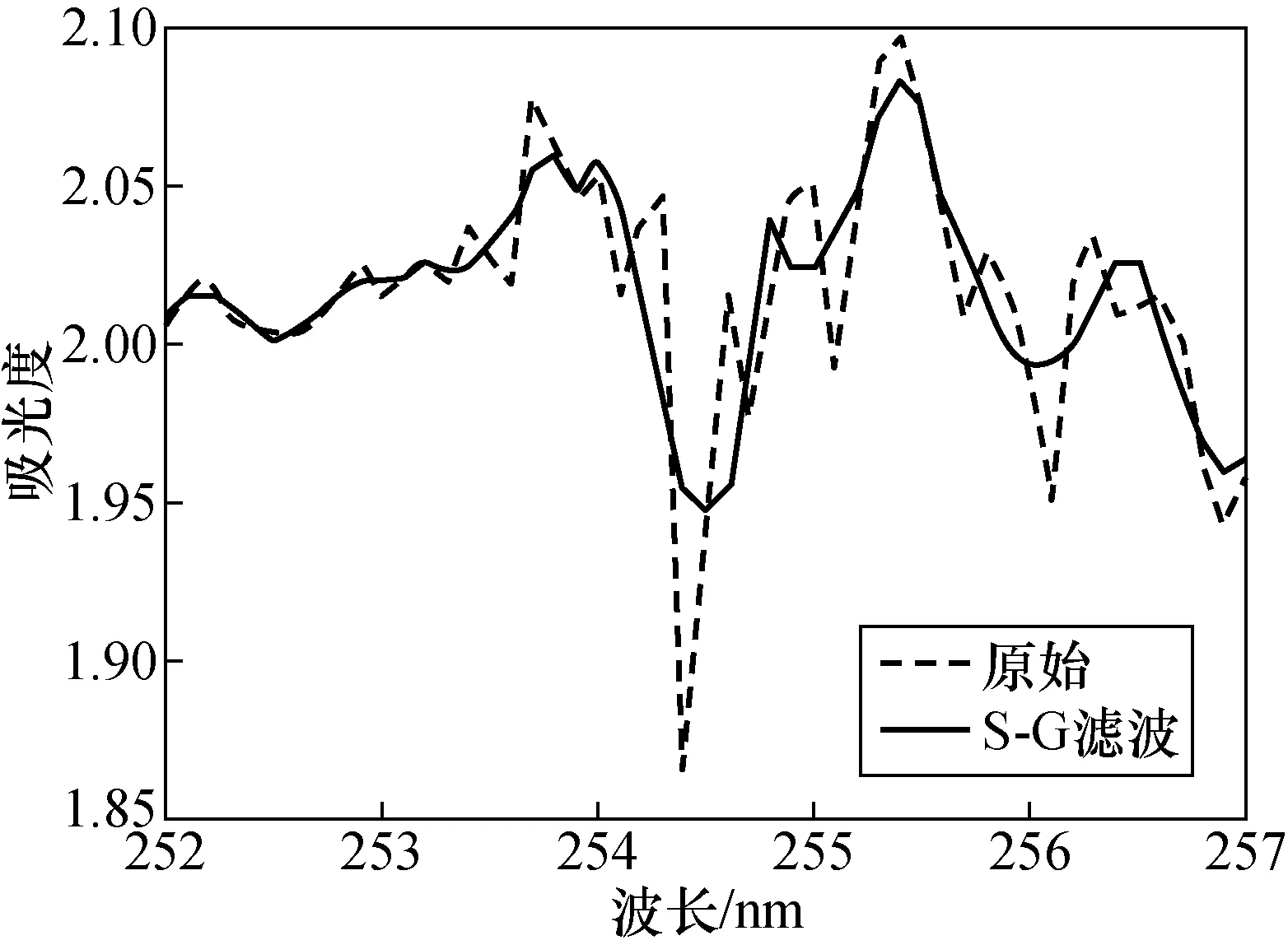
图9 Savitzky-Golay 滤波细节图

从两者的细节放大图中可以看出，Savitzky-Golay滤波不仅滤除了噪声，在细节方面更加凸显。综合来看在用DOAS技术监测臭氧浓度选择Savitzky-Golay滤波进行去噪处理精度更高。

6 结 论

基于臭氧吸收光谱的去噪声原理，本文选用了常用的小波变换、Savitzky-Golay滤波和傅里叶变换3种去噪方法。详细分析滤除噪声后的光谱图、信噪比和均方根误差，实验结果表明：傅里叶变换滤波效果较差，Savitzky-Golay滤波与小波变换相比具有更高的信噪比,更好地保存了信号的吸收特征，有效地去除了噪声，利于吸收光谱技术测量臭氧浓度的反演。Savitzky-Golay滤波在去噪方面有很好的适用性，可优先应用于臭氧的光谱计量分析。