基于烟花算法与长短时记忆网络的模温预测方法研究

张典范，栗子豪，程淑红

(1.燕山大学 车辆与能源学院，河北 秦皇岛 066004；2.燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

近年来，汽车轻量化的发展带动了低压铸造行业，低压铸造工艺中铸件液固成型温度场控制和利用计算机软件模拟分析模具关键部位的温度曲线是其核心[1，2]。模具温度在铸件成型过程中起着关键作用，以铸造生产中模具温度建立模型[3]，精准预测模温，可优化温度控制系统，提高铸件质量[4]，并可为铸造成型模温自动控制提供保障。

随着神经网络的出现，传统的大数据预测方法几乎均采用了BP神经网络[5～7]，其对模具温度预测模型的应用也较为广泛[8]，然而，BP模型更适合小规模的样本数据，难以寻找大规模数据中变量的变化规律，从而导致大规模数据预测准确度低。长短时记忆网络(long and short term memory network，LSTM)具有独特的记忆性能特点[9]，该模型在语义分割[10，11]、目标识别[12]、机器翻译[13]等领域应用前景广泛。

模具温度是低压铸造生产中影响铸件质量的一个重要指标，针对BP神经网络对模具温度预测准确度低的问题，本文结合铸造工艺生产方式和灰度关联分析方法(grey relation analysis，GRA)[14，15]，分析出影响模具温度关联度高的变量，建立了低压铸造模温预测的影响因子变量集合，采用烟花算法(fireworks algorithm，FWA)[16]优化LSTM模型的超参数，将建立的FWA-LSTM模型应用于模具温度预测建模中，并进行了仿真实验。

2 模具温度的影响因子变量选取

低压铸造中模具温度主要取决于合金液液固成型和冷却系统的冷却状况。在低压铸造铸件成型过程中，合金液进入模具型腔前，经过在保温炉中静置，并在压力的作用下，使合金液由下而上匀速压入铸件模具型腔中进行浇注，浇注完成后，通过冷却系统将模具中的热量传走，从而使合金液凝固形成铸件。初步确定模具温度的影响因子变量集合为：冷却水流量、冷却水温度、冷却时间、冷却管道与模具之间距离、冷却管道个数、合金液压力、挤压速度。采用GRA对影响模温因素的数据进行灰关联计算，达到降维的目的；将获得新的模温影响因子数据集作为预测模型的输入变量集合。

初始影响因子变量集合：

(1)

模具温度集合：

Y={Yj|j=1,2,…,M}

(2)

式中：X是初始变量集合；Y是模具温度集合；M是一组影响因素变量的数据量；N是初始变量的维度。

灰色关联系数为：

(3)

式中：ρ为分辨系数，0<ρ<1，如果ρ越大，则相关系数之间的差越小，辨别能力越强，通常ρ取0.5。

对各个影响因素分别计算其关联系数的均值，来反映各个影响因素与模具温度的关联关系，计算表达式为：

(4)

式中ξ代表灰色关联系数。

低压铸造模温的影响因子变量集合与模温关联度值见表1。

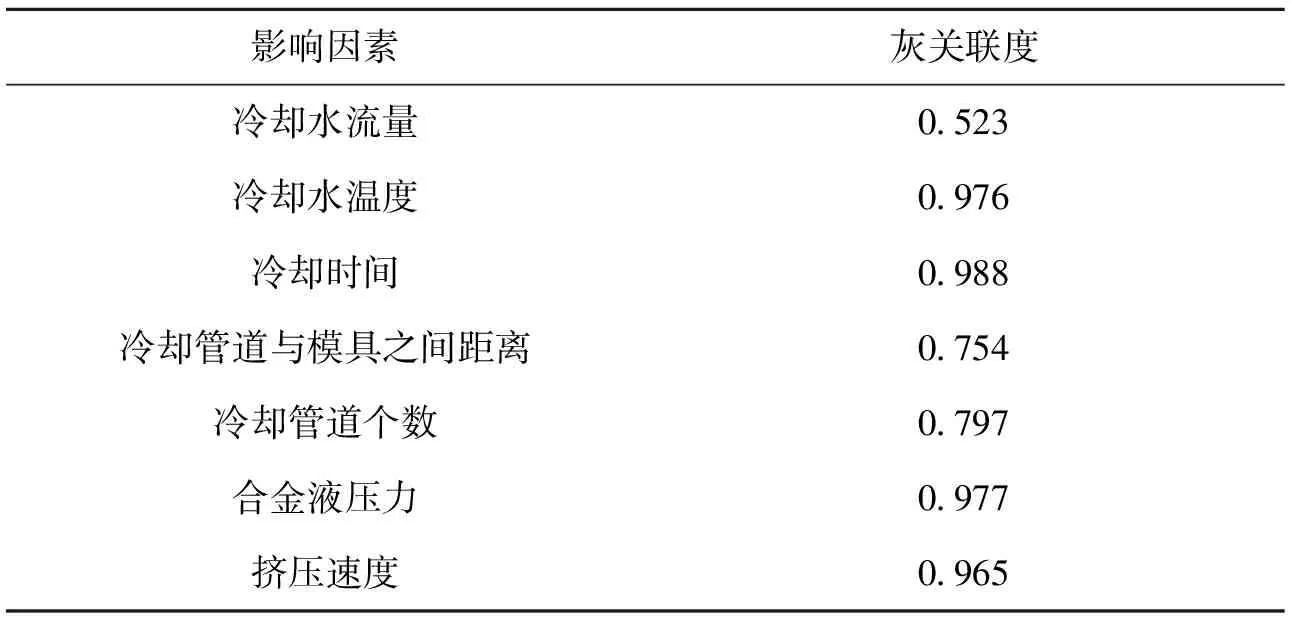
表1 低压铸造模温相关影响因子变量灰关联度

设定灰关联阈值为0.85，根据表1可获得模具温度预测模型的输入集合数据为：冷却水温度、冷却时间、合金液压力和挤压速度。预测输出变量为：模具温度。

3 基于FWA-LSTM预测模型

由于递归神经网络可以在传统的BP神经网络基础上，增加隐藏层中神经元之间的水平联系，所以递归神经网络的最重要特征是下一个时间序列的神经元可以获取前一个时间序列的神经元。因此，整个网络具有记忆功能，递归神经网络可以在模温影响因子数据集上学习时间序列的特征。然而，随着模温影响因子数据集的个数增加，递归神经网络易于发生梯度爆炸。针对这种现象采用LSTM模具温度预测模型，利用其特有的输入门、遗忘门、候选门和输出门结构的相互作用，提出FWA优化LSTM的超参数，来提高预测精度。

3.1 LSTM结构及算法

LSTM的内部结构中，重复的模块比单一的神经网络层复杂的多。如图1所示，每个神经元(图1中由3个神经元组成)中内部有4个以一种独特的方式进行连接，图中箭头的方向表示信息传递的方向，标号A表示神经元A，h(t-1)表示上一个神经元的输出，x(t)表示当前神经元的输出。图中正中间内部结构里的圆圈表示向量的逻辑门运算，矩阵形状表示学习到的神经网络层(由双曲正切函数tanh和σ表示函数Sigmoid组成)；LSTM关键在于神经元之间的主信息交互，主信息交互(穿过神经元的水平线)类似于传送带，主信息在每个神经元内部通过逻辑门运算进行处理，如此重复形成了循环结构。

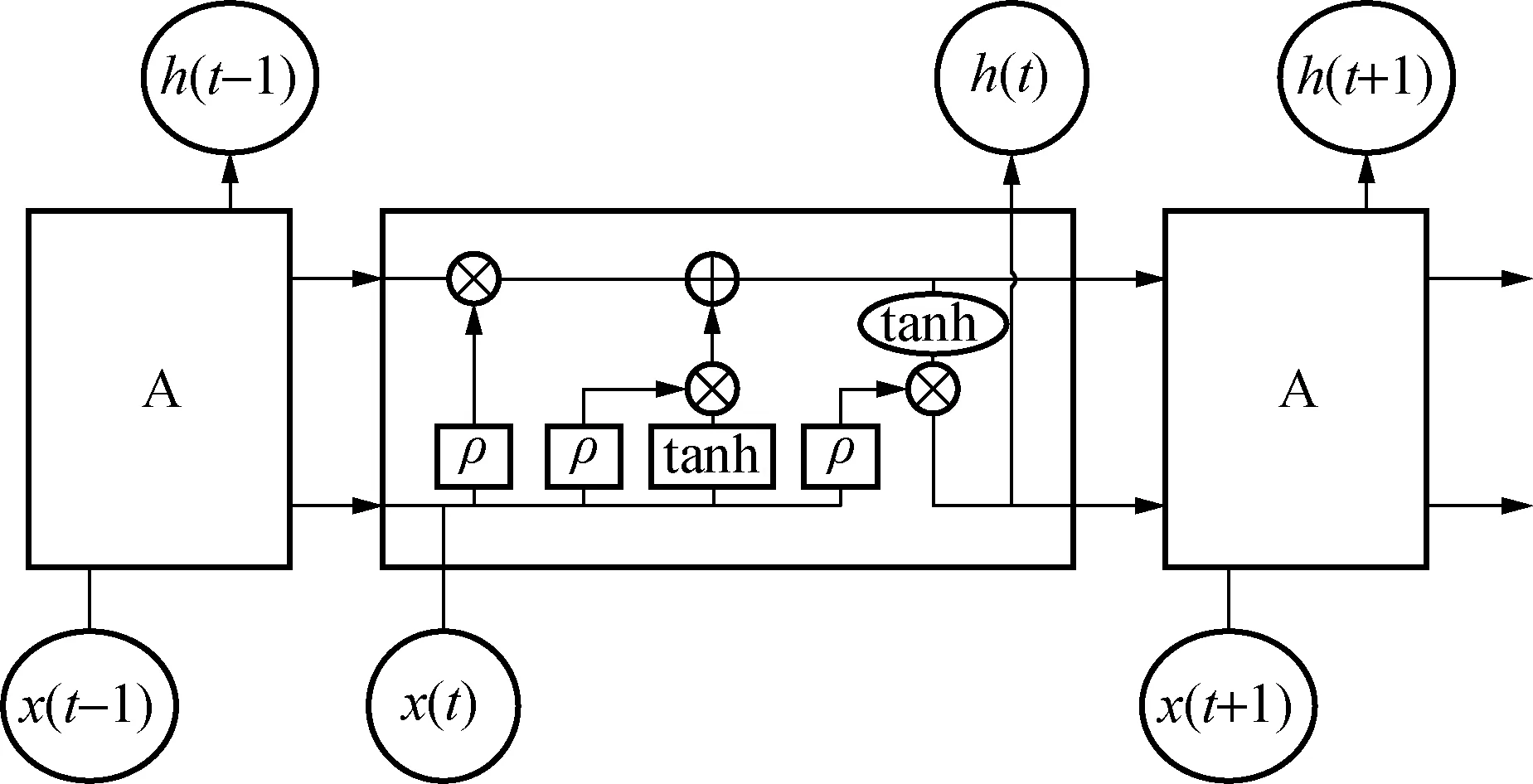
图1 LSTM的内部结构

信息在进入每个LSTM神经元内部后，第一步是通过遗忘门来控制是否遗忘上一次神经元的状态，通过激活函数Sigmoid，得到输出f(t)，计算表达式为：

f(t)=σ(Wf×h(t-1)+Uf×x(t)+bf)

(5)

式中：Wf，Uf，bf为线性关系的系数和偏倚；σ为Sigmoid激活函数。

第二步控制哪些信息通过输入门。输入门由两部分组成，该层的第一部分Sigmiod层控制更新哪些信息；第二部分为双曲正切函数tanh层候选更新生产的向量。见式(6)和式(7)：

i(t)=σ(Wi×h(t-1)+Ui×x(t)+bi)

(6)

a(t)=tanh(Wa×h(t-1)+Ua×x(t)+ba)

(7)

式中：Wi,Wa,Ui,Ua,bi,ba为线性关系的系数和偏倚。

结合遗忘门和输入门所得结果作用到隐藏神经元状态C(t)，数学表达式为：

C(t)=C(t-1)⊙f(t)+i(t)⊙a(t)

(8)

式中⊙为Hadamard积。

第三步控制是否通过输出门输出隐藏状态h(t)。该输出门也由两部分组成，第一部分是前一个序列的隐藏状态h(t-1)以及本序列数据x(t)和激活函数Sigmoid；第二部分由隐藏状态C(t)和双曲正切函数tanh。见式(9)和式(10)：

o(t)=σ(Wo×h(t-1)+Uo×x(t)+bo)

(9)

H(t)=o(t)⊙tanhC(t)

(10)

式中：Wo，Uo，bo为线性关系的系数和偏倚。

通过上述步骤，LSTM进行前向传播算法，不断迭代更新遗忘门输出，输入门输出和输出门输出。

3.2 烟花算法建立

针对长短时记忆网络误差梯度下降算法全局寻优能力差，寻优准确度低等问题，提出采用烟花算法(FWA)对LSTM的参数进行优化。采用烟花爆炸的搜索机理发现更优解，提升算法的全局寻优能力，增加了搜索的准确度。在FWA算法中[17]，假设有n个参数组合，其中Xi=x1,x2,…,xd是解空间中的1个解，根据适应度函数f(Xi)计算每个烟花的适应度值，计算适应度值获得的火花个数Si为：

(11)

ymax=max(f(Xi))，i=1,2,…,n

(12)

式中：m是控制n个烟花产生火花总数的参数；ξ是接近0的小数；f(Xi)代表适应度函数。

为了避免绚丽烟花的影响，定义参数组火花的数量Si，如式：

(13)

式中：a，b是常量。

与设计的火花数相比，良好的烟花爆炸产生的火花数也接近爆炸中心，良好的烟花爆炸能量低于不良的烟花爆炸能量。爆炸位移范围定义幅度Ai：

(14)

ymin=min(f(Xi))，i=1,2,…,n

(15)

式中A是预设的最大振幅。

根据爆炸效果，在烟花算法中，应使用更多的火花来搜索烟火周围的局部区域，并且爆炸效果不良的烟火的最佳位置可能远离烟火的位置，从而使搜索半径变大；爆炸效果好的烟花比爆炸效果差的烟花产生更多的火花，爆炸幅度小。图2为2种不同的烟花爆炸效果。

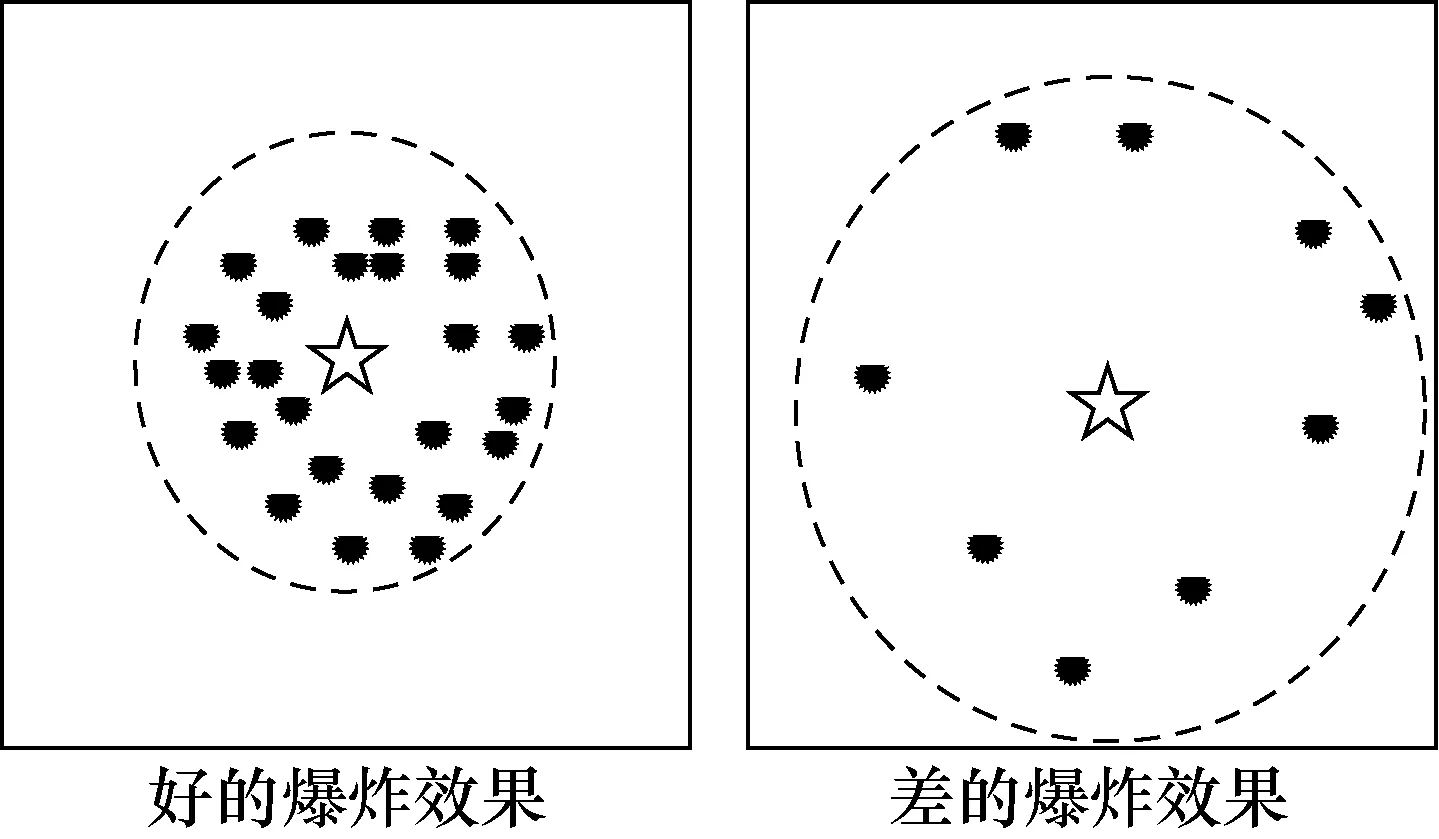
图2 烟花算法爆炸效果

Xi被选择进行下一次迭代的概率为：

(16)

式中R(Xi)代表当前个体到集合M的距离。

3.3 FWA优化LSTM参数

LSTM的参数和结构选取直接影响模型的预测精度，采用FWA优化LSTM预测模型参数比传统的神经网络训练速度快，并且避免模型参数选取的不科学性，对模型结构参数的优化能更好地提高预测精度。根据FWA优化LSTM模型的3个参数，分别为时间窗口大小，批处理大小和隐藏层单元的个数。以模具温度预测模型当中训练数据集的平均绝对“%”误差作为FWA中的适应度函数，其表达式为：

(17)

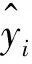
原始数据经过GRA处理后作为模温训练模型的输入数据进行训练，图3为FWA-LSTM和LSTM算法的模温偏差值随迭代次数变化的曲线，损失函数均选择平法差损失函数。由图中可以看出：LSTM收敛速度慢，模温预测精度较低；采用FWA优化LSTM算法收敛速度更快，模温预测误差较小。从而证明了FWA全局寻优能力强。

FWA-LSTM模温预测模型的流程为：

1)将低压铸造生产线上的数据分为训练数据和验证数据。

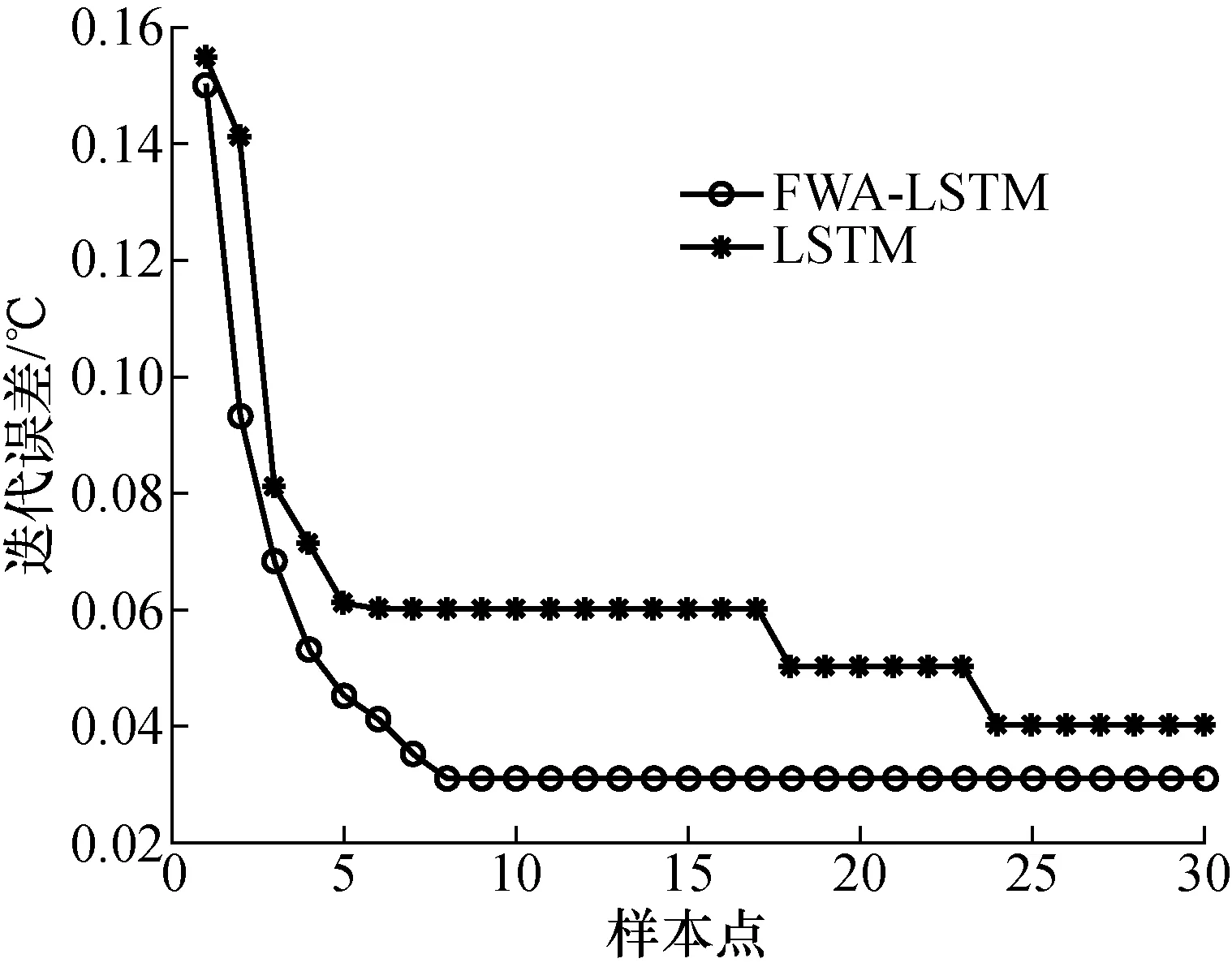
图3 对比FWA-LSTM与LSTM迭代误差图

2)初始化FWA的参数，初始烟花数量n，烟花种群大小M,预设的最大振幅A，常量a，b。

3)将FWA-LSTM模型的3个参数，时间窗口大小范围[1,15]，批处理大小范围[1,50]和隐藏层单元的个数范围[10,20]作为优化对象。

4)通过爆炸算子生产火花，计算烟花的适应度值，并进行训练数据进行训练。

5)根据烟花适应度值和烟花爆炸的效果，判断烟花群体是否进行迭代更新。

6)判断满足终止条件，若满足终止条件则输出最优参数值，否则返回第3步。

7)利用最优参数构建FWA-LSTM模具温度模型。

4 实验研究

从某低压铸造生产线数据采集存储系统中获取样本数据600组，结合生成工艺，顺序选取560组数据作为训练数据，下一段时刻剩下的40组数据进行预测数据。部分原始数据见表2。

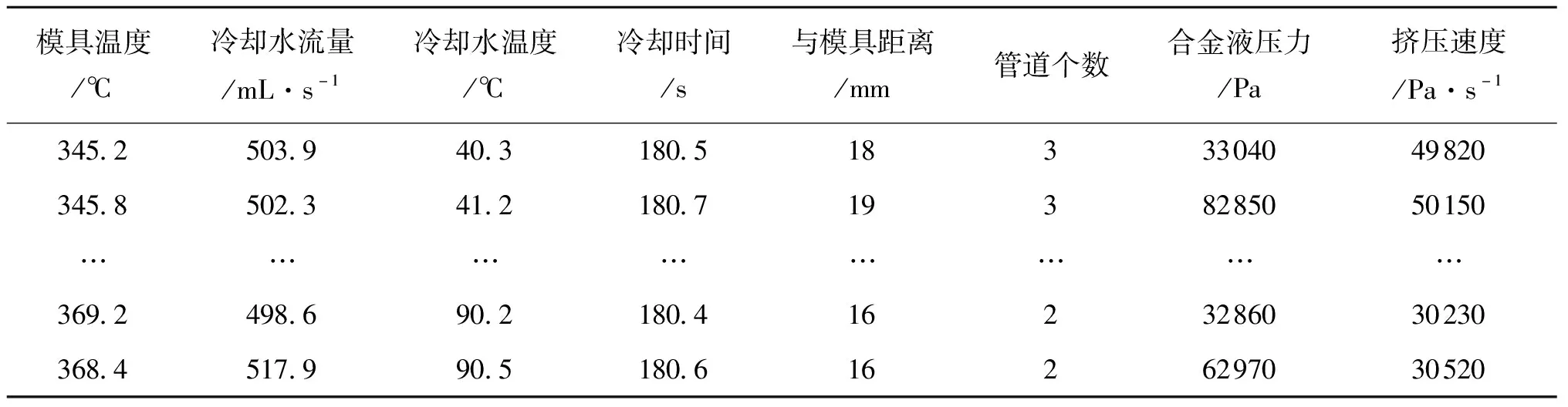
表2 部分原始数据

为了充分验证原始数据经过GRA处理是否会降低网络的预测能力和FWA-LSTM模温预测算法的有效性，分别将原始数据经过GRA处理和未经过GRA处理后的数据作为模温预测模型的输入数据进行预测。采用BP神经算法、LSTM算法和FWA-LSTM算法进行比较，烟花算法中，初始烟花数量n=5，烟花种群大小M=50，预设最大振幅A=40，常量a=0.04，b=0.8，最大迭代次数设为100。获得的FWA-LSTM模温预测模型的最优超参数：时间窗口大小为10，批处理大小为50，隐藏层单元个数为12。经过仿真实验测得以原始数据经过GRA处理和未经过GRA处理的3种方法的预测模具温度结果见图4所示。

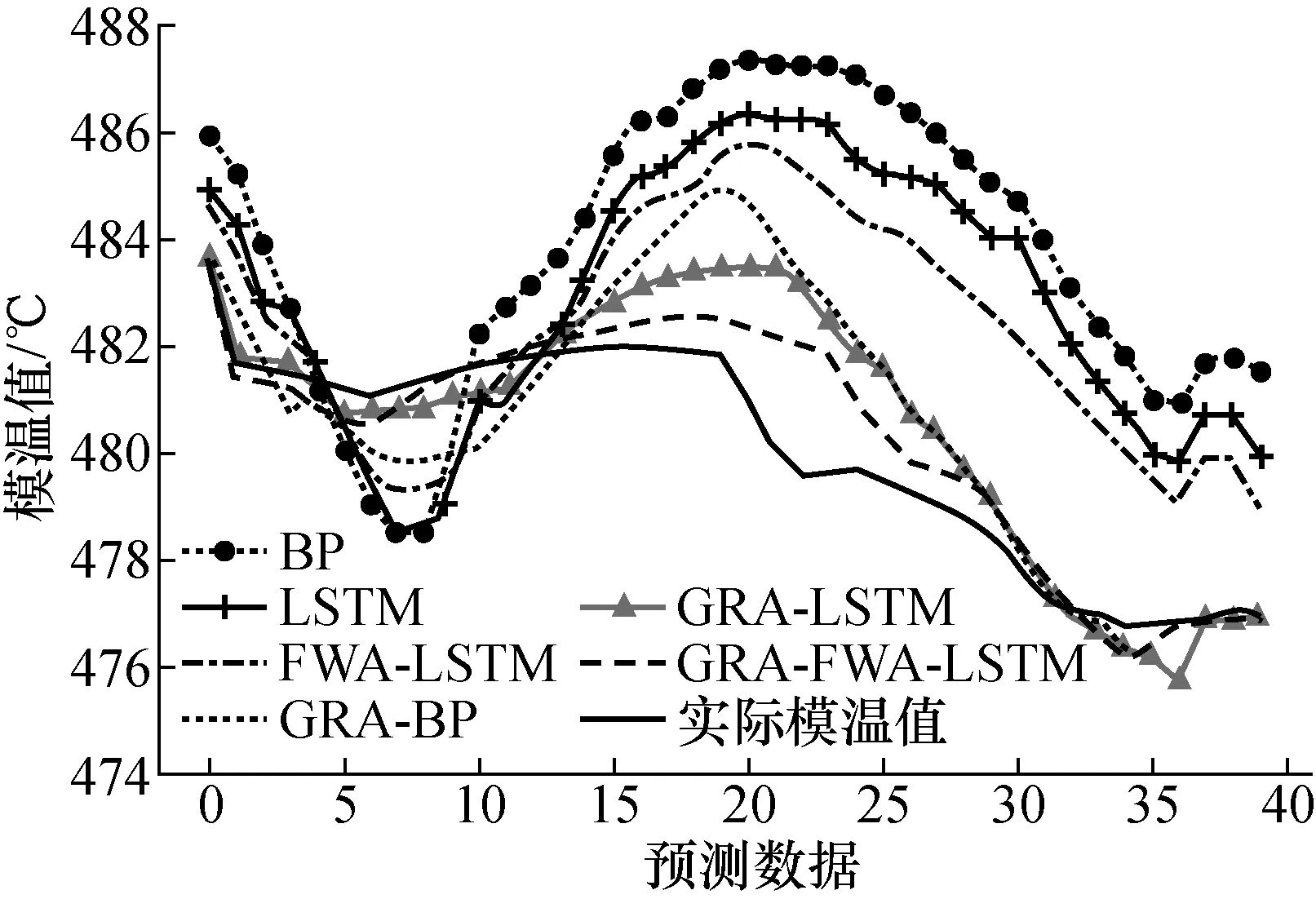
图4 3种方法预测结果图

整个实验过程采用平均绝对百分比误差MAPE和绝对误差ε两个指标作为衡量模型预测精度的标准，结果见图5和表3所示。

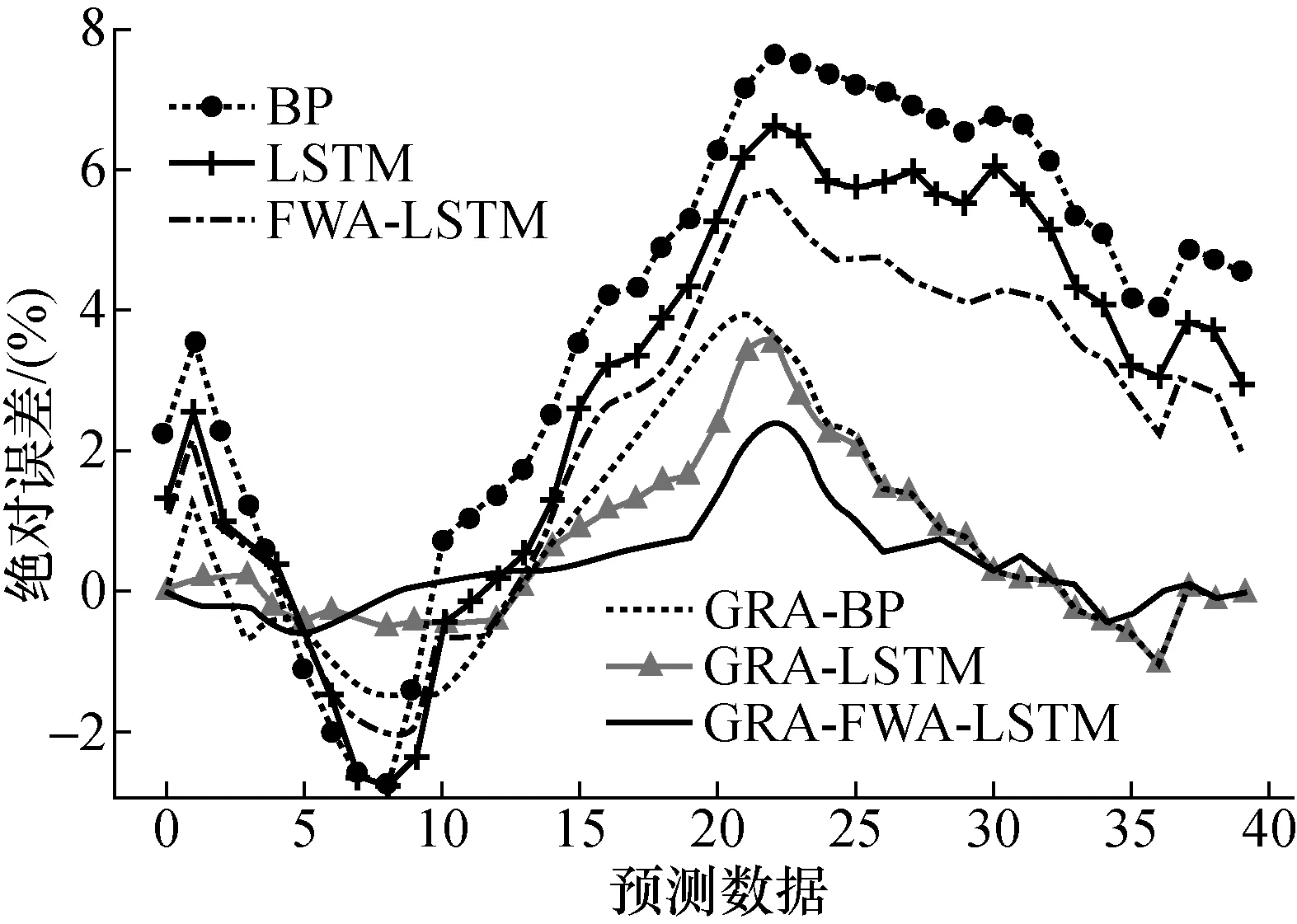
图5 3种方法预测绝对误差图

其中，MAPE和ε的计算表达式分别为：

(18)

(19)

由图4和图5所示的模温预测结果可得，原始数据经过GRA筛选处理后的模型预测精度有所提升，并不会降低网络的预测精度，当原始数据经过GRA处理后，相比于BP神经网络预测算法、LSTM预测算法，采用FWA-LSTM预测算法得到的模温预测值更加准确，具有更好的实验效果。

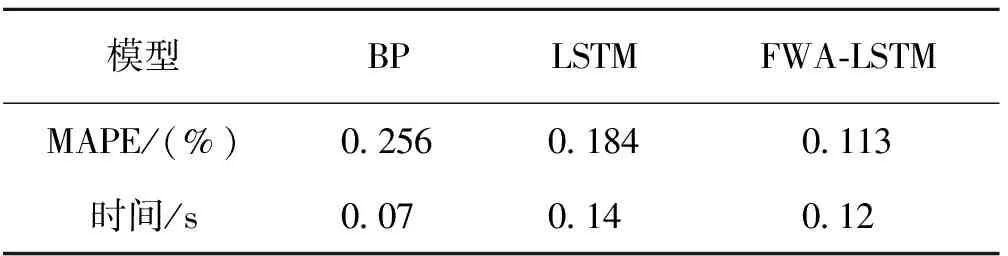
表3 经GRA处理后各方法泛化能力比较

由表3所示，BP神经网络的结构简单，因此运算时间最短，但BP算法的预测效果相对较差；LSTM预测算法和FWA-LSTM预测算法计算时间相差很小，并且FWA-LSTM预测算法平均绝对误差更低。从而，证明基于FWA-LSTM的低压铸造模温预测模型预测绝对误差小于2.4 ℃，平均绝对百分比误差小于0.12，泛化能力更强。

5 结 论

本文提出了基于FWA-LSTM的模温预测方法，通过低压铸造生产工艺和GRA的结合，得出模温预测影响因素的集合，降低了预测模型的输入维度，推导了FWA-LSTM建模算法，并根据实际数据进行训练和验证。实验结果表明，基于FWA-LSTM的模温预测模型精度更高。准确的预测铸造模具温度，不仅可以使操作人员根据模具温度调节铸造工艺生产参数，同时也为低压铸造自动控制提供基础，从而达到提高铸造生产效率和降低生产能耗有重要的指导作用。