偏度约束的负半熵-下半方差投资组合研究

欧 攀,王 沁,段静静,周文浩

(西南交通大学 数学学院，四川 成都 611756)

现代投资理论的核心是投资组合理论。1952年，MARKOWITZ提出的均值方差模型,开创了投资组合量化风险的先例。在均值方差模型中，假设资产组合收益率服从正态分布，用二阶中心矩(方差)作为风险度量指标、一阶矩(期望)作为收益度量指标，研究在一定风险水平上取得最大的预期收益或在一定收益水平上使风险达到最小的投资组合选择问题。

近年来，越来越多的学者关注资产组合研究。如王延章等[1]考虑投资者在实际投资时更关心资产收益低于预期收益的那部分风险，因此将下半方差模型应用于债券投资；郑伟[2]指出收益分布并非对称的正态分布；艾克凤[3]研究指出资产的收益率服从非对称的厚尾分布；DITTMAR[4]的研究表明投资者在做出投资组合选择时考虑资产或资产组合收益率高阶矩的情况，在期望和方差相同的情况下绝大多数投资者偏爱具有较大的三阶中心矩的收益率；BRITO等[5]在半方差度量风险的基础上引入三阶矩偏度系数；王波等[6]考虑用CVaR代替方差度量资产风险，建立投资组合模型，并选取沪市和深市的8支股票进行实证分析。而后大量学者从信息熵的角度去度量风险，如徐湘[7]建立了可做空的Tsallis广义熵投资决策模型；RAO等[8]给出累积熵投资组合模型；张鹏等[9]给出了熵约束的投资组合模型；朱业春等[10]给出了熵补偿的Black-Litterman投资组合模型；宋燕玲等[11]给出了带偏度约束的正弦熵投资组合模型。

笔者考虑从收益率下跌风险的角度，用负半熵和半方差共同量化下跌的信息，引入偏度量化高阶矩风险，从而构建负半熵-下半方差-偏度投资组合模型，并给出了模型的隐式解，以期为投资者进行资产配置、资产选择和风险预测时提供一定的指导。

1 模型的构建与推导

1.1 建立模型

假设n种风险资产之间相互独立，以收益率的均值来刻画收益，以收益率的下半方差和负半熵量化风险，既考虑了未来收益率的随机不确定性，又兼顾了股市涨跌信息隐形的不对称性，使风险测度指标更加全面、精确和合理。偏度是衡量各个可能的收益率对期望值偏离的大小，偏度通常越大越好(一般大于0即可)。研究目标是最大化收益的同时最小化风险，故构建下半方差和负半熵尽量小、偏度尽量大的目标函数以使风险尽可能小，同时构建组合资产的期望收益率尽量大的目标函数以使收益尽可能大。建立的多目标投资组合优化模型为：

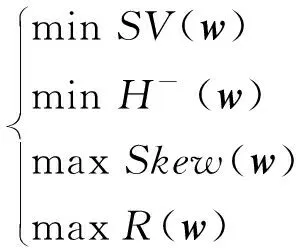
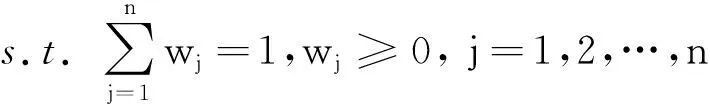
(1)

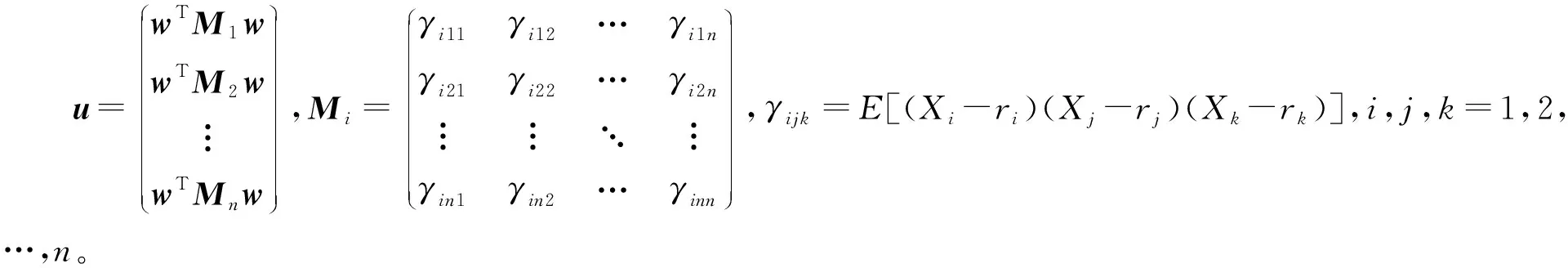
1.2 模型的推导

对于多目标组合投资模型，基于文献[12]的线性解法，将量化组合资产收益低于预期收益的那部分风险的下半方差与负半熵作为目标函数，将组合资产的偏度与收益放于约束条件中，从而转化为负半熵-下半方差-偏度的单目标模型(negative half entropy lower semi-variance skewness portfolio model，简称NE-SV-SK模型)：

minSV(w)+φH-(w)

(2)

其中,φ为调节参数,需满足φ≥0。

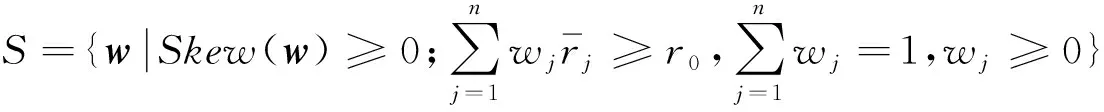
(3)

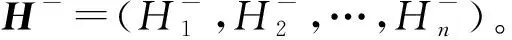
(4)

求解式(4)可得最优解w*的隐式解：

(5)

2 实证分析

2.1 数据描述

表1 泸深300的特征值和贡献率

从表1可以看出，前十个特征值的累计方差贡献率已达60%，因此考虑通过前十个特征值产生的载荷矩阵来挑选18只股票，以此代表泸深300指数的股票信息，所选股票信息如表2所示。

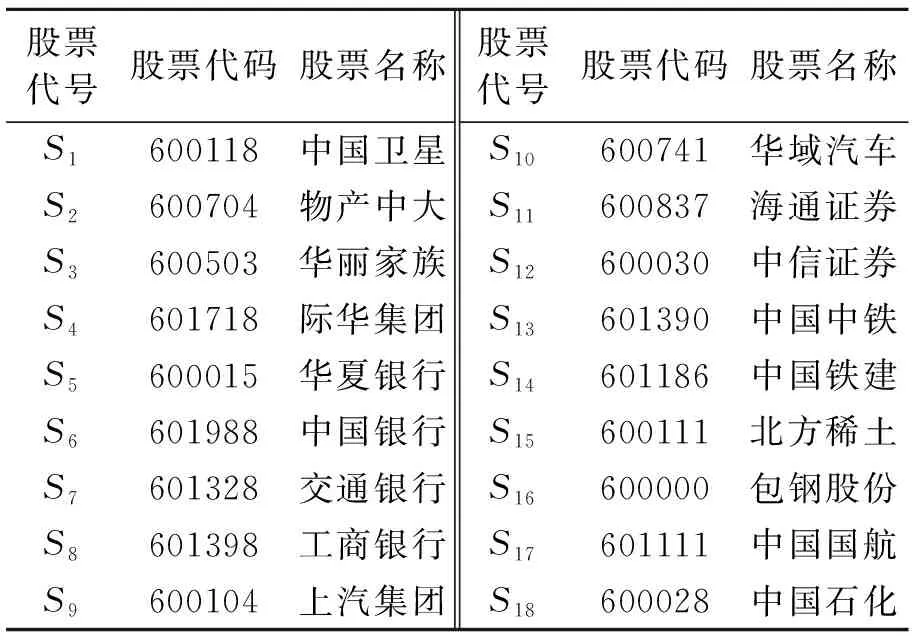
表2 挑选的18只股票信息

应用矩估计计算出各只股票的样本均值、样本方差、下半方差、负半熵、样本偏度，结果如表3所示。从表3可以看出：①在18只股票中，股票S2、S3、S10的下半方差比其方差要小得多，可见下半方差在方差中并非是对称的，下半方差能更加准确地度量股票收益向下波动的那部分风险；②18只股票中负半熵最小的是S5，而其下半方差和方差却比很多其他股票要大，并且对比18只股票的负半熵与下半方差可知，两者并没有呈现出相同的增减趋势，这说明虽然负半熵和下半方差均是度量低于期望收益风险的，但两者度量资产风险的角度不同。

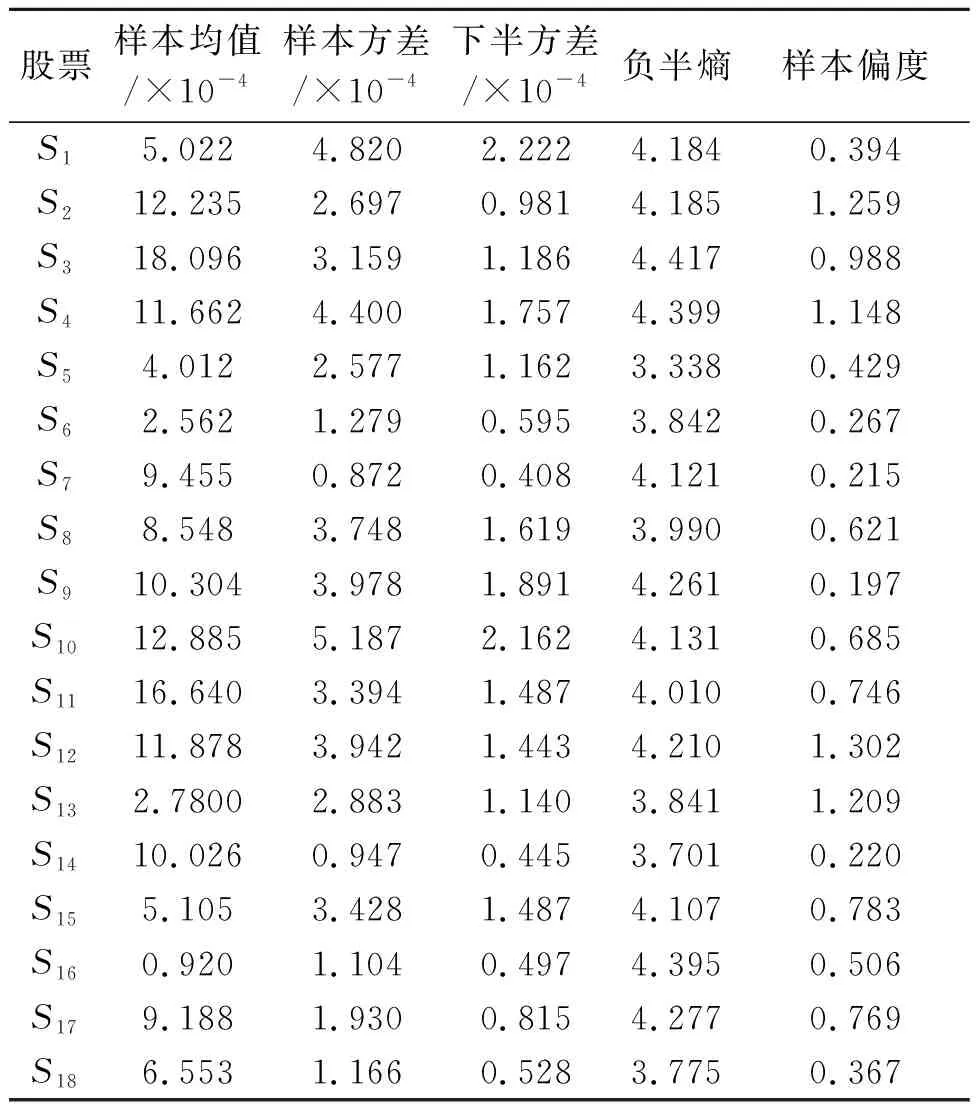
表3 各只股票的样本均值、下半方差与负半熵、样本偏度

2.2 模型实证分析

根据拉格朗日乘数法和梯度下降法对模型进行编程求解，模型中存在调节参数φ和收益参数λ，给出了相同收益参数、不同调节参数下18只股票的投资组合情况，如表4所示。

从表4可以看出：①模型求解的投资权重分布在第3、6、7、14、16、18只股票，没有呈现集中分布现象，符合分散投资理念。②随着调节参数的逐渐增大，负半熵的作用逐渐显现，使得股票S3、S6的投资权重呈下降趋势，股票S7的投资权重呈上升趋势。这表明用负半熵衡量风险时，股票S3、S6被度量出了更多的负半熵风险，股票S7被度量出了更少的负半熵风险。③随着调节参数φ的逐渐增大，下半方差呈增大趋势，负半熵呈减小趋势，这与负半熵在目标函数中比例变大相吻合。同时，不同的调节参数意味对熵度量风险的侧重不同，从偏度指标中可以看出在调节参数取0.000 02时偏度处于极大值，此时模型较佳。

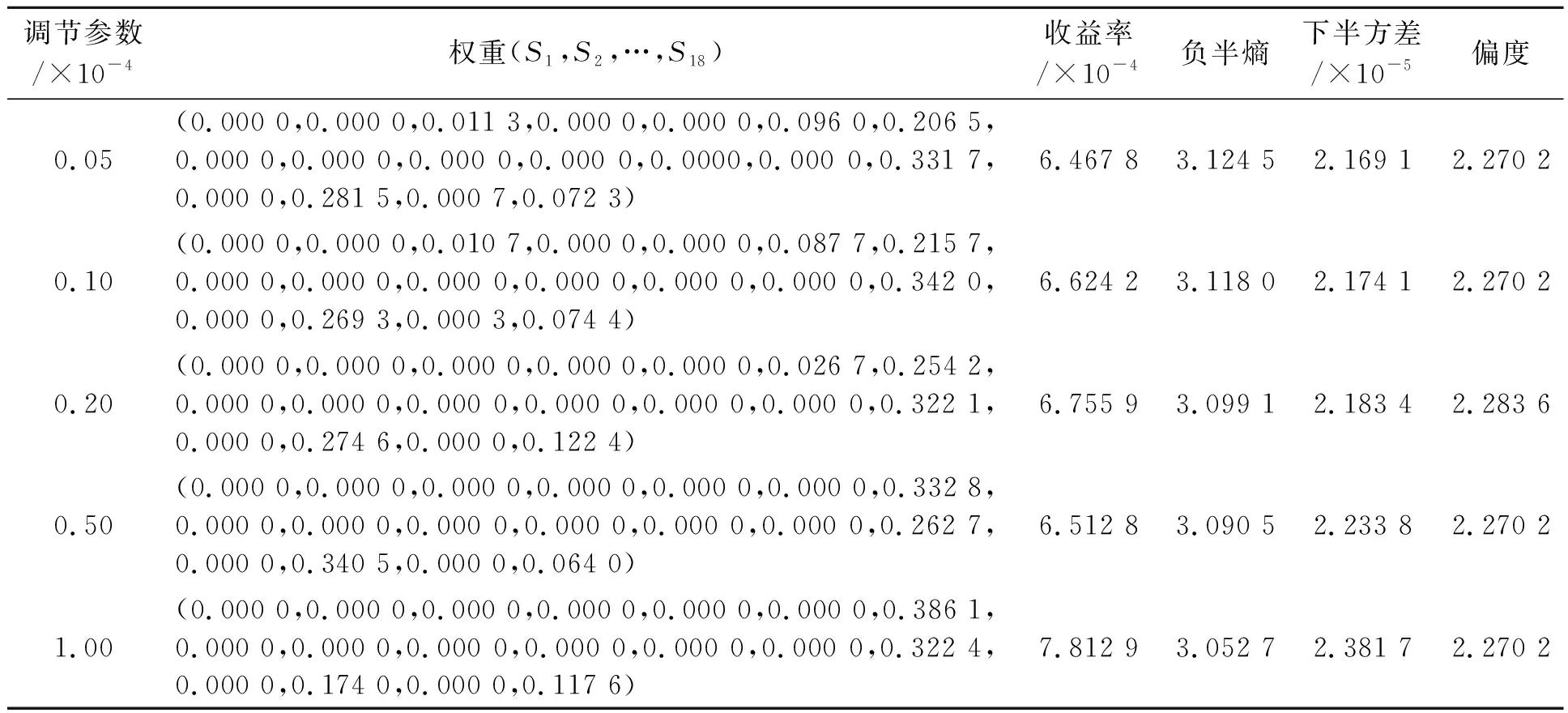
表4 不同调节参数下的资产组合情况(r0=0.000 3)

相同调节参数、不同收益参数下18只股票的投资组合情况如表5所示。

从表5可以看出：①随着收益参数r0的增大，呈现股票S3、S7、S18替代股票S6、S16的现象，可见股票S3、S7和S18发生超额收益的可能性更大。②在固定调节参数φ的条件下，随着收益参数r0的增大，负半熵与下半方差都呈现增大的趋势，这与收益更大、风险更大相吻合。③收益参数与调节参数为模型预设参数，分别表示资产组合的最小收益和负半熵的权重比例，不同投资者对收益和负半熵风险偏好的要求不同，收益参数和调节参数可根据实际情况进行调整。

2.3 模型对比

为进一步说明NE-SV-SK模型中负半熵和偏度对投资组合的影响，令NE-SV-SK模型中参数φ=0.000 02，r0=0.000 3，并与经典马科维茨模型(MV)、半方差模型(SV-SK)进行比较，具体结果如表6所示。

从表6可以看出：①与SV-SK模型相比，NE-SV-SK模型中股票S3、S6、S16、S17的权重比例有所减小，股票S7、S14、S18的权重比例有所增加，这可能是负半熵度量出了股票S3、S6、S16、S17更多的负半熵风险导致的结果；②在股票S16、S18上的权重比例存在显著变化，投资者在进行选股时应给予更多理性考虑；③观察收益率、下半方差、负半熵、偏度指标，NE-SV-SK模型比MV模型、SV-SK模型的收益更大，风险度量指标中下半方差和负半熵均更小，且组合资产偏度也存在明显提升。可见NE-SV-SK模型更能反映组合资产所面临的风险，能更有效地规避风险，为投资者在配置资产时提供更加合理的选择。

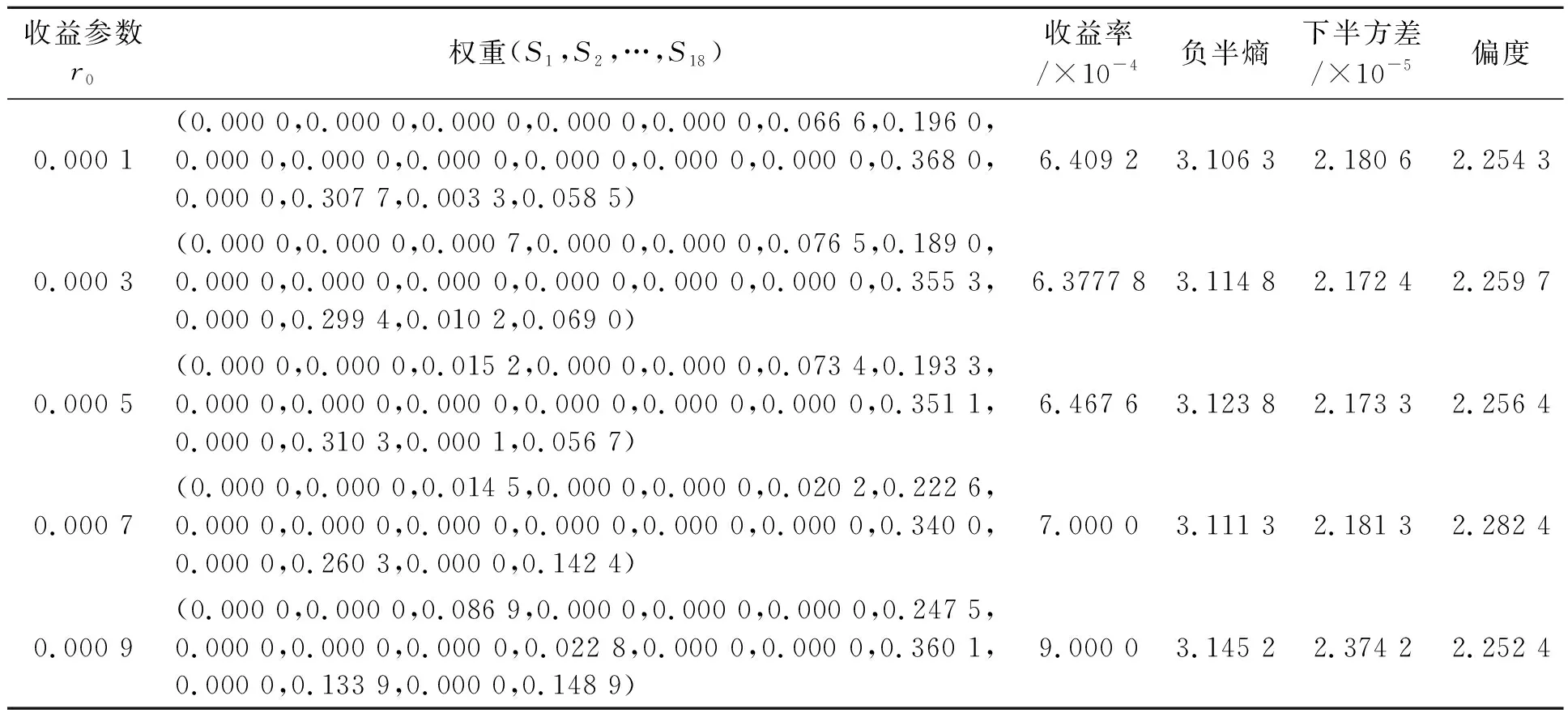
表5 NE-SV-SK模型在不同收益参数下的资产组合情况(φ=0.000 02)

表6 模型结果比较

3 结论

考虑到投资者更关心资产收益能否达到预期收益的心理，通过用负半熵补偿下半方差衡量资产收益低于预期收益的风险，并在约束条件中引入偏度系数，构建了NE-SV-SK模型。并选取18只股票进行实证分析，发现NE-SV-SK模型能获得更大的收益，更好地规避风险，并且发生超额收益的可能性更大。在投资者进行组合投资时，NE-SV-SK模型能给予投资者更多理性参考，对股票选择和风险预测也具有一定的指导意义。