考虑风险规避和渠道偏好的供应链定价研究
2020-06-13徐章一
周 珺,徐章一
(武汉理工大学 物流工程学院,湖北 武汉 430063)
在互联网+和电子商务快速发展的背景下,很多企业倾向于网上直销和传统零售渠道相结合的双渠道模式。但随着产品更新换代升级,废旧产品数量逐渐增加,企业也逐渐意识到实施闭环供应链的重要性。然而,这种模式的运行可能会加剧渠道冲突,也会导致供应链成员间风险规避行为有所增加。近年来,关于闭环供应链的研究主要集中在回收渠道选择、产品定价和供应链协调等方面。如GIOVANNI等[1]研究了由一个制造商和一个零售商组成的二级闭环供应链下制造商的回收模式选择。解凤珏等[2]考虑消费者对新旧产品的支付意愿,比较分析不同回收渠道下的最优决策,研究表明不同回收商的回收努力和能力影响再制造的定价决策。王悦等[3]建立了3种回收模式下的决策模型,指出当第三方回收商无利可图时,零售商回收模式可使供应链整体利润达到最大。陈艳等[4-5]分别通过设计最优风险分担契约、收益共享-成本分担契约实现闭环供应链总收益的最大化。以上文献都是针对传统零售渠道情形,且需求函数为线性需求。少数文献从定价与协调的角度对双渠道闭环供应链进行了研究,但是没有同时考虑风险规避和消费者渠道偏好两个因素。如赵静等[6-7]分别从渠道偏好和风险规避程度探讨不同回收模式下的双渠道闭环供应链运作策略。对于风险规避行为的研究,许民利等[8-9]基于CVaR分析集中和分散决策下的供应链决策问题。王道平等[10]研究供应链成员均为风险规避且生产信息不对称时的定价问题,结果表明风险规避型制造商获利更高。但大多数研究只考虑了单方风险规避行为对决策的影响,且供应链所处的环境不是双渠道闭环供应链,也没有涉及消费者偏好这一影响因素。
综上,目前在双渠道闭环供应链中同时考虑消费者偏好和风险规避的研究较少。因此,笔者构建一个制造商双渠道为主导、零售商为跟随者的闭环供应链,其中零售商负责回收废旧产品。结合消费者效用最大化,分别分析制造商和零售商均为风险中性、风险规避、单方风险规避3种情形下的最优定价决策,并通过数值模拟分析风险规避度、消费者偏好系数对供应链成员定价决策的影响。
1 问题描述及模型假设
1.1 问题描述

图1 双渠道闭环供应链系统结构
在信息对称的情况下,制造商为主导的二级双渠道闭环供应链的系统结构如图1所示。制造商不仅以批发价格W将产品卖给零售商,还以直销价格Pd直接将产品销售给消费者。零售商则将产品以零售价格Pr卖给消费者。零售商对废旧产品的单位回收价格为Pc,并以转移费用b卖给制造商,制造商对废旧产品进行再生产。
1.2 模型假设与符号说明
假设1新产品的单位生产成本为Cm,再制品的单位生产成本为Cr,Cm>Cr,用Δ=Cm-Cr表示生产再制品可节约的单位生产成本。为保证供应链成员均有利可图,假设Pc≤b≤Δ。
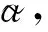
假设3假设废旧产品的供应量为G(Pc)=α+βPc[11],其中α为废旧产品的市场基础,β为回收价格敏感系数。
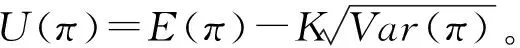
主要模型参数及描述如表1所示。

表1 主要模型参数及描述
注:i=0,1,2,3分别表示均为风险中性、均为风险规避、制造商风险规避且零售商风险中性、制造商风险中性且零售商风险规避4种情形;j=m,r,分别代表制造商和零售商
2 模型求解与分析
2.1 成员风险中性下的模型建立
为便于比较分析,首先考虑双方均为风险中性的情况。制造商作为Stackelberg博弈的主导方,零售商为跟随方。博弈顺序为:制造商先制定产品的批发价格W、网上直销渠道价格Pd和回收转移费用b,零售商后决策零售价格Pr和废旧品的单位回收价格Pc。双方均以自身利益最大化为目标进行决策,由于双方均为风险中性,因此效用函数即为期望利润函数,则有:
(Δ-b)(α+βPc)
(1)
(2)
通过逆向归纳法求解式(1)和式(2),可得命题1。
命题1当制造商和零售商均为风险中性时,双渠道闭环供应链的最优定价决策为:
(3)
(4)

(6)

(7)
由命题1可知,产品的批发价格W和网上直销渠道价格Pd与消费者网上直销渠道偏好θ成正比,传统零售渠道价格Pr与消费者网上直销渠道偏好θ成反比。零售商的废旧品回收价格Pc和制造商转移费用b与消费者网上直销渠道偏好θ无关。
2.2 双方风险规避下的模型建立
对于风险规避的制造商和零售商,博弈顺序与双方均为风险中性情形一致。根据均值-方差方法,制造商和零售商的效用函数分别为:
(Δ-b1)(α+βPc1)-
Km1σ[W1-Cm+(Pd1-W1)s]
(8)
(b1-Pc1)(α+βPc1)-
Kr1σ[(Pr1-W1)(1-s)]
(9)
通过逆向归纳法求解式(8)和式(9),可得命题2。
命题2当制造商和零售商均为风险规避时,双渠道闭环供应链的最优决策为:
(10)
(11)
(12)

(13)

(14)

推论1表明当制造商厌恶风险时,会减少投入成本以规避市场的不确定性,因此制定的直销价格也会较低。当零售商也为风险规避时,会减少销售努力,产品的零售价格也会随之降低。如果消费者更偏爱网络渠道,那么制造商会借机提高网上直销渠道价格,但当制造商为风险厌恶时,价格会受到其自身风险规避度的影响。对于零售商而言,零售价格会受到双方风险规避的影响。随着零售渠道的市场需求减少,面对趋于保守的制造商,零售商会采取低价策略吸引消费者,从而增加市场份额以弥补消网上直销渠道竞争造成的利润损失。
将式(11)和式(12)代入需求函数,可得到命题3。
命题3当制造商和零售商均为风险规避时,产品的需求量为:
(15)
(16)
由命题3不难得出,qd1与制造商的风险规避系数Km1成正比,与零售商的风险规避系数Kr1成反比;qr1与制造商的风险规避系数Km1成反比,与零售商的风险规避系数Kr1成正比。这是因为制造商和零售商越害怕风险,制定的直销价格和零售价格就会越低,需求量也就随之增加,市场总需求量也会增加,但同时也会受到对方风险规避的影响。
2.3 单方风险规避下的模型建立
考虑成员单方为风险规避,即制造商风险规避、零售商风险中性和制造商风险中性、零售商风险规避两种情形下的供应链最优决策。同样采用逆向归纳法求解,结果如表2所示。
根据命题1和命题2,可得推论2。
推论2三种情形下,当风险规避度一定时,满足W2 表2 风险规避度不同时的均衡解 从推论2可以看出,成员的风险规避态度影响供应链定价决策。批发价格W在制造商风险中性、零售商风险规避时最高,双方均为风险规避时次之,制造商风险规避、零售商风险中性时最低。在制造商主导的供应链中,制造商拥有绝对的主导权,但随着双方风险规避度的变化,制造商的优势地位逐渐削弱,而零售商的议价能力逐渐提高。零售价格的变动则与现实的零售市场一致,批发价格越高,零售价格也越高。废旧品的回收价格不受成员风险规避度的影响,在三种情形下均相等。 考虑到模型中参数较多,为更好地研究风险规避度和消费者偏好对双渠道闭环供应链的影响,采用Matlab进行数值分析来检验模型的有效性。主要参数赋值:a=100,s=0.5,Cm=20,Δ=10,σ=2,α=10,β=20。 令Km和Kr在[0.1,1.0)的范围内变动,步长为0.1,θ=0.5。绘制(Km,Kr,W)和(Km,Kr,Pd)三维立体图,分别如图2和图3所示。 图2 制造商和零售商风险规避系数对批发价格的影响 图3 制造商和零售商风险规避系数对零售价格的影响 由图2和图3可知,当Kr不变时,随着Km的增大,批发价格降低;当Km不变,Kr增大时,批发价格出现缓慢增长的趋势。综合来看,批发价格受Km的影响更大。产品的零售价格随着Km和Kr的增大而降低。 令θ在[0.1,1.0]的范围内变动,步长为0.1,Km=0.5,Kr=0.5。绘制不同情形下消费者网上直销渠道偏好对制造商和零售商效用的影响图,分别如图4和图5所示。 图4 不同情形下消费者网上直销渠道偏好对制造商效用的影响 由图4可以看出,当制造商和零售商均为风险中性和单方风险规避时,制造商效用随着消费者网上直销渠道偏好θ的增大而增大;当双方均为风险规避时,制造商效用随着θ的增大而减小。但综合来看,双方风险规避时的效用大于风险中性或单方风险规避时的效用。这说明适当的风险规避可以为供应链整体带来一定的利润。由图5可以看出,不同情形下零售商效用都是随消费者网上直销渠道偏好θ的增大而减小,这说明消费者对网上直销渠道偏好的增加势必会影响传统零售渠道的销量,从而影响零售商的利益。 考虑风险规避行为和消费者网上直销渠道偏好的双重因素,研究了3种风险态度下的最优决策问题。结果表明:①网上直销渠道价格和零售价格随制造商和零售商风险规避度的增大而降低;②当制造商和零售商均为风险规避时,效用随消费者网上直销渠道偏好的增加而降低,当双方均为风险中性或单方风险规避时,制造商效用随消费者网上直销渠道偏好的增加而增加,零售商效用随消费者网上直销渠道偏好的增加而降低,且双方风险规避时的效用大于双方风险中性或单方风险规避时的效用。
3 数值分析
3.1 风险规避度对产品定价的影响
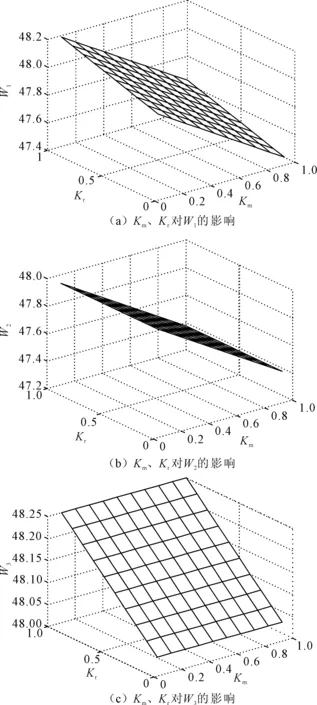

3.2 消费者网上直销渠道偏好对制造商和零售商效用的影响

4 结论
