融合模糊神经网络与时序模型的火灾预警算法
2020-06-12黄翰鹏李柏林罗建桥
黄翰鹏,李柏林,欧 阳,程 洋,罗建桥
(西南交通大学 机械工程学院,四川 成都 610031)
0 引 言
传统的火灾探测器大多以气体浓度、烟雾浓度、温度等单一的火灾特征参数作为火灾判断依据,极易受到外界干扰而导致误报以及预警不及时。近年来,研究者搭建了几种火灾预警模型,如基于BP神经网络、基于模糊神经网络、基于D-S证据理论以及相关改进算法等。段锁林等[1]以火灾火焰的温度、烟雾、辐射特征值为研究对象,提出了一种基于粒子群-小波神经网络火灾预警算法。丘启敏等[2]提出利用BP神经网络进行多传感器数据的融合,用于火灾预警,但收敛速度较慢。段锁林等[3]将模糊集合和D-S证据理论相结合,克服了火灾检测中单个传感器的不稳定性和不确定性。Chang等[4]利用模糊神经网络(FNN)算法建立火灾检测模型,但其存在易陷入局部最小值的不足。
上述算法均是对多组独立特征参数数据点进行火灾预警建模,虽取得了不错的实验效果,但没有考虑数据点之间的时序变化规律,因此对火灾预警的时效性和准确率仍有待提高。
本文为了提高现有火灾预警算法在时效性和准确率方面中的不足,提出了融合模糊神经网络(FNN)模型与温度时序模型(TSM)的火灾预警算法(FNN-TSM),通过TSM建立了数据点之间变化率的相关性,提高了在不敏感特征参数变化下火灾预警的能力,实现了更高的预警准确率。
1 FNN-TSM算法
1.1 FNN-TSM的结构设计
传统的FNN输入瞬时火灾特征参数,通过建立神经网络和模糊规则,训练得到数据点的孤立火灾概率。本文在传统FNN模型的基础上引入TSM,探测火情中温度特征参数的变化情况,监控管廊内部环境的时序火灾概率,最后通过复合决策判断火灾。本文的FNN-TSM火灾预警采用并联结构,如图1所示。主要分为3个部分:①通过FNN得到数据点的孤立火灾概率。首先归一化3个特征参数:一氧化碳(CO)浓度、烟雾浓度(S)和温度(T),然后将其输入所构建的FNN,得到孤立火灾概率。②通过TSM监控温度变化率,得到时序火灾概率。首先计算归一化后的温度时序变化率,然后将时序变化率细分为多个变化率区间,最后通过TSM输出时序火灾概率。③复合决策。加权融合孤立火灾概率和时序火灾概率,得到最终的火灾概率,输入决策层进行火灾判断。

图1 FNN-TSM火灾预警结构
1.2 火灾特征参数归一化
由于CO浓度传感器、烟雾浓度传感器以及温度传感器输出的参数数值量纲和范围都不同,同组数据数值差距较大,故为了合理利用和评价这3个特征变量,对其进行归一化处理。归一化公式为
(1)
其中,Xi表示当前输入数据,Xmin为整组数据中的最小值,Xmax为整组数据中的最大值,X′为归一化后的数值。
1.3 FNN的结构设计
本文将火灾特征参数CO浓度、烟雾浓度(S)和温度(T)作为FNN的输入,受钱伟等[5]的启发,构建7层结构的模型,包括输入层、线性变换层、模糊化层、模糊规则层、归一化层、去模糊化层和反模糊化层,如图2所示。其中:W1、W2、W3和W4分别表示(1,2)层、(2,3)层、(3,4)层和(5,6)层之间的连接权值,W、X、Z和D分别表示模糊推理中的“无火”、“小火”、“中火”和“大火”,“F”、“S”和“N”分别表示“明火”、“阴燃火”和“无火”,“P”表示图1中的孤立火灾概率。
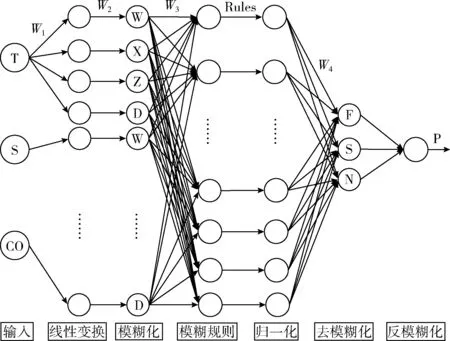
图2 FNN结构
1.4 隶属度函数与模糊推理规则
模糊化层主要是对经过线性变换层归一化后的数据进行模糊化处理,即利用隶属度函数将具体的输入量以“W(无火)”、“X(小火)”、“Z(中火)”和“D(大火)”来表示。在模糊化过程中,隶属度函数的选取直接影响着模型的输出,根据本文模型的需求,“W”、“X”、“Z”和“D”的隶属度函数均采用高斯函数,函数输出范围为0~1,高斯函数的表达式如下式所示
(2)
其中:W1和W2表示连接权值。
图2中第4层和第5层之间为模糊规则层,用来实现模糊规则的制定,由于输入层具有3个特征参数,且每个参数具有“W”、“X”、“Z”和“D”4种状态,因此模糊规则应该有4×4×4=43=64条规则,部分规则见表1。

表1 部分模糊规则示例
此外,神经网络各层单元的计算与文献[5]类似,因其不是本文研究的核心内容,不在此赘述,读者可参考该文献查看具体细节。
1.5 TSM的设计
针对火灾预警中的误报问题,龚利英[6]在决策层融合中引入烟雾持续函数,通过监测时序烟雾浓度判断火灾环境,取得了不错的效果。受此启发,本文以时序数据的温度变化率为对象进行建模,并以烟雾及CO浓度变化率的持续时间函数进行约束,提出TSM模型,计算时序火灾概率。具体步骤如下:
(1)计算传感器各时刻的数值变化率
Ki=(Ti-Ti-1)/Ti-1,i=2,…,Num
(3)
Li=(COi-COi-1)/COi-1,i=2,…,Num
(4)
Mi=(Si-Si-1)/Si-1,i=2,…,Num
(5)
其中,Ki表示i时刻的温度变化率,Li表示i时刻的CO浓度变化率,Mi表示i时刻的烟雾浓度变化率,K1=L1=M1=0;Ti为i时刻的温度值,COi为i时刻的CO浓度值,Si为i时刻的烟雾浓度值;Num为温度时序样本总数。
(2)计算CO浓度变化率持续时间函数d1(i)和烟雾梯度持续时间函数d2(i)
d1(i)=[d1(i-1)+1]u[Li-Ld],i=2,…,Num
(6)
d2(i)=[d2(i-1)+1]u[Mi-Md],i=2,…,Num
(7)
其中,u(x)为单位阶跃函数,如式(8)所示;Ld为CO浓度变化率的判断门限;Md为烟雾浓度的判断门限;d1(1)=d2(1)=0
(8)
当Li>Ld时,d1(i)叠加;当Mi>Md时,d2(i)叠加。在本文中,若d1(i)≥2,则判断CO浓度明显上升;若d2(i)≥2,则判断烟雾浓度明显上升。
(3)建立TSM,其流程如图3所示。将温度变化率输入该模块,得到时序火灾概率。其中:温度变化率Ki的阈值为bi,从大到小分别为b1、b2、b3和b4;定义时序火灾概率等级为F,其值有大到小分别为t1、t2、t3、t4和t5。
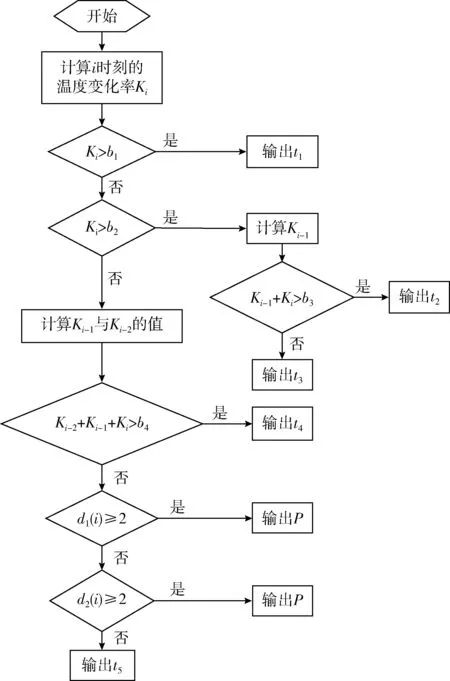
图3 TSM的流程
从图3中可以看出,本文的TSM模型建立了不同温度变化率区间下的时序火灾概率模型,通过该模型可以有效补充FNN在低特征参数环境下预警能力的不足,同时由于FNN存在一定的过拟合现象,通过该TSM可以纠正由孤立火灾概率引起的误报现象。
1.6 孤立火灾概率与时序火灾概率的融合决策
本文将FNN输出的孤立火灾概率Pi和TSM输出的时序火灾概率ti进行加权融合,得到最终的火灾概率输出,如下所示
ηi=λ1Pi+λ2ti
(9)
(10)
其中,λ1和λ2分别为孤立火灾概率和时序火灾概率的权值;ηi为i时刻管廊中最终的火灾概率。
t5为误报纠错项,用于当火灾特征参数变化未到达火灾要求时,纠正FNN中出现的误判,其计算如式(11)所示
(11)
本文算法通过采集温度传感器监测的时序数据,计算温度的变化率,通过所提出的TSM模型,综合监测管廊环境的变化情况。若温度变化率过大且达到火灾明火条件下的阈值时,将通过时序火灾概率来提高最终输出的火灾概率;若温度变化率较小且低于火灾明火条件时,可通过加大时间跨度来进行判断,在环境发生阴燃火趋势时,能够及时发现。
1.7 火灾的决策判断
本文参考金杉等[7]提出的决策方式,步骤如下:
(1)计算火灾概率相对差值Ji
(12)
其中,Rw为无火概率的稳态值。假设n个时刻的稳态值分别为xi,其稳态值的估计值为
(13)
(2)火灾判断。当Ji≥σ时,判断为火灾发生并发出警报。本文取σ的值为1.5。
2 实验结果与分析
为评估文本算法对火灾的预警能力,首先建立火灾数据的训练集和测试集,实验数据采用文献中提供的无火、阴燃火和明火数据各200组[8-10],并按火灾发生前后时序排列,部分实验数据见表2。随机抽取无火、阴燃火和明火数据各100组作为训练集,其余数据作为测试集。实验PC处理器为Inter(R) Core(TM) i7-4710HQ CPU @2.50 GHz,内存8.00 GB,在Matlab2016环境下进行实验。模糊神经网络模型直接采用MATLAB内置的模糊神经网络工具箱ANFISEDIT。
2.1 模型性能评估指标
召回率(recall)、精确率(precision)和准确率(accuracy)是评价分类或检测性能的常用指标,分别定义为
recall=TP/(TP+FN)
(14)
precision=TP/(TP+FP)
(15)
accuracy=(TP+TN)/(TP+FP+TN+FN)
(16)
其中,TP为判断为火灾的样本中,判断正确的数目;FP为判断为火灾的样本中,判断错误即误报的数目;TN为判断为非火灾的样本中,判断正确的数目;FN为判断为非火灾的样本中,判断错误即漏报的数目。需要注意的是,本文将阴燃火归为火灾类别中。
2.2 FNN结构的有效性评估
首先评价FNN结构的有效性,采用训练集中的300组数据进行训练,结果如图4所示(因空间限制,仅展示30组训练结果)。模型的训练误差设置为0.005,最大迭代次数为5000。
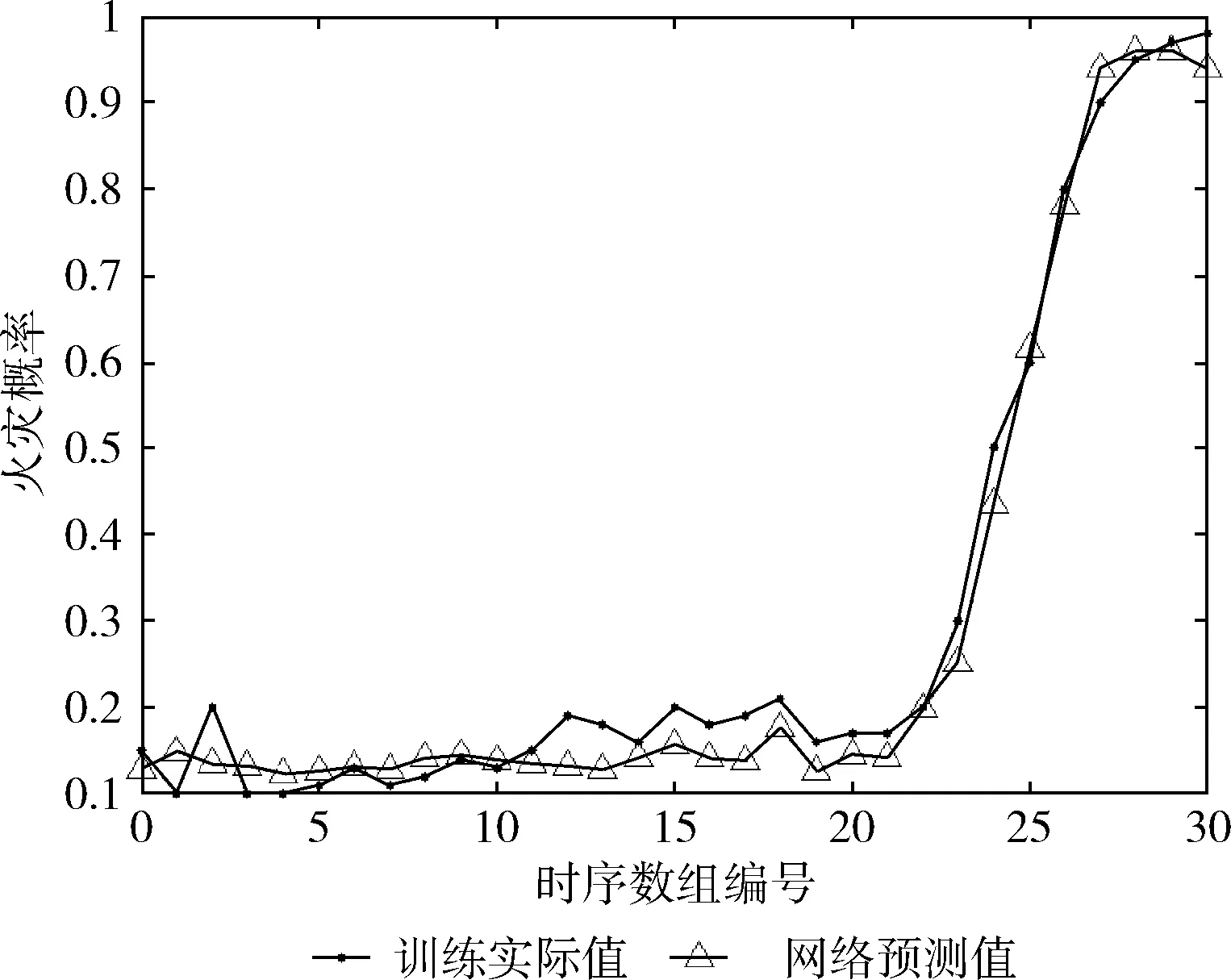
图4 FNN的训练结果
从图4中可以看出,本文建立的FNN结构对于火灾数据的训练是有效的,可以用此模型预测火灾预警中的孤立火灾概率。
2.3 TSM模型的参数选择
本文算法中所需要设定的参数包括温度变化率阈值bi、CO浓度变化率判断门限Ld、烟雾浓度判断门限Md、无火概率稳态估计值Rw(n)、TSM的输出概率ti以及权值λi。
(1)bi、Ld和Md的确定。阈值bi、门限值Ld和Md直接影响TSM的输出ti,具体取值可根据火灾中无火、阴燃火和明火的实际情况综合分析。本文采用文献中使用的火灾模拟软件FDS[11,12],模拟管廊中的火灾数据曲线,参照火灾发生前后特征参数浓度随时间的变化情况,具体取值分别为b1=0.4,b2=0.3,b3=0.2,b4=0.1,Ld=0.15,Md=0.15。
(2)ti的确定。统计火灾模拟实验数据[11-14],分析火灾数据中温度的变化曲线,结合多种火灾发生前中后期温度的变化情况,得出经验值t1=3.3,t2=1.3,t3=0.5,t4=0.1。
(3)Rw(n)的确定。本文采用300组训练数据集中的无火训练组作为计算数据计算无火概率稳态值的估计值,得到Rw=0.125。
(4)λi的确定。为确定权值λ1和λ2的值,本文选取λ1为实验对象,分别将λ1设置为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1进行火灾判断实验,实验数据及设置与前文相同,其实验结果如图5所示。
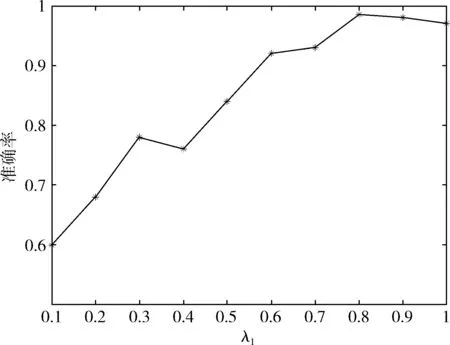
图5 不同权值下的火灾判断准确率
从图5中可以看出,当权值λ1较小即权值λ2较大时,本文算法中的TSM对管廊的大环境产生错误解读,导致误报率较高;当权值λ1过大即权值λ2过小时,TSM在预警过程中起到的作用被削弱,导致火灾预警的能力下降。特别地,当权值λ1的取值为0.8时,本文算法取得最高的火灾判断正确率,为98.67%。综上所述,本文选取权值λ1=0.8,λ2=0.2。
2.4 结果分析
(1)与传统FNN的对比。首先,验证本文所提出的FNN-TSM方法中TSM在火灾预警中的有效性。因空间限制,选取其中60组测试数据的实验结果进行展示,如图6所示(为给读者展示实验结果的细节,分3个子图显示)。

图6 不同数据组下的火灾预测概率
从图6(a)和图6(c)中可以看出,在无火阶段, FNN-TSM的火灾概率预测值基本与FNN的预测值一致,即保持了传统FNN对无火特征参数的良好预测性能;从无火进入有火阶段,FNN-TSM对同一时序数据的火灾概率预测值明显高于FNN的预测值,这是由于TSM能够监测火灾特征参数的大环境,通过监测温度的变化率合理调整火灾概率的预测值,由此得出FNN-TSM对无火到有火这一阶段的感知更加敏感,能够实现对火灾判断的实时性。
从图6(b)中可以看出,本文所提出的FNN-TSM通过融合TSM能够纠正由FNN引起的误报(如对第4组和第7组的预测结果所示),提高了火灾预警的正确率。这是由于在FNN-TSM的TSM中,通过引入CO和烟雾浓度变化率持续时间函数对时序火灾概率进行辅助判断,克服了FNN对孤立数据火灾概率的错误感知,较好解决了无火阶段的误报。
(2)与其它几种火灾预警方法对比。为综合评估本文FNN-TSM算法对火灾的预警能力,对文献[2,6,8]中的几种方法进行了对比实验,实验结果见表3。加粗表示最好结果。
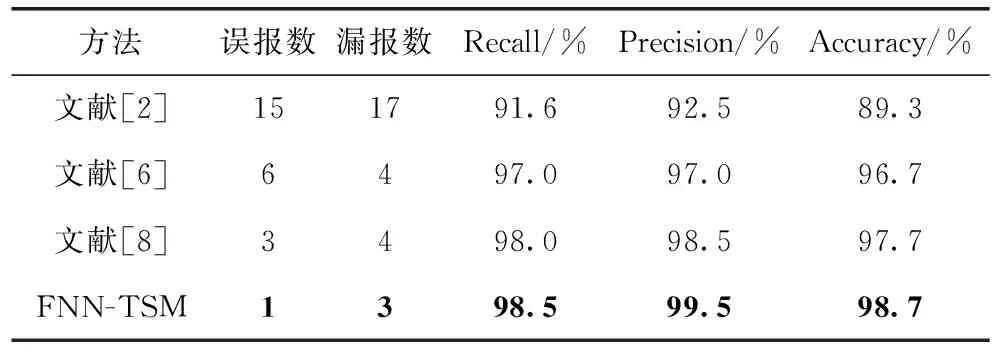
表3 实验结果对比
从表3的实验结果可以看出,文献[2]的准确率最低,为89.3%,其主要原因是其采用BP神经网络对火灾特征参数进行建模,以单一的火灾输出概率进行火情判断,可靠性较低。文献[6]在BP神经网络的基础上引入了模糊逻辑,并采用L-BFGS算法对BP神经网络的收敛速度和精度进行了优化,提高了火灾预警的正确率,达到了96.7%,但缺乏决策层。文献[8]在RBF神经网络的基础上融入了模糊逻辑,划分神经网络的输出值区间,并以模糊逻辑的输出值对神经网络的输出值进行二次模糊,决策判断火情,正确率达到了97.7%。本文提出的FNN-TSM取得了最佳的准确率值,为98.7%。原因为:本文通过建立以温度、CO浓度和烟雾浓度为火灾特征参数的FNN模型,得到监测数据的孤立火灾概率;通过建立温度特征参数的变化率模型,并以CO和烟雾浓度变化率持续时间函数进行辅助判断,综合监测管廊环境的变化情况,得到时序火灾概率。然后,加权融合孤立火灾概率和时序火灾概率得到最终的模型概率输出。最后,以提出的决策方式来判断当前火情。综上分析,本文不再以单一模型的输出值作为火灾的判断依据,提高了火灾判断的可靠性与实时性,预警能力对比如图7所示。
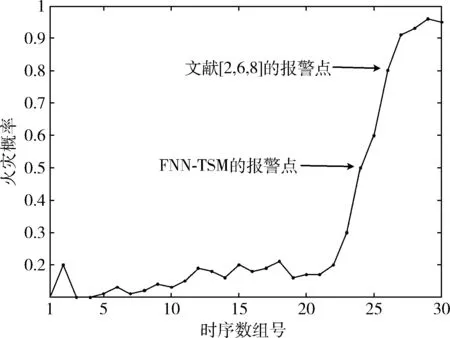
图7 火灾预警能力对比
3 结束语
综合管廊的火灾探测与预警是一个难以用精确数学模型描述的问题,本文以温度、烟雾浓度和一氧化碳浓度3种火灾特征参数为研究对象,提出FNN-TSM模型。该模型首先建立以孤立数据点为输入的FNN,建模孤立火灾概率;然后以TSM综合感知管廊环境的时序变化情况,获知时序火灾概率;最后采用加权融合得到最终的火灾概率,并提出决策方式来判断火情。实验结果表明,本文算法与文献中的几种方法相比,不仅提高了火灾判断的正确率,而且预警的时效性也得到了较大的提高。
