基于属性加权k最近邻算法的降雨预测

周 芸，杜景林，陶 晔

(南京信息工程大学 电子与信息工程学院，江苏 南京 210044)

0 引 言

由于降水天气成因复杂且形势多变，传统降水预报方法的准确度难以满足人民的需求[1,2]。近年，越来越多的数据挖掘与人工智能技术被应用于降水预报领域，并表现出比传统降水预报方法更好的性能[3]。Du J等[4]为提高模型的性能，提出基于粒子群算法优化支持向量机参数(PSO-SVM)的降水预报模型。Huang M等[5]提出一种基于距离加权的k最近邻算法，并将该算法用于降水等级预报与晴雨预报，改进后的方法具有较好的预报效果。Haidar A等[6]将遗传算法与前馈神经网络相结合，首先利用遗传算法选择合适的预报因子，然后应用前馈神经网络构建降水预报模型，对澳大利亚东部地区的月平均降水进行预报。然而这些方法在搭建降水预报模型时都未曾考虑不同气象因子对降水量的影响程度存在相异性。针对上述问题，本文提出一种基于属性加权的k最近邻算法，通过各属性上不同类别的数据分布情况，计算各属性的权值，并将此算法用于南京地面观测站的降水预报。本文建立的降水预报模型在准确率、TS评分等降水预测评价指标上均有所提高和完善。

1 背景知识

1.1 KNN

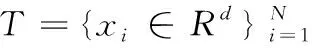
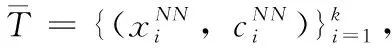
(1)

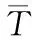
(2)

(3)

1.2 属性重要度

在自然场景下的分类问题，不同属性对分类结果的影响各不相同[8]。通常认为属性空间上的类别分布可以表示属性的重要度，属性空间上类内分布越集中，类间分布越分散，越有利于分类预测，这些属性对于分类结果的重要性也就越高[9]。

(4)

式中：wa表示属性a的权重，σai表示在属性a上类标签为Ci的属性值的标准差；i∩j表示在属性a上类标签为Cj的属性值落在类标签为Ci的属性值区间的样本个数；i∪j表示在属性a上类标签为Ci和类标签为Cj的样本个数总和；α为缩放因子，通过实验经验选取，本文将其值设置为常数0.25。

由式(4)可以看出，类内分布情况可由属性上类别的标准差σai表示，σai值越小表示该属性的类内分布越集中；类间分布情况可由属性上不同类别样本的交集与并集的比值表示，该值越小表示该属性的类间分布越分散。通过属性空间上同类数据分布的内聚性和异类数据的耦合性可以表示属性的重要度。

2 属性加权k最近邻算法

传统KNN算法在进行分类预测时，将参与分类的属性视为同等重要，即为每个属性都设置相同的权值。然而在实际应用中，不同属性对分类结果的影响各不相同。以降水预报为例，对降水预测结果造成重要影响的通常是预报因子中的一个或几个关键因子。因此在对多维数据集进行分类预测时，应当充分考虑不同属性与类别的关系紧密程度。为了区分不同属性的重要程度，本文提出一种基于属性加权的k最近邻(attribute-weighted k-nearest neighbor，AKNN)算法，该算法根据各属性对分类结果的贡献，赋予不同属性不同的权值。

步骤1 计算出属性的权重矩阵Wa=(wa1wa2…wad)，其中wa1、wa2…wad分别代表每个属性的对应权重，由式(4)计算得到。

(5)

式中：符号∘代表哈达玛乘积。

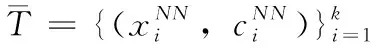
(6)

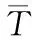
(7)

由AKNN算法的步骤1与步骤2可知，不同于传统KNN算法没有考虑各属性对分类结果的影响各不相同，AKNN算法根据不同属性对分类结果的影响程度计算属性的权值，并通过属性加权的方法削减不重要属性对分类结果的影响。

3 基于属性加权k最近邻算法的降水预报

3.1 资 料

实验数据来源于中国气象数据网(http://data.cma.cn/)提供的2015～2018年6月～8月南京地面观测站点的观测资料。根据降水量的大小，将资料中的样本分为无雨、小雨、中雨、大雨与暴雨5类，并将它们相应标记为{0,1,2,3,4}。考虑到气象部门的降雨量等级划分标准多按12 h或24 h计算，本文采用防汛部门的1 h降雨量等级划分方法对样本的降雨量进行划分，具体划分标准见表1。

表1 1 h降水量等级划分

考虑各属性与降水量的相关性，本文选择大气压强(百帕)、风向(度)、风速(米/秒)、气温(摄氏度)、相对湿度(百分率)作为降水分类预测的样本属性[10]。不同气象要素往往具有不同的量纲和量纲单位，为了消除气象要素之间的量级差异，需要把不同气象要素的数据统一到同一数量级，即对样本数据进行归一化处理。归一化公式如式(8)所示

(8)

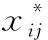
3.2 基于属性加权k最近邻算法的降水预报模型

应用AKNN算法构建的南京地面观测站点的降水量预报模型可表述如下：

(9)

另外，给出待预报的样本xt如式(10)所示

xt=xt1xt2xt3xt4xt5

(10)

式中：xtj表示待预报的样本xt的第j个气象属性值。

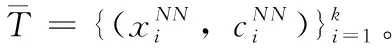
4 实验结果与分析

为了验证本文提出的降水预报模型的效果，首先采用10-折交叉验证方法将数据集划分训练样本与测试样本，然后根据第3节所述步骤分别进行降水量等级预报实验与晴雨预报实验。本实验采用python语言编程实现，硬件环境为Inter(R) Core(TM) i5-3470 CPU 3.20 GHz。

在降水量等级预报实验中，为了验证基于AKNN算法的降水预报模型的先进性，将本文方法与其它降水预报模型进行比较。参与实验的其它模型分别是基于KNN算法的降水预报模型与基于距离加权k最近邻(distance-weighted k-nearest neighbor，WKNN)算法的降水预报模型。显然，分类算法是3种降水预报模型的唯一区别，即模型的最终预测性能取决于分类算法的显著性。因此选择准确率作为评估模型性能和预测精度的指标，具体公式如式(11)所示

(11)

由于实验资料中类标签为4(暴雨)的样本个数较少，参数k取值从1～5，测试3种降水预报模型的预报准确率，得到的结果见表2。由表2可以看出：在参数k取值相同的情况下，本文提出的基于AKNN算法的降水预报方法的准确率高于其它两种降水预报方法；算法相同的条件下，k值与降水预报的准确率基本成正相关；从总体趋势显示，与KNN算法和WKNN算法相比，AKNN算法进一步降低了分类性能对参数k的依赖性。

固定参数k的数值为3，计算上述3种降水预报模型在每类样本上的预报标准误差，得到结果如图1所示。由图1可以看出：由于各类样本在实验资料中所占比重的不同，3种算法对降水等级为无雨和小雨的样本同时表现出较好的性能，而对降雨量大的样本表现的性能都较差；针对降水量大的样本(降水等级为大雨或暴雨)，基于AKNN算法的降水等级预报模型的性能优于其它两种模型。

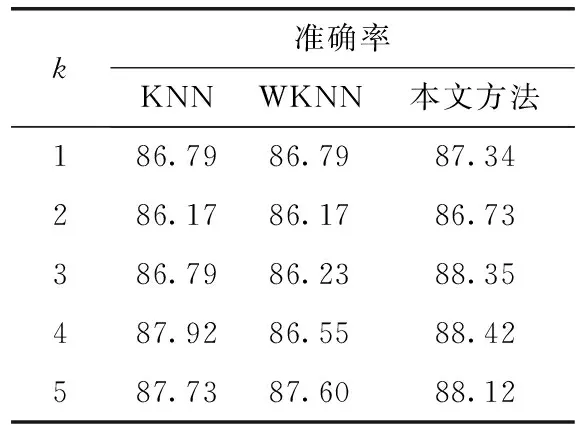
表2 3种降水量预报方法的预报准确率对比

图1 3种模型的降水预报标准误差

为了进一步检验降水预报模型的性能，分别利用上述3种降水预报模型对实验资料进行晴雨预报。本文采用文献[11]的建议，使用准确率、TS评分、正样本概括率(SAR)和漏报率(MAR)作为晴雨预报的性能评价指标。其中准确率的计算方法见式(11)，TS评分、正样本概括率和漏报率的计算方法分别见式(12)、式(13)和式(14)

(12)

(13)

(14)

hits、misses、false、correct的含义见表3。

表3 模型预报与观测列联表

根据参考文献[12]和实验资料中类标签为4(暴雨)的样本数目，参数k取值从1～12，测试3种降水预报模型的性能，得到的晴雨预报效果如图2-图5所示。图2、图3、图4和图5分别显示了基于KNN算法、基WKNN算法和基于AKNN算法3种晴雨预报方法在不同k值情况下的准确率变化、TS评分变化、正样本概括率变化和漏报率变化。在晴雨预报中，准确率、TS评分和正样本概括率的数值越高说明模型对降水情况的预测性能越好。从图2-图4可以看出，本文提出的晴雨预报方法，在准确率、TS评分和正样本概括率上总是优于另外两种晴雨预报方法。也就是说，基于AKNN算法的晴雨预报不仅在总体上具有更好的分类精度而且对有雨的情况具有更好的预测性能。此外，在晴雨预报中，模型的漏报率越小说明模型的预测性能越好。从图5可以看出，在参数k取值相同的情况下，本文提出的模型可以更好地减少有雨类样本的漏报。以k=5为例，基于KNN算法的降水模型的漏报率为30.74%，而基于本文算法的降水模型的漏报率为22.65%，比前者降低了8.09%。

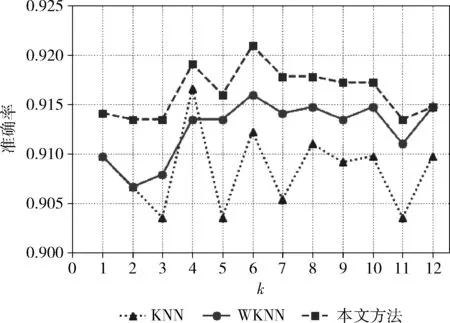
图2 3种预报方法的准确率对比

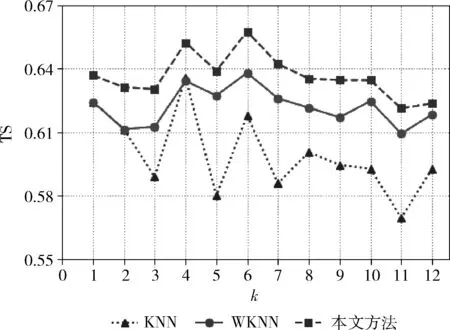
图3 3种预报方法的TS评分对比

图4 3种预报方法的正样本概括率评分对比

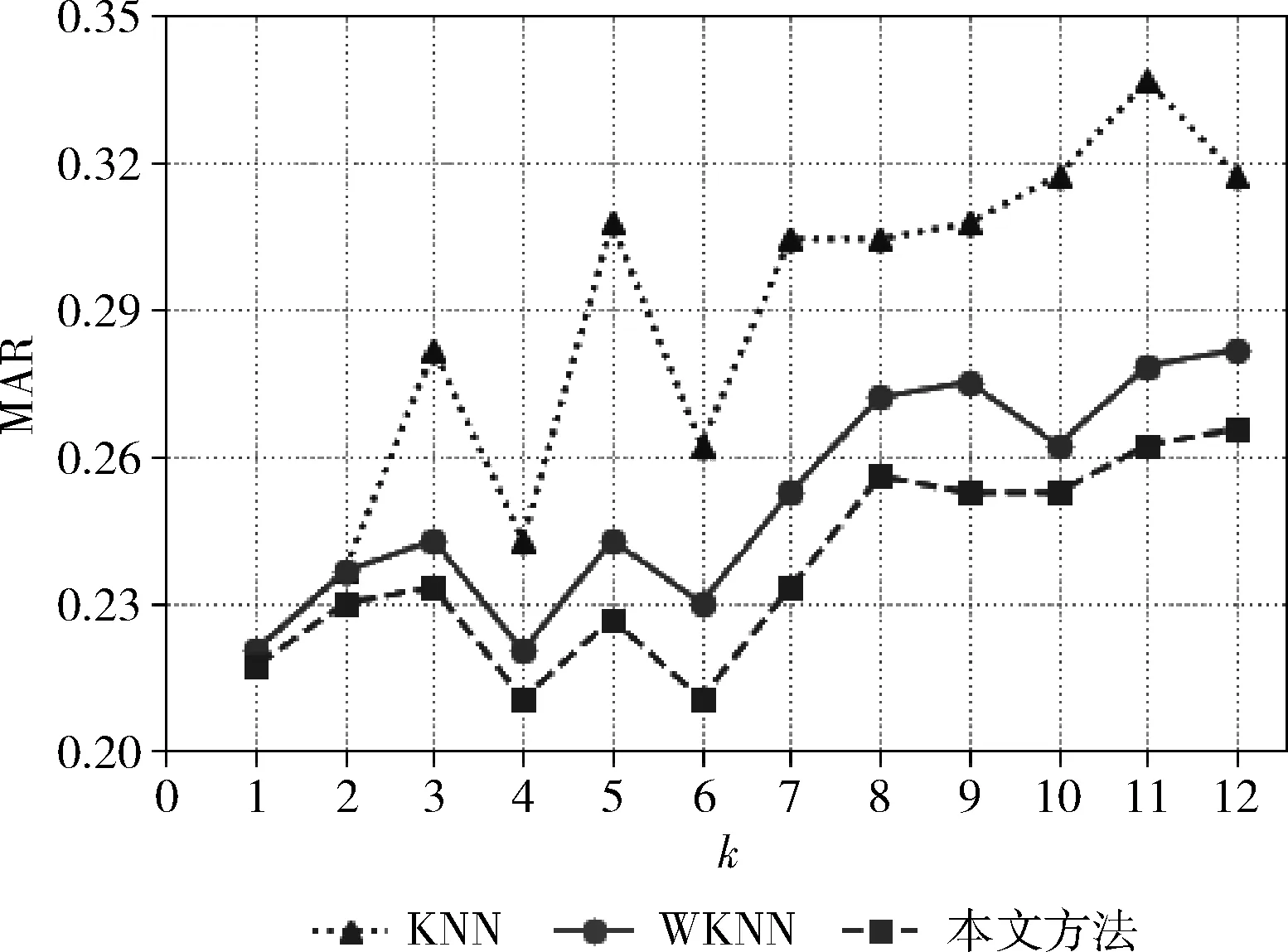
图5 3种预报方法的漏报率对比

5 结束语

本文首先提出一种改进的k最近邻算法，该算法通过属性加权的方式提高重要属性对分类结果的影响，可以有效降低算法对参数k的依赖性。然后在改进k最近邻算法的基础上，提出了一种降水预报方法。实验结果表明，基于AKNN算法的降水预报方法的总体预报效果较好，并在一定程度上提高了大降雨量样本的预测精度。然而针对降雨量大的天气，模型的表现性能仍较差。因此，下一步拟考虑将本文改进的k最近邻算法与类别子空间的思想相结合，以进一步提高降水量等级预报的预测精度。